基于模块化多电平换流器的多端柔性直流输电系统自适应电压下垂控制

孙 季，邱建龙*，刘学强，赵浩东，陈向勇

（1.临沂大学 自动化与电气工程学院，山东 临沂 276005；2.国网山东电力公司 临沂供电公司，山东 临沂 276001）

近年来，可再生能源基地通过基于电压源换流器的柔性直流输电系统（voltage source converterhigh voltage direct current，VSC-HVDC）向大负荷中心供电逐渐成为人们关注的焦点[1]，其中，研究HVDC 系统的保护[2]和控制[3]等问题是当前比较活跃领域。现有的柔性直流工程大多是点对点的HVDC，随着可再生能源发电量和装机容量不断提高，多端柔性直流输电技术（multi-terminal direct current，MTDC）能够同时将多个可再生能源发电站连接到多个负载中心[4]，并且可以提高电力系统的可靠性和稳定性[5]，是一种解决新能源电站大规模电力输送难题的有效的技术手段[6]。模块化多电平换流器（modular multilevel converter，MMC）是目前在世界范围内引起广泛研究和开发的电压源换流器（voltage source converter，VSC）拓扑之一，由于子模块内部的特殊构造，避免了开关器件（insulated gate bipolar transistor，IGBT）的直接串联，制造难度下降，易于在工程上实现。此外，MMC 还具有损耗低、阶跃电压低、波形质量高、故障处理能力强等优点，是现阶段多端柔性直流输电系统换流器的主流选择。

与交流系统中频率相对应，直流电压是MTDC系统中功率平衡和稳定运行的指标，在系统整体设计中处于重要地位。当前控制MTDC 直流电压的基本方法主要有主从控制、电压裕度控制和电压下垂控制。主从控制[7]虽然直流电压控制精度高，但是需要快速通信，而且如果主站发生故障退出运行，则整个MTDC 失去直流电压控制能力、可靠性较差；电压裕度控制必须考虑各换流站参考直流电压之间的裕度，否则可能会引起系统振荡[8]；电压下垂控制[9]无需通信，使所有采用电压下垂控制策略的换流器都能同时参与直流电压调节并且共享不平衡功率，比主从控制具有更高的可靠性且不会产生与电压裕度控制类似的系统振荡。

然而，下垂系数固定的传统电压下垂控制仍有一些缺陷，如在系统发生大的扰动时，直流电压可能会超出稳定安全运行的界限，或者换流站过载等[10]。为了解决这些问题，文献[11]使用扰动方法开发下垂控制策略，以提高控制性能，避免功率变化情况下功率转换器的负担。文献[12]考虑不同换流器的功率裕度，确定了各下垂系数的比值关系，使功率裕度更大的换流器能够承担更多的功率分配任务，避免换流器发生过载情况。文献[13]提出一种应用于大规模新能源并网的多端柔性直流输电系统双因子自适应下垂控制策略，使每个受端换流站下垂曲线根据最优功率分配原则发生自适应偏移。文献[14]研究了一种MTDC 的直流电压自适应下垂控制策略，可以在任何换流器退出运行或功率不平衡期间，确保其余换流器不会过载。文献[15]提出了一种自适应下垂控制方法，该方法根据可变下垂常数来保持有功功率共享的平衡，并在大的功率扰动中控制直流电压的变化。文献[16]提出了一种基于自适应下垂系数的改进协同控制策略，以实现更快的动态响应和更合理的功率分配，并且增加了功率和电压偏差控制，以防止输出功率和直流电压超出换流器可以承受的范围。文献[17]引入了与交流系统中频率抑制储备类似的过电压和欠电压抑制储备的概念，提出了一种确定换流器下垂设置的方法，以确保并增强MTDC 系统中的电压调节能力。文献[18]结合电压裕度控制方法和自适应下垂控制方法，提出了一种直流电压裕度的自适应下垂控制策略，可以根据不同的工况调整对应的控制模式。文献[19]将P/V 下垂控制和I/V 下垂控制相结合，提出了一种用于MTDC 的稳态功率分布推导方法，可以实现MTDC 系统和直流网络中功率和电流的共同调节。

本文重新确定了采用下垂控制的换流器直流电压和有功功率之间的耦合关系，同时结合各换流器测量的有功功率，确定了下垂系数的形式，设计出一种新的直流电压自适应下垂控制器。与现有的下垂控制策略相比，本文所提出的下垂控制策略以固定系数的非线性下垂控制为基础，具有更好的直流电压控制能力，同时根据换流站的本地电气量自适应调节下垂系数，可以有效地处理换流站过载问题。

1 MTDC 系统结构与建模

1.1 MTDC 系统拓扑结构

典型的MTDC 系统拓扑结构有星型结构（如南澳三端柔性直流工程）、环形结构（如张北柔性直流电网工程）[20]。本节以连接风电场和交流电网的MTDC 星型结构为例，如图1 所示，介绍MTDC系统的基本运行方式。风电场连接的换流站将风电机组产生的交流电整流成直流电，再经过输电线路（电缆或者架空线）将电能输送给各个交流电网连接的换流站，随后逆变为交流电输入交流电网。整个系统的布局、输电线路和换流站的类型视具体情况而定。

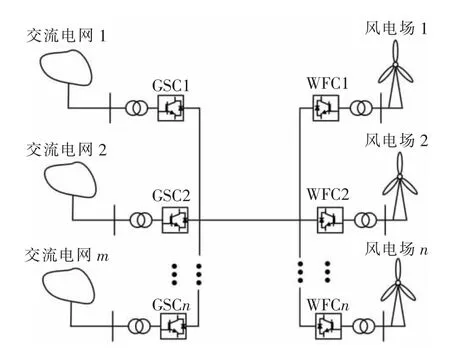
图1 连接风电场和交流电网的MTDC 系统拓扑结构[1]Fig.1 Topology of MTDC system connecting wind farms and AC grids[1]

1.2 MMC 的结构

MMC 的详细电路拓扑结构如图2 所示。换流器由3 个相单元组成，每个相单元分为上下两个桥臂，每个桥臂包含了1 个桥臂电抗器和N 个串联的子模块。子模块可采用半桥、全桥或者其他结构，每个半桥子模块包含2 个全控型开关器件——绝缘栅双极晶体管（IGBT）、2 个二极管和1 个电容器。当MMC 运行时，每个相单元的上下桥臂共投入N 个子模块，即该相单元子模块总数（2N）的一半，输出的电平数能达到N+1。

图2 模块化多电平换流器拓扑[2]Fig.2 Topology of modular multilevel converter[2]

对j 相（j=a，b，c），根据基尔霍夫电压定律，可以获得MMC 的微分方程数学模型为

其中：up和un是换流器直流侧母线电压；uvj是MMC交流侧相电压；upj和unj分别是三相上下桥臂电压（不包含R0和L0上的电压）；ipj和inj是三相上下桥臂电流；R0是桥臂等效电阻；L0是桥臂电抗器电感值。

1.3 MMC 的戴维南等效模型

对模块化多电平换流器进行建模时，模型的精度和仿真的速度一直是人们考虑的主要问题。MMC的器件级模型将建模过程精确到每一个电气元件（如IGBT），这样虽然可以获得非常精确的模型，能反映MMC 的各种特性，但是仿真的速度十分缓慢，因此通常会对模型进行简化。

戴维南等效模型是对器件级详细模型的简化，该模型的建立共分3 步，如图3 所示。第一步，将子模块电容等效为电阻与电压源串联的支路，将开关器件（IGBT）及与其反并联的二极管（见图3（a））整体等效为一个阻值可变的电阻（见图3（b）），这两个可变电阻的阻值由MMC 的控制器决定。当开关器件T1导通、T2关断时，可变电阻R1的阻值很小（通常为毫欧级），R2的阻值很大（通常为兆欧级），此时子模块投入使用；反之将子模块从桥臂中切除。第二步，根据戴维南定理，建立单个子模块的戴维南等效模型（见图3（c））。第三步，将各个桥臂子模块戴维南等效模型分别进行代数叠加得到单个桥臂的戴维南等效模型（见图4）。

图3 子模块的戴维南等效模型Fig.3 Thévenin equivalent for a submodule

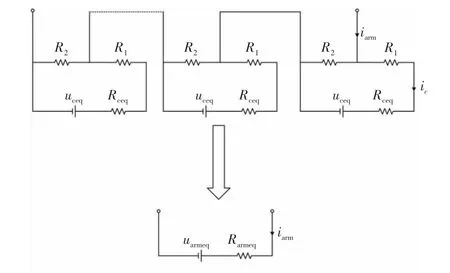
图4 单个桥臂的戴维南等效模型Fig.4 Thévenin equivalent for a single phase arm of MMC

对于一个电容元件，其伏安特性关系为

其中：uc为子模块电容电压；Csm为子模块电容值；ic为子模块电容电流。

为了便于仿真模型在计算机中解算，使用数值分析中的梯形积分法[21]，将电容的伏安特性关系离散化，取离散步长为ΔT，则离散化后电容的伏安特性方程为

电容等效电压源为

由式（5）可知，电容的等效电压源uceq（t-ΔT）由上一时刻的电容电压和电容电流求出。

电容等效电阻为

根据基尔霍夫电流定律（Kirchhoff's current law，KCL）和基尔霍夫电压定律（Kirchhoff's voltage law，KVL）可知，

其中iarm为桥臂等效电流，则子模块电容电流为

由戴维南定理得子模块的等效电阻为

子模块等效电压源为

由于整个桥臂子模块串联，故单个桥臂的等效电阻和等效电压分别为

其中：N 表示单个桥臂中所有子模块的数量；Rarmeq_k和uarmeq_k分别表示第k 个子模块的等效电阻和等效电压。

由式（3）～（12）可以看出，戴维南等效模型可以反映出每一个子模块的电容电压特性，具有较高的精度，同时离散方程便于电磁暂态仿真软件解算，具有较高的仿真速度。

2 直流电压自适应下垂控制策略

2.1 柔性直流输电系统的控制结构

控制系统对柔性直流输电系统的稳定运行至关重要，通过对换流站的控制，实现对整个柔性直流输电系统的控制。为了简化模型，且便于控制器设计，通常将三相静止坐标系下的正弦电压电流交流量经过派克变换转换为同步旋转坐标系（dq 坐标系）下的直流量，在dq 坐标系下，控制系统具有两个级联控制环，即外环控制和内环电流控制。外环控制器负责控制VSC 的直流电压和功率，同时向内环电流控制器提供电流在dq 坐标系中的参考值。内环电流控制器一方面使输出的电流dq 轴分量跟踪外环控制器提供的参考值；另一方面，抑制在换流器三相桥臂中流动的内部环流。

2.2 约束条件

对于多端柔性直流输电系统的控制而言有几个约束条件，这些约束主要考虑的是在实际应用中，换流站的运行受到一定因素的影响，为了保证系统安全和经济效益，制定如下约束条件（见图5）。

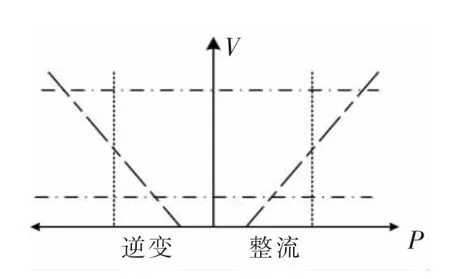
图5 P-V 平面下系统约束Fig.5 System constraints in P-V plane

1）直流电压约束有上限和下限，体现为直流电压偏差，上限由开关器件的耐压值等因素决定。下限一方面要考虑线路损耗，输送的有功功率不变时，直流电压降低会导致直流电流增大，从而输电线路的功率损耗增加；另一方面，换流器的拓扑结构（MMC 子模块数量）、调制比等也会影响电压下限值。在P-V 坐标系中，表现为两条水平直线。

2）功率约束有上限，体现为换流器容量，主要由换流器中半导体开关器件的电流限制决定，在PV 坐标系中，表现为两条竖直直线。

3）直流电流约束有上限，主要受直流电缆等直流侧的部件影响，在P-V 曲线中表现为两条斜线。

2.3 传统固定系数下垂控制

对于点对点柔性直流输电系统，通常的做法是其中一个换流站采用有功功率控制模式，以确保稳定的功率输送；另一个换流站维持直流电压，充当松弛换流站。对于具有多个换流站的MTDC 网络，在一个或多个换流站退出运行后，其他换流站应该按照一定比例分担由此产生的不平衡功率。因此其他换流站都应采用直流电压控制模式（即作为松弛换流站），而不是跟踪自身的功率参考值。然而，对所有参与功率分担的换流站设定直流电压参考值（使其运行于直流电压控制模式），需要复杂且周密的计算，而且这些直流电压参考值容易相互冲突，导致系统运行不稳定。

根据交流系统调速器控制的有功功率-频率下垂控制思想，直流电压下垂控制可以修改直流电压控制模式下的直流电压参考值，相较于主从控制策略，其牺牲一定的直流电压控制能力，让采用下垂控制的各换流站能够在整个系统功率发生波动时以适当的比例共享不平衡的功率，共同参与直流电压控制。以功率流入直流电网的方向为正方向，传统的下垂控制的有功功率-直流电压关系（P-V）为

式中：Udcref，i和Udc，i分别是第i 个换流站的直流电压参考值和实际值；Kdroop，i是第i 个换流站的下垂系数，Kdroop，i＞0，与换流站的额定容量有关；Pref，i和Pi分别是第i 个换流站的有功功率参考值和实际值。本文设置送端换流站采用恒定功率控制，受端换流站采用下垂控制，直流电压偏差不超过参考值的±5%，功率以换流器额定容量为基准值，电压以参考电压为基准值，使用标幺制设计控制器。故Udcref，i=1 pu，0.95 pu≤Udc，i≤1.05 pu，受端换流站的有功功率范围为-1 pu≤Pi≤0 pu。传统固定系数下垂控制器示意图如图6 所示。

图6 传统固定系数下垂控制框图Fig.6 Block diagram of traditional droop control with fixed coefficient

传统固定系数下垂控制的直流电压和有功功率呈线性关系，当系统功率发生较大波动或者有换流站中断时，直流电压偏差和有功功率很容易超过极限值，从而影响整个系统的安全运行，造成经济损失。这些由固定下垂控制引发的问题可以通过使用自适应下垂控制较好的解决。

2.4 自适应下垂控制

对于固定下垂控制器，下垂系数通常根据运行于下垂控制的换流站额定容量确定。然而，当系统发生大的扰动时，直流电压可能会超出约束条件范围。对于MTDC 系统来说，直流电压稳定与交流系统频率稳定具有同样重要的地位，故本文以直流电压控制性能为第一目标，兼顾有功功率分配精度。

因为固定下垂系数中直流电压和有功功率呈线性关系，所以只要在MTDC 功率输送范围内，无论系统传输功率是否接近额定值，相同的功率波动值就会引起等量的电压偏差，这就可能导致电压超出安全运行的范围。根据控制目标的需要，本文考虑线性固定下垂的缺陷和抛物线的曲线特性，重新确定下垂控制器有功功率和直流电压的耦合关系，设计非线性下垂控制器为

同时引入自适应下垂系数

式中：Rdroop，i和Sbase，i分别是第i 个换流站的自适应下垂系数和额定容量，Sbase，i=1 pu；λ 是用户自定义正常数。此时，自适应非线性下垂控制器为

该控制器示意图如图7 所示。

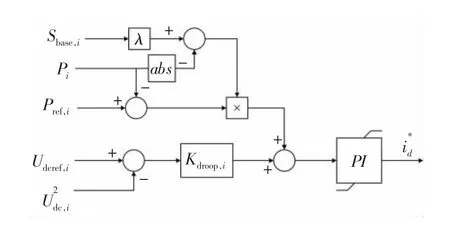
图7 本文所提出的自适应下垂控制框图Fig.7 Block diagram of adaptive droop control proposed in this paper

2.5 控制效果分析

以受端换流站GSC1 为例分析自适应下垂控制器的效果。由式（13）可得

由式（16）可得

设定换流站GSC1 的功率参考值为-0.5 pu，下垂系数Kdroop，i=20，λ=1.5，根据式（16）和（18）可得传统固定系数下垂控制和自适应下垂控制的P-V特性曲线，如图8 所示。

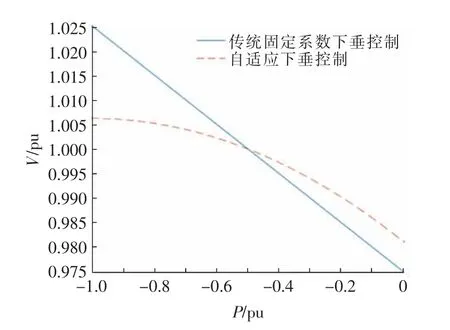
图8 两种下垂控制P-V 特性曲线对比Fig.8 Comparison of P-V characteristic curves of two droop controls

从图中可以看出，自适应下垂控制的电压偏差始终小于传统固定系数下垂控制的电压偏差，采用本文所提出下垂策略的换流站直流电压控制策略直流电压控制能力要优于传统的固定下垂控制。此外，当流经换流站的功率增大时，自适应下垂控制特性曲线的斜率绝对值也在不断减小。也就是说，当流经换流站的功率较小时，本文所提出的自适应下垂控制器更加注重功率的分配特性，即电压变化一个单位，功率变化与传统下垂控制相比较小；当流经换流站的功率较大时，功率变化一个单位，电压变化量更小，控制器侧重于电压的调节。

3 仿真验证

本节在PSCAD/EMTDC 中建立±200 kV 四端对称单极柔性直流输电系统仿真模型，以验证第2 节中讨论的自适应直流电压下垂控制策略的有效性。

如图9 所示，MTDC 系统的功能是将电力从两个海上风电场传输到两个陆上交流电网WFC1 和WFC2 是海上风电场整流器。严格来讲，WFC1 和WFC2 控制海上风电场的交流电压和频率，但是本文主要关注的是换流器直流侧电压控制及直流网络中的功率分配问题。为了简化仿真模型，同时便于模拟海上风力波动，将WFC1 和WFC2 设置为恒定功率控制模式，通过改变功率参考值模拟风力发电功率易变的特性。GSC1 和GSC2 为陆上逆变器，采用本文所提出的自适应下垂控制策略。表1 列出了此四端系统的参数。

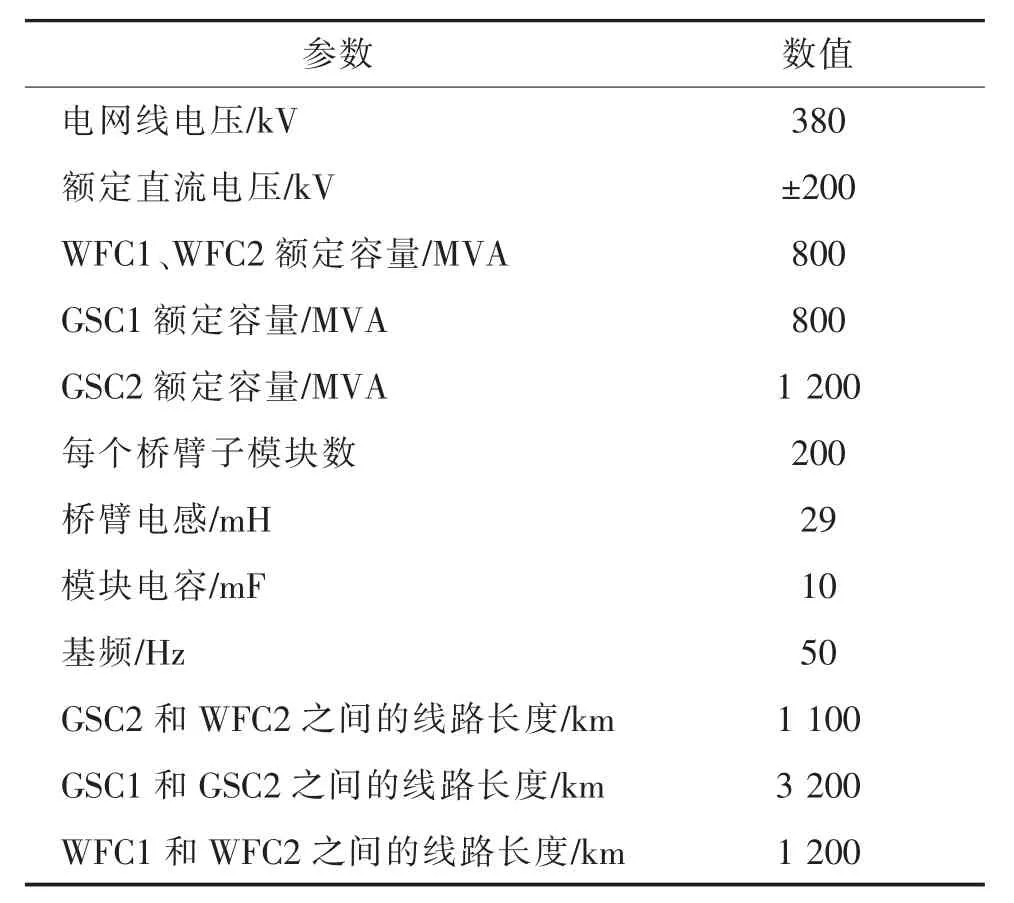
表1 MMC-MTDC 系统主要仿真参数Tab.1 Main simulation parameters of MMC-MTDC system

图9 四端柔性直流输电系统的示意图Fig.9 Diagram of the four-terminal HVDC System

换流器采用MMC 拓扑结构，以避免数百个IGBT 直接串联。为加快仿真速度，对MMC 进行戴维南等效处理。此外，采用最近电平逼近（NLM）调制方式。

3.1 稳态仿真分析

MTDC 系统的额定直流电压为400 kV，海上风电场经WFC1 和WFC2 向直流网络输送的功率各自在0～800 MW 范围内变化，测量各换流站直流母线电压、直流电流，并计算有功功率。在仿真系统中对传统固定系数下垂控制和本文所提出的自适应下垂策略进行验证，同时将本文提出的自适应下垂控制策略与文献[10]中设计的自适应下垂控制策略进行对比，以突出本文所提出的自适应下垂控制器的性能。

传统固定系数下垂控制的稳态仿真如图10 所示。在稳定状态下，WFC1 输出功率和WFC2 的输出功率皆为300 MW，此时GSC1 和GSC2 分别接收159 和425 MW 的有功功率。GSC1、GSC2、WFC1 和WFC2 的直流电压分别为393.9、395.8、402.8 和399.1 kV。由于GSC1 和GSC2 控制MTDC 系统法直流电压，且实际功率低于功率参考值，故直流电压低于电压参考值。整个系统的潮流是从WFC 传输到GSC，故WFC 电压高于GSC。送端换流站总输入功率和受端换流站总接收功率存在差异的主要原因是输电线路损耗，而各换流器传输功率及输电线路阻抗造成了各换流站直流电压并不相同。

图10 传统固定系数下垂控制稳态仿真图Fig.10 Steady state simulation diagrams of the traditional droop control with fixed coefficient

自适应下垂控制的稳态仿真如图11 所示，与传统固定下垂控制的仿真条件一致，WFC1 和WFC2 的输出功率皆为300 MW，GSC1 和GSC2 分别接收155.2 和434.8 MW 的有功功率。GSC1、GSC2、WFC1 和WFC2 的直流电压分别为395.0、397.8、404.5 和400.5 kV。以GSC1 为例，传统下垂控制直流电压偏差为6.1 kV，自适应下垂控制直流电压偏差为5.0 kV，减小了18%。与传统固定系数下垂控制相比，自适应下垂控制的电压控制效果更好；与传统下垂控制相比，GSC1 接收的功率减少了3.8 MW，GSC2 接收的功率增加了9.8 MW，容量更大、具有更多裕量的GSC2 承担了更多的功率传输任务，功率分配效果更好。

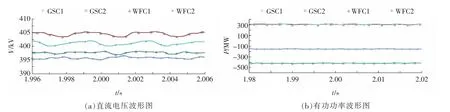
图11 自适应下垂控制稳态仿真图Fig.11 Steady state simulation diagrams of adaptive droop control

以GSC1 为例，测量不同功率输入条件下的直流电压值，仿真结果如表2 所示。

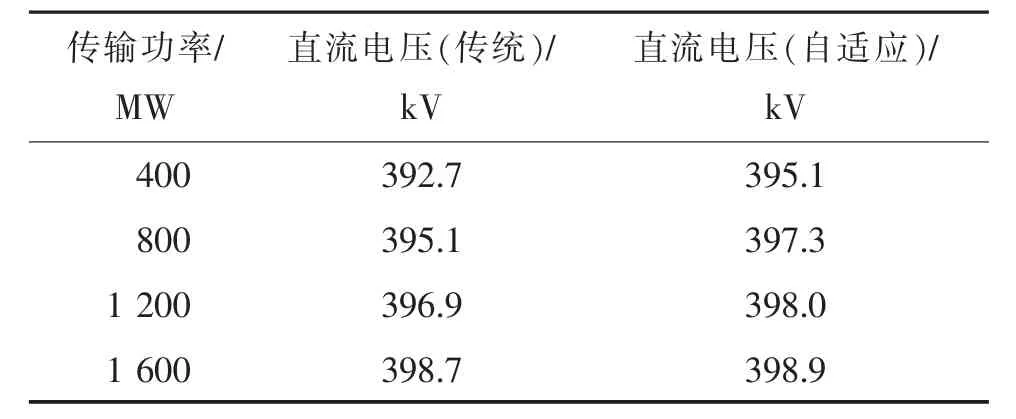
表2 GSC1 电压稳态仿真结果Tab.2 Steady state simulation results of GSC1 voltage

由表2 可以看出，当MMC-MTDC 系统采用本文提出的自适应下垂控制器时，随着MTDC 系统总传输功率在0～1 600 MW 范围内变化，直流电压的控制能力一直优于传统自适应下垂控制器。仅对自适应的直流电压而言，随着传输功率越来越多，直流电压的增加越来越缓慢。仿真结果与2.5 节控制效果分析的结论一致，验证了本文所提出自适应下垂控制的正确性。仿真结果证明，本文所提出的直流电压自适应下垂控制在稳态下能够减小直流电压偏差。

文献[10]所提出的自适应下垂控制策略和本文所提出的下垂控制策略在风电场换流器满负荷运行时的稳态仿真分别如图12、13 所示，为了便于比较，设置两种控制策略的仿真参数一致。

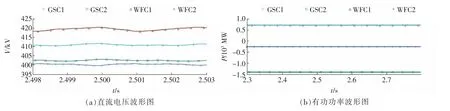
图12 文献[10]所提出的自适应下垂控制稳态仿真图Fig.12 Steadystate simulation diagrams of adaptive droop control proposed in reference[10]

由图12 所示，当WFC 满载，即WFC1 和WFC2分别向直流电网输出800 MW 有功功率时，采用文献[10]所提出的自适应下垂控制器的MTDC 系统的直流电压会超过420 kV（即直流电压参考值的5%），此时GSC1 和GSC2 分别接收189 和1 337 MW 的有功功率。由图13 可以看出，在相同的条件下，本文所提出的下垂控制策略可以将各个换流器的直流电压都限制在安全运行范围之内，此时GSC1 和GSC2 分别接收269 和1 252 MW 的有功功率。可见本文所提出的下垂控制策略的直流电压控制能力和有功功率分配能力都要优于文献[10]所提出的策略。

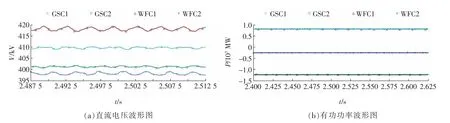
图13 本文所提出的自适应下垂控制稳态仿真图Fig.13 Steady state simulation diagrams of adaptive droop control proposed in this paper

3.2 动态仿真分析

3.2.1 功率阶跃变化

设置送端换流器的有功功率参考值定时阶跃，模拟风电场随机出力的特性，验证本文所提出的自适应下垂控制在功率波动时的稳定性及直流电压控制能力。设置送端换流器的初始状态为WFC1 和WFC2 各向直流网络输入300 MW 的有功功率，当1.5 s 时，两个换流器的输入功率阶跃至500 MW；当2.0 s 时，两个换流器的输入功率又降低至200 MW，直流电压和有功功率随时间变化的仿真结果如图14 所示。

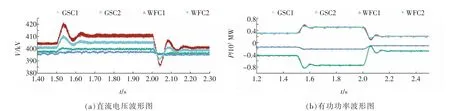
图14 模拟功率波动仿真图Fig.14 Simulation diagrams of simulated power fluctuation

从图14 中可以看出，当1.5 s 时MTDC 送端换流站输入直流网络的有功功率从600 增加到1 000 MW，此时系统输入大功率大于输出的功率，导致系统直流电压升高。随后自适应下垂控制器发生作用，根据式（16）增大GSC1 和GSC2 的功率参考值，受端换流器接收的功率分别从142.5 和432.8 MW 增大到223.2 和745.5 MW。考虑MTDC 系统的损耗后，整个系统的输入输出功率达到新的平衡点，直流电压分别从395.8 和397.7 kV 增加至396.6 和399.4 kV后再度稳定。而当2.0 s 时，送端换流站输入直流网络的功率从1 000 降低到400 MW，此时直流网络输出功率大于输入功率，导致直流电压降低，下垂控制器根据式（16）减小GSC1 和GSC2 的功率参考值，使受端换流站接收的功率分别降至109.3 和280.5 MW，MTDC 系统输入输出功率再度达到平衡，直流电压分别降至395.2 和396.5 kV 后重新稳定。整个过程中GSC1 和GSC2 直流电压直接接受下垂控制器调节，故电压变化较小，WFC1 和WFC2运行于有功功率控制模式，直流电压未受直接控制，故电压波动较大，但基本满足系统安全运行的要求。

当系统输入功率发生变化时，在下垂控制器的作用下，直流电压、有功功率等经过短时间的动态过渡过程，找到新的平衡点，进入稳态阶段。由仿真结果可知，当MTDC 系统的有功功率发生变化时，自适应下垂控制器能够及时响应变化，做出调整，使系统重新回到稳定状态。

3.2.2 换流站退出运行

换流站因为检修等原因中断退出运行是MTDC系统的常见工况，通常被称为N-1 运行。从理论上来说，采用下垂控制的众多换流站中如果有一个站退出运行，那么其他采用下垂控制的换流站可以继续维持系统直流电压稳定并按一定的比例分配不平衡功率。对采用本文所提出的自适应下垂控制策略的MTDC 系统进行N-1 运行测试仿真，以验证所提出策略的可靠性。

如图15 所示，MTDC 系统的初始状态是WFC1和WFC2 各自向直流网络输入500 MW 的有功功率，2.0 s 时交流断路器断开，GSC1 不再向交流系统输送功率，即流经GSC1 的有功功率降至0。此时系统仅余GSC2 向外输出功率969 MW，系统输出功率小于输入功率，导致直流电压从396.7 升高399.7 kV，随后GSC2 的下垂控制器将GSC2 的有功功率参考值增大，使得系统重新回到平衡状态。GSC1 退出运行后，不再有功率流经GSC1，故GSC1 直流电压与GSC2 直流电压基本相同，除了在GSC1 退出时有短暂（0.2 s）较大的电压波动（但仍在电压限制范围内），其他换流站直流侧电压波动范围波动较小，整个系统的运行状态较为平稳。

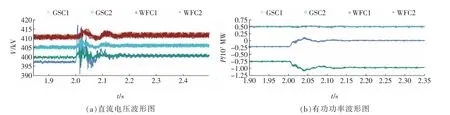
图15 N-1 运行仿真图Fig.15 Simulation diagrams for N-1 operation

由仿真结果可以看出，采用本文所提出的自适应下垂控制策略的MMC-MTDC 系统能够在某一换流站退出运行后保持稳定运行，无需换流站间通讯，剩下的换流站能够自动分配不平衡功率，无需调度系统重新计算电压和功率的参考值，对于换流站数量较多的MTDC 系统具有更加广阔的应用前景。

4 结论

本文介绍了MMC-MTDC 系统的拓扑结构，建立了MMC 的戴维南等效模型。直流电压是MTDC系统中功率平衡和稳定运行的指标，针对采用传统下垂控制器在极端情况下直流电压控制效果较差的问题，根据传统下垂控制的功率-电压特性关系，确定新的功率-电压耦合关系，结合采用下垂控制的换流站实时状态，提出了一种新的直流电压自适应下垂控制策略。在传输功率较低时，MTDC 系统侧重功率分配的精度；在传输功率较高时，系统增强直流电压控制能力。通过控制效果分析和搭建仿真模型，验证了所提出直流电压自适应下垂控制策略的有效性，该策略相比于现有的下垂控制方案，具有更好的直流电压调节效果，同时也兼顾了MTDC系统功率分配能力，可以有效地处理换流站过载问题。控制器设计原理和思路更加清晰，具有十分广阔的研究与应用价值。未来将要结合MTDC 所连接的交流系统的动力学，研究交流电网频率、有功功率和直流电压的耦合关系，研究通过MTDC 系统参与交流电网调频的能力。