基于反馈控制的分数阶复值神经网络的Hopf 分岔

宋倩倩，程尊水

（青岛科技大学 数理学院，山东 青岛 266061）

随着科学与技术的发展，涉及脑科学、数学科学、智能控制等多个领域的神经网络被广泛应用于分类[1]、图像识别[2-3]和优化[4]等多个方面。探索神经网络性质的有效方法是分析网络的动力学性能，因此，神经网络的动力学行为引起越来越多学者的研究兴趣，其中稳定性和分岔（分支）[5-6]是神经网络动力学中的重要特性，例如Wang 等[6]人研究了三对角双向联想记忆（bidirectional associative memory，BAM）神经网络模型的稳定性和Hopf 分岔特性。此外，神经网络的分岔、振荡、混沌和同步[7-9]等动力学性质也是当前的研究热点[8-9]。

分数阶微积分涉及任意阶的积分和导数。不同于整数阶系统，分数阶系统具有无限遗传和记忆能力的优点，这也使得分数阶模型被广泛应用于物理和工程等领域。其中，在信号传输中会不可避免地出现时滞，时滞的存在会对系统的动态性能产生影响，导致系统失去稳定性。因此，对具有时滞的分数阶神经网络模型进行稳定性和分岔分析就显得非常必要，也引起了研究者的广泛兴趣[10-13]，例如Huang 等[12]人研究了高维分数阶神经网络中由自连接时滞引发的分岔问题。

近些年来，具有时滞的分数阶神经网络的动力学分析取得了丰硕的研究成果，推动着人们去扩展现有的分数阶网络模型。其中，具有时滞的分数阶复值神经网络（fractional complex-valued neural networks，FCVNNs）就是在分数阶实值神经网络（fractional real-valued neural networks，FRVNNs）的基础上发展起来的。与一般的分数阶实值神经网络不同，具有时滞的分数阶复值神经网络的状态、连接权重和激活函数都是复数，因此它可以解决更复杂的问题，获得更新的研究成果[14-19]。例如Yuan 等[17]人对具有时滞的二元分数阶复值神经网络进行了研究，这也激励了我们对这类网络进行更深入的探讨。

在分数阶神经网络中，学者们为了得到理想的分岔行为，针对不同的网络提出了多种控制策略，常见的控制方法有PD 控制[20]、混合控制[21]和反馈控制[22]等。这些控制方法不仅为网络控制提供了理论帮助，也在化学工程和电力工程等领域中发挥了实际效益[23]。

本文的主要贡献如下：1）通过设计反馈器对具有延迟的分数阶复值神经网络模型进行控制，并分析了受控系统的稳定性和分岔行为；2）给出了受控系统产生Hopf 分岔的充分条件；3）给出了产生分岔的临界参数值，分析了反馈增益参数与阶数对系统分岔行为的影响。

1 问题描述

在文献[16]中，Huang 等人研究了具有离散时滞的二元延迟分数阶复值神经网络，该网络模型为

Yuan 等[17]人进一步将泄露时滞引入上述模型，得到

在本文中，我们考虑同时具有泄露时滞和离散时滞的三元分数阶复值神经网络，并为该系统设计了时滞反馈控制器，数学模型表示为

其中：q∈（0，1]；zj（t）（j=1，2，3）是复值状态；μj（j=1，2，3）是正实数；aj，bj，cj（j=1，2，3）∈C 表示连接权重，均取为复数值；τ 是时滞；f（·）是激活函数；K是反馈增益参数。

（H1）zj=xj+iyj（j=1，2，3），其中xj，yj分别代表zj的实部和虚部，i 是虚数单位。

（H2）连接权重aj，bj，cj（j=1，2，3）可以表示为

（H3）激活函数f（·）的实、虚部表示为f=fR+ifI。

（H4）f（·）的实、虚部对xj，yj的偏导存在且连续，并有fR（0，0，0）=0，fI（0，0，0）=0。

2 时滞反馈控制器下的Hopf 分岔分析

根据（H1）—（H4），对系统（3）分离实部和虚部，可以得到如下的等价模型：

令x1（t）=U1（t），y1（t）=U2（t），x2（t）=U3（t），y2（t）=U4（t），x3（t）=U5（t），y3（t）=U6（t），则系统（4）变换后的线性模型为

其中aij（i，j=1，2，3，4，5，6）的定义见附录A。线性系统（5）对应的特征方程为

其中m1=μ1-a11+K，m2=μ1-a22+K，m3=μ2-a33+K，m4=μ2-a44+K，m5=μ3-a55+K，m6=μ3-a66+K。

式（6）可以等价写成：

其中，N1，N2，N3，…，N25，N26，N27的定义详见附录B。

2.1 τ≠0 时式（7）特征根的存在性分析

式（7）两边同乘e3sτ，可得

其中，Aj，Bj（j=1，2，3，…，7）的表达式见附录C。下面分两种情况对式（9）进行讨论。

将上式两端平方，得

令cos ωτ=x，并将式（10）两边同时除以d1，式（10）可改写为

如果e1，e2，e3，e4，e5，e6满足（H5），则式（11）可以化成如下形式：

两边开方并移项，得

针对方程（12），有下面两种可能：

（i）取式（12）中的

由式（14）可以求解出

把式（15）代入式（9）的第2 个式子可求得sin ωτ的表达式，并记为

至此，我们就得到了关于ω 的方程。假设方程（17）有一系列的正实根{ω1k}，k=1，2，3，…，则由式（15）可求出

（ii）取式（12）中的

求解上述方程得一系列的正实根{ω2k}，k=1，2，3，…，再从cos ωτ=F3（ω）中推得

经讨论可知，若方程（17）或方程（20）有解，特征方程（7）在下就有相应的纯虚根与之对应。

求解出{ω3k}，{ω4k}，k=1，2，3，…，以及它们分别所对应的参数表达式

2.2 τ=0 时式（7）特征根的存在性分析

当τ=0 时，特征方程（7）可改写为

由Routh-Hurwotz 准则可知，如果（H6）成立，则当τ=0 时方程（7）所有的根都具有负实部。

2.3 Hopf 分岔发生的横截条件分析

令s（τ）=a（τ）+ib（τ）是式（7）满足a（τ0）=0，b（τ0）=ω0的特征根，即±iω0是τ=τ0时式（7）的一对纯虚根。

让式（7）两边同时对τ 求导得

其中，

设W1，W2是W（s）在s=iω0时所对应的实部和虚部，V1，V2是V（s）在s=iω0时所对应的实部和虚部，当s=iω0时有

W1，W2，V1，V2详见附录D。

如果（H7）成立，则系统（3）就满足Hopf 分岔发生的横截条件

综上，当（H1）—（H7）成立时，有下述定理。

定理1当τ=τ0时，系统（3）在平衡点O（0，0，0）处产生Hopf 分岔：

i）当τ∈[0，τ0）时，系统（3）的平衡点O（0，0，0）是渐进稳定的；

ii）当τ ＞τ0时，系统（3）的平衡点O（0，0，0）失去稳定性，并产生Hopf 分岔。

3 数值模拟

本节通过几个实例讨论阶数q 和反馈增益参数K 对系统动力学分岔行为的影响，仿真结果进一步验证了上述理论分析的正确性。

例1选取激活函数f（z）=tanh（x）+tanh（y）+i（tanh（x）+tanh（y）），该激活函数满足（H3），（H4），求得系统（3）的平衡点为O（0，0，0）。令q=0.98，K=-0.2，μ1=μ2=μ3=1，a1=0.3+2i，b1=-0.2-0.4i，c1=-0.2-i，a2=0.2+0.5i，b2=-2-0.1i，c2=1+0.4i，a3=1.2+i，b3=-0.2-0.6i，c3=-0.8-i。借助MATLAB 可计算出临界频率ω0=2.988 1 和分岔临界值τ0=0.334 7。图1 为K=-0.2，τ=0.31 ＜τ0时系统（3）的波形图和相位图，图2为K=-0.2，τ=0.31 ＜τ0时系统（3）的三维轨迹图，图3 为K=-0.2，τ=0.39 ＞τ0时系统（3）的波形图和相位图，图4 为K=-0.2，τ=0.39 ＞τ0时系统（3）的三维轨迹图，图5 为K=-0.2 时系统（3）z1（t）的实部和z2（t）的虚部与τ 的分岔图。图1 和图2 表明当τ=0.31 ＜τ0时平衡点O 是渐进稳定的，但当τ=0.39 ＞τ0时系统（3）失去稳定性并且在平衡点O 处产生周期解（图3 和图4）。图5 验证了上述求得的分岔结果是正确的。

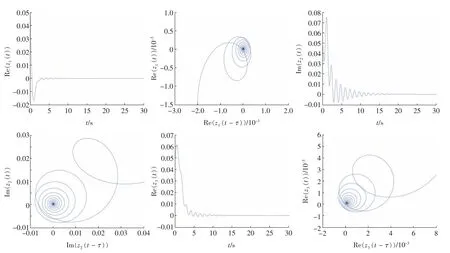
图1 K=-0.2，τ=0.31 ＜τ0 时系统（3）的波形图和相位图Fig.1 Waveform plots and phase portrait of system（3）when K=-0.2，τ=0.31 ＜τ0

图2 K=-0.2，τ=0.31 ＜τ0 时系统（3）的三维轨迹图Fig.2 The 3D trajectory diagram of system（3）when K=-0.2，τ=0.31 ＜τ0

图3 K=-0.2，τ=0.39 ＞τ0 时系统（3）的波形图和相位图Fig.3 Waveform plots and phase portrait of system（3）when K=-0.2，τ=0.39 ＞τ0

图4 K=-0.2，τ=0.39 ＞τ0 时系统（3）的三维轨迹图Fig.4 The 3D trajectory diagram of system（3）when K=-0.2，τ=0.39 ＞τ0

图5 K=-0.2 时系统（3）z1（t）的实部和z2（t）的虚部与τ 的分岔图Fig.5 Bifurcation graph of Re（z1（t））and Im（z2（t））versus τ for system（3）when K=-0.2

接下来我们分析反馈增益参数K 对系统（3）动力学行为的影响，这里保持q 和a1，b1，c1，a2，b2，c2，a3，b3，c3的取值不变。令τ=0.39，K=-0.1，-0.2，-0.3。图6 为τ=0.39，K=-0.1，-0.2，-0.3 时系统（3）的波形图和相位图，图7 为τ=0.27，K=0.3，0.55 时系统（3）的波形图和相位图，图8 为反馈增益参数K 对临界值τ0的影响。图6 表明K 的增加使得极限环振幅变大。此外，当取K=0.3 时，求得临界值τ0=0.288 1。若固定τ=0.27 而改变K 的值，则当K 从0.3 增加到0.55 时，系统（3）丢失稳定性，即Hopf 分岔会提前发生（图7）。图8 表明τ0将随着K 的增加而减小，黄色区域D 是系统（3）的稳定区域，系统（3）将在边界曲线L 上经历Hopf 分岔，当K和τ 的取值超出区域D 时，系统（3）将从平衡点O处分支出周期解。

图6 τ=0.39，K=-0.1，-0.2，-0.3 时系统（3）的波形图和相位图Fig.6 Waveform plots and phase portrait of system（3）with K=-0.1，-0.2，-0.3 when τ=0.39

图7 τ=0.27，K=0.3，0.55 时系统（3）的波形图和相位图Fig.7 Waveform plots and phase portrait of system（3）with K=0.3，0.55 when τ=0.27

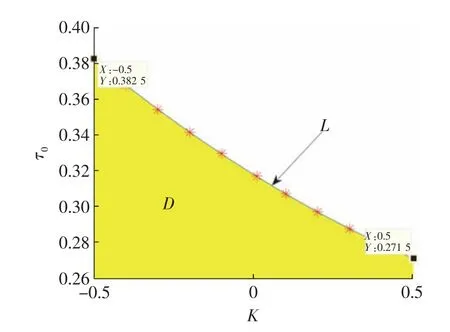
图8 反馈增益参数K 对临界值τ0 的影响Fig.8 Influence of the feedback gain parameters K on critical value τ0

例2仍取激活函数f（z）=tanh（x）+tanh（y）+i（tanh（x）+tanh（y）），令K=0.1，μ1=0.5，μ2=0.7，μ3=1，a1=-0.7-1.6i，b1=-0.3-0.4i，c1=-0.3-1.2i，a2=0.1+0.6i，b2=-1.9-0.3i，c2=1+0.4i，a3=1.1+0.7i，b3=0.2+0.4i，c3=-0.8-i，改变阶数q 的值。当阶数q 增大时，τ0也随之增大，这意味着Hopf 分岔的发生将被推迟（图9）。

图9 阶数q 对临界值τ0 的影响Fig.9 Effect of the order q on critical value τ0

4 总结

本文研究了反馈控制下时滞的分数阶复值神经网络的分岔与控制问题。以时滞作为分岔参数，根据Routh-Hurwotz 准则求得平衡点的稳定区间，得到了系统产生Hopf 分岔的充分条件；通过复杂的计算，得到发生Hopf 分岔的参数临界值；最后，借助数值仿真对理论结果进行了验证，并进一步讨论了如何提前或延迟Hopf 分岔。

附录Aaij（i，j=1，2，3，4，5，6）的定义

附录BN1，N2，…，N26，N27的定义

附录CAj，Bj（j=1，2，3，…，7）的表达式

附录DW1，W2，V1，V2的表达式