基于随机k-近邻集成算法的网络流量入侵检测

张承烨，李卓轩，曹进德*

（1.东南大学 人工智能学院，江苏 南京 211189；2.东南大学 数学学院，江苏 南京 211189；3.江苏省网络群体智能重点实验室，江苏 南京 211189）

随着互联网技术的快速发展与普及，网络安全问题变得日益突出，木马程序、蠕虫病毒、DDOS（distributed denial of service）攻击等大量的威胁与安全隐患扰乱了社会正常情况的运作与经济的可持续发展。随着人工智能技术应用的发展[1-2]，网络流量异常检测方法作为网络安全系统中入侵检测技术实现的核心，受到国内外学者的广泛关注。

熊钢等[3]针对网络空间安全中面临的威胁进行了综述，将入侵检测系统功能分为两大类：异常检测软件系统和签名检测系统。异常检测软件系统在检测未知攻击方面表现更理想，然而会产生很高的误报率。因此，提高入侵检测系统的检测精度和学习速度仍然是一项艰巨的任务。Papamartzivanos 等[4]提出了名为Dendron 的入侵检测系统，通过遗传算法对决策算法进行优化，旨在生成准确且无偏的决策树，能够检测常见和罕见的侵入性攻击。生龙等[5]为了提高网络入侵检测模型的准确率与泛化性，采用核主成分分析提取入侵性攻击的特征，通过改进的引力搜索算法对混合核极限学习机进行优化。徐国天[6]提出一种基于裁剪树方法优化的k-近邻（knearest neighbor，k-NN）的入侵检测模型，维持较高查询效率。王月等[7]提出名为imTk-NN 的网络入侵检测模型，采用改进的三元组网络和k-近邻算法进行组合预测，精度和效率都有大幅提升。

综上，本文提出一种新的k-NN 集成算法——随机k-NN（random k-nearest neighbor，Rk-NN）算法，应用于网络异常流量检测。主要包含以下部分：1）提出一种基于熵权法与变异系数法的集成赋权欧氏距离；2）采用一种随机策略的集成方法，首先采用bootstrap 再抽样技术，对抽样后的数据集随机选取特征构成随机子空间，然后生成多个组件k-NN 分类器，最后对整个集成方法进行并行优化；3）对每一个子k-NN 分类器按照均匀分布随机生成k 值。

1 相关理论基础

1.1 k-NN 算法

k-NN 分类算法[8]简单、易于实现，是机器学习领域的一个经典机器学习算法，引起了人们的广泛关注[9]。k-NN 算法模型已广泛应用于文本挖掘、模式识别等领域，它是一种基于实例的学习法，可以根据被预测对象与已知对象之间的相似度进行归类，并不能显式地构建模型，k-NN 算法模型过于依赖待分类具体实例与训练集中最近的k 个邻居。

表1 k-NN 算法Tab.1 k-NN algorithm

算法1 中：l 为类标签；yi是第i 个近邻的类标签；V（·）为一个指示函数，当条件为真时返回1，当条件为假时返回0。

与神经网络和决策树分类器有许多参数不同，k-NN 分类器只有两个参数，即用于计算给定测试样本与训练样本的距离度量和邻居k 的数量，这使得k-NN 的优化研究具有挑战性。k-NN 可以根据与该实例最近的k 个实例进行归类，然而k 的优与劣将完全决定着k-NN 分类的使用效果。诚然，k-NN 算法的关键之一在于如何采纳一个合理的k 值[10]。如果k 值取得过小，则算法易受噪声的影响，使分类结果不稳定；k 值取得过大，则近邻集中含有太多其他类别的实例，导致分类错误，同时，过大的k 值也会增加算法的时间总开销。理论上可以通过采用枚举法，循环遍历所有可能的k 值，最后从中选出最好的k 值作为近邻数。但在实际应用中，枚举法带来的时间总开销一般说来是根本无法接受的。

1.2 bagging 集成方法

1996 年，Breiman[11]提出bagging 集成方法，它是最早也最简单的集成算法之一。借助bootstrap 抽样从原始训练集得到多个同等规模的训练集合的子集，接着使用相同学习算法模型在这些训练集上训练出多个基分类算法，最终以多数投票方式组合所有分类结果。

相对于新的未见实例，由训练阶段得到的个体分类算法分别对其所属类别投票，总票数最大的类别即是最终的决策结果。所提出的bagging 集成算法具体直观有效，尤其适用于数据集很小的情景。表2 给出了提出bagging 算法描述[2]。

表2 bagging 算法Tab.2 bagging algorithm

虽然bagging 集成方法在决策树（decision tree，DT）[12]和神经网络（neural network，NN）[13]上取得了巨大的成功，但它很难在k-NN 分类器上很好地工作[11]。因为k-NN 是一个稳定的分类器，而bagging 使用bootstrap 再抽样技术来生成准确但多样的组件分类器，这对不稳定的机器学习方法如决策树和类感知机算法的工作是更有效的。

2 Rk-NN 算法

2.1 集成赋权距离

为了更合理地分析各个数据对象之间的差异程度，本文利用一种信息熵与变异系数结合的集成赋权法来计算各数据对象的赋权欧式距离。变异系数法通过利用各项特征反映的信息计算得到特征的权重，它反映的是特征值的差异程度及数据的分布情况，假设数据集X 有m 个对象和n 个特征，变异系数权重计算方法为

其中：δi为第i 项指标的标准差；为第i 项指标的平均数；为变异系数法确定的第i 个特征权重。

在信息论中，熵是对数据不确定性的一种度量和描述，熵值越大，数据不确定性越小；反之亦然，熵值越小，不确定性则越大。一个方案的无序性和随机性的程度可以由熵特性来确定。此方法可以消除单位或平均值不同对多种数据变异程度的影响。假设数据集X 有m 个对象和n 维属性，设标准化后的数据为xij，熵权计算方法为

其中：ej为第j 个特征的熵值，k ＞0，ej＞0，k 与样本量m 有关，一般令k=1/ln（m），则0≤ej≤1；对于第j 项指标，指标值xij差异越大，熵值越小，gi越大，在计算距离时占比越大；权重为熵权法确定第j 个特征的权重。

本文通过线性加权组合的方法，综合熵值法与变异系数法的权重确定结果，增加权重确定的科学性。其计算公式为

最终通过集成赋权法，确定赋权欧氏距离为

加权欧氏距离可以用来判断不同数据对象之间的相似程度，可以提高分类精度。

2.2 随机策略优化

为了提高k-NN 的预测精度，首先进行随机特征（输入变量）选取，在引入特征随机性的同时，减小相关系数而保持强度不变。本文对训练集的输入属性进行随机扰动，从最初训练集的属性集中抽取出若干个属性子集，基于每个子集训练一个k-NN组件分类器，不同的“子空间”提供了观察数据的不同视角。本文通过设定特征抽取比例α，对训练集的原始输入特征进行按比例随机选取，再进行bootstrap 抽样，最终生成随机特征空间，过程如表3 所示。显然，上述方案能解决bagging 算法对于k-NN这种稳定分类器优化效果差的问题。

表3 RS 算法Tab.3 RS algorithm

通常选取超参k 值进行k-NN 算法的优化[14]，为数据集找到最优k，并依此进行分类。因为没有先验知识，直接指定k 值具有很大的盲目性，同时，穷举法又由于时间开销过大而不可取。本文提出一种对多个k-NN 组件分类器k 值的选取方法，按照区间Ω=[N，2N+1]均匀分布生成单一k-NN 组件分类器的k 值，为

其中：i 为k-NN 组件分类器编号；M 为k-NN 组件分类器总个数。算法过程如表4 所示。

表4 Rk-NN 算法Tab.4 Rk-NN algorithm

由于算法有良好的并行性，本文对Rk-NN 算法分别实现数据处理的并行化，实现模型训练的并行化。

2.3 基于Rk-NN 算法的网络入侵检测模型

基于以上内容，本文提出了一种新型的网络入侵检测模型——Rk-NN 算法的网络入侵检测模型，结构如图1 所示[5]。

图1 基于Rk-NN 算法的网络入侵检测模型[5]Fig.1 Network intrusion detection model based on Rk-NN algorithm[5]

该模型的具体步骤如下：

Step1 输入数据集，初始化Rk-NN 算法；

Step2 对数据集进行划分，拆分成训练集和测试集；

Step3 使用预处理的训练数据集生成历史数据搜索空间；

Step4 使用测试数据集评估获得的最佳Rk-NN 模型的性能；

Step5 输出模型检测结果的评估指标。

3 实验与分析

3.1 实验数据

为了验证Rk-NN 算法的有效性，选取6 组UCI数据集中的公开测试数据（见表5）和KDD99 数据集进行实验。

表5 UCI 数据集[6]Tab.5 UCI dataset[6]

KDD99 数据集中共包含23 种攻击类型，可以分为四大攻击类别：DoS、PRB、U2R 和R2L[15]。由于利用KDD99 完整的数据集在进行机器学习算法训练时很复杂，因此大多数研究人员都使用了KDD99数据集中10%子集作为实验数据。表6 给出了KDD99数据集的详细信息，其中训练数据集和两个测试数据集分别表示为T0、T1和T2。训练数据集T0与测试数据集T1一起用来验证Rk-NN 算法的有效性。此外，本文还利用测试数据集T2进行Rk-NN 算法与其他研究模型的性能比较。

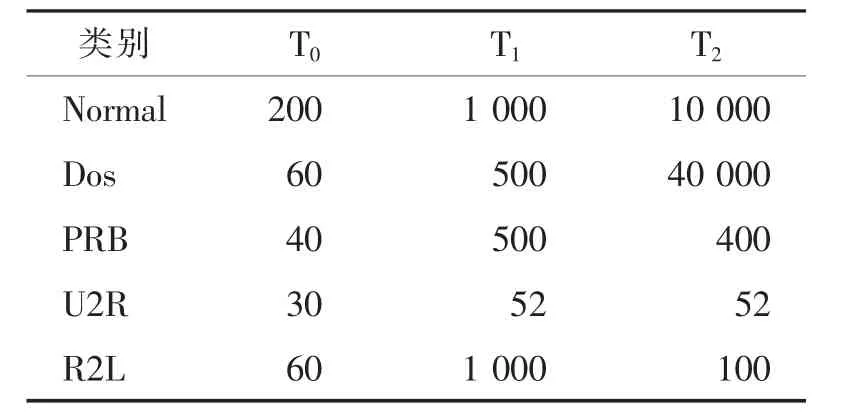
表6 KDD 数据集划分[7]Tab.6 KDD dataset division[7]

3.2 实验结果评价指标

为了评估Rk-NN 算法的性能，采用准确率（accuracy，Acc）和F-score 值，对算法在UCI 数据集上的表现进行评价。为了评估Rk-NN 算法在网络入侵检测中的效果，采用精准率（precision）和Fscore 值作为每类攻击的评估指标；准确率（accuracy，Acc）、召回率（recall）、平均F-score（mean F-score，MF）作为数据集整体的评估指标。在数据集中的网络连接可以分为正常（标记为0）、攻击（标记为1，2，3，4）两大类。计算方式如表7 所示。

表7 评价指标Tab.7 Evaluation index

其中：TP（真阳性）为正样本被正确预测为正样本；TP（假阳性）为负样本被错误预测为正样本；TN（真阴性）为负样本被正确预测为负样本；FN（假阴性）为正样本被错误预测为负样本，在F-score 中令β=1。

3.3 实验结果分析对比

3.3.1 Rk-NN 算法在UCI 数据集上的表现

在UCI 数据集上将Rk-NN 算法与同类变种算法进行对比（见表8），对比算法分别为：k-NN 算法、bagging 集成的k-NN 算法和改进距离的k-NN 算法，其中k-NN 算法，bagging 集成的k-NN 算法采用欧氏距离，Rk-NN 算法采用集成赋权距离。

表8 在UCI 数据集上的不同算法比较Tab.8 Comparison of different algorithms on UCI dataset %

由表8 可看出，Rk-NN 算法具有更好的分类精度。相比欧式距离，Rk-NN 算法采用集成赋权距离能有效挖掘数据之间的联系，即Rk-NN 通过权重计算能更有效描述不同样本之间的联系，具有更好的分类性能；不仅保持bg k-NN 集成算法的优点，能有效描述样本之间的联系，而且通过随机集成策略构建随机子空间，Rk-NN 算法能有效利用数据集上的信息形成分类器间的差异，强化不同分类器中信息的重要性，提高集成的效果，具有更高的分类性能。Rk-NN 算法相较k-NN 算法在准确率上平均提升了13.00%，在平均F-score 指标上平均提升了15.20%。

3.3.2 Rk-NN 算法在KDD99 数据集上的表现

本文利用训练数据集T0和测试数据集T1对Rk-NN 算法性能进行分析，对于不同攻击类别进行比较，如图2 所示，性能如表9 所示。

图2 Rk-NN 算法检测结果Fig.2 Rk-NN algorithm detection results

表9 不同攻击的检测性能比较Tab.9 Comparison of detection performance of different attacks %

如表9 所示，Rk-NN 算法整体达到了一个较高水平，针对Normal 类别，召回率达到99.40%，但精准率只有90.86%，存在误报的情况；对于Dos 攻击能够精准识别，精准率达到99.60%，同时Fscore和召回率也分别达到了99.70%和99.80%；对R2L，U2R 和PRB 的识别，本文算法也达到了一个较高的水平。

3.3.3 Rk-NN 算法与其他算法的对比

对于在测试数据集T2上，将本文提出的基于Rk-NN 算法的网络入侵检测模型与其他常用的机器学习算法如：支持向量机（support vector machine，SVM）算法、k-近邻（k-nearest neighbor，k-NN）随机森林（random forests，RF）模型、决策树（decision tree，DT）算法、极限梯度树（extrme gradient boosting，XGBoost）模型算法分别进行测试，结果如表10所示。

表10 本文算法与其他算法比较结果Tab.10 Compare with other algorithms %

Rk-NN 模型检测结果的评估指标准确率、平均F-score 和召回率的值分别为99.05%、97.44%和91.96%。本文算法相较SVM 算法在准确率、平均F-score、召回率分别提升了1.41%、2.04%和42.95%；相较DT 算法在准确率、平均F-score、召回率分别提升了2.55%、1.29%和51.25%；相较XGBoost 算法在准确率、平均F-score、召回率分别提升了1.21%、0.15%和27.65%；相较RF 算法在平均F-score 没有提升，在准确率、召回率分别提升了0.37%、12.16%。可以看出，与其他方法相比，本文算法在流量入侵检测上具有更高的分类精度并且有更高的召回率。这充分说明Rk-NN 模型在KDD99 数据集上具有更好的性能。

4 结论

本文所提的Rk-NN 模型在计算距离时引入一种集成赋权的欧式距离，采用熵权法和变异系数法计算不同特征之间的权值差异性，使得能够有效识别出关键特征。加入集成赋权欧式和随机策略优化方法，提升各个子分类器差异程度，提高了在网络入侵检测中的识别精度。Rk-NN 模型有良好的并行性，本文通过并行优化，提升算法运行效率。下一步将通过对Rk-NN 模型进行模型剪枝，提升模型精度和算法效率，建立更加实时高效的检测模型，完善网络流量入侵的检测体系。