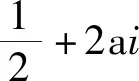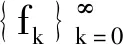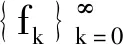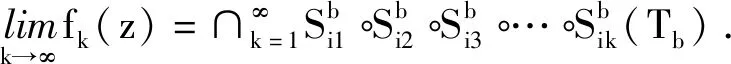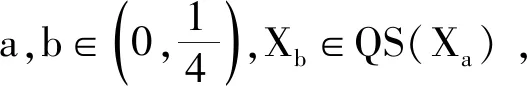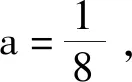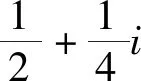一类平面自相似集的共形维数

张田莉,杨红霞

(湖北大学数学与统计学学院,应用数学湖北省重点实验室,湖北 武汉 430062)

0 引言及主要结论

从初始集Ta出发,我们在平面上定义一类自相似集的迭代函数系(IFS)为

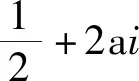
满足开集条件.

图1 自相似集Xa的一级生成方式和二级生成方式

从而由文献[3,定理9.3]可知：方程

的唯一正数解即为Xa的Hausdorff维数,因此有

2001年,Bishop和Tyson在文献[1]中给出了平面上一类“天线”集的共形维数.2020年,党云贵和文胜友在文献[13]中证明了平面上一类自相似集的共形维数为1 且该类自相似集不是拟对称极小集.2021年,党云贵在文献[14]中证明了Tyson型集和地毯Sp的拟对称极小性,其他相关结论可参见文献[2-6].本文在文献[1,13,14]的基础上研究讨论了由上述IFS所生成的一类平面自相似集的共形维数及拟对称极小性.下面给出本文中的主要结论.

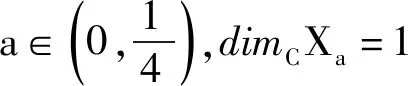
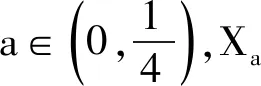
1 预备知识

本节先回顾定理证明中所需用到的相关定义及结论,同时给出定理证明中用到的命题.具体可参见文献[7-12].

定义1[7-8]设X,Y为度量空间,如果存在一个同胚映射f：X→Y以及一个同胚映射η：[0,+∞)→[0,+∞),使得对X中的任意不同的3点x,y,z,都有

则称映射f为拟对称映射,此时称度量空间X与Y是拟对称等价的.

定义2[9]设X为度量空间,定义X的共形维数

dimCX=inf{dimHY：Y是与X拟对称等价的度量空间}.

并称X是拟对称极小的,如果dimCX=dimHY.

定义3[10]设f是n上的自同胚映射,称f是H-拟共形映射,如果存在常数H>0,对任意x∈n,r>0有

dimCX≤inf{dimHf(X)：f：n→n是拟共形映射}

(2)

命题1[10]设{fj}j≥1是区域Ω⊂n上的H-拟共形映射序列,若对任意的j,{fj}都逐点收敛于Ω上的同胚映射f,则f也是H-拟共形映射.

我们在计算一个集合的Hausdorff维数时,往往比较容易得到其维数的上界,而对于其下界的估计常用到质量分布原理.

命题2[11]设X是一个度量空间,μ是一个支撑在X上的正有限的Borel测度,如果存在常数c>0及s>0,对任意的x∈X,0

μ(B(x,r))≤crs,

则dimHX≥s.

2 定理1的证明

对每个正整数k,Ak={i1i2…ik：ij∈A,1≤j≤k}表示所有长为k的词的集合;A*=∪k≥0Ak表示所有长为有限的词的集合.如果ω∈A*,我们用|ω|表示词ω的长度;A∞={i1i2…in…：ij∈A,j≥1}为由A生成的符号空间,它表示所有长为无穷的词的集合.当σ∈Ak时,记Sσ=Si1∘Si2∘…∘Sik,Xσ=Sσ(X),称Xσ为X的一个k级复制.

定理1的证明我们分为两部分：

第二部分：上述定义中的共形维数的下确界不能达到,即对任意与Xa拟对称等价的度量空间Y∈QS(Xa),有dimHY>1.

第一部分的证明：第一步,证明dimCXa≥1.

由Xa的构造可知,Xa是一连通集,所以dimHXa≥1.又连通集的拟对称像是连通的,则dimCXa≥1.

第二步：证明dimCXa≤1.

为此,由命题1即证下面一个引理.

引理1存在2到2的分片仿射映射序列且逐点收敛于f,使得任给有f(Xa)=Xb.

引理1的证明(存在性)设a>b.由图2可知,存在唯一可逆的线性变换f0：2→2,使得f0(Ta)=Tb,且对Ta的每个一级小拷贝都是线性和拟共形的,并且从Pa到Pb是分片仿射映射.此时f1显然是H-拟共形映射.

图2 构造从Xa到Xb的映射

当k≥2时,定义fk：2→2如下：

又由于任给k及σ∈Ak,依次作用fk,fk-1,…,f1,f0的定义有

=…

因此,由(1)(2)式有dimCXa≤1.

综上所述dimCXa=1.

由命题2可知,要证dimHY>1,我们需要在Y上构造一个测度ν满足：对任意的y∈Y,r>0,当B(y,r)⊂Y时,存在仅与η有关的常数C及s>1,使得

ν(B(y,r))≤Crs

(3)

从而由质量分布原理,对Y的任意一族覆盖B(yi,ri)有

故dimHY≥s>1.

事实上,s>1的存在性是显然的.给定k及σ∈Ak,定义dσ=|f(Sσ(0)-f(Sσ(1))|.因为Sσ(0)=Sσ1(0),Sσ(1)=Sσ2(1).所以,由三角不等式有

dσ1+dσ2≥dσ

(4)

又由f的拟对称性,有

因此,结合(4)式可知,存在仅与η的常数N>0,使得

基于上述s>1,定义X上的概率测度μ满足

且具有如下性质.

由于X与是Y拟对称等价的,所以X上的测度μ在映射f的作用下,在Y上自然存在一个拉回测度ν=μ∘f-1.

B(x,r1)⊆f-1(B(y,r))⊆B(x,C2r)

(6)

其中x=f-1y,r1=η-1(1)|f-1y-f-1b|,C2=(η-1(1))-2.

定义

C：={σ：|Tσ|≤r1<|Tσ*|,Tσ∩f-1(B(y,r))≠Ø,σ∈A*}.

使得{Tσ}σ∈C为有限个直径不超过r1的集构成的覆盖f-1(B(y,r))的集类.结合(5)式有

B(x,r1)⊆f-1(B(y,r))⊆∪σ∈C(Tσ∩X)=∪σ∈CXσ

(7)

引理3存在仅与η有关的常数C3,C4>0,使得#C≤C3且对任意的σ,ω∈C有dσ≤C4dω.其中#C表示C中元素的个数.

如果上述结论成立,则定理1得证.因为

如果选取w∈C,使得x∈Xw.由于|Xw|≤r1,因此Xw⊆B(x,r1),由(6)式的包含关系有f(Xw)⊆B(y,r1).于是|f(Xw)|≤2r.另一方面,由拟对称映射的性质有

≤η(2).

取C=(2η(2))sC3C1C4即证.

下面证明引理3成立.

所以计算面积可得,

因此,

#C≤512π(1+C2)2,

又C2仅与η有关,这里令C3=512π(1+C2)2即可.

第二步：σ,ω∈C,由C的定义及式(5)可知,

d(Tσ,Tω)≤2C2r1.

由IFS的选取以及C的定义可得

|Tσ|≤r1<|Tω*|≤8|Tω|,|Tω|≤r1<|Tσ*|≤8|Tσ|.

因此,

不妨设|Tw|≤|Tσ|,由上式及X的构造中基本三角形的大小关系,有

|Tσ|=|Tω|或|Tσ|=2|Tω|或|Tσ|=4|Tω|

(8)

下面考虑Tσ与Tω的位置关系.

(1)Tσ∩Tω={z}.

由dσ=|f(Sσ(0)-f(Sσ(1))|及f的拟对称性,有

(2)Tσ∩Tω=Ø.

由X的构造,X中存在连接Tσ与Tω的简单折线γ,并且折线γ中的线段要么是水平的要么是竖直的,使得折线γ的长度满足

因此,可存在σ1,…,σn-1∈A*,使得三角形列Tσ,Tσ1,…,Tσn-1,Tω两两相邻,且折线γ由这些三角形的直径连接而成.由(8)式及X的构造,不妨设这些三角形满足条件：对任意的1≤j≤n-1有

|Tσ|=|Tσj|,

即|Sσ(0)-Sσ(1)|=|Sσj(0)-Sσj(1)|.这里σj不一定属于C.从而有

≤2C2C4r1.

故n≤16C2C4r1+1,并且n仅依赖于η.

进而,由f的拟对称性和dσ的定义有

dσ≤η(1)dσ1,dσ1≤η(1)dσ2,…,dσn-2≤η(1)dσn-1,dσn-1≤η(1)dω.

即dσ≤(η(1))ndω.取C3=(η(1))n即可.

综上所述,存在仅与η有关的常数C4使得dσ≤C4dω.

至此定理1得证.