关于“三次对称多项式x3+y3+z3-3xyz的因式分解及其应用”的注记

高睿,徐行忠,廖军,刘合国

(1.湖北大学数学与统计学学院,湖北 武汉 430062;2.海南大学理学院,海南 海口 570228)

0 引言

对称多项式和对称函数是代数学、组合学中的重要研究对象,例如MacDonald[4]在其经典著作里深入地阐述了对称函数和Hall多项式在代数学等方面的作用,Stanley[5]在组合学专著中详细介绍了对称函数的基本组合学性质,并给出了其与群表示论、Plya理论的联系．此外,它们在多项式方程理论、代数几何、李代数、特殊函数和理论物理等许多领域也都具有重要而深刻的应用,可见文献[6-9]．

在文献[1-3]里,我们给出了下面的多项式

x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)

=(x+y+z)(x+ωy+ω2z)(x+ω2y+ωz)

(1)

在高等代数、高等数论里的应用,这里ω是1的3次本原单位根．现在,我们要把文献[1-3]的思想继承下来,突破其局限,用不同的证明方法,从不同的角度尽可能地得到一般性结果．

1 不等式证明中的进一步应用

根据(1)式,文献[1]中推论3给出了如下结论．

引理1.1当x,y,z是非负实数,则

等号成立当且仅当x=y=z．

将该结果推广,就得到了著名的AM-GM不等式,即

引理1.2(AM-GM不等式) 若a1,a2,…,an是正实数,则

等号成立当且仅当a1=a2=…=an．

AM-GM不等式有多种证明方法,本研究利用如下Schur不等式给出一种新的证明．

引理1.3(Schur不等式) 设A=(aij)n×n∈n×n的特征值为λ1,λ2,…,λn,则有

等号成立当且仅当A是正规矩阵．

引理1.3的证明由文献[10]中的定理2.3.1和定理2.5.4可得．

下面我们用Schur不等式证明AM-GM不等式．

记

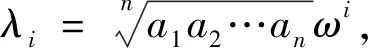
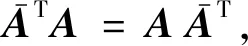
回到(1)式,我们还容易得到,当x,y,z∈+时,x3+y3+z3-3xyz≥0,等号成立当且仅当x=y=z．将该结论推广到更一般的情形,可得如下结果．

定理1.1若x1,x2,…,xn是正实数,则

等号成立当且仅当x1=x2=…=xn．

定理1.1的证明对上的任意多项式t(x1,x2,…,xn),记

则St为对称多项式．设xi∈+,令

显然fi(x1,x2,…,xn)≥0,从而Sfi≥0,且有

左右两边分别相加得

等号成立当且仅当Sfi=0对任意i=1,2,…,n,故x1=x2=…=xn．

2 多项式证明中的进一步应用

在文献[1]中,例10如下所示．

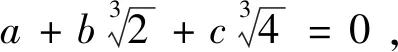
文献[1]中利用整除的相关理论证明了这一结论．本文中我们对这一结果进行推广,用不同的证明方法得到更一般的结果．

定理2.1设a0,a1,…,an-1是有理数,p是素数,且

则a0=a1=…=an-1=0．

定理2.1的证明我们用两种方法给出证明．

证法1不失一般性,可设a0,a1,…,an-1都是整数．设p(x)=xn-p,由艾森斯坦判别法知p(x)在上不可约,另设f(x)=a0+a1x+…+an-1xn-1∈[x],则p(x)和f(x)在上有公共根我们断言在上p(x)|f(x),若不然,由于p(x)是不可约多项式,有gcd(p(x),f(x))=1,从而存在u(x),v(x)∈[x]使得u(x)p(x)+v(x)f(x)=1,将代入有0=1,矛盾!而由于f(x)的次数最多为n-1,p(x)的次数为n,因此f(x)≡0,故a0=a1=…=an-1=0．

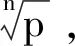
考虑方程组

显然线性方程组有解,从而

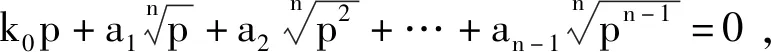
从而

同理可得p|a2,p|a3,…,p|an-1,与假设a0,a1,…,an-1中非零元互素矛盾!从而a0=a1=…=an-1=0．

在文献[2]中,例47如下所示．

例2.2证明：对任意p(x)∈[x],均存在非零整系数多项式q(x),使得p(x)q(x)=f(x3)对某f(x)∈[x]．

该结论可以推广得到下面的结果．

定理2.2对任意f(x)∈[x],均存在非零整系数多项式g(x),使得对任意r∈+,都有f(x)g(x)=h(xr)对某h(x)∈[x]．

定理2.2的证明若f(x)≡0,则对任意0≠g(x)∈[x],都有f(x)g(x)=h(xr)当h(x)≡0．

若f(x)是非零多项式,当r=1时,取g(x)=1,结论显然成立．

当r≥2时,设f(x)=amxm+am+1xm+1+…+anxn,其中am,an≠0．设

h0(xr)=bmrxmr+b(m+1)rx(m+1)r+…+bnrxnr∈[x],

g0(x)=y0+y1x+y2x2+…+ynr-nxnr-n∈[x],

其中bmr≠0．若f(x)g0(x)=h0(xr),即

(amxm+am+1xm+1+…+anxn)(y0+y1x+y2x2+…+ynr-nxnr-n)=bmrxmr+b(m+1)rx(m+1)r+…+bnrxnr．

对比等式左右两边系数,得到关于y0,y1,…,ynr-n,bmr,b(m+1)r,…,bnr的齐次线性方程组

其中ai=0,i>n;yj=0,j>nr-n．

由于未知量个数大于方程个数,从而方程组有非零解,易得bmr可作为自由未知量,不妨取bmr=1,则在上可以解得y0,y1,…,ynr-n,b(m+1)r,…,bnr,那么h0(x),g0(x)∈[x]使得f(x)g0(x)=h0(xr)．此外,显然存在k∈使得kf(x)g0(x),kh0(xr)∈[x],令g(x)=kg0(x),h(x)=kh0(x),得证．

对于更一般的情形,我们有下面结论．

定理2.3对任意f(x)∈[x],均存在0≠g(x)∈[x],使得对任意φ(x)∈[x],都有f(x)g(x)=h(φ(x))对某h(x)∈[x]．

定理2.3的证明设f(x)是n次整系数多项式,在上f(x)=k(x-x1)(x-x2)…(x-xn),则

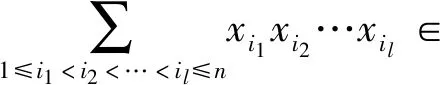
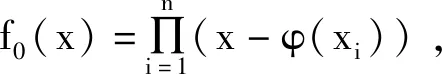
可表示成关于x1,x2,…,xn的初等对称多项式的多项式,从而f0(x)∈[x]．因此F(x)=h0(φ(x))∈[x],故在上f(x)整除F(x),即存在g0(x)∈[x]使得f(x)g0(x)=F(x)=h0(φ(x))．显然存在k∈使得kf(x)g0(x),kh0(φ(x))∈[x],令g(x)=kg0(x),h(x)=kh0(x),得证．

3 一元多项式方程的解法和根式化简

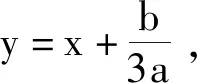
但是对于复数域的子域上的一元三次方程,直观上我们并不能判断有几个根以及根的分布．下面我们从更一般的情况出发讨论一元三次方程根的情况,首先需要一个引理．

引理3.1设是特征0的域,≤,x3+px+q=0是上的一元三次方程,且x2=a,x3=a对任意a∈都有解．若y0,z0∈,且是方程的根,则存在z1∈,使得且y0+z1是原三次方程在上的根．

引理3.1的证明显然在中,或或且y0z0∈,其中ω为1的本原三次单位根(由于特征0,所以ω可以用根式表出

=-q-p(y0+z0)+p(y0+z0)+q

=0.

故x1=y0+z1是方程在上的一个根．

结合(3)式和引理3.1,我们有y0+z1,ωy0+ω2z1,ω2y0+ωz1是原三次方程在上的三个根．下面具体给出根的分布．

定理3.1设是特征0的域,且x2=a,x3=a对任意a∈都有解,若≤,x3+px+q=0是上的一元三次方程,记则有

2) 当Δ≠0时,有

(i) 若x2=Δ在上有解x0,且在上有解．则当ω∉,方程在上有一个根;当ω∈,方程在上有三个根．

(ii) 若x2=Δ在上无解,在上有解x0,且在(x0)上有解．则当ω∈,方程在上有一个根;当ω∉,ω∈(x0),方程在上有三个根;当ω∉(x0),方程在上有一个根．

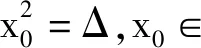
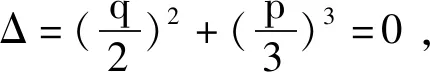
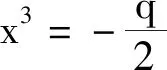
2) 当Δ≠0时,分情况讨论．

(i) 若x2=Δ在上有解x0,且在上都有解,设其中y0,z0∈,则在中,或或且y0z0∈．

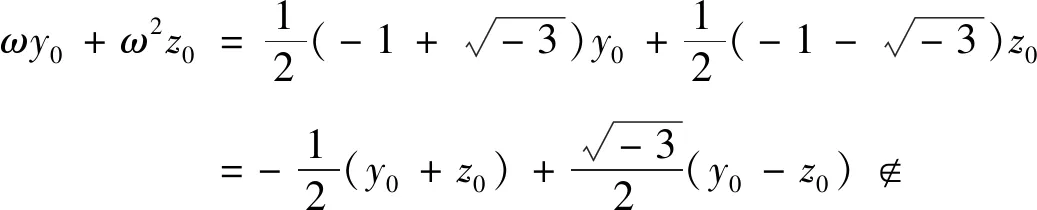
(ii) 若x2=Δ在上无解,作关于的分裂域(x0),其中则在(x0)上两个不同的根为

ωix1+ω3-ix′2=ωix1+ω3-ix2ω3-i=ωi(a+bx0)+ωi(a-bx0)=2ωia∈,

且ωi+1x1+ω2-ix′2=ωi+1(a+bx0)+ωi-1(a-bx0)=(ωi+1+ωi-1)a+(ωi+1-ωi-1)bx0∉,否则x0∈,矛盾!同理有ωi+2x1+ω1-ix′2∉,从而方程在上有一个根．

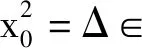
下面证明y0,y1,y2∉．由于则故若y0∈,由于则α是(x0)上的二次多项式的一个根,而[(x0,α)：(x0)]=3,矛盾!所以y0∉．同理有y1,y2∉,因此方程在上无根．

下面证明z0,z1,z2∉,由于则故若z0∈,由于则μ是(x0)上的二次多项式的一个根,而[(x0,μ,ω)：(x0)]=6,矛盾!所以z0∉．同理有z1,z2∉．因此方程在上无根．

推论3.1设≤,x3+px+q=0是上的一元三次方程,记则有

2) 当Δ≠0时,有

(i) 若x2=Δ在上有解x0,且在上有解．则当∩,方程在上有一个根;当∩方程在上有三个根．

(ii) 若x2=Δ在上无解,但在扩域(x0)上有解x0,同时在(x0)上有解．则当∩方程在上有一个根;当∩,(x0)∩方程在上有三个根;当(x0)∩,方程在上有一个根．

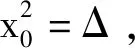
推论3.2设x3+px+q=0是上的一元三次方程,记则有

1) 当Δ=0时,方程在上有三个根,且至少其中两根相等．

2) 当Δ>0时,方程在上有一个根．

3) 当Δ<0时,方程在上有三个根．

推论3.2的证明1) 当Δ=0时,由定理3.1易得．

2) 当Δ>0时,有x2=Δ在上有解,设为在上有解,且∩,方程在上有一个根．

3) 当Δ<0时,有x2=Δ在上无解,域上添加后形成的扩域必为复数域,而在上一定有解,同时∩,(x0)∩故方程在上有三个根．

4 等幂和方程组的求解

在文献[3]中,例40讨论了方程组

自然地,可以考虑将其推广到更一般的情况,即

针对sk=0,1,n(k=1,2,…,n-1,m)的情形,[11]分别给出了关于方程组(4)的解的一般性结果．本节讨论更一般的情形,给出求解(4)的方法．

对于首一多项式f(x)=(x-x1)(x-x2)…(x-xn)=xn-σ1xn-1+…+(-1)nσn,有

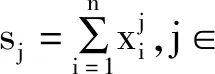
这就是著名的牛顿公式,详见文献[12-13]．由式(5)可得

首先,由(6)式不难解出σ1,σ2,…,σn-1．

如果可以确定σn,那么可以得到一个解为{(x1,x2,…,xn)}的一元n次方程xn-σ1xn-1+…+(-1)nσn=0,从而方程组(4)有唯一解(不计次序意义下)．而σn的取值和m与sm的取值密切相关．下面分情况讨论σn．

情况1若m=n,由(6)式容易解出唯一的σn,从而式(4)有唯一解(不计次序意义下)．

情况2若m>n,为了方便,令Δi=(-1)iσi,i=1,2,…,n．

1) 当n

因此方程组(4)有唯一解(不计次序意义下)当且仅当系数矩阵行列式