考虑司机偏好的城市轨道交通混合乘务轮转模型

潘寒川，戚博洋，胡华*，康磊，沙悦，刘志钢

(1.上海工程技术大学，城市轨道交通学院，上海 201600；2.上海磁浮交通发展有限公司，上海 201204)

0 引言

乘务计划在城市轨道交通的运营管理中扮演着重要的角色，它主要包括乘务排班计划和乘务轮班计划。乘务轮班计划作为乘务计划编制的核心环节，旨在合理安排乘务员的工作，确保城轨的运营有序进行。优秀的乘务轮班计划不仅需要合理安排司机任务，更应体现足够的人文关怀。

目前，国内外研究人员在乘务计划编制问题上已取得一定成果，绝大部分学者从乘务排班问题入手，对乘务员人数和乘务员利用率等方面进行研究，例如，胡汪源[1]将乘务排班问题归结为VRP 问题，设计时空网络对问题进行建模，并以减少乘务费用和间休时间为目标优化乘务排班问题。袁仁杰[2]将乘务排班问题和乘务指派问题分别转化为集合覆盖和运输指派问题，分别采用遗传算法和基于规则的启发式算法进行求解。侯彦娥等[3]针对我国公交车运营模式的特点，提出“人车绑定”模式下的公交司机排班模型，设计混合元启发算法解决了以往车辆和司机无法兼顾考虑的问题。刘昊翔等[4]和许仲豪等[5]采用列生成思想，结合深浅算法和贪婪算法，分别以车辆与司机运营总成本和司机工作效率为目标求解乘务排班计划。

相较于乘务排班计划，乘务轮班计划研究起步较晚，大部分成果均借鉴于航空和铁路，适用性较低。石俊刚等[6]重新思考城市轨道交通的轮转问题，设计优化模型，以最小化任务序列的广义费用为目标，来破解传统的固定轮转模式。SARJUT F.Z.等[7]建立多目标集合分割模型解决公交车车辆分配和乘务轮班协同优化问题，并设计多目标禁忌搜索算法进行求解。潘寒川等[8]基于客流峰差提出高峰系数概念，给出两种针对客流峰差而造成司机人数不均衡的乘务轮班计划编制方法。金华等[9]基于固定轮转模式构建乘务计划一体化优化模型，并改进列生成算法加快问题求解速度。ZHOU 等[10]设计多层时空网络图模型描述乘务排班和乘务轮转协同优化问题，尝试打乱传统“四班两运转”的轮转顺序，并采用基于拉格朗日松弛的启发式算法进行求解。FENG等[11]通过对偶分解理论将乘务排班和乘务轮转协同优化模型分解成一组独立子问题进行求解，求解质量较拉格朗日松弛算法有明显提高。戚博洋等[12]提出多出勤点多车场条件下影响司机工作效率和幸福度的轮休偏好、夜早连乘偏好及出勤点偏好，构建考虑司机偏好的城市轨道交通轮班计划优化模型。相关文献研究问题与本文研究问题对比请参考附录。

从以上研究可以发现，针对乘务轮班计划现有的研究成果大多仍是基于传统循环的轮转模式，即在给定的短周期内按照特定规律将任务安排给司机。同时，大部分研究的求解目标是从企业运营角度出发，在考虑司机偏好方面，将丰富等[13]的研究与本文研究进行对比，本质区别归纳为：①研究问题，相较于丰富等[13]考虑合理分配乘务员值乘和休息时间因素的乘务排班计划模型，本文主要考虑出勤点偏好和任务类型偏好的混合乘务轮班计划的新问题。②约束条件，本文考虑一些重要的实际约束，例如，任务唯一性约束和任务衔接约束。③求解方案，本文采用基于大规模领域搜索的模拟退火算法，相较于丰富等[13]采用遗传算法，本文所采用的算法确保算法的全局搜索能力，避免陷入局部最优解的情况。因此，本文提出城市轨道交通乘务混合轮转方案，并构建混合乘务轮转模型。本文具体贡献可归纳如下：

(1)本文提出了考虑司机偏好的城市轨道交通乘务混合轮转问题，将因峰差而产生的高峰任务纳入乘务轮班计划中，而非既有研究中传统的基础任务和高峰任务分别由不同班组的司机担任。根据本文提出的考虑司机偏好的混合轮转问题，根据司机的出勤点偏好和任务类型偏好可以确定司机的疲劳状态，再根据不同疲劳状态给司机分配不同的乘务任务，达到公平分配任务的目的。在实际应用中，混合轮转模式具有更高乘务任务安排灵活性，可以更好满足司机的个人偏好需求，也能应对因意外情况导致的计划变动。

(2)本文构建了网络图底层模型，通过定义一组节点和弧确定1 个周期内的乘务任务序列。结合混合乘务轮转方案扩展初始网络图，构建混合乘务轮转网络图模型。该方法能够将城市轨道交通乘务轮转问题转化为带约束的网络路径问题，仅需求得覆盖网络图中所有节点成本最小的路径即可得到乘务轮转问题的结果。

(3)提出了大规模领域搜索的模拟退火算法，相较于既有文献直接使用Cplex 求解器求解，本文根据乘务轮转问题的特点改进大领域搜索策略中的删除算子和修复算子。针对领域搜索容易陷入局部最优的问题，采用模拟退火策略扩大搜索范围，增强全局寻优能力。

1 问题描述与建模

1.1 混合乘务轮转方案

城市轨道交通为应对早晚高峰出现的客流不均衡现象，高峰期和平峰期之间通常会采用非等间隔运行图，但在同一时间，例如高峰期内，则采用等间隔运行图，便于运营组织和保持服务水平，节省运营成本。运行图上线列车数如图1 所示，Nm,Ne,Na分别表示早高峰，晚高峰和平峰时期上线列车的数量。单一循环轮转方案在应对此类运行图时通常需要的轮转司机人数较多，人员利用效率也较低。针对这一问题，很多学者提出采用“独立峰班”的方法灵活应对列车运行图变化，将司机分成基础班组和高峰班组。基础班组人数为平峰时期满足运营条件所需的最少司机人数，剩余人数则由高峰班组填补。基础班组按照单一循环模式轮转；高峰班组按照某一特定规则进行轮转。

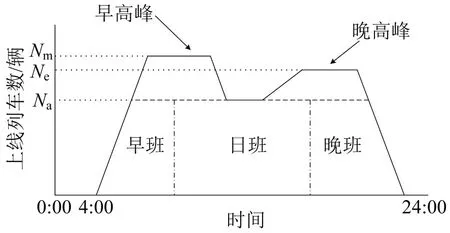
图1 分时段上线列车数量Fig.1 Diagram of train number on line in different periods

为进一步优化轮转机制，合理分配工作量，达到最大程度的任务均衡和节约成本，本文将高峰班组与基础班组的任务进行混合轮转的混合轮转制，提出混合乘务轮转方案。根据司机休息前累计驾驶时长和休息时长将司机划分为不同状态，为其安排后续的乘务任务。考虑到不同线路司机配备数量和线路条件不尽相同，提出以司机平均工作负荷代替传统轮转中的班制作为轮转的依据，司机平均工作负荷Wl为

式中：Tr为运行图总列车运行时间；cb为一个传统班制班组所需司机数量；cs为高峰班组当日值乘所需的司机数量；f为高峰班组工作时间系数，为高峰班组平均工作时间与传统班组平均工作时间的比值，通常取0.5。公式计算结果向下取整。

综上，混合乘务轮转方案如图2 所示，该图可被视为决策树，决策树的各个分支对应于在编制乘务轮班计划的过程中添加新的乘务任务时可能发生的所有情况，遵循哪个分支取决于司机值乘任务的实际情况。决策树的每个节点标有①、②、③或IMP的标签，分别对应当值乘前正在构建任务序列的司机的状态。其中，状态1表示司机处于标准状态；状态2表示司机处于有受限制的状态；状态3表示司机处于疲劳的状态。

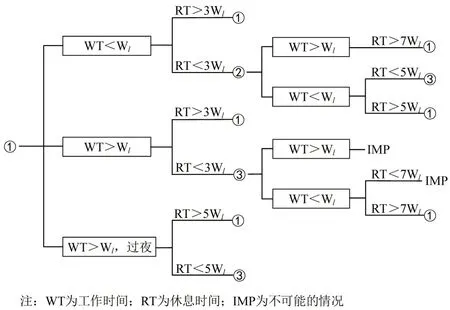
图2 混合乘务轮转决策树Fig.2 Task-type-mixed crew rostering decision tree based

从图2中可以看到，混合乘务轮转决策树图的决策过程如下：(1)当司机工作时间WT小于平均工作负荷Wl时，如果休息时间RT 大于3Wl，则司机处于标准状态；如果RT小于3Wl，司机处于轻度疲劳状态，则需要继续决策WT与Wl之间的关系。如果WT 大于Wl，则RT 大于7 倍Wl时，司机才能处于标准状态；如果WT 小于Wl，则RT 大于5 倍Wl时，司机才能处于标准状态，RT 小于5 倍Wl时，司机处于疲劳状态。(2)当司机工作时间WT 大于平均工作负荷Wl时，如果休息时间RT 大于3Wl，则司机处于标准状态；如果RT小于3Wl，司机处于疲劳状态，则需要继续决策WT与Wl之间的关系。如果WT 大于Wl，此时是不可能出现的情况；如果WT小于Wl，则RT大于7倍Wl时，司机才能处于标准状态，RT 小于7 倍Wl时，是不可能存在的情况。(3)当司机工作时间WT 大于平均工作负荷Wl，且工作过夜时，如果休息时间RT 大于5Wl，司机处于标准状态；如果休息时间RT 小于5Wl，司机处于疲劳状态。

根据上述轮转规则，构建网络图模型，如图3所示。模型的底层网络为基于连接的网络图模型，该初始网络图包含3 类节点，分别为源点、汇点和中间节点；源点和汇点分别表示任务序列的开始和结束，中间节点表示一个可被执行的乘务任务。中间节点之间由连乘弧进行连接，由源点出发的弧，称为源点弧，到达汇点的弧，称为汇点弧，则网络图中由源点出发，最终达到汇点的路径即为在该周期内的乘务任务序列。

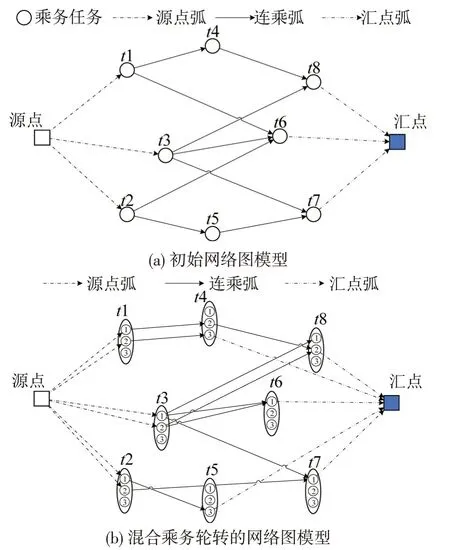
图3 网络图模型Fig.3 Diagram of network model

结合混合乘务轮转方案可将初始网络图进行扩展，构建混合乘务轮转网络图模型，该网络图中1 个乘务任务节点被扩展为3 个子节点，分别对应司机的3 种疲劳状态，例如，t1-①节点表示司机以状态1执行乘务任务t1，以此类推。

1.2 偏好设计

传统乘务任务轮转计划在编制时通常不会考虑司机的偏好，导致列车司机在值乘乘务任务时会产生不良情绪，影响工作质量，提高人为事故发生率，间接影响城市轨道交通运营安全。为弥补传统轮转计划在这方面的缺失，结合现场对司机调研结果和不同线路条件进行综合分析，将司机的偏好归纳为以下几条，且将符合司机偏好分配的乘务任务换算为一定量的奖励，用于抵消部分该乘务任务所属乘务任务序列的成本。

(1)任务类型偏好

司机任务类型的偏好定义为，工作时长超过司机平均工作负荷的乘务任务为长任务，反之，为短任务；需要在车场过夜的乘务任务为过夜任务，反之，为常规任务，如图4 所示。若乘务任务满足司机的某项偏好，产生ρa补偿成本，a表示为任务类型偏好。分配给司机k∈K的乘务任务序列i∈I中，所有乘务任务满足次任务类型偏好时，其总补偿成本为。由于轮转机制决策树中对长任务和过夜任务的休息时间做出了修正，所以，任务类型偏好不会对司机在整个乘务任务序列中的总工作时长产生影响，并不会影响工作量分配的均衡性。

图4 任务类型偏好Fig.4 Diagram of task type preference

(2)出勤点偏好

为方便管理，现代城市轨道交通线路会设置多个出勤点，司机可以根据自身条件选择1个或多个偏好的出勤点。如果分配给司机的乘务任务满足司机出勤点偏好，则会产生ρb的补偿成本，b表示为出勤点偏好。如图5 所示，对于出勤点偏好为A的司机，任务1的出勤点和退勤点均满足其出勤偏好，则产生的补偿成本为2ρb；而任务2仅退勤点满足其出勤偏好，则产生补偿成本为ρb。故分配给司机k∈K的乘务任务序列i∈I包含次满足出勤点偏好时，其总补偿成本为

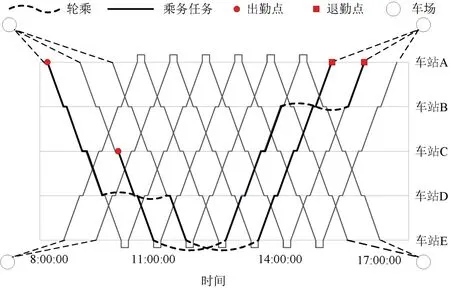
图5 出退勤点偏好Fig.5 Diagram of attendance point preference

为方便后续建模，此处，定义偏好类型集合θ={a,b}，则偏好产生的补偿成本可以表示为，其中，ϑ∈θ。

1.3 数学模型

在以往城市轨道交通乘务计划研究过程中，学者常用集合覆盖模型和集合分割模型建立乘务计划模型。考虑目前城市轨道交通运营时，所有乘务任务序列必须分配给司机，且常规的乘务任务不需要多名司机同时值乘1 个乘务任务序列，所以，本文采用集合分割模型建立乘务轮转模型，模型中用到的符号及其含义如表1所示。

表1 变量，参数及集合符号定义Table 1 Variable,parameter and set definition

乘务轮转模型目标函数为

式(2)表示模型最终目标为所生成乘务轮班计划的总成本最小，总成本包含乘务任务分配成本和任务衔接冗余时间两部分组成，前者用于满足司机偏好分配，后者约束了司机多余的休息时间，从而提高司机任务安排效率，减少使用司机人数。

根据乘务轮转问题的相关规定，乘务轮转模型约束包含任务唯一性约束，工作时长约束以及休息时长约束。

(1)任务唯一性约束

任务唯一性约束指乘务任务集合中的所有乘务任务均必须被分配给1名司机值乘，不能重复分配，也不能由2名司机同时值乘同一任务，即

(2)工作时长约束

工作时长约束指司机在1 个周期内的总工作时长不能超过国家法规及行业规定的相关要求，即

(3)休息时长约束

休息时长约束指司机在连续2 次乘务任务之间的休息时长必须大于最短休息时长，即

根据上述规则建立网络图后，将城市轨道交通乘务轮转问题转化为带约束的网络路径问题，仅需求得覆盖网络图中所有节点成本最小的路径即可得到乘务轮转问题的结果。则原问题中的决策变量xi,k和yi,j变为αi,s,k和，分别表示司机k是否访问乘务任务j的子乘务任务s，若是，则αi,s,k=1，反之，αi,s,k=0；乘务任务i的子乘务任务s和乘务任务j的子乘务任务t之间的弧是否被分配给司机k，若被分配，则，反之，则。且两类决策变量之间需满足的耦合关系为

则相应的原问题中目标函数可以转换为访问所有乘务任务的总成本最小，即

式中：Cbase为司机值乘该乘务任务序列的固定成本，用于约束值乘任务的司机数量；gi为乘务任务i的工作时间费用。目标函数实际意义与原问题目标函数相同。

式(3)和式(4)相应变为

式中：Ii,s为能与乘务任务i的子乘务任务s衔接的所有乘务任务的子乘务任务集合，Ii,s⊆I。

式(5)转换为网络图中弧的连接关系，若不满足式(5)最短休息时长约束，则网络图中的两点间不存在弧。

模型约束条件除了原问题中的约束外，增加网络图中的流平衡约束，司机人数约束，任务衔接约束和决策变量取值范围约束。流平衡约束指网络图中所有中间节点的子节点流入的流量和流出的流量均应该相等，即司机值乘完一个乘务任务后，应继续值乘后续任务或者结束该乘务任务序列。流平衡约束为

司机人数约束指网络图中，从源点流出的流量应小于等于可用流量，即同时值乘乘务任务的司机人数应小于等于可分配乘务任务的最大司机人数m。为方便计算，本文规定网络图的源点没有子节点，用上标0，1表示。总流量约束为

任务衔接约束为两任务衔接时的时间先后关系约束，则所构建的网络图中的弧均为有向弧。任务衔接约束为

式中：A为决策变量集合。

决策变量取值范围约束为模型中决策变量规定的取值范围，即

重构后的模型为0-1整数规划模型，即

模型决策变量和约束数量如表2所示，决策变量和约束的数量主要和轮转周期内的乘务任务总数、司机班组人数以及乘务任务可以衔接的任务数量有关。对于1 个拥有27 个任务和37 个司机，轮转周期为7 d的实际案例，网络图的节点数量为273个，决策变量的数量约为230000个，可见随着乘务计划编制规模不断增加，决策变量的数量会大大增加，导致模型的计算强度越来越大。

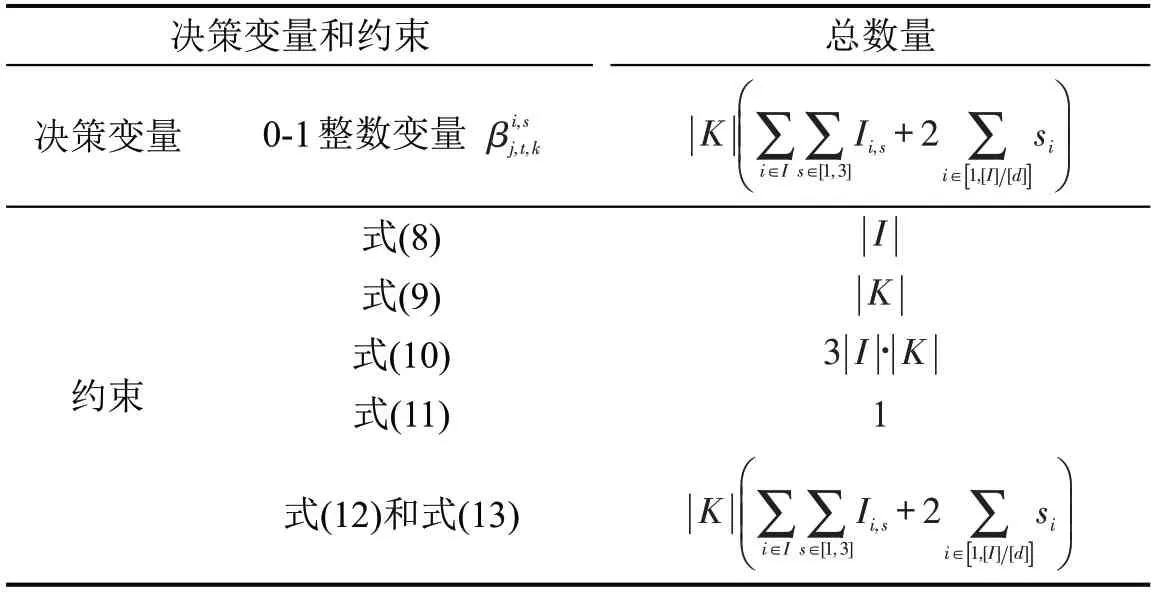
表2 模型相关决策变量及约束数量Table 2 Number of involved and constrains in the model

2 基于大规模领域搜索的模拟退火算法

针对建立的模型，本文设计大规模领域搜索模拟退火算法进行求解，并基于乘务序列的特点设计了多重删除算子，以提高算法的鲁棒性和全局寻优能力。本文采用自适应修复算子修复破坏后的乘务轮转计划，得到新的轮转计划。删除算子的实现过程是从方案路线中按照删除算子规则删除部分点，加入到删除集合当中。本文设计3 种破坏算子，并根据领域搜索结果的情况设计阶段删除策略，不断扩大规模领域搜索范围。

2.1 删除算子

(1)最差乘务任务序列删除算子

为确保司机一次出勤尽可能在满足轮转约束的情况下多值乘驾驶任务，该删除算子将选择平均值乘任务成本最高的1 名司机的乘务任务序列删除，并将该序列中所有任务添加入删除集合中，平均值乘任务成本为

(2)相关性删除算子

该算子通过计算任务之间的相关性，移除若干相关性最高的任务。本文计算当前乘务轮转计划中任务集合T1中的乘务任务与删除集合T2的关联度，选择关联度最大的若干个任务，将其从当前乘务轮转计划中移除，并添加入删除集合中。若删除任务后，导致任务序列断裂，无法连接，则根据删除后2个子序列的长度，选择长度较短的子序列一并删除，将子序列中所有的任务加入删除集合中，即

式中：ri,j为乘务任务i与乘务任务j之间的关联度；Ei为乘务任务i与删除集合T2的关联度。任务关联度包含3 部分，分别为任务衔接关系，两任务出勤点是否相同以及两任务的任务类型是否相同，取三者线性和的倒数作为两任务之间的关联度。则任务集合T1中的任务与删除集合T2的关联度为集合T1中的任务与集合T2中每个任务的平均关联度。

(3)随机删除算子

领域搜索策略搜索范围有限，搜索结果可能会陷入局部最优，因此，在删除算子中加入随机删除算子，增加优化结果的可能性，使搜索结果可以跳出局部最优情况。本文算法设计了3个删除阶段，3个阶段分别从(0,0.1]，(0.1,0.2]，(0.2,0.3]这3个区间中随机选择1个数，乘以当前解中乘务任务序列的总数作为阶段删除数，确保每个阶段有一定数量的乘务任务序列被破坏。

2.2 修复算子

(1)考虑成本的贪婪修复算子

该算子将被移除的乘务任务插入所有乘务序列中最好的一个位置，即插入以后带来的总成本增加最小。对每个乘务任务i计算插入到任务序列r的第j个任务和第j+1个任务中间的成本增量为

式中：Δzrj为任务i插入任务序列r的第j个任务后的成本增量；zrj为任务i插入任务序列r的第j个任务后的总成本；zr为任务序列r的初始成本。判断所有任务序列的所有位置，找到最佳插入位置。重复该步骤直到所有删除集合中的任务被插入，形成新的轮转计划。

(2)考虑成本带扰动的贪婪修复算子

该算子是对考虑成本贪婪修复算子的扩充，对于最优插入位置的成本增量给予一个扰动，然后，选取新成本增量最小的位置插入任务。重复该步骤直到所有删除集合中的任务被插入，形成新的轮转计划。在本算法中，每种修复算子的权重均会根据其产生新解的表现进行更新，每个算子的初始权重均为1，经过一定次数的迭代之后，需要更新一次权重，权重的更新式为

式中：ωd为某个修复算子的权重；sd为该算子的分数；ud为该算子被选中的次数；σ为权重系数。

每种算子初始得分均为0，在迭代时根据新解的表现更新得分，具体得分更新方式如表3所示。

表3 修复算子得分表Table 3 Table of repair operator score

3 案例分析

3.1 案例背景及参数

本文以上海市某条实际运营的城市轨道交通线路作为实际案例，该线路设39 座车站，3 个车辆段，线路走向为Y字形，全线设有3个出退勤点，工作日早晚高峰期间开行大小交路。在城市轨道交通系统中，每条线路存在多个车场和出退勤点，同时还需要应对工作日早晚高峰时段的峰班任务，增加了乘务轮班计划编制的复杂性，对运营效率和安全性产生了更加显著的影响，从而可以更好的验证优化模型的有效性。

乘务轮班计划包含任务号、任务类型、任务开始时间、任务结束时间、任务起点和任务终点等重要信息。这些信息将被整合使用，以确保乘务员的工作被合理安排，并最大程度地满足他们的偏好。乘务员偏好信息包括乘务员编号和乘务员偏好的出退勤点，如表4所示。

表4 乘务员偏好信息Table 4 Crew preference information

3.2 结果分析

选取不同规模的数据组进行案例分析，并和现场实际轮班计划进行比较，以验证本文提出模型的可行性与优劣性。所有数值实验均在8核3.2 GHz主频处理器，16 Gbytes的内存环境下进行，采用C#语言进行编程，数值实验结果及分析如下。

(1)出勤点偏好分配

本文模型和“独立峰班”模式下，乘务员不满足出勤点偏好出勤次数的对比情况如图6所示，本文模型在不同规模的数值实验中，不满足出勤点偏好的任务分配次数远远低于“独立峰班”的轮转模式，且本文模型的平均不满足出勤点偏好分配率为10.01%，基本满足司机能在自身偏好的出勤点进行任务出勤。

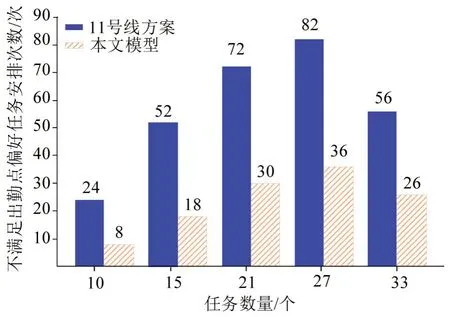
图6 本文模型与“独立峰班”模式下不满足出勤点偏好分配次数对比Fig.6 Comparison of not meeting attendance preference between model in this paper and independent peak shift

(2)任务类型偏好分配

本文模型和“独立峰班”模式下，乘务员不满足任务类型偏好出勤率的对比情况如图7所示，本文模型在不同规模的数值实验中平均不满足任务类型偏好分配率为37.85%，不满足任务类型偏好的任务分配率略低于传统“独立峰班”轮转模式的43.44%。这是由于参数设置时优先考虑司机对于出勤点的偏好，在满足出勤点偏好的基础上进一步满足司机对于任务类型的偏好，可以证明本文模型在任务类型偏好分配方面相较传统“独立峰班”模式具有一定的优势。

图7 本文模型与“独立峰班”模式下不满足任务类型偏好分配比例对比Fig.7 Comparison of not meeting task type preference between model in this paper and independent peak shift

(3)司机平均工作时长方差和对比

本文模型和“独立峰班”方案下，司机平均工作时长方差和的对比情况如图8所示，本文模型计算所得到的乘务轮班计划在工作时间的分配均衡性上优于“独立峰班”轮转模式，验证了本文提出的混合乘务轮转模式有效地均衡了司机的工作强度，避免司机出现工作量分配不均和疲劳驾驶的情况。

图8 本文模型与“独立峰班”模式下不满足任务类型偏好分配比例对比Fig.8 Comparison of variance sum of driver's working hours between model in this paper and independent peak shift

4 结论

本文以城市轨道交通乘务轮转问题为研究对象，提出混合乘务轮转方案。根据司机执行不同类型的乘务任务及执行完乘务任务后的休息时间区分司机的疲劳状态，并根据不同的疲劳状态分配给司机不同类型的任务。同时，为提高轮转方案的合理性，体现人文关怀，进一步考虑了司机的偏好需求，建立考虑司机偏好的城市轨道交通混合乘务轮转模型。通过实例验证，并与现场“独立峰班”轮转方案进行对比，结果表明：本文所建模型能够求解实际可行的乘务轮转方案，且相较“独立峰班”轮转方案，本文模型所求解的乘务轮班计划在司机使用人数和工作负荷分配均衡性方面更优。同时，本文模型更好地满足了司机对出勤点和任务类型的需求偏好，出勤点偏好满载率约为90%，任务类型偏好满足率超过65%。