城轨控流方案与列车开行频率及票价一体化优化方法

徐光明，卢春宇，钟林环，邓连波

(中南大学，交通运输工程学院，长沙 410075)

0 引言

目前，我国城市轨道交通的总运营里程和总客运量均居世界首位，但城轨系统有限的基础设施和运输能力与乘客出行需求的矛盾依然突出，部分线路的客流时空分布出现不均衡现象。线路部分站点乘客的候车时间长，车内拥挤程度高，同时，非高峰期运输能力利用水平低，企业运营效益和系统服务水平亟待提高。

为缓解线路客流高峰压力，提高运输服务水平和运营效益，当前研究主要针对城市轨道交通列车开行方案、城市轨道交通票价策略以及客流控制策略的优化展开。孙元广等[1]提出基于双层规划模型的城市轨道交通快慢车开行方案优化方法，上层模型以乘客出行时间和列车周转时间最小化为目标，下层模型设计考虑乘客换乘行为的客流分配方法。邓连波等[2]基于弹性需求建立双层规划模型，综合优化列车编组长度、列车开行对数以及列车开行时段。孙梦霞等[3]在轨道交通网络化运营条件下，优化线网中各线路发车间隔和各线路间发车时刻相位差，最小化企业运营成本和乘客广义出行成本。

在动态票价策略方面，LAN等[4]通过研究在台北实施的动态票价方案发现，地铁乘客对票价水平较为敏感，特别是对于高峰期收取附加费用。马铭遥等[5]针对北京地铁八通线的研究表明，实施城轨动态票价策略可以使高峰客流需求转移至低谷期，使峰谷差缩小35%。TANG等[6]在保证运营企业车票收入的基础上设计票价激励策略，缓解城轨站点排队拥堵和车内拥挤。值得说明的是，保证企业的票价收入对于票价策略的实施至关重要，例如，PERONE等[7]研究美国新泽西州实施的乘客非高峰期免费出行方案发现，实施该方案最终导致企业票价收入降低近25%，限于运营企业有限的资金，该方案因此被终止。

在客流控制策略方面，现有研究多结合列车开行方案和列车时刻表进行协同优化。孟凡婷等[8]从城轨系统优化角度出发，提出考虑跳停策略的城轨列车运行图与车站限流协同优化方法，最小化列车服务时间和乘车延误人数。卢亚菡等[9]研究考虑换入客流影响下的城轨列车时刻表与客流控制优化方法，最小化乘车延误人数。SHI 等[10]建立整数线性规划模型协同优化列车时刻表和客流控制策略，提高系统服务水平，降低运营风险。康崇仁等[11]针对客流过饱和条件下的地铁网络，提出客流控制策略与列车运行图协同优化方法，最小化乘客平均等待时间。

综合既有研究成果来看，协同优化城轨多时段客流控制方案、列车开行方案及票价方案的理论研究相对较少，并且，现有关于城轨客流控制方案的研究主要针对固定需求下乘客服务水平的优化，鲜有考虑控流方案对乘客出行选择行为和企业运营效益的影响。因此，本文提出城轨多时段控流方案与列车开行频率及票价一体化优化方法，其中，基于车站的控流方案制定各时段车站的允许上车人数。结合弹性需求描述一体化优化方案下乘客的出行费用和出行选择行为，最大化包括企业运营效益(企业票价收入与运营成本之差)和消费者剩余在内的社会福利。通过一体化优化方案实现多时段客流有效均衡及运力合理分配，提高运输服务水平并兼顾企业运营效益。设计嵌套Logit随机用户客流分配方法的遗传算法求解模型，基于南昌地铁一号线某工作日客流数据进行数值实验，验证模型与算法的适用性和有效性。

1 问题分析

1.1 符号定义

本文以贯通直线型城市轨道交通线路为研究对象，考虑线路单方向的高峰客流需求。记城市轨道交通线路为L={N,E}，N和E分别表示线路车站集和区间集，其中，N={1,2,…,n} 为按研究方向排序的车站集，n为车站总数。定义W为乘客出行需求的OD 对集合，(i,j)表示起点为i终点为j的OD对，(i,j)∈W且1 ≤i＜j≤n。

基于城市轨道交通客流需求在时间维度上的分布特点，将研究的城轨运营时间范围划分为若干个等长的运营时段。定义T={1,2,…,m} 为运营时段集合，m为时段总数，记每个运营时段的时长为Δt。为使优化方案与各时段出行需求特点相匹配，本文基于多时段研究城市轨道交通系统客流控制方案、列车开行频率及票价的一体化优化。

城市轨道交通一体化优化方案直接影响乘客在各时段的出行费用，进而影响不同时段内的客流出行需求。对于OD对(i,j)，将潜在出行需求记为Q(i,j)，弹性客流需求(实际客流需求)记为q(i,j)，时段t内的弹性客流需求记为。对于站点i，时段t内从该站出行的客流需求为

为便于模型构建，对本文的优化问题做出如下基本假设：

(1)城轨线路各OD 对之间的潜在客流需求已知且固定，不考虑乘客在本线与其他线路间的换乘行为。

(2)线路开行具有相同车型和编组数的列车，且所有列车均采取全线站站停的停站方式，以满足所有OD对的出行需求。

1.2 乘客广义出行费用

城市轨道交通乘客的出行时段选择直接受时段内广义出行费用的影响。给定列车区间运行时间和停站时间，乘客的广义出行费用包括4 部分：时段固定费用、车票费用、候车时间费用以及车内拥挤费用。

由于乘客选择在城轨系统各运营时段内出行的偏好程度不同，从而各时段内的客流出行需求存在差异，即产生时段固定费用。表达OD 对(i,j)在时段t内出行的固定费用，该费用体现客流需求的内在特征，受出行人群类别、出行者职业及出行者不同出行目的分布的影响，与出行客流量大小无直接联系。

一体化优化方案决策不同时段内的票价率，从而调控多时段客流需求。乘客的车票费用由OD基础票价与时段票价率决定，OD对(i,j)的乘客在时段t内出行的车票费用为

式中：ϑt为时段t内的票价率；F(i,j)为OD 对(i,j)的基础票价。

乘客的候车时间费用由在车站的候车时间量化表达。基于车站的城轨控流方案将根据时段内车站的客流需求和系统运能，制定各车站在每个时段允许的上车人数，优化运输能力配置，提高服务水平和运营效益。

时段t内列车在i站的剩余能力为

有别于WU 等[12]对乘客个体等待时间的精确计算，本文描述多时段控流方案下乘客选择在时段内出行的平均候车时间。乘客的平均候车时间与时段内的出行需求成正相关，与时段内乘客占用的列车运能成负相关。由于乘客占用的列车运能可能为0，故时段内的平均候车时间为

式中：α为站点乘客平均候车时间参数，一般取为0.5；M为足够大的正数，表示当乘客占用列车运能为0时，候车时间极大。

除了候车时间和票价费用，车内拥挤度也是影响乘客出行选择行为的重要因素。文献[13]发现，乘客在车厢内的感知拥挤度与乘客在车时间呈正相关的特点，因此，本文参考道路交通BPR 函数构建城市轨道交通车内拥挤度计算函数。在时段t内区间k的拥挤度为

综上所述，OD 对(i,j)的乘客在时段t内的广义出行费用为

式中：μ1、μ2为费用转换系数。

2 双层规划模型构建

基于对城市轨道交通运营企业和乘客双方利益的考虑，企业需根据乘客在各时段的出行需求特点制定相匹配的多时段一体化优化方案，最大限度的提高社会福利；乘客将根据制定的多时段一体化优化方案调整出行时段选择，使出行费用尽可能降低。因此，本文构建双层规划模型描述城轨系统中供需双方的相互作用，实现对城市轨道交通多时段客流控制方案、列车开行频率及票价水平的一体化优化。其中，上层模型以最大化社会福利为优化目标，以多时段列车开行频率、票价率及控流比为决策变量；下层模型描述一体化优化方案下乘客的出行选择行为，构建基于弹性需求的多时段随机客流分配模型，得到乘客选择在各时段的出行流量。

2.1 下层模型基于弹性需求的多时段随机客流分配模型

上层模型给定一体化优化方案，影响乘客在各时段的出行费用，进而影响乘客的出行选择行为。同一OD对的乘客根据各时段内出行费用的差异，可以选择在不同运营时段内出行。根据式(1)～式(7)计算乘客的出行费用，基于乘客在时段内的出行费用构建效用函数，采用Logit 模型刻画乘客的出行时段选择行为，OD对(i,j)的乘客选择在时段t内出行的概率为

式中：θ为将出行费用转换为效用的参数。

时段内的出行费用越低，则乘客选择在该时段内出行的概率越高。记为OD 对(i,j)的最小期望出行费用，即

基于弹性需求函数表达弹性客流需求与乘客广义出行费用之间的关系。OD 对(i,j)的弹性客流需求为

式中：η(i,j)为OD 对(i,j)的弹性系数，与其他存在竞争的交通方式(道路公共交通或网约车等)以及乘客的社会经济属性有关；弹性客流需求q(i,j)随着最小期望出行费用的增加而减少。

结合乘客出行时段选择的Logit 模型，OD 对(i,j)的乘客选择在时段t内出行的流量为

基于弹性需求的多时段随机客流分配模型可以构建为非线性互补问题(NCP)模型，即

2.2 上层模型一体化优化方案决策模型

基于城轨的定位和特征，运营企业在制定多时段一体化优化方案时应综合考虑企业效益和乘客服务水平，其中，以企业票价收入与维持列车正常运转所需的运营成本之差表示企业效益，以消费者剩余表示一体化优化方案所能提供的乘客服务水平。上层模型通过制定一体化优化方案(包括列车开行频率ft、票价率ϑt及站点控流比)最大化社会福利Z，包括企业运营效益Z1以及消费者剩余Z2。上层模型基于下层模型得到的出行流量计算相关指标，具体计算如下。

(1)企业运营效益Z1

企业运营效益等于票价收入与运营成本之差。票价收入由运营时间内所有乘客的票价费用组成；运营成本可表示为列车单位时间运营成本dt与运行时长τ的乘积，即

(2)消费者剩余Z2

消费者剩余是衡量消费者福利水平或系统服务水平的重要指标之一，在本文所构建的弹性需求函数形式下，表示为实际出行客流量q(i,j)与弹性系数η(i,j)之比[14]，即

因此，上层模型构建为

综上所述，城轨多时段控流方案与列车开行频率及票价一体化优化模型由式(1)～式(23)组成。其中，式(18)～式(23)组成上层模型，以最大化社会福利为目标，决策多时段控流方案、开行频率与票价率；式(1)～式(17)组成下层模型，描述一体化优化方案下乘客的出行选择行为，得到乘客的各时段出行流量。

3 算法设计

双层规划问题是典型的NP 难问题，一般根据问题和模型特点设计启发式算法求解。作为经典启发式算法之一的遗传算法通过模拟生物自然进化过程中染色体的交叉变异和选择过程搜索最优解，具有较强的适用性。现有关于列车开行方案和票价方案问题的研究常采用该算法求解。因此，针对本文模型特征，设计嵌套Logit 随机用户客流分配方法的遗传算法求解双层规划模型。首先，对上层模型中的列车开行频率、票价率及控流比变量进行编码；然后，通过解码规则将种群所有个体解码输入下层模型，使用Logit 随机用户客流分配方法得到给定一体化优化方案下的各时段乘客出行流量，并作为输入反馈给上层模型；通过上下层模型的反复迭代得到一体化优化方案。

3.1 Logit随机用户客流分配算法

输入：收敛精度ζ、最大迭代次数Ψ1；城市轨道交通线路{N,E}、运营时段集合T、OD对(i,j)的潜在客流需求Q(i,j)；乘客平均候车时间参数α、车内拥挤度参数β1和β2、列车额定载客人数C、额定载客系数ω、费用转换系数μ1和μ2、效用转换系数θ、弹性系数η(i,j)及目标函数权重系数ε。

输出：OD 对(i,j)的弹性需求q(i,j)，OD 对(i,j)在运营时段t内的出行需求。

Step 1 初始化

置迭代次数ψ1=0，初始化OD 对(i,j)的弹性需求q(i,j)=0，OD 对(i,j)在运营时段t内的出行需求=0。

Step 2 Logit随机用户均衡分配

根据式(1)～式(7)计算OD 对(i,j)在运营时段t内的出行费用

根据式(8)计算OD 对(i,j)的乘客选择在运营时段t内出行的比例

根据式(9)计算OD 对(i,j)的最小期望出行费用

根据式(10)计算OD 对(i,j)的弹性需求

根据式(11)计算OD对(i,j)的乘客选择在运营时段t内出行的需求

Step 3 基于相继平均算法更新流量

OD对(i,j)的弹性需求更新为

OD对(i,j)的乘客选择在运营时段t内的出行需求更新为

Step 4 收敛性检查

以式(26)判断各时段出行流量是否收敛，或算法是否达到最大迭代次数Ψ1。是，则停止运算；否则，令ψ1=ψ1+1，返回Step 2。

3.2 遗传算法

(1)编码及解码规则

编码规则：根据一体化优化方案中多时段列车开行频率ft、票价率ϑt及站点控流比变量的离散特征，对染色体采用0-1 二进制编码方式进行编码。

解码规则：利用区间占比解码各决策变量二进制字符串，得到对应十进制数值，转化式为

式中：ιj，κj，χj分别为开行频率基因、票价率基因及控流比基因对应二进制字符串。

(2)遗传算法流程

Step 1 初始化

置初始迭代次数ψ2=0，最大迭代次数Ψ2，种群规模Θ，染色体交叉和变异概率分别为Pc和Pm。根据式(21)～式(23)和编码规则随机生成Θ个染色体作为初始种群Φ0。

Step 2 计算染色体适应度

根据解码规则式(27)～式(29)得到解码后的一体化优化方案。计算适应度函数值，由于模型目标函数求最大化，本文直接将目标函数作为适应度计算函数。

Step 3 交叉操作

生成随机数δ∈(0,1)，若δ≤Pc，则进行交叉操作：从种群Φ(ψ2)中随机选择2 个染色体，随机交换2 个染色体的同位基因，得到2 个新的子代染色体，放入集合Φˉ(ψ2)。

Step 4 变异操作

生成随机数τ∈(0,1)，若τ≤Pm，则进行变异操作：随机选取种群Φ(ψ2)中个体的某些基因进行二进制0-1替换。若变异后的染色体不满足决策变量约束式(21)～式(23)，则对其进行调整，直至满足条件，调整后的染色体放入集合(ψ2)；若变异后的染色体满足相关约束，则直接放入集合(ψ2)。

Step 5 选择操作

执行轮盘赌选择操作，根据适应度大小从集合Φ(ψ2)∪(ψ2)中选出Θ个个体构成下一代种群Φ(ψ2+1) 。置ψ2=ψ2+1。

Step 6 终止条件判断

若ψ2＞Ψ2，停止计算，输出最优解；否则，转至Step 2。

4 算例分析

4.1 参数设置

为分析一体化优化方案与求解算法的有效性，以南昌市地铁一号线某工作日出行客流为基础进行算例分析。线路全长28.84 km，24 个车站，以双港站至瑶湖西站为研究的列车开行方向，对应站间区间以编号1～23 依次排序，线路站间距如表1 所示。基于客流的时间分布特征，以1 h 为时间间隔将线路运营时间范围7:00-10:00划分为3个运营时段，其中，时段2 为高峰时段。本文将换乘站的换入和换出客流视为乘客在本研究线路站点上的出行客流。参考陈治亚等[15]的参数设置，模型部分参数取值如表2所示。

表1 线路站间距Table 1 Station spacing

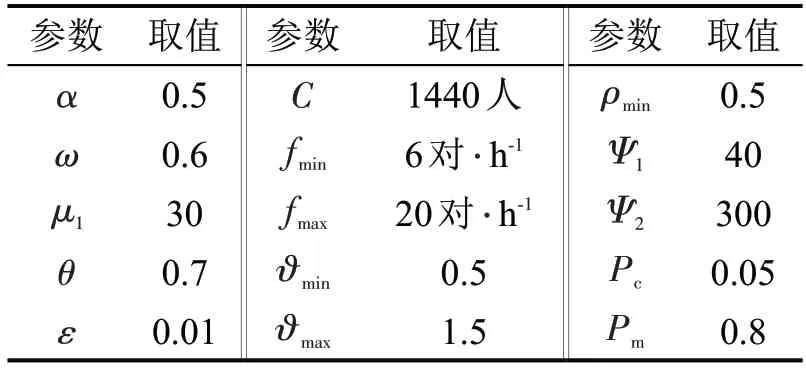
表2 参数设置Table 2 Parameter setting

4.2 优化结果分析

使用Visual Studio 2022 进行编程求解。各运营时段票价率和列车开行频率优化结果如表3 所示，对比优化前后不同运营时段客流分布情况，结果如图1所示。

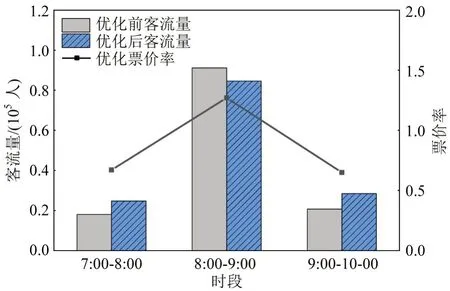
图1 各时段优化前后客流量对比Fig.1 Comparison of passenger flow before and after optimization in each period

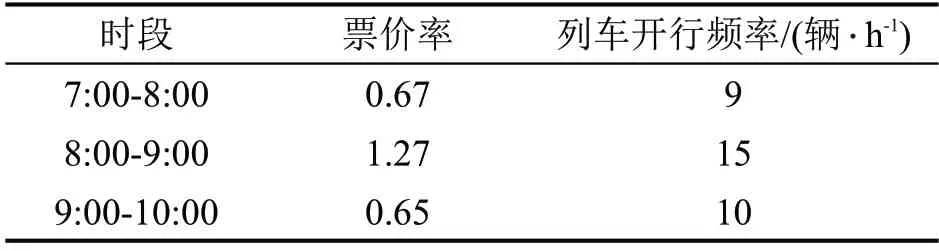
表3 各时段票价率与列车开行频率优化结果Table 3 Optimization results of fare rate and service frequency

由表3可知，优化后高峰时段2票价率为1.27，非高峰时段1 和时段3 票价率分别为0.67 和0.65。结合图1 可以看出，优化后，各运营时段内客流量增降情况与时段内票价率增降趋势相反。时段2票价率提升，使该时段部分潜在出行需求向其他低票价水平时段转移，该时段内客流量降低；时段1和时段3 则降低票价率吸引更多潜在客流需求出行，有效提高该时段内出行流量。由此可以看出，通过对线路票价水平进行调整，可以降低高峰时段客流需求，均衡其他时段客流量，缓解客流在时间层面分布不均衡的现象。同时，优化后，时段1和时段3 的列车开行频率由11 辆· h-1分别降低到9辆·h-1和10 辆·h-1，高峰时段2 的列车开行频率则保持15辆·h-1不变，以满足巨大的高峰客流需求。

对比优化前后各OD客流需求变化情况如图2和图3所示。

图2 原始情况各OD客流需求分布Fig.2 Original OD demand distribution

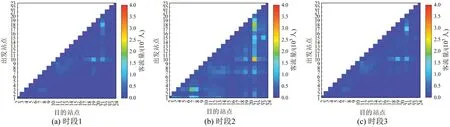
图3 实施一体化优化方案后各OD客流需求分布Fig.3 Distribution of OD demand after integrated optimization scheme

由图2 和图3 可知，各时段OD 客流量变化情况与时段内票价率变化趋势相反。优化后，时段2票价率提升，使该时段OD客流量降低；时段1和时段3 票价率降低，吸引更多客流需求。由此表明，优化城轨票价，可以降低各OD 高峰时段客流量；同时，吸引更多OD需求选择城市轨道交通非高峰期出行，满足更多客流需求。

线路站点各运营时段控流比优化结果如图4所示。

图4 各时段控流方案优化结果Fig.4 Optimization results of passenger flow control scheme

由图4 可知，时段1～时段3 的站点平均控流比分别为0.85、0.75 和0.88。由于选择在时段1 和时段3 出行的客流需求较少，优化后，时段1 和时段3的列车开行频率(运输能力)基本能满足客流需求，控流比较高，控流强度处于较低水平。相反，由于时段2为客流出行高峰时段，乘客对该时段内运输资源的竞争加剧，为避免上游车站乘客占用过多列车能力，导致后续车站部分乘客无法登车引发滞留现象，控流方案对高峰时段2内线路上游车站实施较高的控流强度，为中下游车站预留一定列车能力，优化列车运力使用。因此，对城轨线路实施控流方案能够更加合理地利用列车运输能力，优化系统运输能力在各站点的配置。

为进一步体现一体化优化方案下客流需求与列车运输能力间的关系，对比原始情况下和实施一体化优化方案后各时段区间断面需求与列车运输能力之比，如图5和图6所示。

图5 原始情况下区间断面需求与列车运输能力之比Fig.5 Ratio of original section demand and train capacity

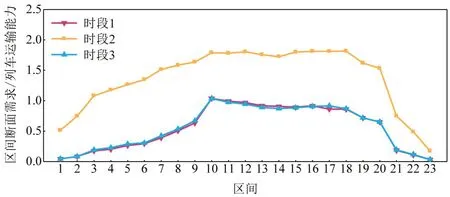
图6 实施一体化优化方案后区间断面需求与列车运输能力之比Fig.6 Ratio of section demand and train capacity after integrated optimization scheme

由图5可知，原始情况下，时段2的列车运输能力难以匹配巨大的高峰客流需求，区间5～区间20的断面客流需求均远大于时段内的列车运输能力；同时，时段1 和时段3 内的列车运输能力均大于各区间断面需求，列车运力利用水平较低，造成运输资源浪费。

由图6 可知，实施一体化优化方案后，高峰时段2的客流运输压力得到缓解，区间断面需求与列车运输能力之比的最大值由2.06 降低至1.81；同时，时段1和时段3的列车运力利用水平得到提升，列车运输能力基本匹配时段内的客流需求。

对求得的一体化优化方案与原始方案进行对比，结果如表4 所示。企业票价收入增加11.81%，企业运营成本降低8.11%，消费者剩余提升5.94%，目标函数值增加39.14%。对比优化前后结果可以看出：对城轨多时段票价率与列车开行频率及控流方案进行一体化优化，能够提高系统服务水平，吸引更多乘客选择城市轨道交通出行方式，有效提高企业票价收入和消费者剩余；同时，能够提升系统运输能力利用效率，降低企业运营成本。表明本文所提一体化优化方法能充分考虑企业和乘客的利益。

表4 优化方案与原始方案对比Table 4 Comparison between optimization scheme and original scheme

4.3 实施控流方案前后优化结果对比

城轨控流方案直接决定列车分配给各站点的运输能力，影响乘客的候车时间和车内拥挤费用，进而影响系统服务水平。为更好地体现城轨控流方案对乘客的影响，在优化得到的一体化优化方案中，通过保持优化后的票价率和列车开行频率不变，同时，将控流比设置为1，得到无控流方案下的乘客出行费用。对比实施控流方案前后乘客的平均候车时间和平均车内拥挤费用，如表5所示。

表5 实施控流方案前后平均费用对比Table 5 Comparison of average cost before and after passenger flow control

由表5 可知，通过实施控流方案，可以使乘客的平均候车时间由3.69 min降低至3.54 min，同时，可以使乘客的平均车内拥挤费用由5.07 元降低至4.86 元。因此，通过实施控流方案，优化列车运输能力在线路各站点的配置，可以在一定程度上降低乘客的候车时间和车内拥挤程度，提高系统运输服务水平。

为进一步说明控流方案对非高峰时段乘客车内拥挤费用的影响，结合图4～图6 进行说明。如图5所示，原始情况下，非高峰时段1和时段3的运输能力利用率较低，对比图6 可以看出，实施一体化优化方案后，非高峰时段1 和时段3 的列车开行频率由11辆·h-1分别降低至9辆·h-1和10辆·h-1，使企业运营成本降低；同时，运输能力利用水平得到提升，区间断面需求与列车运输能力之比的最大值为1.03，列车运输能力与客流需求基本匹配。但当客流需求接近运输能力时，车内拥挤程度急剧上升，乘客的拥挤感知成本显著增大。为缓解车内拥挤，如图4所示，在非高峰时段1和时段3对线路上游部分站点实施控流措施，为中下游站点乘客预留更多运输能力，可以降低乘客的车内拥挤程度。对比实施控流方案前后各时段平均车内拥挤费用变化情况，如表6所示。

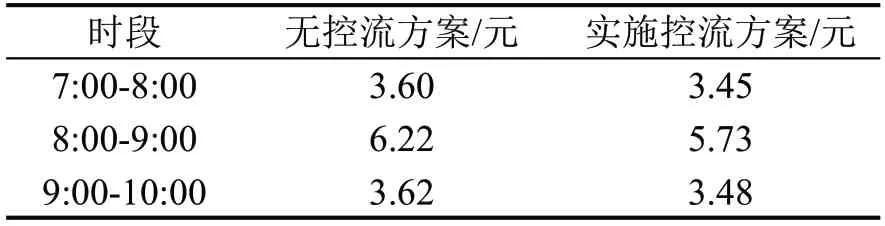
表6 实施控流方案前后各时段平均拥挤费用对比Table 6 Comparison of average congestion cost before and after passenger flow control

由表6可知，实施控流方案能够在一定程度上降低各时段乘客的平均拥挤费用。同时，以OD对(1,24)为例，该OD 在控流方案前后拥挤费用的变化情况如表7 所示，实施控流方案同样可以使该OD 各时段的拥挤费用降低。因此，在优化后的非高峰时段1 和时段3 的开行频率下，通过实施控流方案可以进一步优化运输能力在线路各站点的配置，同时达到降低企业运营成本并缓解车内拥挤程度的作用。

表7 实施控流方案前后OD对(1,24)拥挤费用对比Table 7 Comparison of congestion cost for OD pair(1,24)before and after passenger flow control

对比实施控流方案前后社会福利各项指标变化情况，如表8所示。

表8 实施控流方案前后优化效果对比Table 8 Comparison of optimization effect before and after passenger flow control

由表8 可知，相较于实施控流方案前，实施控流方案后，企业票价收入由8.24%提升至11.81%，消费者剩余由5.74%提高至5.94%，目标函数值由32.36%增加到39.14%。由此说明，在对城轨列车开行频率与票价率进行协同优化的基础上，进一步实施控流方案，可以降低乘客的平均候车时间和平均车内拥挤费用，提高运输服务水平，吸引更多客流需求选择城市轨道交通出行方式，同时，可以提高企业票价收入。因此，实施控流方案可以使企业和乘客的利益得到更好地兼顾，进一步提高社会福利水平。

5 结论

(1)提出一种城市轨道交通多时段控流方案与列车开行频率及票价一体化优化方法。分析一体化优化方案下乘客的出行费用和出行选择行为，基于不同运营时段内出行需求的差异性，设计多时段一体化优化方案，满足不同时段的客流需求。

(2)构建双层规划模型描述企业与乘客的相互作用，上层模型以最大化社会福利为优化目标，决策一体化优化方案，包括：控流方案、列车开行频率与票价率；下层模型为基于弹性需求的多时段随机客流分配模型，得到各时段的出行流量。设计嵌套Logit 随机用户客流分配方法的遗传算法求解模型。

(3)基于南昌地铁一号线进行算例分析。结果表明：城轨多时段控流方案与列车开行频率及票价一体化优化方法能够有效引导和吸引客流需求，降低高峰时段客流量，均衡不同时段内的出行需求。企业票价收入提高11.81%，消费者剩余提升5.94%；列车运输能力与各时段客流需求更加匹配，企业运营成本降低8.11%；实施城市轨道交通客流控制方案，可以优化系统运输资源在线路各站点的配置，降低乘客的平均候车时间和平均车内拥挤费用，进一步提高运输服务水平和企业效益。