考虑旅客跨楼中转的航空公司所属航站楼分配优化研究

李艳华，阳杰，刘志硕，邓杰

(北京交通大学，智慧民航发展研究中心，北京 100044)

0 引言

随着我国经济持续快速发展，机场航空业务量不断扩大。近年来，为满足高速增长的航空业务需求，新建航站楼或卫星厅，实行多航站楼运营，成为大型枢纽机场普遍采用的解决方案。枢纽机场是不同航线和不同航空公司，甚至不同交通方式的集结地，其核心是中转流程的管理。对于多航站楼的枢纽机场，由于不是每个航站楼均负责国际航班运行，中转的4种类型中最常见的国内转国际和国际转国内往往均涉及到跨航站楼的问题。尤其随着在不同航空公司之间中转旅客数量的快速增长，跨航站楼中转效率的提升成为强化枢纽机场中转功能的关键。

在多航站楼运营模式下，中转前后航班的航空公司可能位于不同航站楼，因此，存在一定数量的跨楼中转旅客。对旅客而言，相较于同楼中转，跨楼中转距离和时间通常更长，若航站楼之间被空侧相隔，往往还需花费额外的转运时间，导致中转流程最小衔接时间(Minimum Connecting Time,MCT)大幅增加，极大影响旅客的出行体验。对机场而言，则需根据跨楼中转旅客数量投入专门的人力及转运工具提供中转服务保障，由此产生额外运营成本。对于航空公司而言，通常希望机场尽量将同航系的航空公司(集团和下属控股/参股的航空公司，“同航系”)分配至同座航站楼，共享地面服务保障设施，提升航空公司的旅客中转体验，进而吸引更多的中转旅客。然而，考虑到航站楼运行容量限制，以及航站楼是否运行国际航班的局限性，严格的同航系位于同楼的分配方案可能无法满足。因此，如何科学合理地进行不同航站楼内航空公司的分配，最大程度满足航空公司的便利需求，在提升中转旅客出行体验的同时，促进航空公司协同运营和服务共享，提升机场中转水平，是机场亟待解决的问题。

目前，国内外学者从不同角度研究航站楼分配问题，但大多以航站楼功能分区和停机位分配的角度分配优化机场航站楼，关于枢纽机场多航站楼航空公司中转运营分配的研究还较少。航站楼功能分区研究方面，ZHANG 等[1]采用排队论模型优化安全流程，提出新的航站楼不同区域分工模式，达到最佳使用航站楼；马俊鹏[2]从扩大旅客量，提高旅客服务质量，提高人员和设备利用率等方面探讨枢纽机场航站楼功能分区问题；张佩浩等[3]利用Anylogic仿真软件的社会力模型，仿真优化分析机场航站楼值机区、安检区及候机区，从而优化航站楼功能分区。停机位分配方面，URSZULA 等[4]兼顾机场和航空公司双方利益，建立最大化鲁棒性、停机位利用率、航空公司机位偏好和最小化远机位航班量的多目标停机位分配模型；SENA 等[5]以旅客步行距离最小为目标建立机场停机位分配模型；ZHANG 等[6]以最小化实时飞行冲突、机滑行油耗和最大化登机桥率为优化目标建立停机位分配多目标优化模型，并提出一种基于余弦变异和自适应分组的改进束群算法求解模型；罗聿伦[7]以提升机场的运行效率，降低机场运行成本建立基于多目标差分进化算法的机场停机位分配模型。

在多航站楼航空公司运营分配的研究方面，目前国内外尚处于探索阶段，理论方面，SOCORRO等[8]从旅客福利和航空公司竞争的角度研究多航站楼航空公司分配方案对于机票价格的影响，提出在通常情况下，将航空公司分配至独立航站楼运营会削弱彼此的竞争程度，进而使票价增高；张彬等[9]归纳枢纽机场多航站楼的典型使用模式和航空公司运营分配基本原则，针对白云机场T1 和T2 航站楼，分别采用按联盟和以国内国际为主联盟为辅这两种方式进行分配，并分析方案优缺点；WU等[10]基于分析现有大型国际枢纽机场的案例，提出同联盟航空公司同楼运营可以为机场运营部门带来运行和经济效益的提升；邓海超[11]以国内外枢纽机场为案例，分类和总结多航站楼分工运营模式，并重点分析各种模式的优缺点及其影响因素。

以上学者在航站楼功能分区和停机位分配等方面进行了大量研究，但针对枢纽机场多航站楼航空公司中转运营分配的研究较少，多从多航站楼分工运营实例分析和运行经验的角度提出相关政策建议，侧重于定性分析，缺乏在多航站楼机场如何将各家航空公司合理分配至各个航站楼，以提高中转效率和减少跨楼中转问题上的研究。而且在实践方面，目前，机场在进行航空公司所属航站楼分配决策时多考虑航空公司联盟属性、航空公司自身属性(全服务和低成本)及航站楼分工属性(国际和国内)等因素进行决策，难以实现多主体利益兼顾。

基于此，本文以枢纽机场旅客跨楼中转的实际问题为背景，以多航站楼枢纽机场为研究对象，并基于多目标整数规划方法，研究以提升中转率为目标的枢纽机场多航站楼航空公司航站楼归属分配优化问题。从提升旅客中转便利性，促进同航系航空公司协同运营及降低机场运营成本的角度出发，以年跨楼中转旅客数量、同航系航空公司间跨楼中转组合数量、年旅客跨楼中转总时间和年跨楼中转国际/港澳台旅客数量最小为目标，构建多航站楼航空公司分配优化模型，并设计带模拟退火机制的自适应粒子群组合优化(Simulated Annealing-Adaptive Particle Swarm Optimization,SA-APSO)算法求解模型，同时，为各目标设置不同权重值对运营分配方案进行决策，进而提出多航站楼枢纽机场的航空公司归属航站楼优化分配方案，为实际工作提供理论依据和模型应用参考，以期大力提升我国枢纽机场建设，便利旅客中转出行。

1 航空公司所属航站楼分配优化模型构建

已知某枢纽机场航站楼(含卫星厅)的数量、各航站楼高峰小时旅客处理能力、各航空公司高峰旅客运输量及各航空公司之间相互中转旅客数量等，在保证满足航站楼旅客处理能力的限制下，将每家航空公司分配至1座航站楼，以满足优化目标的要求，从而得到合理的航空公司归属航站楼的优化分配方案。

1.1 模型假设

针对上述问题构建多航站楼航空公司分配优化模型。模型假设如下：

(1) 开通国际/港澳台航线的国内航司被分为国际/港澳台和国内这两部分，所有航司的国际/港澳台航线均分配至同一航站楼；

(2) 未开通国际/港澳台航线的航司，1 家航空公司能够且仅能被分配至1 座航站楼，且1 座航站楼至少分得1 家航空公司，开通国际/港澳台航线的航司，其所有国内航线也只能被分配至1座航站楼；

(3)不考虑登机口(到达口)的分配，假设航站楼内各登机口(到达口)中转至另一航站楼的所需时间相同；

(4)航空公司在成本既定的情况下，中转能提高后一航段的客座率；

(5)不考虑跨航司中转时旅客提取行李的时间。

1.2 模型建立

1.2.1 目标函数

分别以兼顾航空公司的便利需求，提升中转旅客的出行体验和降低机场运营成本的角度建立模型，对于航空公司而言，同航系航司分配在同一站楼，可以便利共享地面服务保障设施，节省航司服务成本，因此，设置同航系航空公司间跨楼数量最小的目标函数。对于旅客和机场而言，若跨楼中转人数和跨楼中转时间较大，导致MCT、机场人力和运力成本大幅增加，影响旅客中转体验，因此，设置跨楼中转旅客数量和年旅客跨楼中转总时间最小的目标函数，具体如下。

(1)目标1 年跨楼中转旅客数量最小

表示跨楼中转旅客数量越少，旅客满意度越高，该机场中转吸引力越大。

式中：C为航空公司集合，i,j∈C；S为航站楼集合，m,n∈S；xim和xjn为0-1决策变量，如果航空公司i或j被分配至航站楼m或n，则xim和xjn为1，否则，为0；Hij为从航空公司i中转至航空公司j的年旅客量；由于优化目标中涉及中转前后航班所属航空公司航站楼分配的决策，将出现2个决策变量的乘积，引入0-1 变量aijmn将模型线性化，当xim和xjn均为1时，取1，否则，为0。

(2)目标2 同航系航空公司间跨楼中转组合数量最小

表示同航系内部航空公司之间跨楼中转组合数量越小，同航系航空公司分配至同一座航站楼可能性越大，运营需求满足程度越高。

式中：yij为0-1变量，如果航空公司i和j属于同一航系时，为1，否则为0；引入0-1 变量bijmn将模型线性化，当xim、xjn及yij均为1时，取1，否则为0。

(3)目标3 年旅客跨楼中转总时间最小

表示旅客跨楼中转总时间最少，由于不同航站楼之间的跨楼中转时间不同，减少旅客跨楼中转总时间可以提高整个机场的跨楼中转效率。

式中：Dmn为从航站楼m中转至航站楼n所需的时间；Fijmn=Dmn·Hij为航站楼m中的航空公司i中转至航站楼n中的航空公司j的年旅客总中转时间。

(4)目标4 年跨楼国际/港澳台中转旅客数量最小

表示国际/港澳台跨楼中转旅客数量最少，包括国内转国际/港澳台和国际/港澳台转国内“(国际/港澳台中转”)，由于国际/港澳台中转相比于国内中转需要更繁琐的流程，若减少国际/港澳台跨楼中转旅客数量能一定程度提高机场中转效率。

式中：Gij为从航空公司i至航空公司j的年国际/港澳台中转旅客量。

1.2.2 约束条件

多航站楼航空公司分配优化模型的约束条件如下。

(1)航站楼旅客处理能力约束，即对任意航站楼，分配至该楼所有航空公司的高峰旅客运输量之和不得超过该航站楼高峰小时旅客处理能力(容量)。

式中：ci为航空公司i的高峰旅客运输量；ej为航站楼j高峰小时可保障旅客数量。

(2)航空公司分配航站楼唯一性约束，即除去国际航线被分配在国际航站楼的航司外，每家航空公司必须且仅能被分配至1座航站楼。

式中：Cd为除去国际航线的航司集合。

(3)航站楼航空公司数量约束，即每座航站楼至少分得1家航空公司。

(4)国际/港澳台航线分配航站楼约束，即开通国际/港澳台航线的航空公司其国际/港澳台航线部分只能分配至国际航站楼。

式中：CI为开通国际航线的航司集合；SI为国际/港澳台航站楼集合。

(5)变量关系约束。

2 求解算法设计

2.1 SA-APSO算法原理

传统粒子群优化(Particle Swarm Optimization,PSO)算法中，所有粒子通过追寻个体历史最优位置和全局粒子最优位置的方式进行探索，虽然可以进行快速的全局搜索，但是，容易导致搜索陷入局部最优[12]。基于上述问题，有学者改进PSO 算法，设计惯性权重和加速常数的动态更新，提出自适应粒子群优化(Adaptive Particle Swarm Optimization,APSO)算法，根据迭代情况动态调整粒子惯性权重等算法参数，提高算法的搜索性能和收敛速度[13]。APSO 在面对变量维度较高及局部搜索时有一定的局限性，而模拟退火(Simulated Annealing,SA)算法具有收敛速度快和在搜索时可以跳出局部搜索有效消除局部最优等特点[14]，因此，考虑将模拟退火机制引入自适应粒子群优化算法中，设计一种不仅全局搜索迅速而且局部搜索准确的模拟退火机制的自适应粒子群优化(SA-APSO)算法。

根据求解最小值问题的特点，在PSO算法中引入变动的惯性权重，对惯性权重根据迭代情况进行动态调整，使算法在迭代初期侧重全局搜索，后期侧重局部搜索。自适应惯性权重动态更新式为

由于在APSO算法后期侧重于局部搜索，粒子更新前后的位置容易一样，从而陷入局部最优解的概率增加，因此，引入模拟退火机制降低陷入局部最优解的概率。根据Metropolis准则，粒子迭代时，不仅接受优化解，还根据概率接受非优化解，即根据粒子迭代前后的适应度值变化量决定是否接受新的非优化解[15]。若在迭代过程中，粒子位置从U变化为V时，对应的适应度从p1变为p2，若p2＜p1，则认为粒子状态改变，即位置V被接受；若p2＞p1，则以一定的概率保持状态或改变状态，以保持位置U或接受位置V，Metropolis 准则认为位置V被接受的概率[16]为

式中：Tn、Tn-1为当前状态和上一状态模拟退火机制中的退火温度；K为退火速度常数，0＜K ＜1。

2.2 SA-APSO算法流程

(1)粒子编码

如同传统PSO算法，SA-APSO的粒子有二进制和实数等编码方式。实数编码意义明确，根据问题特点，本文采用实数编码方式。粒子用向量P表示，P=(xd1,xd2,…,xdi,vd1,…,vdi,xin1,xin2,…,xini,vin1,…,vini)，i为待分配航空公司数量，n为航站楼数量，xdi,xini∈{0,1,2,…,j,…,k}，xdi,xini=j表示第i家航空公司的国内航班或国际/港澳台航班被分配至航站楼j，若航司i在该机场无国内或国际/港澳台航班，则xdixini=0，vdi,vini分别代表粒子位置xdi,xini当前的速度。

(2)种群初始化

为避免种群在算法迭代过程中过早收敛，初代种群的多样性和代表性至关重要。随机生成h个范围在1～k之间的整数序列组成粒子，判断该粒子是否满足式(5)～式(14)的约束，若不满足，则重新生成；若满足，则与种群中已有粒子进行对比，若无重复，则将该粒子纳入至初始种群，若有重复，则重新生成。不断重复上述过程直至粒子数量达到预先设定的种群规模。

(3)计算粒子的个体最优值

根据建立的目标函数计算粒子的适应度值，并比较粒子当前的适应度值和历史适应度值，若当前值比最优历史适应度值更优，则将当前值设为pbest；当前值劣于最优历史适应度值时，引入模拟退火机制，通过式(16)和式(17)进行概率计算，决定最终是否接受当前值为pbest。

(4)计算群体最优值

将当前粒子的适应度值和全局最优适应度值gbest进行比较，若当前粒子适应度值优于gbest，则更新gbest为当前粒子适应度值；否则，不更新。

(5)粒子位置和速度更新

根据粒子群速度和位置更新式，并结合式(15)对所有粒子的速度和位置进行更新，若粒子有越界，则将其约束在边界边缘处。

(6)迭代结束

判断粒子群适应度变化值是否达到设置的精度或是否达到迭代次数要求，若未达到，则继续迭代；若达到，则停止迭代，输出最优解及最优适应度值。

3 算例仿真与分析

3.1 数据的选取与处理

选取我国西南地区某枢纽机场作为研究对象，该机场目前运营A和B两座航站楼，根据该机场官网可知，目前，A和B航站楼之间有免费摆渡车，运行时间为27 min，2023 年底，改扩建完成后将新增1座卫星厅C，与航站楼B之间通过捷运系统连接，所需时间为3 min，从A 航站楼中转至卫星厅C，需先前往航站楼B，再通过捷运系统前往卫星厅C，航站楼B 为国内和国际/港澳台合用航站楼，航站楼参数及各航站楼间中转时间如表1 和表2 所示，其中，航站楼面积及各航站楼间中转时间数据来源于机场运行管理部门，航站楼高峰小时旅客处理数量根据机场规划设计相关理论方法以航站楼建筑面积除以规划人均面积(国内旅客取值35 m2·人-1，国际/港澳台旅客取值45 m2·人-1)求得[17]，现行高峰小时旅客量由航站楼内各航司高峰小时旅客运输量求和所得，各航司高峰小时旅客运输量计算方法见下文。从表1可知，目前，航站楼B的运行已出现超容现象，故需增加卫星厅C 优化该航站楼航司分配。

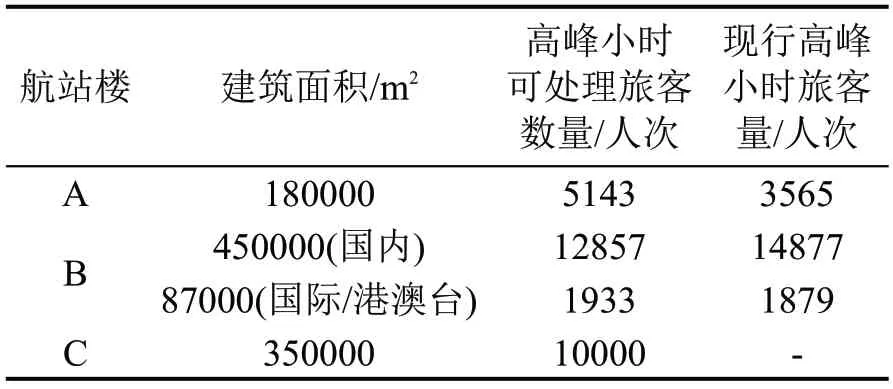
表1 航站楼参数Table 1 Terminal parameters

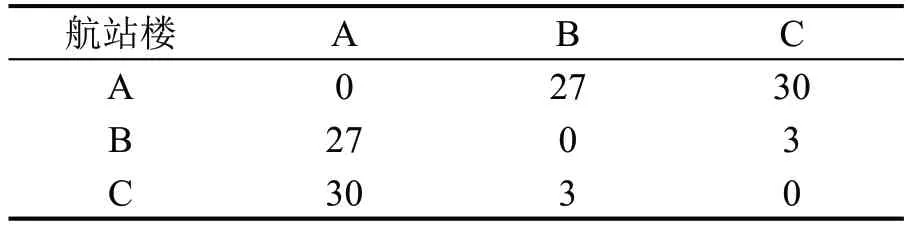
表2 各航站楼间中转时间Table 2 Transit time of each terminal (min)

该机场有国内外54家航空公司入驻，其中，各航空公司年旅客运输量数据来自于OAG(Official Airline Guide)数据库(2019年1月～12月)，航空公司之间年中转旅客数量来自于IATA(International Air Transport Association)数据库(2019 年1 月～12 月)，为计算各航司高峰小时旅客运输量，通过年旅客运输量分析OAG 旅客数据，该机场2019 年每月旅客运输量如图1(a)所示。选取旅客运输量最大的8月进行高峰小时旅客运输量计算，将每日航班以每小时为间隔划分为24 个时间段，分别计算2019年8 月每个时间段的日平均出港旅客和进港旅客量，如图1(b)所示，各航司每个时间段日平均出港旅客和进港旅客量如图1(c)和图1(d)所示。从图1 可知，两个高峰时间段分别为7:00-8:00 和20:00-21:00，通过OAG 数据计算这两个时间段的平均小时旅客运输量作为各航司高峰小时旅客运输量，如表3所示。

图1 西南某机场各航司高峰小时旅客运输量Fig.1 Peak hourly passenger traffic by airline division at an airport in southwest China

根据运营实际需求，算例仿真中，将该枢纽机场内航空公司航系分为：1国航系、2南航系、3东航系、4海航系、5其他和6国际及港澳台这6类。

3.2 模型与算法验证

为验证模型与算法的正确性和有效性，由于需要优化所有航空公司和航站楼，数据量大，模型复杂，故先选取小规模算例进行模型与算法验证，再应用于大规模的航站楼航空公司分配优化。以目前机场运行真实情况为基础，构建一个包含14 家航空公司和2 座航站楼的小规模算例。这些航空公司之间的年中转旅客量之和为282624 人次，占该机场年中转旅客总量的90%以上，具有代表性。

分别采用PSO、APSO和SA-APSO算法对模型进行单目标求解，通过多次实验迭代，分析对比各算法的求解效果以及本文改进算法的收敛性和稳定性。参数设置：迭代次数Gmax=200，种群规模N=50，学习因子c1=c2=2，惯性权重w=0.8，惯性权重最大值wmax=1.2，惯性权重最小值wmin=0.2，退火起始温度T=100 ℃，退火速度常数K=0.99。

应用各算法分别对模型目标Z1～Z4求解，结果如表4所示，表中“-”表示该航司在该机场未开通相应航班，各目标函数迭代曲线如图2所示。

图2 各目标函数迭代曲线Fig.2 Each objective function iteration curve

表4 小规模算例航空公司航站楼优化方案对比Table 4 Comparison of optimization schemes of airline terminal in small scale

由表4和图2可知，对于模型的求解，SA-APSO算法在收敛速度和求解效果上均较PSO 和APSO更优异，以目标函数1 年跨楼中转旅客数量为例，PSO和APSO优化后，年跨楼中转旅客数量分别下降了18.78%和24.21%，SA-APSO 算法优化后，年跨楼中转旅客数量下降了25.82%，优化效果更明显。分析SA-APSO 优化调整后的分配方案可知，优化后，同航系航司跨楼中转组合数量、旅客跨楼中转总时间和年跨楼中转国际/港澳台旅客数量降幅分别达到50%、25.82%和14.51%。由此可见，相较现行依靠经验进行的人工分配方案，利用本文提出的模型和算法进行优化的分配方案能够在中转旅客人数不变的基础上大幅减少跨航站楼中转旅客数量、同航系航空公司跨楼中转组合数量和旅客跨楼中转总时间，使同航系航空公司间集中运行程度提高，增加旅客舒适度和航空公司的满意度，促进机场中转服务水平的提升。实验结果充分验证了本文所提出的模型和算法的正确性和有效性。

SA-APSO算法的迭代过程可以分为以下几个阶段：第1 阶段，各目标函数值在经过20 次左右迭代后收敛，其原因是SA-APSO 算法收敛较快；第2阶段，目标函数值在第60～80次内震荡，其原因是模拟退火机制使粒子跳出局部最优解，寻找全局最优解；第3阶段，目标函数值在第90次后趋于稳定，表明该算法在本模型中达到最优解，证明了算法的收敛性。

为验证SA-APSO 算法的稳定性，对该算法整体运行100次，记录每次各目标函数的最优值变化如图3所示。

图3 各目标函数的最优值变化Fig.3 Change of optimal value of each objective function

由图3可知，经过100次的运算，各目标函数值均稳定在1 个区间内，其中，目标1 稳定在8401～8538，目标2保持为4，目标3稳定在222912～232768，目标4稳定在8296～8563，且各目标函数值的变化十分小，表明算法具有良好的稳定性。

3.3 实例应用

针对2023 年底卫星厅C 开通运行后航空公司航站楼分配方案的多目标决策实际问题，基于运营数据构建1 个包含54 家航空公司和3 座航站楼的大规模实例，使用SA-APSO 算法求解实例。算法参数设置如下：Gmax=200，N=50，c1=c2=2，wmax=1.2，wmin=0.2，T=100 ℃，K=0.99。

在求解模型前，采用线性加权法将多目标处理为单目标，并使用min-max 方法进行标准化，消除多目标之间数量级与量纲不一致带来的影响，由于本模型中目标z1、z3及z4相互之间变化情况影响密切，且随着不同航站楼分配方案的改变具有相同变化趋势，故假设以上3个目标权重相同，均为α1，目标z2值的变化情况与其他目标不同，故将其权重设置为α2，处理后的目标函数为

式中：z1max、z1min、z2max、z2min、z3max、z3min、z4max、z4min分别为目标函数z1、z2、z3、z4的最大和最小值，通过单目标优化得出；α2=1-3α1。

令权重α1在0.0～0.3 之间以0.05 为步长取值，在不同权重组合下，求得最优方案对应的目标函数值如图4所示。

图4 大规模算例中不同目标权重组合下的目标函数值Fig.4 Objective function value of different weight combinations in large scale example

由图4 可知，随着权重α1的增加，所得最优解对应的跨航站楼总中转旅客数量和国际/港澳台中转旅客数量及旅客跨楼中转总时间呈现下降趋势，同航系航空公司跨楼数量呈阶段性上升。根据计算结果，从图4中可以直观地反映出利益主体在两个目标之间权衡的过程，机场和航空公司可以根据自身发展现状及目标，根据图4确定最佳的α1和α2的取值。

选取4 个目标权重相等，即α1=α2=0.25 时，SA-APSO 求得最优解对应的分配方案进行分析，如表5所示。

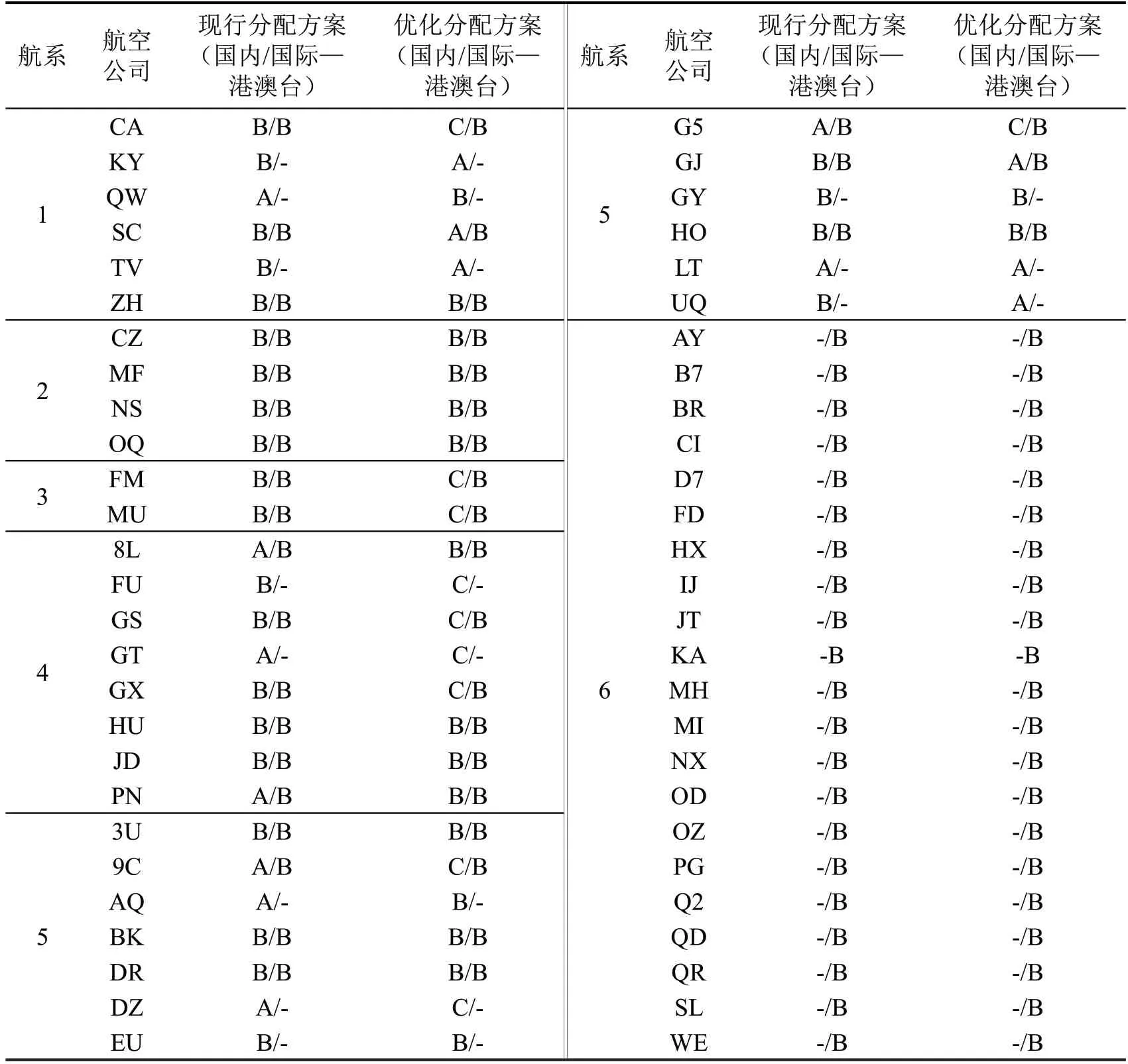
表5 实例中α1=0.25 时对应的分配结果Table 5 Allocation result when weight of α1=0.25 in real-life case

卫星厅C 增加前后分配方案的各目标函数值变化情况和航站楼容量使用情况，如表6 和图5所示。由图5(a)可知，现行分配方案中，航站楼B的运行已超出该航站楼的高峰小时处理能力，处于超负荷运行，因此，为缓解机场的旅客服务压力，该机场拟于2023年底投入运行1座卫星厅C。由图5(b)可知，在增加卫星厅C 后，各航站楼内航司高峰小时旅客运输量之和均低于航站楼高峰小时处理能力，极大程度降低了航站楼的运行负荷，提高了机场运行和中转效率。

图5 卫星厅C增加前后各航站楼容量使用情况Fig.5 Capacity utilization of each terminal before and after addition of satellite hall C

表6 卫星厅C增加前后各目标函数值Table 6 Objective function values before and after addition of satellite hall C

增加卫星厅C之前，由于航站楼B的国内区域已出现“超容”现象，故在增加卫星厅C 后，有部分航司从航站楼B调整至A或C，将会导致现行分配方案中可以在航站楼B 完成“国际/港澳台-国内”或“国内-国际/港澳台-国内”中转的航司需要进行跨楼中转，因此，不采取优化措施情况下，会增加跨楼中转旅客数量和跨楼航司数量。但根据表6 优化结果可以看出，卫星厅C 增加后“年跨楼中转旅客数量”和“年跨楼国际/港澳台中转旅客数量”较优化前分别下降了26.86%和28.84%；“同航系航空公司跨楼中转组合数量”较优化前下降了28.33%；“旅客跨楼中转总时间”较优化前大幅减少，降幅达89.91%。原本卫星厅C 增加以后跨楼中转旅客数会增加，但是，采用本文提出的优化模型和算法后，最小化目标函数值“跨楼中转旅客数量”“同航系航空公司间跨楼中转组合数量”等不仅没有增加，反而降低了。从而进一步验证了模型与算法的有效性。

由表5 可知，由于该机场新增卫星厅C 后，国际/港澳台航班仍在航站楼B运行，卫星厅C仅供国内航线使用，故各航司的国际航线分配方案并未发生改变，对于国内航线而言，有18个航司改变了航站楼，其中，QW、8L、PN及AQ这4家航司从航站楼A转移到航站楼B，KY、TV、GJ及UQ这4家航司从航站楼B转移到航站楼A，另外，CA、FM、MU、FU、GS、GT、GX、9C、DZ 及G5 这10 家航司从航站楼A和B转移到新建卫星厅C运营，为进一步分析优化前后各航司分配方案的变化情况，根据表1 和表3数据及上述优化结果，分析卫星厅C增加前后各航站楼航系分布情况，如图6所示。

图6 卫星厅C增加前后各航站楼航系分布情况Fig.6 Distribution of airline systems in each terminal before and after addition of satellite hall C

由图6(a)可知，现行方案中，国内航司的国内航线，仅有东航系和南航系是同一航系所有航司在同一航站楼，其他航系均分布在2 个航站楼，同航系需跨楼中转的航司组合达到120 个，但由图6(b)可知，增加C 后的航司分配方案中，虽然所有航司在同一航站楼的航系较优化前无变化，但东航系国内航线从航站楼B 转移到卫星厅C，整体而言，各航站楼内运行的航系数量较优化前少，且优化后同航系需跨楼中转的航司组合减少至86 个，从而促进了同航系航空公司的协同运营。

机场中转旅客可以分为国内中转和国际/港澳台中转两类，根据优化结果，计算增加C 前后各航站楼之间国内和国际/港澳台年跨楼中转旅客数量对比情况，如图7所示。

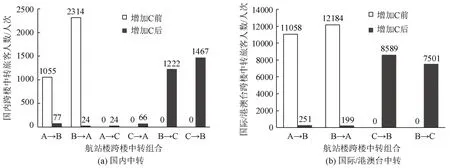
图7 卫星厅C增加前后各航站楼之间跨楼中转旅客数量Fig.7 Number of cross-floor transit passengers between terminals before and after addition of satellite hall C

由图7 可知，整体而言，国际/港澳台跨楼中转旅客数量远高于国内跨楼中转旅客数量，且增加C后，整体跨楼中转旅客人数较优化前低，优化前由于只有2个航站楼，故无跨楼中转旅客只集中于航站楼A和B之间。增加C后，由于卫星厅C与航站楼B 之间的中转时间远低于航站楼A 和B 之间的中转时间，故无论是国内还是国际/港澳台跨楼中转旅客均集中于航站楼B和卫星厅C之间，在减少了总跨楼中转人数的同时，大幅度缩减了跨楼中转时间，可以提高整个机场的跨楼中转效率，改善旅客的中转体验。

为进一步研究减少的跨楼中转旅客在航站楼的分布情况，分析不同中转模式下的跨楼中转情况，由于本算例中机场所有国际/港澳台航线均在同一航站楼，故无需研究国际转国际的跨楼中转模式，故将跨楼中转进一步分为国内转国内、国内转国际/港澳台和国际/港澳台转国内这3 种模式，根据优化结果计算增加C前后整体及3种不同模式下跨楼中转人数最高的10个航司组合及其跨楼中转旅客数量，如图8所示。

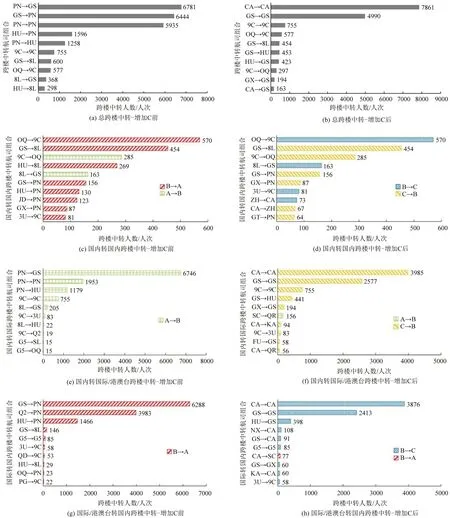
图8 不同模式跨楼中转人数最高的航司组合及其跨楼中转旅客数量Fig.8 Combination of airlines with the highest number of inter-floor transfers by mode and their number of inter-floor transfer passengers

由图8(a)和图8(b)可知，增加C后，航司组合的跨楼中转旅客数量较优化前显著下降，增加C前跨楼中转旅客数量较高的航司组合在优化后均被分配到了同一航站楼，增加C 后，跨楼中转旅客数量较高的航司组合中，CA、GS和9C是由于同一航司的国内和国际/港澳台航线不在同一航站楼，导致航司内部国际/港澳台跨楼中转旅客数量较多，但整体而言，增加C后的跨楼中转旅客数量较增加C前下降明显。对于3种不同模式下跨楼中转而言，由图8(c)～图8(h)可知，增加C 前3 种模式下，跨楼中转旅客数量较高的航司组合大多在增加C 后被分配至同一航站楼，因此，3种模式优化后的跨楼中转人数均较增加C前有所降低，且优化后在各种模式跨楼中转人数前10 的航司组合中，仅有国内转国际的SC 转QR 和国际转国内的CA 转SC 发生航站楼A和B之间，大多数跨楼中转均发生在航站楼B和卫星厅C之间。

上述研究结果表明，将改进的SA-APSO 算法用于求解本文建立的航空公司所属航站楼分配优化模型，可以在保证机场中转量不变且航站楼数量新增的情况下，有效降低跨楼中转旅客数量，减少旅客跨楼中转时间，同时，尽可能将同航系航空公司集中于同一航站楼，使航空公司协同运营和服务共享，最大限度减少资源浪费。同时，为每个目标设置不同权重值，可以综合考虑多方利益的权衡，得到灵活多样的解决方案，机场和航空公司可以根据上述实例仿真结果，基于对不同目标的侧重，协商确定各个目标权重，得出对应权重组合下的最优解，进而科学合理地制定该机场卫星厅C开通运行后的航空公司航站楼分配实施方案。

未来，随着枢纽机场的旅客运输量、中转人数及航司数量等的变化，在已知航站楼的数量、各航站楼高峰小时旅客处理能力、各航空公司高峰旅客运输量及各航空公司之间相互中转旅客数量等前提下，可以通过上述已得到验证的模型及算法对航空公司所属航站楼的分配方案进行分配和优化。

4 结论

本文以多航站楼枢纽机场为研究对象，提出以提升枢纽机场中转水平为目标的航空公司航站楼归属分配问题，建立了航站楼分配优化模型，并设计优化算法求解模型。

(1)以年跨楼中转旅客数量最小，同航系航空公司跨楼中转组合数量最小，年旅客跨楼中转总时间最小和年跨楼国际/港澳台中转旅客数量最小为目标函数，以航站楼容量限制和航空公司旅客处理能力限制等为约束条件，建立了多航站楼航空公司分配优化多目标整数规划模型，并设计了SAAPSO算法求解模型。

(2) 分别使用PSO、APSO 和SA-APSO 求解西南地区某枢纽机场小规模算例，结果表明，SAAPSO 求解效果最优，优化方案中4 个目标函数值降幅分别为25.82%，50.00%，25.82%和14.51%，验证了模型与算法的正确性和有效性；对算法整体运行100次，得出每次各目标函数的最优值变化幅度较小，验证了算法的稳定性；针对该机场改扩建后运行情况构建大规模算例，使用SA-APSO求解，得到不同目标权重组合的最优分配方案，机场和航空公司可以在此基础上根据各自侧重点进一步进行选择，综合确定最终实施方案。研究结果表明：本文提出的模型和方法能够为枢纽机场航空公司航站楼分配方案的制定提供理论依据与决策参考，具有重要实用价值。