基于强化学习的干扰条件下高速铁路时刻表调整研究

庞子帅，王丽雯，彭其渊*,b

(西南交通大学，a.交通运输与物流学院；b.综合交通运输国家地方联合工程实验室，成都 611756)

0 引言

研究高速铁路干扰条件下列车时刻表调整方法，一方面，可以缓解列车运行冲突，使铁路网络通过能力快速恢复，保证铁路运输的安全运营；另一方面，可以提升高速铁路调度决策水平，有效地减少我国高速铁路网络列车和旅客晚点时间，对提升高速铁路的运输效率与旅客的出行服务质量具有重要作用。

干扰条件下，列车时刻表调整的既有研究主要基于仿真方法、数学优化方法和强化学习方法。仿真方法的优势在于能够提供一个精确、可靠及直观的系统评估平台。朱子轩等[1]运用多智能体通信机制，建立单线铁路网络列车运行智能调度仿真模型，利用Anylogic软件将仿真模型运用于西南地区某单线铁路网络，验证模型的有效性及合理性；杨锐等[2]基于部件组合思想，同时，考虑线路可双向运行和列车运行过程中随机扰动，建立列车运行仿真模型，可快速生成与列车运行环境和列车运行规则对应的仿真框架；QUAGLIETTA等[3]研究随机干扰条件下最优调度方案的稳定性问题，开发将调度系统与仿真环境结合的框架，通过评估不同预测水平下的干扰情景，探讨预测范围对稳定性和交通管理效果的影响。数学优化方法主要根据列车运行资源占用情况设定约束条件(例如，到发线最大数量限制、区间最小运行时间限制及最小间隔时间限制等)实现制定目标。VEELENTURF等[4]建立整数线性规划模型，模型考虑干扰开始阶段至恢复正常阶段的铁路网络信息，测试结果表明，模型能够在较短的计算时间内找到最优解；邓念等[5]针对高速铁路区间完全中断情况，构建列车运行调整混合整数线性规划模型，模型旨在尽量减少取消列车的数量和列车晚点时间加权求和量；徐培娟等[6]基于替代图理论，针对多种干扰事件建立混合整数线性优化模型，模型可同步实现列车运行调整和列车运行径路调整，通过两阶段近似求解算法在600 s 内可以实现求解；李智等[7]研究多条线路列车运行图对抗干扰的鲁棒性，引入经济学中的边际效用递减规律优化列车缓冲时间，提升时刻表鲁棒性；牛宏侠等[8]基于生灭过程提出能够将车站和区间冗余时间同步优化的模型，模型可以平衡冗余时间不足和双重冗余之间的关系。随着大数据及云计算技术的发展，深度强化学习等人工智能技术逐渐被运用到列车运行调整中，基于人工智能的强化学习模型可以离线学习且无需多次求解。ŠEMROV 等[9]于2016年，最早将强化学习运用到列车时刻表调整上，但其仅使用Q-Learning算法，存在作用的维度限制和缓慢的收敛速度等缺点；LIAO 等[10]基于深度强化学习模型，研究干扰条件下考虑列车节能的时刻表调整方法，结果显示，提出的模型可以节约6%的能耗，但其未考虑列车区间和车站现场实际需求；代学武等[11]提出一种适用于突发事件下列车群运行调整的无模型强化学习方法，该研究可使列车群的平均晚点时间减少2%～20%；王荣笙等[12]提出干扰场景下基于蒙特卡罗树搜索-强化学习的列车运行智能调整策略优化方法，与通过CPLEX 软件求解的数学优化模型相比，提出的方法能在0.001 s内给出同样最优的列车运行调整方案；韩忻辰等[13]基于Q-Learning 算法研究晚点列车调整方法；俞胜平等[14]随后证明了策略梯度强化学习方法相比于QLearning算法有更好的效果。

目前，既有的研究方法中，仿真方法虽结果直观，但存在参数不确定、环境复杂和计算时间长等缺点。数学优化方法在大规模问题上面临求解效率低等问题。近年来，强化学习方法开始在列车时刻表调整中崭露头角，但大多仅基于Q-Learning算法。鉴于此，本文基于近端策略优化(PPO)方法，建立列车时刻表调整模型，得到以总晚点最小的列车时刻表调整方案。提出的模型可离线训练，无需在线实时求解，为铁路调度指挥决策模型的实用奠定基础。

1 问题描述

高速铁路列车在没有干扰的情况下需按照铁路部门制定的计划运行图运行。然而，铁路是一个复杂的系统，不可避免地受到内部基础设施、外部环境和人为因素的影响。在日常作业中，因线路故障、信号系统故障、异物侵入、列车车底故障及天气因素等突发干扰导致列车晚点是铁路运输组织中的常态问题。干扰条件下，铁路时刻表调整问题如图1 所示。图1(a)为铁路列车计划时刻表，包含4个车站(车站A、车站B、车站C及车站D)和4列列车(列车1、列车2、列车3 及列车4)。图1(b)为图1(a)对应的在2次干扰条件下可能的列车时刻表调整方案。干扰条件下，铁路列车调度员可采取，例如，改变列车区间运行时间、车站停站时间和运行顺序等方法调整得到实时的铁路列车时刻表。如图1(b)所示的实时时刻表中，对列车2 在车站A采取延长停站时间措施，避免与列车1的出站进路冲突；对列车1在车站A-车站B区间采取延长区间运行时间方法，避免在干扰发生时进入干扰区间；对列车1和列车2在车站B采取改变运行顺序的措施，减少总的列车晚点时间。

图1 干扰条件下列车时刻表调整示意图Fig.1 Train timetable rescheduling under interruptions

目前，干扰条件下，铁路时刻表调整的主要方法是基于人工调整，一方面，这种方式的前瞻性较差，且不同调度人员采取的调整策略和效果也各不相同；另一方面，数学优化模型在求解速度方面会随问题规模呈指数增长(例如受影响的晚点列车数)，而干扰条件下，需要铁路管理者能够快速决策，保障良好的运输态势。因此，传统方法难以满足铁路实时决策需求。本文使用深度强化学习PPO模型研究干扰条件下列车时刻表调整，并证明PPO 模型相对于既有强化学习和调度员现场决策方案具有明显优势，为干扰条件下列车时刻表调整决策奠定基础。

2 模型与算法介绍

2.1 深度强化学习模型

深度强化学习(Deep Reinforcement Learning,DRL) 模型主要包括智能体(agent)、环境(environment)、状态(S)、行动(A)和奖励(R)。强化学习的核心思想就是下一步的状态只和当前的状态以及当前状态将要采取的动作有关。智能体执行某一动作a(a∈A)将会影响环境状态，环境将由原来的状态s转换到新状态s′(s,s′∈S)，并且将为新状态环境给出奖励信号r(r∈R)，环境状态之间的转换是一个马尔科夫过程。随后，智能体基于来自环境的新状态和奖励反馈，根据特定策略执行新的动作。上述过程是智能体和环境通过状态、动作和奖励进行交互的一种方式。智能体贪婪地遍历每种动作，根据执行不同动作后环境给与相应奖励，后续将以大概率选取奖励回报高的动作执行，不断优化选取动作的策略，达到系统优化的目的。

本文建立的列车运行仿真环境包含列车运行车站和线路等基本信息，最小到发间隔时间信息等；智能体的动作空间包括改变列车区间运行时间、车站停站时间和运行顺序等；系统回报考虑列车在终点站的总晚点时间值；此外，系统每一时刻的环境状态作为输入，智能体根据输入决定采取的动作。最终，智能体根据各动作所得到的回报选取最优动作，最优动作序列构成铁路时刻表调整策略。模型结构框架如图2所示。

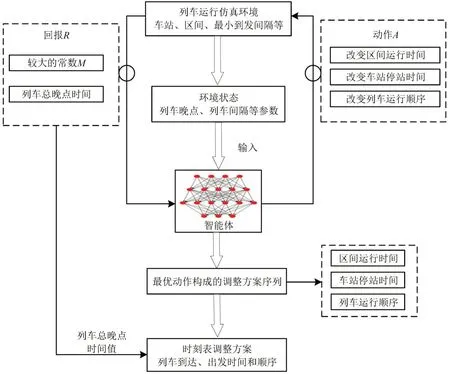
图2 模型框架图Fig.2 Framework of proposed model

本文使用近端策略优化(PPO)算法[15]。PPO 算法由OpenAI 于2017 年提出，被认为是目前强化学习中最先进的算法之一。其伪代码如下所示。

注：πθ 为策略；p 为转移概率。

2.2 DRL 模型策略

DRL模型使用神经网络模型当作其策略，使其可以对任何状态做出动作。本文使用执行者-评论家(Actor-Critic)模式的神经网络策略。执行者-评论家有两个网络：执行者和评论家。执行者输入是系统当前的状态，输出是各个动作对应的概率。执行者根据系统当前的状态决定应该采取哪个动作；列车运行仿真时，智能体在每一时间步都将以较大概率选择回报最大的动作执行，并以较小的概率选择其他动作，以探索不同的可能性。评论家输入是系统的状态和动作，输出是该动作的状态价值函数。评论家告诉执行者这个动作有多好，应该如何调整。执行者的学习是基于策略梯度方法。

对于执行者网络，最后一层使用SoftMax 函数输出各动作对应的概率，在不断学习过程中，更新执行者权重和误差项参数，调整各动作对应的选择概率；对于评论家网络，最后一层使用线性激活函数输出状态价值函数，输出为连续值，评估所选动作与预估回报之间的差异。执行者和评论家网络如图3 所示，其中执行者的输出维度L表示列车数量。

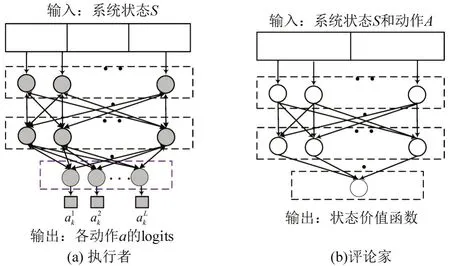
图3 执行者和评论家网络结构Fig.3 Structure of actor and critic

3 DRL模型实施

3.1 列车运行仿真环境和约束条件

本文建立的高速铁路列车运行仿真环境如图4所示。仿真环境的主要参数包括：车站数、车站股道数、区间里程、区间最小运行时间及最小到达和出发间隔时间。仿真环境包含个车站的一段区段={1,2,…,K}。该区段任意区间均可能发生随机干扰，列车在干扰发生期间不能通过。由于高速铁路上下行方向列车运行相互独立，本文将分开考虑上下行方向列车。线路各车站单方向可用到发线数量为ui,i∈{1,2,…,K}。受干扰影响的列车群需在满足约束条件的基础上运行到车站K。列车区间最小运行时间τi,i∈{1,2,…,K-1} 由铁路技术文件确定，列车停站最小停站时间为Wmin，列车最小到达和出发间隔时间分别为和。

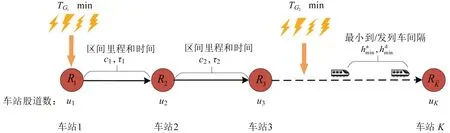
图4 列车运行环境Fig.4 Train operation environment

为保证得到的列车时刻表的可行性，系统仿真过程中需考虑列车运行约束条件。本文在列车运行仿真环境中考虑的约束条件如下。

(1)列车间隔约束

相邻两列车在到达车站时，间隔时间需满足最小到达间隔时间，出站时需满足最小出发间隔时间，即

(2)区间运行时间和车站停站时间约束

列车在区间运行时，运行时间需不小于最小区间运行时间。在车站停站时，停站时间应不小于最小停站时间，即

式中：Rmin和Wmin分别为区间最小运行时间和车站最小停站时间。

(3)车站到发线数量约束

为能够实现列车越行，在各车站越行时，同时停车的数量应不大于到发线数量，即

(4)列车发车时间约束

由于旅客上车的需要，列车只允许早到，不允许提前出发，即

对于区间运行时间和车站停站时间约束，仿真过程得到列车时刻表时，每一区间/车站直接加上对应的最小运行时间/停站时间，再加上强化学习模型所选取的动作作为缓冲时间，保证每个区间/车站满足最小间隔时间需求。对于列车发车时间约束，若按照Agent 直接选择的动作，列车会提前发车，将会直接在强化学习选择的动作上加上一定的时间，使列车在车站停站时间增加，以此保证列车不会提前发车。列车间隔和车站到发线数量两个约束将作为判断系统是否达到终止状态的条件之一。若任意约束条件不满足，系统将终止，重新开始下一轮仿真；否则，将继续列车运行仿真，直到所有列车到达车站K。因此，在仿真系统中，设置列车运行约束条件能保证所得到时刻表的可行性。

3.2 DRL动作

列车运行时间由区间运行时间和车站停站时间构成。本文将列车区间运行过程和停站过程均视为系统的时间步。列车在区间的运行时间由最小区间运行时间(由最大速度和区间里程确定)和区间冗余时间确定，车站停站时间由最小停站时间和车站冗余时间确定。因此，对于区间运行过程，DRL 模型的动作为该区间列车运行安排的区间冗余时间。对于车站停站过程，DRL 模型的动作为该车站需要的停站时间，l∈{1,2,…,L} ;k∈{1,2,…,2K-1,2K}。其中，表示列车l在位置k采取的动作。由于高速铁路系统可能存在不同速度等级列车(例如，速度等级为250 km·h-1的“D”字头列车和速度等级为350 km·h-1的“G”字头列车)，本文对不同速度等级列车设定不同的动作空间。

此外，为提高DRL模型选取动作的可行性，使用列车计划时刻表中的停站方案对列车停站时间动作进行动作掩码。因区间冗余时间无此要求，对区间冗余时间动作选取结果不进行任何操作。车站停站时间动作掩码为

3.3 列车运行状态

①列车到发时间状态转移

当列车处于出发状态时(将要进入区间)，需考虑列车在该站和下一车站是否停车。若停车，则需加上启停附加时间，其状态更新为

②列车晚点时间转移

各列车在各站到达和出发晚点时间由实际时间和计划时间确定。因此，模型中，列车晚点时间是实际时间和计划时间之差，即

③列车间隔时间转移

列车在k+1 位置(时刻)与前行列车的间隔时间同样可以通过2列列车的实际运行时间计算，即

式中：列车l-1是列车l在位置k+1的前行列车。

④列车是否停站转移

列车是否停站由计划时刻表给定。因此，对于该状态，任意时刻与之前时刻无直接关系，由列车计划时刻表给定，即

⑤列车到达/出发状态转移

列车到达和出发状态交替出现。因此，状态之间的转换概率为1，位置状态的概率为0，即

式中：“//”为求余数。

⑥列车位置转移

列车需从始发站运行到终到站，即从位置1到位置2K。DRL模型在选择动作时，只要选择的动作可以满足铁路系统的相关约束条件(例如，间隔约束和到发线数量约束等)，列车群将到达下一个位置。因此，位置状态参数更新方式为

式中：“|∃→∀”为所有列车运行相关的约束条件均满足要求；“ ”为条件。

3.4 DRL回报

仿真环境需给予智能体一定的奖励，使其探索更好的解。本文经过大量实验，最终确定选择的回报函数形式如下：当列车未到达位置2K时，系统每前进1步，将会得到1个较小的瞬时奖励，以此增加列车到达终点站的概率。此外，一旦列车群到达车站K(即最后位置2K)，系统将给予智能体较大的瞬时奖励M。此外，DRL 模型需尽可能使列车晚点时间更少，即各列车晚点时间需考虑到奖励中。由于DRL 系统目标是最大化奖励和回报，当达到最后位置2K时，从给予瞬时奖励M中减去所有列车在最后1个位置的总晚点时间。最后，系统回报R是各步瞬时奖励之和，即

式中：e为较小的常数；M为远远大于列车群在最后一个位置总晚点时间的整数。

4 案例分析

4.1 高速铁路线路参数

本文使用我国武汉到广州(武广)高速铁路广州北到长沙南区段作为模型测试环境。武广高速铁路广州北至长沙南区段全程约700 km，设计时速为350 km·h-1，分别经过广州北、清远、英德西、韶关、乐昌东、郴州西、耒阳西、衡阳东、衡山西、株洲西和长沙南，共11 个车站。该区段各站和区间参数如表1所示。此外，武广高速列车的启动附加时分为2 min，停车附加时分为3 min，即tac=2，tde=3。

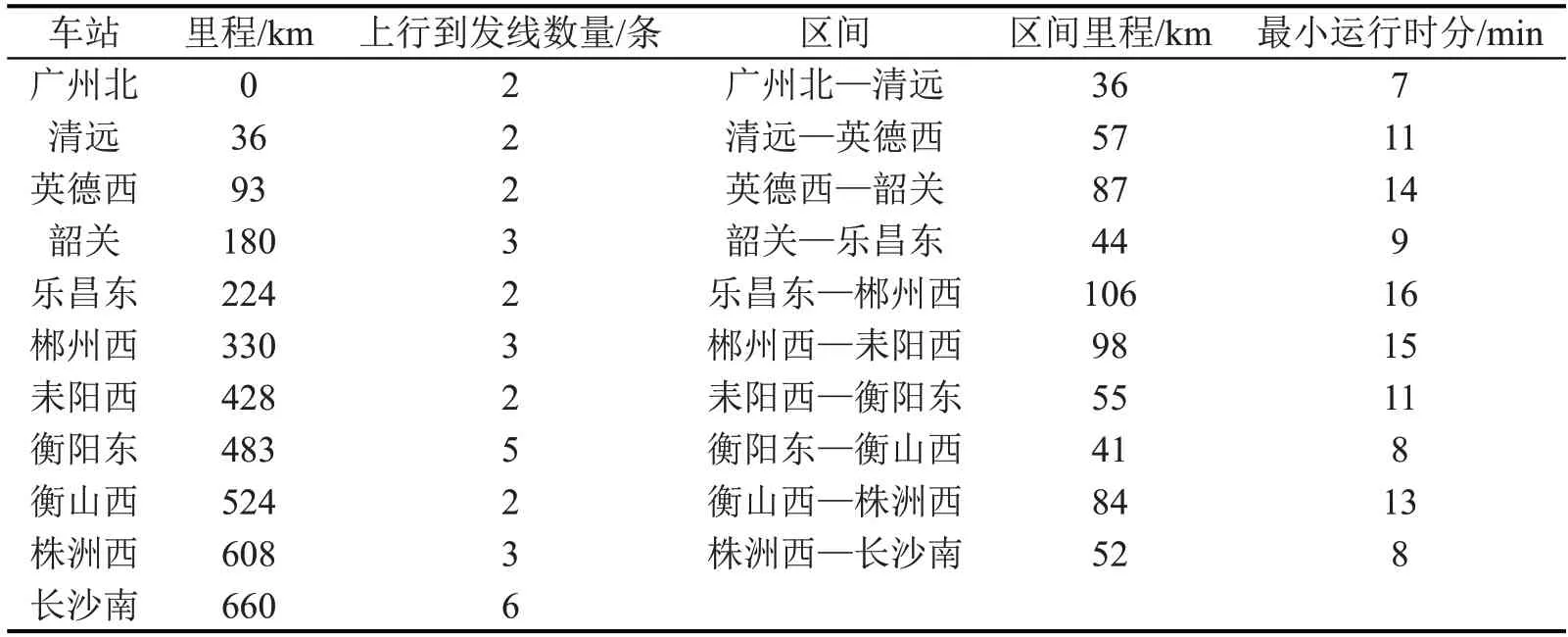
表1 武广高速铁路广州北至长沙南区段线路参数Table 1 Parameters of WH-GZ railway line

4.2 模型参数设置

在DRL 模型进行训练之前，需基于实验优化DRL算法参数。为确定模型参数，本文进行了多次实验。根据实验结果，选取的DRL模型参数如表2所示。此外，武广高速列车加速和减速时间标准、系统仿真时回报参数M和列车最小间隔时间标准等系统仿真参数设置如表3所示。

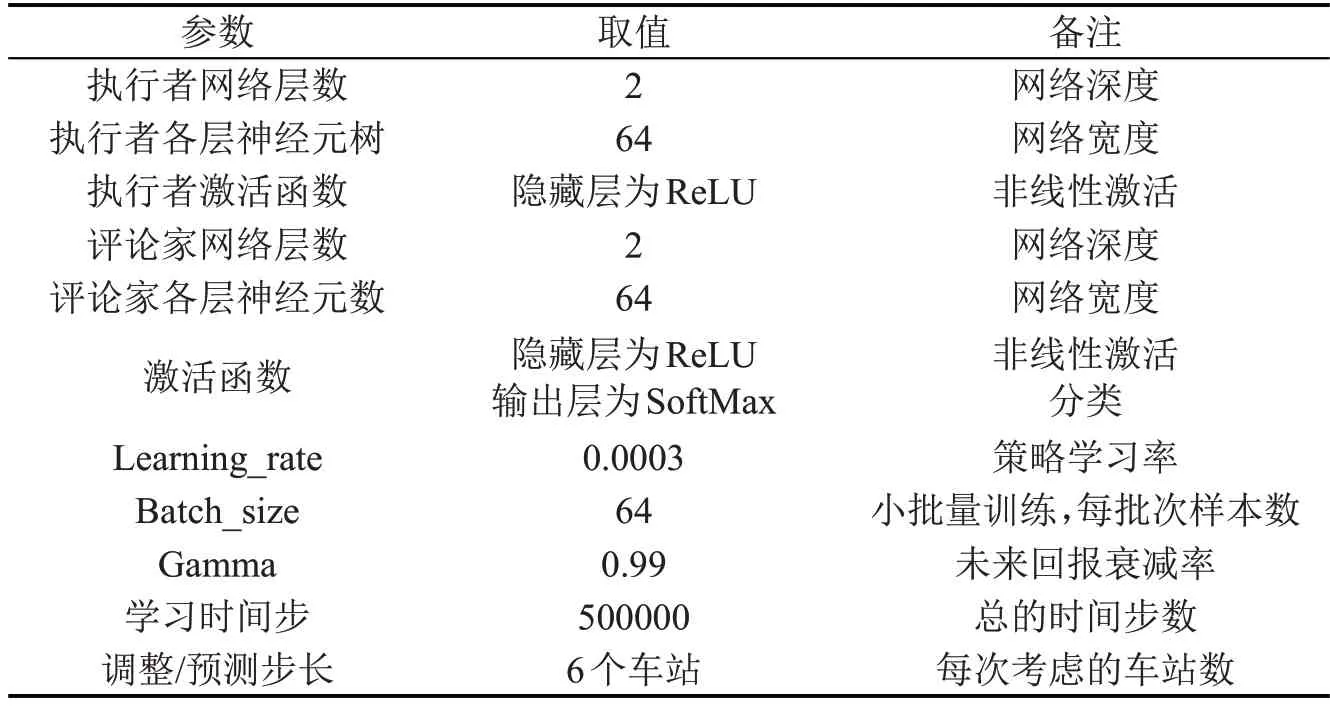
表2 DRL模型参数设置Table 2 Parameter setting for DRL model

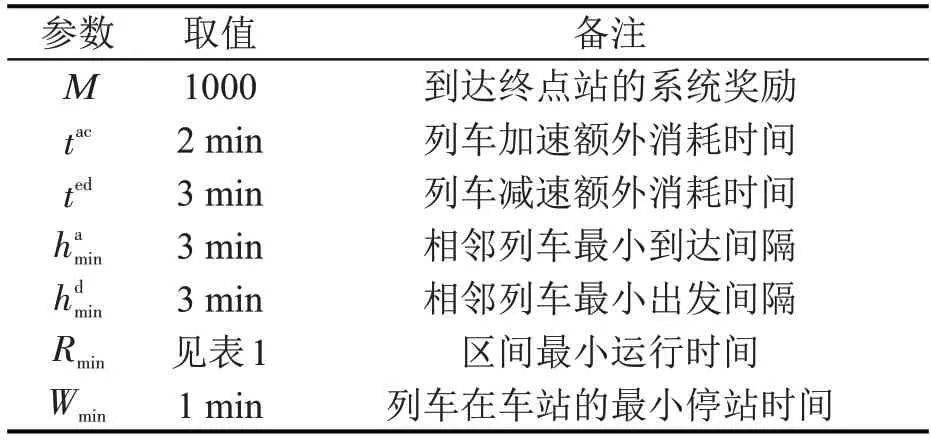
表3 仿真系统参数设置Table 3 Parameter setting for environment

4.3 实验设置

为展示模型效果，本文分别从随机干扰条件下和历史数据中选取两个不同案例验证模型。从随机干扰条件下选取案例可保证模型的实际可行性，从历史数据中选取案例可与调度员历史决策情况进行对比，各案例详细情况如下。

案例1 选取随机干扰条件下的时刻表调整。案例1 来自于武广高铁上行方向广州南至长沙南区段，干扰时间从10～90 min随机取值。此外，为更精确地模拟高铁现场调度指挥情况，受干扰列车后续可能受到二次干扰，二次干扰时间从10～30 min随机取值。由于随机干扰影响列车数参数未知，但建模时需考虑问题规模。因此，考虑干扰的可能时间长短，案例1 在每次仿真时，均考虑30 列列车。若对于选定的干扰时间值，部分列车未受干扰影响，则对这些列车不进行相应的时刻表调整。案例1中，通过计算机产生2次随机干扰，第1次发生在清远—英德西区间，干扰强度为38 min；列车通过第1 次干扰后，在乐昌东—郴州西区间受到第2次干扰，第2次干扰强度为15 min。

案例2 来自于广州北—长沙南区段上行方向，由线路设备故障导致。2015年11月21日，广州北上行方向进站咽喉处道岔发生故障，总计影响8 列列车，包括：1 列速度250 km·h-1的“D”字头动车和7列时速350 km·h-1的高铁列车。所有受影响列车中，最大晚点时间为45 min，最小晚点时间为8 min。

4.4 模型训练

本文建立的列车运行仿真环境考虑多个特征/状态，且各特征类型不同。为对比模型效果，同时测定两种能够处理多维状态特征的强化学习模型，即PPO 和A2C(Advantage Actor-Critic)。PPO 和A2C 是目前研究中应用最广泛和效果最好的强化学习模型。PPO和A2C模型在案例1和案例2上的训练结果如图5所示。

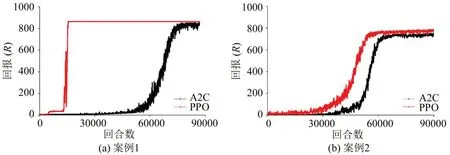
图5 PPO和A2C模型训练结果Fig.5 Training results of PPO and A2C

由图5 可知，对于案例1，PPO 模型能够在20000 步内快速收敛，A2C 模型需要约90000 步才能达到收敛。对于案例2，PPO 模型能够在60000步内收敛，A2C模型需要约70000步以后才能达到收敛。此外，对于两个案例，A2C 模型获得的回报均低于PPO 模型，表明A2C 获得的解的质量低于PPO模型，即PPO模型效果明显好于A2C模型。

4.5 模型结果评估

为验证PPO 模型的性能，选取A2C 模型、商业软件精确求解方法以及实际运行数据(调度员实际决策方案)作为对比。案例1 和案例2 的总晚点时间结果对比如表4 和表5 所示，基于PPO 模型的列车时刻表调整结果如图6所示。

表4 PPO和A2C模型在案例1上的性能Table 4 Performance of PPO and A2C on case 1 (min)

表5 PPO和A2C模型在案例2上的性能Table 5 Performance of PPO and A2C on case 2 (min)

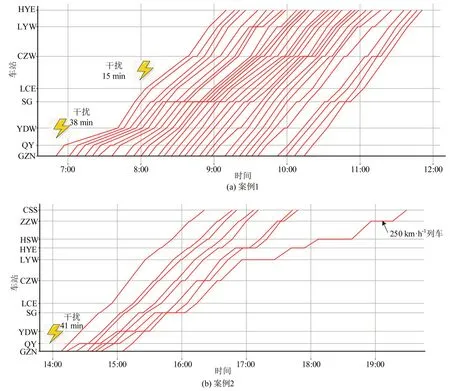
图6 基于PPO的干扰条件下列车时刻表调整结果Fig.6 Timetable rescheduling results based on PPO

在案例1 中，各方法对比结果显示，PPO、A2C及Gurobi求解结果中，列车到达衡阳东站总的晚点时间分别为254，291，249 min。由表4 可知，对于案例1，PPO 模型所得的解接近由Gurobi 得到的最优解(离最优解仅相差2.0%)，且明显优于A2C模型的解。PPO 模型相较于A2C 模型可减少约13%的列车总晚点时间。

对于案例2，PPO模型获得的解中，所有列车到达长沙南站的总晚点时间为188 min(其中，2 列列车实现完全恢复)。A2C 模型的总晚点时间为237 min，Gurobi求解结果的总晚点时间为184 min，而调度员决策方案的总晚点时间为258 min。由表5可知，PPO所得的解接近由Gurobi得到的最优解(离最优解仅相差2.2%)，且明显优于A2C得到的解。使用PPO 模型相较于A2C 和调度员决策方案，列车总晚点时间分别减少约20.7%和27.1%，由此表明，对于复杂案例2，PPO 模型优于A2C 模型和调度员决策方案。

由图6可知，案例1中，共包含30列车。其中，受两次干扰影响的列车共24列，未受影响的列车6列。案例1中，均为相同速度等级的列车，列车之间越行次数较少。案例2 同时包含不同速度等级列车，且各列车停站模式相差较大，图6(b)中，列车越行次数较多。此外，时速为250 km·h-1的“D”字头动车在乐昌东(LCE)站之前被时速为350 km·h-1的列车多次越行，以减小列车总晚点时间；当该列车经过耒阳西(LYW)车站时，晚点时间全部恢复，对后续列车无影响。因此，在图6(b)中，18:00 后仅展示了该列车。

4.6 模型时间消耗

为了解DRL 模型的效率，各模型的训练时长和执行时长如表6 所示。由表6 可知，PPO 模型在案例1和案例2上分别可在405 min和140 min内收敛。DRL模型最大的优势在于其可以离线训练，在线调用。因此，本文对保存的模型调用和执行测试时间也进行了记录，PPO和A2C模型在加载和执行测试时长均小于1 s，表明PPO 模型训练保存后可快速调用，可以满足实时调度指挥决策需求。

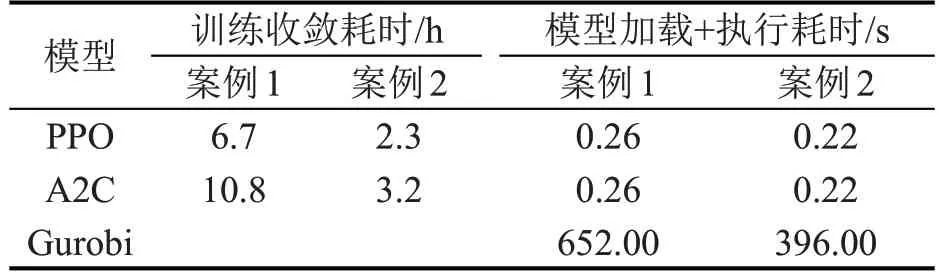
表6 模型收敛时长Table 6 Time cost of models

5 结论

本文针对干扰条件下高速铁路时刻表调整问题，考虑列车运行约束，以列车总晚点时间最小为目标，设计合理的智能体交互仿真环境，通过强化学习近端策略优化算法求解验证不同干扰强度情况下的武广高速铁路实例。结果证明，相比于其他强化学习模型，PPO模型在收敛速度和解的质量上具有明显优势，由PPO模型得到的调整方案的总晚点时间相较于A2C 模型和调度员决策方案可分别减少20.7%和27.1%。PPO模型得到的解与问题最优解仅相差约2%。此外，PPO 等强化学习模型可以离线训练，在线调用执行，调用和执行总耗时不超过1 s，相比于传统数学优化模型可以更好地满足现场实时决策需求。