考虑潜在冲突的进离场航班协同排序

王建忠，丁小芹，王树伟

(1.中国民航大学，空中交通管理学院，天津 300300；2.民航天津空中交通管理分局，天津 300300)

0 引言

虽然近年航空业受到了前所未有的冲击，但空中交通流量的增长势头依旧十分迅猛。美国联邦航空局(FAA)和航空工业预测未来20 年的增长率将在150%～250%之间[1]，预计到2025 年，全球航班的乘客将至少比2012 年增加50%[2]，到2037 年，全球机场处理的航空乘客数量预计将翻一番，达到约82亿人次。随着不断增长的交通量，空中交通拥堵愈发严重，终端区内航班出现大面积延误的概率大大提高，这不仅将对航空公司的运营成本产生不利影响，而且当频繁的延误在航空运输网络上蔓延时，将导致整个网络变得脆弱，使得乘客对航空运输的满意度日趋下降，同时给环境造成的不利影响也更加严重。

在确保航空器运行安全的前提下，为提高终端区运行效率以及跑道资源利用率，缓解航空运输网络上的延误问题，国内外专家针对进离场航空器的排序问题展开一系列研究。王菲等[3]实现对离场航空器的实时动态排序，确定允许开车时间为管制员提供决策支持；Faye 等[4]使用间隔时间矩阵和时间离散化来研究单跑道和多跑道飞机着陆问题；Murça等[5]开发了用于飞机着陆排序和调度的混合整数线性规划模型，通过特定航站楼到达路线控制机场交通流的问题，并结合着陆时间窗和优先权的操作约束，实现动态环境下的优化；Díaz等[6]依据噪声对人群的影响将噪音指标与飞机排序结合起来，并使用西班牙马德里机场的真实数据，比较取不同的最大位移约束值对模型产生的影响；张启钱等[7]以管制负荷与航班延误总成本最小为目标，采用滚动时域控制策略建立进离场航班多目标动态优化模型；王宁等[8]考虑点融合程序下终端区航空器排序问题，提出以0-1 整数规划为基础的多跑道进场航班优化排序模型；Oren等[9]提出多到达路线点融合系统，基于每架飞机的航路分配和航路点分配实现最优排序；马园园等[10]从时空维度引入“航班满意度”的概念，探索多机场交通流排序方法；张军峰等[11]引入“外围航班流”的概念，以最小化航班延误为目标，建立多机场进离场协同排序模型。

目前国内外对于航空器进离场排序优化的研究成果颇多，但现有研究仍存在以下不足：(1)在进离场排序优化过程中，对于管制员负荷的问题，通常仅从航空器位置转换次数或发生延误的航空器数量等方面作简单处理。(2)常使用的各种优化策略均为航空器着陆、起飞提供一个具体的时间点，但在实际运行过程中时常会出现干扰或误差，此时模型的优化结果将很可能不再具有可操作性。针对上述问题，本文以进离场航班为对象，通过具体分析进离场航班间潜在冲突，考虑管制员在实际指挥过程中需要花费时间精力发布指令(加速、减速、改变飞行角度等)对飞机间存在的潜在冲突问题进行解脱，从时间维度利用潜在冲突发生时长刻画管制员解决冲突的负荷，建立多目标时间索引模型，在为每架航空器分配着陆、起飞时隙，提高模型优化结果抗干扰能力的同时尽可能减少进离场航班潜在冲突，以最大程度降低由排序引起的管制员负荷增加，达到提高终端区运行效率和安全的目标。

1 进场和离场航班潜在冲突分析

1.1 进场-离场冲突分析

设t=0 时第一架航班到达下降顶点或抬轮离地，此时进场航班g所在高度为h，下降率为b，水平速度为vg，到航线交叉点o的距离为dg；离场航班f的上升率为a，水平速度为vf，到航线交叉点o的距离为df；航班最小垂直间隔为sfg，最小水平间隔为；航线间夹角为α、β、λ、γ，具体如图1所示。t时刻航班的所在位置详见下文。

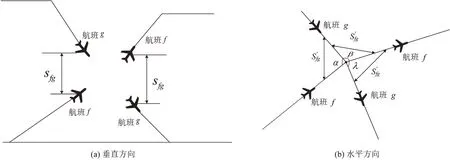
图1 进离场航班潜在冲突示意图Fig.1 Schematic diagram of potential conflicts on arrival and departure aircraft

1.1.1 垂直方向分析

离场航班f所在高度hf=at，进场航班g所在高度hg=h-bt，则两航班之间的高度差为Δh=|h-(a+b)t|。

情形1 Δh∈[sfg,+∞)，航班f和航班g在垂直方向上无冲突。

情形2 Δh∈[ 0,sfg)，航班f和航班g垂直间隔不满足，垂直方向上存在冲突，且在管制员无干预的情形下，航班f和航班g之间的垂直间隔先减小后增大。令Δh=sfg可得，则垂直方向上的冲突时间为[t1,t2] 。

1.1.2 水平方向分析

情形1 离场航班f为前序航班，在tf=时刻到达航线交叉点o，设此时进场航班g到航线交叉点o的距离为L，则到达航路交叉点o的时间tg=tf+Lvg。

(1)当t∈(-∞,tf)时，两架航班之间的距离平方为

(2) 当t∈[tf,tg] 时，两架航班之间的距离平方为

(3)当t∈(tg,+∞)时，两架航班之间的距离平方为

同理可得情形2，当进场航班g为前序航班，航班g到达航路交叉点o的时间tg=dgvg，进场航班f距离航线交叉点o为L，到达航路交叉点o的时间tf=tg+Lvf时，可得到如下冲突临界时刻：

综上所述，通过计算可得航班f和航班g之间所有可能发生水平冲突的临界时刻，再结合具体航班速度、航线夹角分布等情况，便可获得水平方向上冲突持续时间区间。当离场航班f为前序航班时，[t3,t4]=[min{ta,tf,tb,tc,tg},max{ta,tf,tb,tc,tg} ]；当进场航班g为前序航班时，[t3,t4]=

若[t1,t2] ∩[t3,t4]=∅，则说明航班f和航班g之间至少满足一个方向上的最小间隔要求，两航班之间无冲突发生；若[t1,t2] ∩[t3,t4]=[ts,tx]，则说明航班f和航班g在区间[ts,tx]上水平和垂直最小间隔要求均不满足，两航空器之间存在冲突，需要管制员干预，且当[ts,tx] 区间长度越大时，需要管制员付出的精力就越多，所产生的工作负荷就越大。

1.2 进场-进场冲突分析

对于两架离场航班而言，由于本文以单跑道为研究对象，故不特别考虑离场航班间的交叉航线潜在冲突问题，仅在模型的间隔约束部分考虑使用同一离场航线的时间间隔。

2 问题描述与建模

2.1 问题描述

为减少进离场排序中由潜在冲突引起的管制员工作负荷增加，提高排序结果的可执行性，本文以单跑道运行为背景，设航班集合为F=F1∩F2，其中，F1为进场航班集合，F2为离场航班集合，引入Heidt[12]提出的时间索引模型，以步长Δt将优化时间区间TD=[tstart,tend] 离散化为时间点集TD={tstart,tstart+Δt,tstart+2Δt,…,tend} 。用区间表示航班i的最早和最晚着陆或起飞时间，通过两者取交集的方式，可将航班i的有效着陆或起飞时间点表示为

最终可将航班i的起飞或着陆时间安排在相邻有效时间点和之间的时隙上。

基于以上，本文致力于建立多目标时间索引模型，为进离场航班分配起飞和着陆时隙。

2.2 多目标时间索引模型

2.2.1 优化目标

航班延误时间和管制员工作负荷是影响终端区运行效率和安全的重要影响因素。因此，以进离场航班的总体延误时间最小以及排序中潜在冲突引起的管制员工作负荷增加最小为优化目标，建立进离场航班协同排序的多目标时间索引模型，即

2.2.2 约束条件

(1)时隙约束

式中：ωi,m、ωj,m为0-1变量，当航班i或航班j在时隙m上时等于1，否则为0。式(11)表示一个时隙最多只能安排一架进离场航班；式(12)和式(13)表示一架进离场航班只能分配给一个时隙。

(2)安全间隔约束

当一架航班被分配在时隙m上时，为了保证最小安全间隔，则相邻的另一架航班将被禁止安排在以下时隙上

由于不同运行状态的航班之间应该满足不同的最小安全间隔，因此本文设定最小安全间隔集合δ={δA,δD,δAD,δDA}，整合不同运行状态下相邻两架航班之间的安全间隔约束。其中，δA为两架进场航班的最小时间间隔；δD为两架离场航班的最小时间间隔，对于使用同一离场航线的连续航班，则需要在原有的最小时间间隔上增加时间ΔtD以避免发生冲突；δAD为先进场后离场航班的最小时间间隔；δDA为先离场后进场航班的最小时间间隔。

(3)位置转换约束

在基于先到先服务的航班序列基础上，每架航班的移动位置不能超过其最大偏移量，即

式中：Ni为先到先服务模式下航班i在队列中的序号；为经过优化后航班i在队列中的序号；M为最大位置偏移量。

3 求解算法

进离场航班协同排序问题是典型的NP-hard问题[10]。确定航班最佳起飞着陆顺序的计算量是一个阶乘函数，具有高度复杂性，因此近年来的研究大多集中在开发启发式求解算法上[13]。从以往的研究结论中可知，在航班排序调度等优化模型的求解计算方面，相比于CPLEX等商业求解器，启发式算法的运算能力更强，对于同样的优化模型，启发式算法可能在几秒至几十秒内找到最优解，而CPLEX等商业求解器则可能需要几十分钟甚至更长，很难满足空管系统内实时排序的需求。为此，设计遗传算法对模型进行求解。

优化模型涉及进离场航班总延误时间以及排序中潜在冲突引起的管制员工作负荷增加，为便于后续计算，利用加权求和的方法将多目标问题转化为单目标问题。

3.1 编码方法

针对进离场航班协同排序问题特点，采用序数编码策略，生成可以直接表示进离场航班顺序的染色体序列，再通过结合位置转换约束条件生成部分初始可行解。序数编码方式不仅可以直观表示航班集合，便于后续时隙分配和约束条件的验证，而且加快初始解生成速度提高计算效率。

3.2 适应度函数

模型涉及的多目标函数均为最小型函数，故将适应度函数F定义为两个带有一定权重w1、w2的目标函数Z1、Z2之和的倒数，即

针对给定的航班起降次序，首先按照顺序依次为航班分配既能减少延误时间又可以满足最小安全时间间隔的时隙，确保所有进离场航班既满足时隙约束又满足安全间隔约束；然后按照分配的时隙计算给定次序对应的适应度值。

3.3 遗传操作

选择操作利用代沟来控制每代中种群被替换的比例，再结合随机遍历抽样方法获得继续进行交叉、变异的种群。随机遍历抽样方法在轮盘赌方法的基础上得到进一步优化，它等间距的选择不同适应度的个体，使得每个个体被选中的机会“均等”，有利于保持种群的多样性。

对选择得到的种群采用部分匹配交叉的方法。随机在父代染色体上选择一个基因位作为交叉起点，并选择自起点位向后的第5个基因位为交叉终点，将这两点间的基因进行交换，交换完成后进行冲突检测以确保子代染色体中没有重复基因，部分匹配交叉流程如图2所示。

图2 部分匹配交叉示意图Fig.2 Diagram of partially-matched crossover

变异操作则是随机选取某一基因为变异对象，交换该基因与下一位置基因的次序。

通过不断的交叉、变异操作增加种群多样性，使得种群能够在搜索空间中被更广泛的探索。最终以达到设置的最大迭代次数作为终止条件，求得使总延误时间和管制员工作负荷加权之和最小的序列集合，再从集合中选取与实际运行情况下差异最小的序列作为最佳进离场序列。

4 实例验证与结果分析

选取天津滨海国际机场2018年12月1日16跑道13:00-14:00 的数据作为实验样本，如表1 所示，包括14 架进场航班和14 架离场航班；机场航线冲突点和基础数据如图3所示，东侧主要以进场航班与离场航班冲突为主，西侧主要以进场航班与进场航班冲突为主，对于两架使用同一离场航线的航班，这里将两者之间的最小安全间隔时间扩展到5 min；航班的机型大多为中型机，仅包含少量重型机，无轻型机，因此本部分仅考虑重型机与中型机之间的最小间隔标准，将距离标准转化为时间标准，结果如表2所示。

表1 进离场航班样本数据Table 1 Arrival and departure aircraft sample data

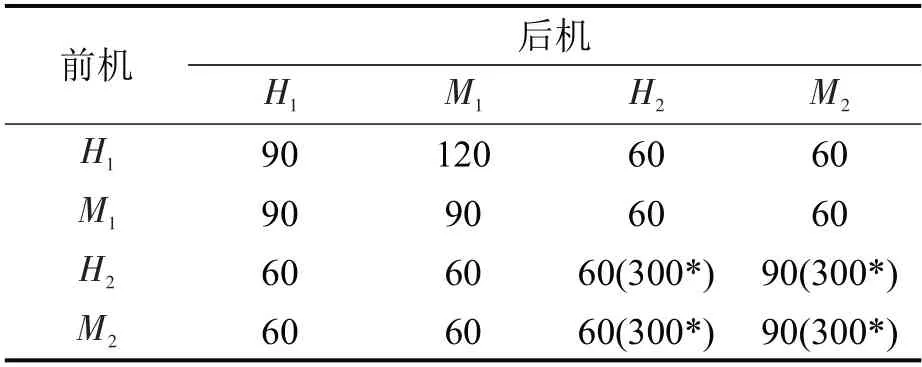
表2 航班最小时间间隔标准Table 2 Minimum time separation standard for aircraft (s)

除表1中可直接获得的数据外，本文还需要计算得到进离场航班的最早着陆、起飞时间，最晚着陆、起飞时间。结合进离场航班的航线信息，各机型速度信息(表3)等，计算得到表4所示的结果。

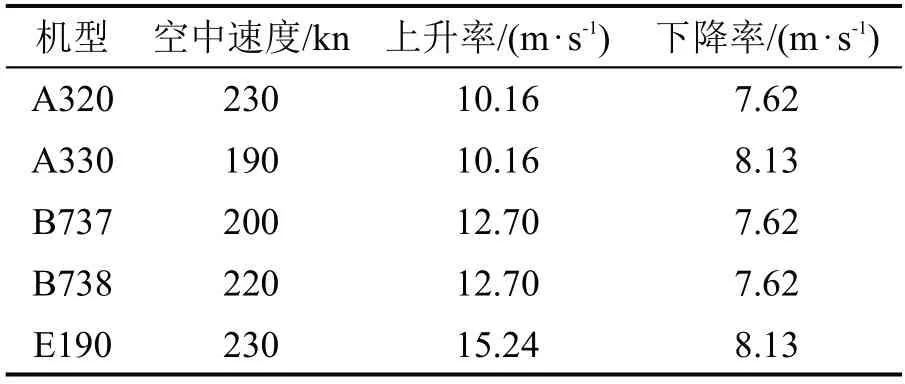
表3 各机型速度参数设置Table 3 Speed parameter settings for each aircraft

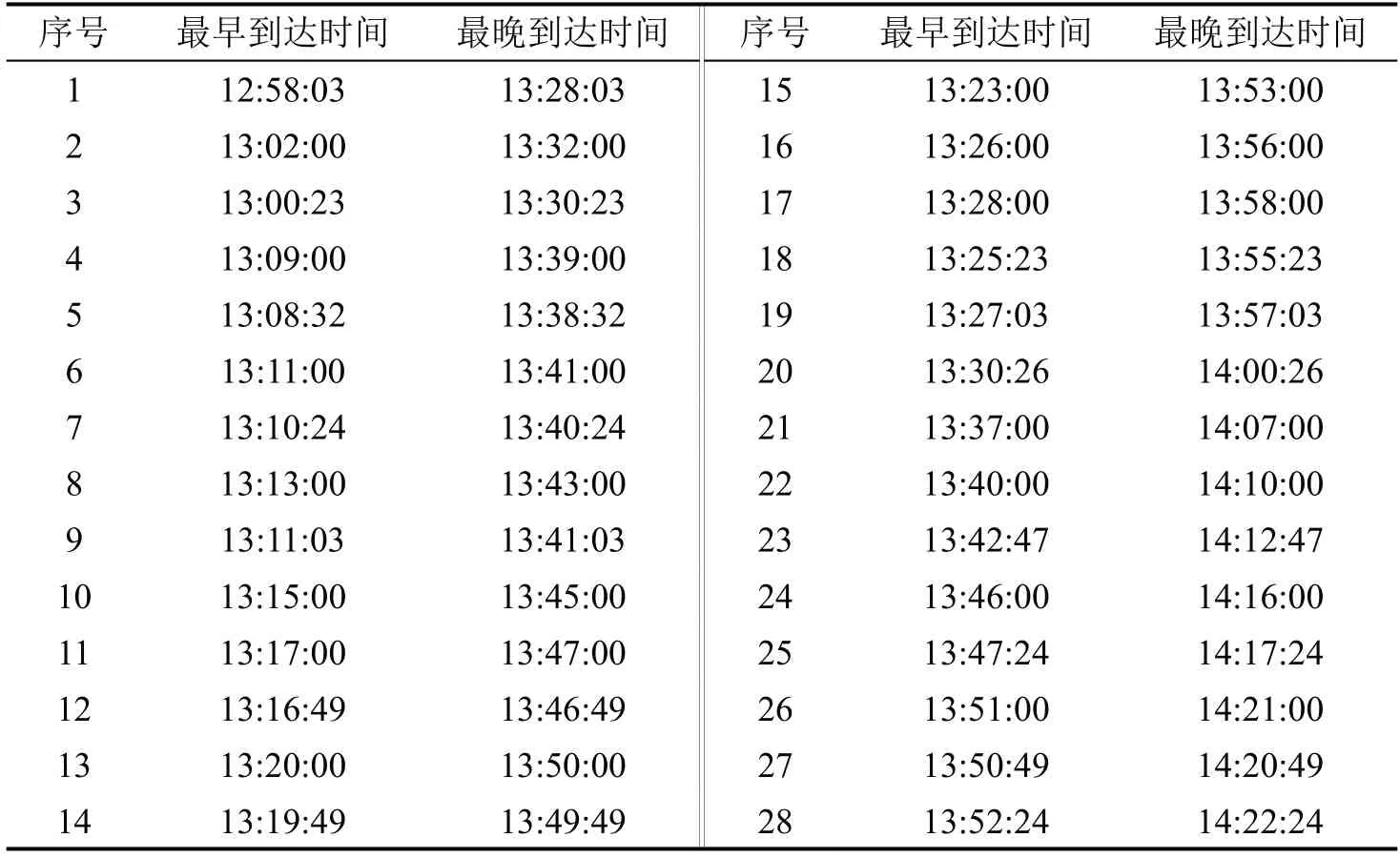
表4 相关数据计算结果Table 4 Relevant data calculation results

基于以上数据，采用遗传算法进行求解，种群规模设置为20，交叉率0.9，变异率0.1，代沟0.9，最大迭代次数200，最大位置偏移量3，Δt=5 s，对上述28架进离场航班进行计算。在先到先服务策略和实际运行情况下，计算结果如表5所示。

表5 先到先服务结果和实际运行结果Table 5 First-come-first-served results and actual operation results (s)

通过设置不同数据组合寻找对优化延误时间和管制负荷均有利的权重组合，结果如表6所示。

表6 不同权重的计算结果Table 6 Calculation results of different weights

由表6可知，当不断提高目标函数2的权重时，虽然航班延误的优化比例有所降低，但管制负荷优化的比例却快速提高。

为进一步观察两目标函数间的关系，绘制目标函数解的Pareto 最优前沿，如图4 所示。从图中可得，延误时间最小化与管制员工作负荷最小化之间存在一定的矛盾关系，在优化求解时无法找到两者同时达到最优的排序结果，为此需要通过设置权重来选择符合期望的排序结果。

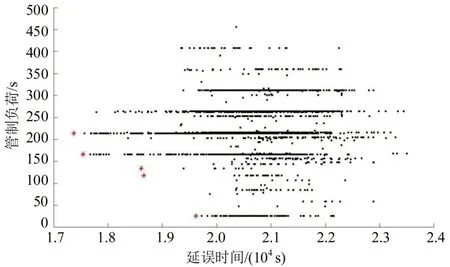
图4 帕累托最优前沿Fig.4 Pareto optimal front

在繁忙的终端区内，对于降低航班延误时间和减少管制员负荷两者同样重要，希望获得既可以有效减少航班延误时间，同时又可以减轻管制员工作负荷的排序结果。选择0.2-0.8 的权重组合作为目标函数的权重值，结果如表7所示。

5 结论

本文的主要结论如下：

(1)所建立的进离场航班协同排序多目标时间索引模型，为进离场航班分配起飞和着陆时隙，将每架航班的起飞、着陆可执行时间扩展到一段时间内，而非一个时间点上，在提高终端区运行效率和安全的同时，可获得鲁棒性更高的航班序列。

(2)通过分析序列中航班的潜在冲突情况，利用潜在冲突时间长度表征管制员工作负荷增加，在模型优化求解后，由排序中潜在冲突引起的管制员负荷增加可得到有效减少。

(3)通过为目标函数设置不同的权重组合，可得当目标函数2 的权重在0.7 以下时，管制员工作负荷的优化率较低；当权重大于等于0.8时，管制员工作负荷得到明显减少，优化程度大大提高。