基于列车开行方案的城市轨道交通多交路客流分配方法

许得杰，潘星，巩亮，胡晨皓，王雪鑫

(1.兰州交通大学，交通运输学院，兰州 730070；2.中铁第一勘察设计院集团有限公司，西安 710064)

0 引言

随着我国城市轨道交通网络化运营的不断深入，长大线路和复杂线型的多交路共线运营、多网融合的贯通运营和互联互通跨线运营已成为我国轨道交通发展的重要方向。因此，研究多交路共线运营客流分配理论，对城市轨道交通复杂交路设计、开行方案优化调整和票务清分等具有重要意义。

目前，针对常规公交系统共线运行的客流分配方法经历了从解决共线问题到网络均衡配流两个阶段。乘客对共线运行线路的路径选择行为称为共线问题，最早由CHRIQUI 等[1]提出，并将共线问题抽象为以乘客期望旅行时间最短为目标的优化问题。随后，NGUYEN等[2]将共线问题转化为公交网络的最短超路径问题，提出基于图论的公交网络变分不等式客流分配模型。COMINETTI 等[3]考虑拥挤效应对乘客路径选择行为的影响，构建拥挤条件下的共线问题及其客流分配模型。在共线运行网络配流方面，SPIESS等[4]定义了乘客路径选择问题的优化策略概念，并假定乘客选择乘坐优化出行策略中的第1趟到站列车，构建非拥挤条件下公交网络的客流分配线性规划模型。CEPEDA等[5]考虑拥挤效应和能力约束，构建拥挤条件下基于发车频率的客流分配模型。CODINA等[6]考虑拥挤条件下具有严格能力约束的网络配流问题，构建基于变分不等式和不动点理论的均衡客流分配模型，研究不同拥挤程度下交通分配模型的有效性和可靠性。上述研究将公交服务频率和运行时间定义为关于流量的函数，而轨道交通服务频率和运行时间一般不随流量变化，故上述方法不能直接用于轨道交通。

近年来，随着轨道交通互联互通和多网融合的发展，针对网络化运营条件下的客流分配越来越受到关注。SCHMOCKER 等[7]将乘客路径选择中是否有座位的因素引入乘客路径选择模型中，设计共线运行网络上的马尔可夫式客流加载机制，构建基于发车频率的轨道交通客流分配模型。倪少权等[8]构建无隐性连接的3层多制式轨道交通拓扑网络，并考虑乘客路径选择影响因素对广义出行费用的影响，建立基于Logit 模型的多制式轨道交通客流分配模型。许得杰等[9]针对多交路共线运营线路，提出基于发车频率和乘客出行区段划分的客流分配方法。为增强客流分配方法适用性，进一步提出基于超路径出行策略的轨道交通多交路客流分配方法。REN 等[10]通过定义乘客出行选择行为中的线路策略和节点策略，构建变分不等式用户均衡客流分配模型。茧敏等[11]根据AFC 数据和列车时刻表数据，提出基于乘客出行时空路径推算的网络客流分配方法。当城市轨道交通多交路运行时，乘客会面临不同交路列车的选择问题。对具有高服务频率(发车间隔小于10 min)的城市轨道交通系统，乘客路径选择是建立在共线问题的出行策略(备选路径集合)上的，即乘客在出行前不能确定选择哪条路径，而是在出行前确定一个出行策略，并在出行过程中根据列车的到站情况选择策略中的一条路径，而上述研究忽略了轨道交通共线运行时乘客路径选择行为的特殊性，在配流模型中也并未考虑这一问题。基于开行方案和列车时刻表的客流分配方面，李文卿等[12]基于高铁旅客出行选择行为，通过设计基于开行方案搜索的两阶段寻路算法，提出基于列车开行方案的客流分配方法。史峰等[13]构建基于列车时刻表的高铁出行时空网络，将离散客流高铁均衡分配问题等价于具有列车席位能力约束的多个OD离散需求的最小费用流问题，并建立基于列车时刻表的客流分配模型。上述研究均认为高速铁路不允许超员或少量超员，不需考虑车厢内的拥挤度，即路径广义费用不受乘客拥挤感知的影响，但城市轨道交通列车高峰期拥挤现象明显，路径广义费用与乘客拥挤感知紧密相关，因此，上述方法与城市轨道交通客流分配方法存在差异。

综上，本文运用网络客流分配理论，研究轨道交通共线运行乘客路径选择行为，并提出共线运营客流分配模型和求解算法，旨在解决基于复杂多交路共线运营开行方案的客流分配问题。

1 多交路共线运营服务网络构建及共线问题

1.1 多交路共线运营服务网络构建

典型多交路共线运营线路及列车开行方案如图1所示。该线路包括6个车站，分别为S1～S6；列车停站方案采用站站停模式，交路计划包含3条交路，各交路列车发车频率fi=10 对·h-1，i=1,2,3，fi表示交路i的发车频率，交路1 列车编组n1=6 辆；交路2 和交路3 列车编组n2=n3=3 辆。在多交路运营时，不可避免地会出现列车共线运营的情形，例如，区段S1～S3由交路1 和交路2 列车共线运行。由于共线区段的乘客会选择乘坐不同交路的列车，相当于乘客的路径选择行为。为刻画乘客路径选择行为，关键是将多交路共线运营列车开行方案转化为共线运营服务网络。

图1 典型多交路共线运营线路及列车开行方案Fig.1 Typical railway of common-line operation with multi-routing and train plan

假定多交路共线运营服务网络表示为G=(N,E)，N和E分别表示节点集合和弧段集合。其中，N包括车站节点集合Ns和交路节点集合Nr，即N=Ns∪Nr；E包括候车弧、下车弧和乘车弧，弧的权重分别表示候车、下车和乘车阻抗。以图1中的车站S2为例，应用共线运营服务网络节点表示方法(仅上行方向)，如图2所示，可以将车站转化为服务网络中的节点。按照该方法，可将共线运营多交路的所有车站转化为服务网络节点，即可得到多交路共线运营服务网络。为方便后续算法中的递归调用，节点标号采用头节点小于尾节点的方式。该服务网络中，任意车站节点可视为不同交路列车间的换乘节点。

1.2 轨道交通共线问题及其数学描述

城市轨道交通多交路共线运营时，乘客在共线区段的路径(交路)选择是客流分配的重点，即相邻两节点间路径选择的共线问题。考虑仅有1个OD对(o,d)和m条线路的简单网络，如图3(a)所示。令E为线路ei的集合，即E={ei|i=1,2,…,m}，ei为从o至d的第i条线路。假定乘客以期望总出行时间最少为目标选择路径，则乘客期望总出行时间为

图3 共线问题及出行策略Fig.3 Common-line problem and trip strategy

图4 超路径及弧段客流分配概率Fig.4 Hyperpath and passengers'assignment probabilities of arcs

2 基于发车频率的超路径客流分配方法

对于多交路共线运营服务网络，乘客的路径选择行为不仅包含相邻两节点间的共线路径选择问题，还包括非相邻两节点间的路径选择问题，即文献[2]中的超路径问题。在路径选择过程中，出行策略(即有效路径)的确定是关键。在多交路共线运营服务网络中，出行策略的确定可以转化为求解服务网络中的最短超路径问题。最短超路径是乘客期望出行时间最短的路径集合(即出行策略)，相关理论见文献[9]，此处不再赘述。以下给出在获得最短超路径之后，将客流分配在超路径弧段上的方法。

3 多交路共线运营服务网络客流分配模型构建

在多交路共线运营服务网络基础上，考虑站间OD 需求和流量守恒约束，构建共线运营服务网络客流分配模型。

3.1 服务网络中节点流量守恒约束

服务网络G中有多个OD对需求，且需求仅在车站节点之间存在。令目的节点集合D⊆Ns，对任意车站节点i,d∈D且i≠d，有需求≥0 。令V=[0,∞)E×D表示弧段流量向量v的空间，弧段e上流向目的节点d的流量≥0。对任意弧e∈，有=0，则满足以下节点流量守恒约束条件，即

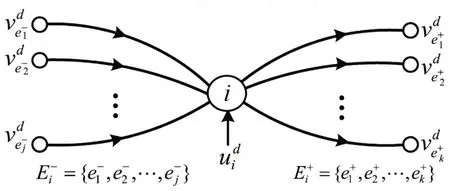
图5 流量守恒约束条件Fig.5 Constraints of flow conservation

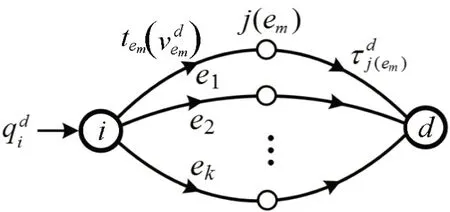
图6 局部网络共线问题Fig.6 Common-line problem of local network

3.2 网络平衡模型构建

Wardrop平衡条件为

式(11)表示节点i的流入量与流出量相等；式(12)表示共线线路上的流量为各出行策略分配到该线路的流量之和；式(13)中表示从i到d的最小期望旅行时间，该时间可以在求解最短超路径时同时得到。出行策略s的旅行时间为

式中：左侧第1项为i至d各线路总在车旅行时间；第2项为总候车时间；右侧为总期望旅行时间。当网络达到平衡状态时，等式成立。因此，可将求解平衡解转化为求解差值函数的最小值，即

4 求解算法

轨道交通共线客流分配模型包括：共线问题、最短超路径问题及客流分配模型，具体算法如下。

4.1 共线问题求解算法

针对轨道交通共线问题，其决策变量为xl，该问题本质上为(0,1)双曲规划问题(Hyperbolic Programming Problem)的特殊形式(a0=α,b0=0)。该问题可以采用枚举法、遗传算法和贪婪算法求解。由于贪婪算法思路简单，易于实现，因此，被广泛应用，该算法的核心思想是：将m条共线线路按乘车时间长短依次排序(t1＜t2＜…＜tm)，并令初始解X*==(1,0,…,0)，其中，xei=1，表示第i条线路ei被乘客选择，=0，表示该线路未被选择。令期望出行时间Ts(X*)=(X*)+t1；然后，依次加入共线线路2，即令X=(1,1,…,0)，若Ts(X)＞Ts(X*)，则停止；否则，令X*=X，重复计算，直至停止，Ts(X*)即为最优解，X*即为乘客出行策略。

4.2 客流分配模型求解算法

客流分配模型的核心是加载流量最短超路径的获取，故在模型求解中将最短超路径算法嵌入连续平均算法(Method of Successive Average,MSA)中，形成混合MSA算法。对多OD对轨道交通服务网络G，客流在网络上的加载需要求解任意OD对之间的最短超路径。由于最短超路径算法需要任意OD 对之间的子服务网络G′，首先，需要从网络G中提取子网络G′，然后，再将子网络输入SFT(Shortest Forward Tree)算法中得到最短超路径。在求解过程中，需要判断超路径中基本路径的有效性。本文设定有效性判断规则为：①乘客一次出行换乘次数至多为2 次；②一次出行中不能重复乘坐同一交路列车，即乘客如果由本交路列车换乘到其他交路列车，则不能再换入本交路列车；③路径无圈。SFT 算法在文献[9]中给出，此处不再赘述。MSA算法具体步骤如下：

Step 1 初始化

Step 2 迭代计算差值函数G(vk)的值

Step 2.2 应用SFT 算法计算OD 对最短超路径，并根据超路径弧段客流计算方法计算附加流量。

Step 2.4 令k=k+1，根据式(17)计算G(vk)。

Step 3 收敛性判断

若G(vk)＞ε，则返回Step 2；如果G(vk)≤ε，则输出平衡状态流量vk，结束。

5 算例研究

5.1 算例验证及分析

由图7可知，车站9—车站1的乘客选择了两条路径。其中，路径1 为直达路径：9→8→2→1，流量为100.7；路径2 为换乘路径：9→7→6→5→4→3→1，流量仅为19.3。由于换乘存在二次候车，因此，换乘路径的阻抗一般要大于直达路径的阻抗。对于共线运营区段的跨交路乘客，会优先选择直达路径，当直达路径的阻抗大于换乘路径的阻抗时，换乘路径也会被选择，这种针对跨交路出行乘客对直达路径的选择偏好在求解最短超路径中可以体现。两条路径的流量分别为100.7 和19.3，在车旅行时间分别为49.6 min和55.6 min(车站5的换乘时间为6 min)，候车时间为6 min，期望出行时间=55.6 min，根据式(17)可得，G(v)=0，满足平衡解算法精度，验证了本文模型和算法的有效性。

图7 服务网络算例及配流结果Fig.7 Service network and its assignment results

为对比分析多编组与多交路和固定编组与多交路两种开行方案下的客流适应性和分布情况，以图1 所示多交路运营线路为基础，设计两种开行方案。为便于对比分析，两种方案的列车交路形式和发车频率均保持相同，仅编组方案有所差异。方案1为多编组方案，3 条交路的列车编组为(6,3,3)；作为对比方案，考虑车辆总数保持不变，设计方案2 为固定编组方案，列车编组为(4,4,4)，具体如表1 所示。多交路共线服务网络如图8 所示，有6个车站，3条交路，包含20个节点，33条弧段。车辆座位数和定员分别为c1=31 个·辆-1，c2=310 人·辆-1；拥挤感知参数和相对误差ε取值同上。各弧段时间为：乘车弧时间如图8 所示，共线运营乘车弧时间相等，例如，==8 min ；候车弧时间=0.5 min，ei∈,j∈Ns；下车弧时间=0,ei∈,j∈Ns。车站客流需求为OD(i,d)=4500人次，i≠d且∀i,d∈Ns。算例求解采用Matlab 2014(b)编程，CPU 为i5-4440，内存为4 G 的电脑执行，求解耗时为25.2 s，客流分配结果分析如表1所示。

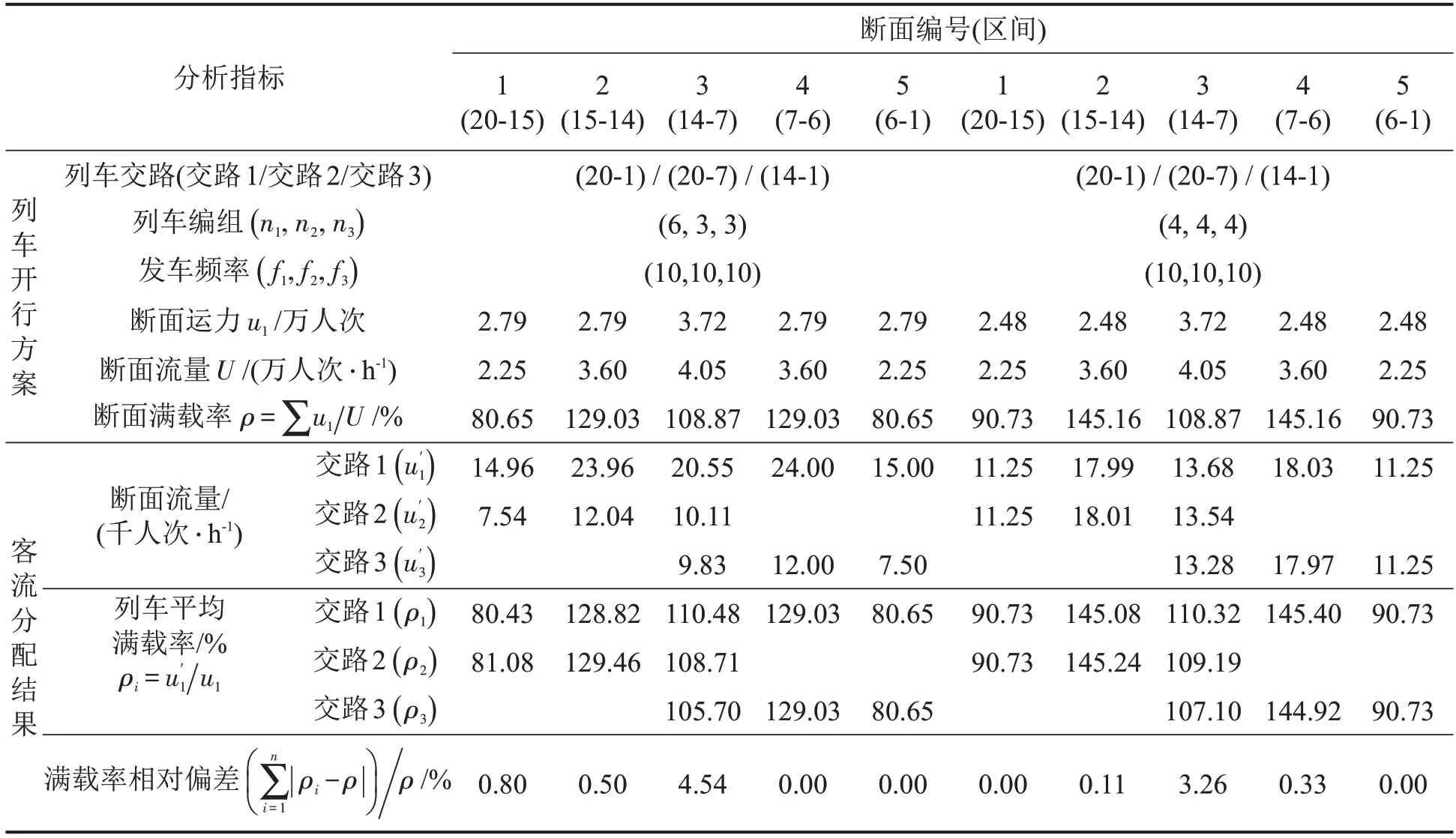
表1 客流分配结果分析Table 1 Analysis of passenger assignment result

对比多编组和单一编组两种运营模式，可以发现，编组为(6,3,3)时，列车平均断面满载率最大值为断面2的129.46%，而编组为(4,4,4)时，同一断面的满载率高达145.24%，与实际不符；在断面1、断面4 和断面5，多编组下的列车平均满载率均低于单一编组下的值，在断面3，两种编组模式下的满载率基本相等，可见多编组模式的客流适应性较单一编组模式强。因此，在相同的服务频率下，合理安排列车编组可以更好地适应客流需求，使运力与需求更加匹配，服务水平更高。

5.2 不同客流分配方法对比分析

为研究不同客流分配方法的优劣，选取文献[9]中基于超路径的客流增量分配方法(方法1)和本文配流方法(方法2)，以图7所示多交路共线运营服务网络为例进行对比分析，其中，列车开行方案(表1)和基础参数均与图7 算例相同，方法1 和方法2 的模型参数与文献[9]相同。两种客流分配方法的配流结果如表2所示。

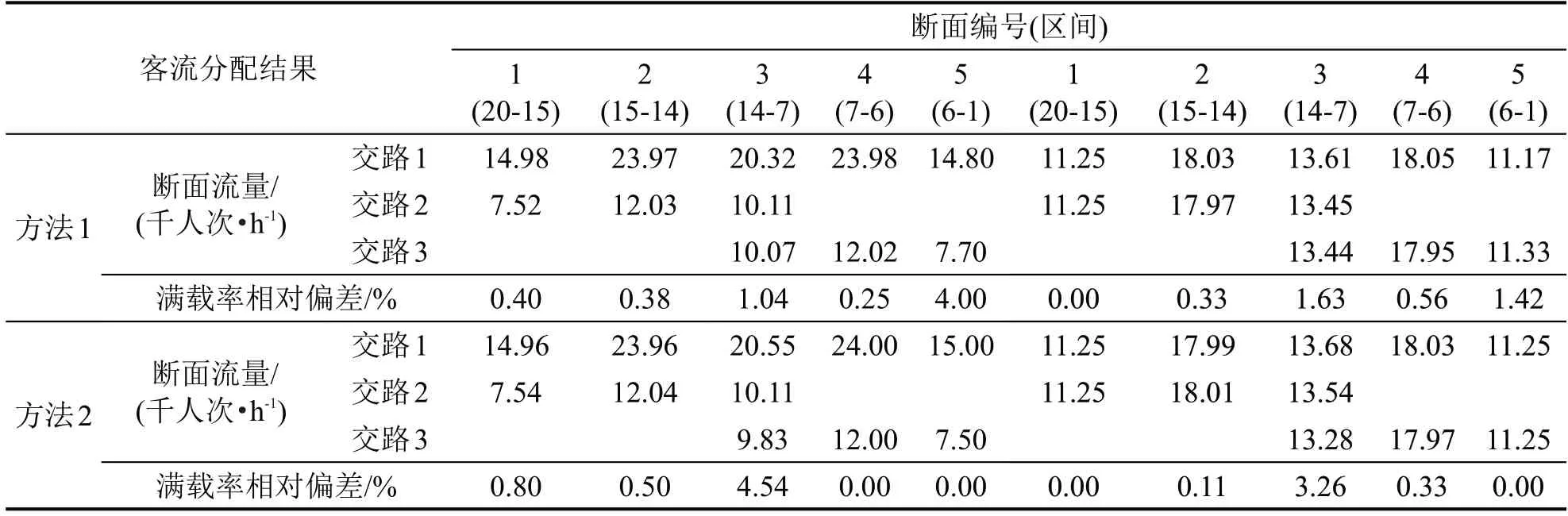
表2 两种客流分配方法的配流结果Table 2 Results of two passenger assignment methods

由表2可知，多编组开行方案下，方法1 和方法2 所得配流结果的满载率相对偏差最大值分别为4.00%和4.54%，两者相差0.54%。造成满载率相对偏差增加的原因在于本文采用的MSA求解方法中的客流加载过程为反馈迭代计算过程，以满足服务网络达到平衡状态。服务网络达到平衡状态时要求网络的总体平衡程度更高，即满载率相对偏差之和更小，而不要求断面的满载率相对偏差是否变化。单一编组开行方案下，满载率相对偏差最大值分别为1.63%和3.26%，两者相差1.63%，可见两种方法满载率相对偏差差异较小，表明两种方法均可以实现运量与运力的较好匹配。但从全部断面的满载率相对偏差之和来看，多编组和单一编组开行方案下，方法1 分别为6.07%和3.94%，方法2 分别为5.84%和3.70%，方法2的相对满载率偏差之和减少0.23%和0.24%。相对满载率偏差值之和越小，说明由分配结果所得的满载率与理论计算满载率越接近，运量与运力的匹配越好，表明网络的平衡程度越高，可见，方法2优于方法1。

造成相对满载率偏差之和减少的原因在于两种客流分配方法的客流加载机制不同。一是，既有基于超路径的客流增量分配方法所达到的平衡状态与客流分割次数和分割比例相关；二是，既有方法的客流加载过程可以认为是一种相对“直接”的方法，即客流加载在完成给定的分割次数后，则停止计算，不论网络是否达到所要求的平衡状态。本文采用的MSA 方法中存在反馈迭代计算过程，若网络未能达到平衡解误差值(收敛判断条件)，则会迭代计算，直至满足收敛条件。因此，本文方法所得结果在客流分布上更加均衡。

6 结论

本文以典型共线运营多交路列车开行方案为基础，构建了基于列车开行方案的客流分配用户均衡模型，并提出了轨道交通多交路共线问题求解算法和客流分配模型的MSA算法，研究结果表明：

(1)本文提出的基于列车开行方案的客流分配方法可以适应多编组和单一编组模式下的多交路共线运营客流分配。算例研究表明，共线区段列车平均满载率与理论计算所得断面满载率最大差值为3.17%，满载率相对偏差最大值为4.54%，可以实现客流需求与列车运力的合理匹配。

(2)相同服务频率下，多编组与多交路组合运营的列车开行方案较单一编组多交路列车开行方案具有更强的客流适应性。多编组运营模式下的最大断面满载率较单一编组的最大断面满载率低15.64%，且各区间满载率更加均衡。因此，在保持发车频率不变的条件下，合理安排列车编组可以使运力与需求更加匹配，且服务水平更高。

(3)与既有客流分配方法相比，本文方法所得的满载率相对偏差最大值虽稍有增加，但多编组和单一编组开行方案下的相对满载率偏差之和分别减少0.23%和0.24%，总体上优于既有方法，可为列车开行方案编制及优化调整提供依据。