基于极限学习机的短期交通流预测混合优化模型

蔡浩，李林峰，李涵，李新*，周腾

(1.汕头大学，计算机科学与技术系，广东汕头 515063；2.海南大学，网络空间安全学院，海口 570228)

0 引言

交通拥堵一直是现代城市面临的重要挑战之一。随着城市化的快速发展和人口的增加，交通流量增长导致道路网络负荷增加，从而导致拥堵、延误和环境污染等问题。解决这些交通问题的关键是准确预测和理解交通流的变化模式和趋势。然而，由于交通流的不确定性和随机性，构建一个合理且稳健的预测模型具有一定的挑战性。在过去的几十年里，交通流预测已经成为交通工程和城市规划领域的研究热点，吸引了大量的学术研究和实际应用。

国内外关于交通流预测模型的研究大致可以分为两类：参数化模型和非参数化模型。首先，参数化模型主要包括自回归移动平均模型(ARIMA)、卡尔曼滤波模型(KF)、灰度模型(GM)等等。例如，Liu 等[1]提出的ARIMA(6,1,6)模型在短期交通流预测方面取得不错成绩，但未考虑短期交通流的非线性和不确定性的特点。Cai 等[2]提出嵌入固定点算法来更新最大熵推导的卡尔曼滤波的后验估计，Guo等[3]提出一种基于灰度模型的短期交通流预测方法，通过引入时间延迟因子和非线性因子来解决交通流存在的延迟性和非线性，以上两种模型是明确的，易于理解的，但它们需要特定的领域知识或专业知识才能发挥作用，不适当的假设或简化可能会降低这种模型在实际应用中的预测精度，特别是对于具有复杂和大规模计算的智能交通系统的实时操作。其次，非参数化模型包括支持向量回归(SVR)、人工神经网络(ANN)、循环神经网络(RNN)、决策树(DT)等等。例如，Fu等[4]建立了基于SVR的短时交通流预测模型，通过引入和函数把交通流预测问题转化为高维空间中的线性回归问题取得不错效果，但参数优化方面存在可提升空间未达到最好效果。Cheng等[5]提出基于随机森林模型的短时交通流预测方法，通过实验验证了其较好的预测精度，且与人工神经网络相比具有参数调节方便、模型训练时间短等优点，但未考虑短期交通流的多样性、不确定性和非线性等特征。Jia等[6]提出一种基于RBF 神经网络的短团队交通量预测新方法，在预测中间交叉口时考虑相邻交叉口的交通流量。Wang 等[7]建立了一种基于深度学习理论的长短时记忆-循环神经网络(LSTM-RNN)交通流时间序列分析及预测框架，降低了样本依赖性，提升了实用性和扩展性，以上两种基于神经网络的模型虽然取得了较高的预测精确度，但其预测精度与时间成本呈正比，更适用于大规模预测，针对短期交通流非线性特征处理不敏感，其预测精度往往受到样本量的限制。

交通流量预测的任务是训练一个网络模型g，其作用是将交通流量数据T准确映射到未来的交通流量数据P，即P=g(T)。然而，在寻找和训练适应所有数据集并都能达到最佳性能的最佳映射函数g*方面存在一些困难。鉴于此，本文提出一种混合优化模型，即一个模型g能够自动确定交通流数据的基本预测模型G中的最佳参数，表示为g*=G(X,g)，其中，X为模型输入参数。从元模型的角度重新考虑学习模型的优化潜力，并通过阿姆斯特丹数据案例进行实验分析以验证其可行性。

1 ASO-ELM 短期交通流预测混合优化模型

本文深入研究了一个短期交通流量预测混合模型，称作ASO-ELM，以该模型为例深入研究混合优化模型在短期交通流预测领域的表现。在极限学习机(ELM)中，由于输入权重和隐层偏差在初始化过程中是随机产生的，其预测精度不理想。因此，本文提出将原子搜索优化(ASO)算法嵌入到ELM 中，在ELM 的随机参数确定过程中，使用ASO 来选择最优参数，以此达到ELM 参数最优状态，提升模型预测精度。

1.1 极限学习机

ELM 是由Huang 等[8]在2004 年首次提出的。ELM 被认为是一种特殊的前馈神经网络(FNN)，ELM相较于传统FNN更加简单、快速和灵活，因其随机生成初始权重不需要进行优化过程，故训练速度更快；且只有一个隐藏层，神经元数量比FNN更少，故更简单。ELM 的结构分为三层，输入层、隐藏层和输出层，如图1所示。

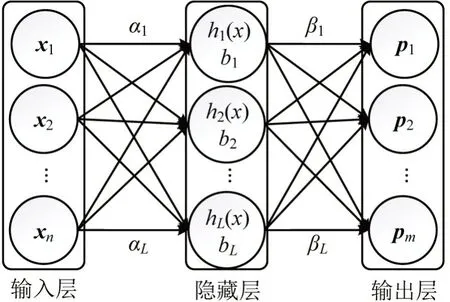
图1 ELM结构图Fig.1 ELM structure diagram

图1 中，xi为第i个输入，i=1,2,…,n，共n个输入；L为隐藏层节点个数；αi为隐藏层节点的输入权重，i=1,2,…,n，bj为第j个隐藏节点的偏置，j=1,2,…,L，两者都是随机产生或人为给定的；hi(x)为隐藏层输出，i=1,2,…,L；pi为第i个输出，i=1,2,…,m，共m个输出。学习过程中只需要通过两者计算隐藏层和输出层之间的连接输出权重βi，i=1,2,…,L，这一特点使它具有较快地学习速度和较高的泛化能力，以及较强的学习和拟合能力。ELM 的实现原理如下：假设有N个样本(Xi,ti)，i=1,2,…,N，Xi为第i个训练样本向量，Xi=[xi1,xi2,…,xin]T∈ℝn，xij为第j个训练样本分量，j=1,2,…,n；ti为第i个数据样本的对应标记，ti=[ti1,ti2,…,tin]T∈ℝm，tij为第j个数据样本分量，j=1,2,…,n。ELM网络可以表示为

式中：g(x)为激励函数；Wj为输入层和隐藏层之间的输入权重矩阵，Wj=[αj1,αj2,…,αjn]T；Wj·Xi为连接权重矩阵与输入矩阵的内积。极限学习机的目的是使输出误差最小化，即预测值与测试值的差值最小，可以表示为

1.2 原子搜索算法

ASO作为一种比较新颖的自然启发性算法，最早由Zhao等[9]在2019年提出，它的基本特征是模拟原子之间的相互运动模型的原子运动规律。在这个算法中，搜索空间中的每一个解都被称为一个“原子”。根据牛顿第二定律，第i个原子的加速度ai与原子之间的相互作用力Fi、原子系统的原子约束力Gi以及原子的质量mi有关，即

(1)Fi定义为第i个原子在第t个时刻受到来自d维空间内其他原子的具有随机权重的分量的相互作用力之和，即视为原子受到的总力，表示为

式中：Kbest为适应度最优的前K个原子组成的集合，o=1,2,…,K，详解见下文；rando为区间[0,1]上的一个随机值；为兰纳—琼斯势数学模型中原子间相互作用势能变化[10]，公式为

式中：σ(t)为长度比例；rij(t)为两原子之间的欧几里得距离；ε(t)为势能。

(2)Gi为原子系统中共同作用在第i个原子的约束力，其在d维空间的表达式为

式中：δ为原子系统中的乘数权重；为第t次迭代中种群最佳原子位置，即搜索空间内的最优解；为原子第n次迭代的当前位置解；T为最大迭代次数

(3)原子加速度ai，其在d维空间的表达式为

式中：Mi(t)为第t次迭代时第i个原子的函数适应值；Ffit,i(t)为第t次迭代时第i个原子的适应度值；Ffit,best(t)和Ffit,worst(t)分别为第t次迭代时具有最小适应度、最大适应度的原子的适应度值。

最后，第t+1 次迭代时第i个原子的速度和位置分别为

为了增强算法初期的空间探索能力，保证每个原子与尽可能多的原子进行交互，使其适应度值与其K个相邻的原子相近。而在迭代的最后阶段，反之，使其尽可能的收敛到最优位置，且其K个邻居具有更好的适应度值。因此，K随着迭代而逐渐减小，即

1.3 模型构建

ASO-ELM 模型在ELM 的基础上整合了ASO框架，以迭代的方式找到ELM 的最优输入权重矩阵和隐藏层偏置，通过计算ASO 每次迭代的适应度值，找到优化ELM 参数的最优方案，ASO-ELM的工作流程如图2所示。

图2 ASO-ELM工作流程图Fig.2 ASO-ELM workflow diagram

2 算法设计

ASO-ELM的训练步骤如表1所示。在算法开始，进行初始化操作，包括建立ELM网络和初始化ASO算法。首先，对于ELM部分，有两个主要参数需要初始化或选择，即激活函数f(x)和隐藏层的节点数L。在ASO算法中，初始化群数量N、最大迭代次数T、解空间上下界等参数，其中解空间大小由ELM输入矩阵W和隐含层参数矩阵B决定。

表1 ASO-ELM算法Table 1 ASO-ELM algorithm

3 案例分析

实验数据来自阿姆斯特丹A10 环形公路的4个交汇路口，通过路边单元(Roadside Units,RSU)对兴趣点(Point Of Interest,POI)，即4 个路口的交通流量进行采集，RSU实时将这些数据传输到智能交通控制中心。

3.1 数据描述

这些真实数据由Wang 等[11]收集，数据收集地点分别在阿姆斯特丹A10 环形主干道的交汇路口A1、A2、A4 和A8。数据采集时间为2010年5月20 日～6 月24 日，通过RSU 在4 个道路交汇口进行每1 min 的数据采集，这些数据代表了当时路口的车辆数量，因其真实体现交通流的时间属性成为本文实验数据的首选方案。其中，A1、A2、A4作为连接城市的主要路口，车流量较多，聚合数据最多可达到5000辆；A8路口连接郊区，因此路口车流量较少。在原始数据中，共有50400 条车流量数据，其中存在一些错误的数据是0或负数，本文用不同日期同一时间的测量平均值来替换错误的数据，以改善训练样本。

3.2 模型处理

短期交通流预测的重点不是每分钟车辆数量的起伏，而是有一定时间间隔的时期。因此，根据原始数据中每1 min的汇总数据计算出每10 min的数据平均值，经过预处理后作为输入模型的样本数据XT=[x1,x2,…,xZ]，其中，Z为每个10 min的聚合时刻，xZ为Z时刻该路口的车辆数量，处理后的数据共5040 条。将输入的样本数据分为两部分：第一部分是训练数据，包括前4 个星期的数据；第二部分是测试数据，即最后一周的数据。为了保证预测精度的可靠性，模型采用交叉验证法处理输入样本，如图3所示。

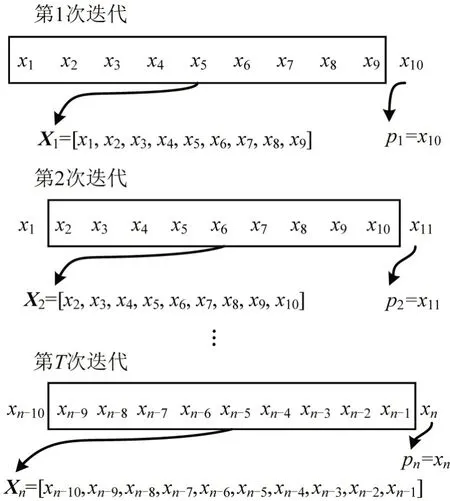
图3 交叉验证法处理输入数据Fig.3 Cross-validation method to process input data

此外，ASO-ELM 模型选择的激活函数为sigmoid 函数，并通过实验结果将ELM 的隐藏层设置了40 个神经元节点。如表2 所示，当ELM 神经元L=40 时模型的实验评估标准，即MAPE值小于神经元节点，与L=50 时的MAPE 值几乎一致，耗时却比其更低。短期交通流预测需要短时间高精度的预测，所以舍弃L=50 和L=60，本文选择40 个神经元节点。平均绝对百分误差(Mean Absolute Percentage Error,MAPE)为实验评估标准之一，后文中将详细说明。

表2 不同节点数的ASO-ELM下MAPE和时耗对比Table 2 Comparison of MAPE and time consumption under ASO-ELM with different number of nodes

其次，本文设置200次的迭代实验，即T=200，如图4 所示，当迭代次数超过200 次时模型的收敛程度趋于稳定。

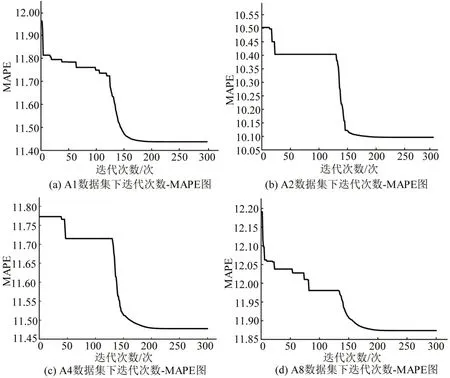
图4 ASO-ELM迭代收敛图Fig.4 ASO-ELM iterative convergence graph

本实验中设定的ELM参数均合理，ASO-ELM的详细参数设置如表3所示。

表3 ASO-ELM详细参数设置Table 3 Detailed parameters setting

3.3 预测评估指标

短期交通流预测问题作为线性回归问题之一，常见的回归评估指标包括：平方根误差(Root Mean Square Error,RMSE)、平均平方误差(Mean Square Error,MSE)、平均绝对百分误差(Mean Absolute Percentage Error,MAPE)等。本文采取的指标之一是RMSE，其通过对MSE 的开方解决了MAE 函数不光滑等问题的缺陷；另一个指标是MAPE，MAPE 相较于RMSE，拥有更强的鲁棒性，不易受个别离群点影响；本文还使用R2(R-squared，也称决定系数)评估指标对同类优化模型的比对，祥见后文。本文侧重对比MAPE，RMSE 则作为辅助评估指标。MAPE和RMSE的计算公式为

式中：EMAPE为MAPE值；ERMSE为RMSE值；p(i)为模型预测值；为测试真实值；N为样本总数。

3.4 预测结果分析

通过比较其他常见的回归模型在4 个相同数据集下的性能表现来评估ASO-ELM 模型，并通过MAPE和RMSE评估指标来反映，指标结果均是经过调优的模型结果。如表4和表5所示，其中，记录的数据是常见的回归模型在A1、A2、A4 和A8 这4个数据集下训练100次得到的评估指标的平均值。

表4 4个数据集下不同预测模型的MAPETable 4 MAPE of different forecasting models under four datasets (%)

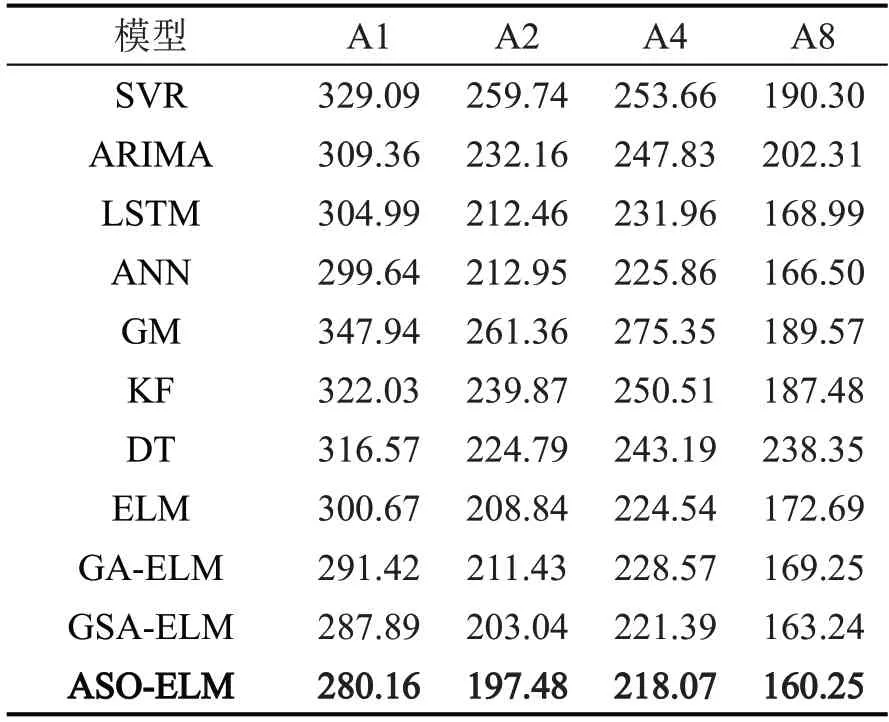
表5 4个数据集下不同预测模型的RMSETable 5 RMSE of different forecasting models under four datasets (veh·h-1)

从表4和表5可以看出：第一，在传统优化模型ELM与非参数化模型(如SVR、ANN、LSTM、DT)的比较中，前者的实验评估指标MAPE和RMSE值更低，说明其预测精度更好，这主要得益于作为参数化模型的ELM在小数据样本的实验环境中拟合效果和实验效果更好；第二，传统优化模型ELM与参数化模型(如KF、GM、ARIMA、ELM)相比，前者成绩也更优，这主要归功于ELM 拥有非参数化模型的特点，因其更为简单的神经网络结构使得ELM更加灵活，其学习速率能更快适应更多的分布，故而训练得到的效果更佳；第三，ASO-ELM模型在传统ELM 模型特殊结构的基础上，拥有ASO 优化算法的加持，取得的实验评估指标成绩最好，在同样的4个数据集下，其MAPE指标较传统ELM模型分别下降了6.88%、6.20%、9.43%和8.66%，与其他非混合优化模型相比，混合优化模型的预测精度都远超过非混合优化模型。

针对发展势头正盛的人工神经网络(ANN)作进一步分析，ASO-ELM 的MAPE 值分别降低了11.97%、11.11%、12.33%和8.30%，RMSE 值分别降低了6.50%、7.26%、3.45%和3.75%，这归功于ELM仅仅通过计算而得出训练结果的特殊训练模式。尽管从表4和表5中看似ELM模型和ANN模型的性能差别不大，但实验中的ANN 模型是已经经过调优的结果且其训练时间远超于传统ELM 模型。对于ANN模型，ASO-ELM模型除了在评估指标中体现出数值优势之外，还包括：

(1)由于ASO-ELM 的输入层和隐藏层的连接权重W和隐藏层的偏置阈值B可以随机确定，确定后不需要调整，那么确定β的过程就是解方程一次确定的过程，这使得ASO-ELM 的学习速度明显高于ANN。

(2)ASO-ELM模型不需要克服传统ANN网络的常见问题，如陷入局部最优、梯度消失等，只需要关注ASO-ELM 模型中隐藏层节点个数对于模型的影响，这使得ASO-ELM模型的网络结构比ANN简单的多。

(3)ASO-ELM 模型可以使用几乎所有的非线性激活函数和几乎所有的分段连续函数，包括不连续、微分和非微分函数等，而ANN就不适用非微分函数。

总的来说，ELM模型是一种简单、高效和泛化能力更强的ANN 模型，针对短期交通流的动态性特征，其高效的学习速度更为适用。

实验还比较了不同优化算法下混合优化模型的不同性能，如GA-ELM 模型和GSA-ELM 模型。GA-ELM 利用遗传算法对ELM 进行优化，GSAELM 则使用引力搜索算法进行优化，两者皆旨在将传统ELM 存在的优化空间用优化算法进行优化，使其得到更良好的性能表现。如图5 所示，在相同的4 个数据集下，ASO-ELM 模型的MAPE 值都低于前两者，并且在RMSE 评估指标中，ASOELM模型取得的成绩与GSA-ELM相匹配，并保持微弱领先，主要得益于ASO 作为近些年开发的优化算法，其性能较GA、GSA更优。

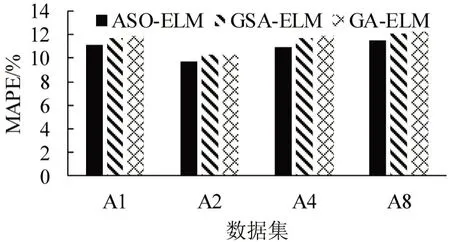
图5 3种优化ELM的MAPE对比Fig.5 MAPE comparison chart of three optimized ELMs

此外，还比较了3 种模型在R-square 评估指标中的表现，如表6 所示。其中，ASO-ELM 模型的R-square 值更接近于1，表明ASO-ELM 模型的模型参数对预测值的解释能力更强，即对样本数据的拟合效果更好。因此，ASO-ELM 具有更好的预测精准度。

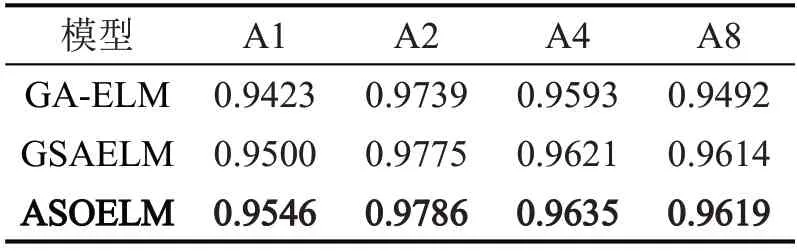
表6 3种优化ELM的R-square决定系数Table 6 R-square decision coefficients of three optimized ELMs

图6为ASO-ELM模型的预测值与测试集中的实际值的相对误差，其计算公式为

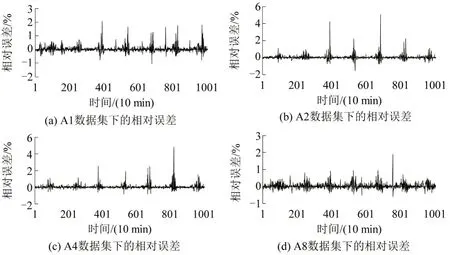
图6 ASO-ELM模型的相对误差Fig.6 Relative error of ASO-ELM mode

4 结论

本文基于短期交通流动态性、非线性等造成短期交通流预测困难的特征，选取极限学习机和原子优化算法作为本文的方法支撑和理论基础，结合两者特点构建短期交通流预测的混合优化预测模型ASO-ELM，探讨混合优化模型在短期交通流预测领域的潜力，通过与既有的短期交通流预测模型方法进行对比实验，得到主要结论如下。

(1)实验结果表明，ASO-ELM混合优化模型取得了最优的评估指标，主要得益于ELM 简单的神经网络结构和仅仅通过计算而得出训练结果的特殊训练模式。此外，ASO-ELM相较于ELM拥有更准确的预测精度，但不缺失ELM训练速度快、灵活等优点，表明混合优化方法对传统ELM 模型的预测精度提升明显。

(2)实验还比较了同样理念下混合优化模型之间不同优化算法的性能区别，包括GA-ELM、GSAELM、ASO-ELM 的评估指标仍然优于其他两者，主要得益于ASO 作为近些年开发的优化算法，其性能较GA、GSA 更优，表明混合优化模型的预测效果或预测性能受到优化算法的性能影响，更优的优化算法能够释放预测模型的潜力。

(3)ASO-ELM 模型预测数据与真实测量数据进行对比分析，使用相对误差等评价指标，得出评价相对误差维持在5%以内；最大相对误差为4.83%，进一步验证了模型预测的准确性，研究结果为构建短期交通流预测模型提供理论依据，对缓解道路拥堵具有重要意义。