晶体结构中一个高考新热点探析——晶胞中原子的投影及运用

汤 伟(正高级教师、特级教师)

(安徽省灵璧中学)

在“物质结构与性质”的考查中,几乎年年都会遇到对晶胞结构的考查,该考查点能够较好地体现“宏观辨识与微观探析”“证据推理与模型认知”等化学核心素养.近年来,随着新课标、新高考的逐步实施,我们研究高考试题可以发现,2023 年的全国乙卷、浙江卷、湖北卷、海南卷,2022 年的广东卷、湖南卷,2021年的湖北卷,2019 年的全国新课标Ⅰ卷与新课标Ⅱ卷均涉及关于晶胞中原子的投影问题,可见关于原子投影问题在逐渐成为高考的新热点.下面我们针对该问题进行分析探究.

1 原子投影的基本规律

判断晶体或晶胞中一些原子的相对位置,有时候较为抽象,为便于分析,对于三维空间立体结构中原子间的相对位置,我们常常采用“降维”处理,即通过原子在某个平面上的投影,由此辅助确定原子的相对位置及数量的多少,从而准确分析推理晶胞的相关问题.

针对原子投影后的结果,我们要根据命题者的要求,仔细分析投影时所选择的坐标轴方向.常见原子在某平行四边形的投影,可能在矩形或四边形的顶点、边的中心、面的中心、4个小正方形的中心等.比如,下面几种常见的晶胞,若不同原子均沿着z轴方向投影,所得到的结论(或规律)如下.

1)晶胞的8个顶点原子沿z轴方向投影,如图1所示.

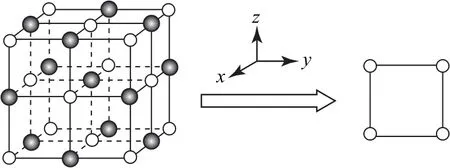
图1

2)晶胞上4 个棱心原子(图2 中①②③④号原子)沿z轴方向投影(与8个顶点原子投影重合),如图2所示.

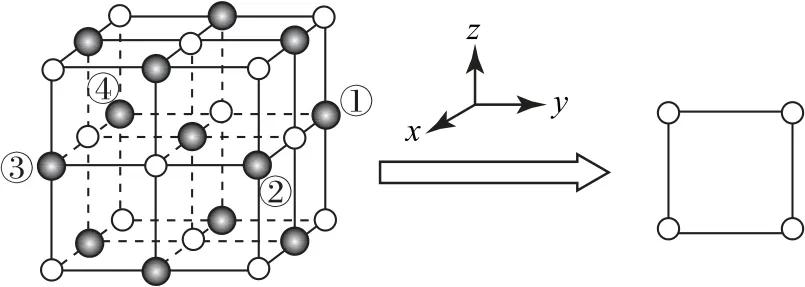
图2

3)晶胞上12个棱心原子沿z轴方向投影(与8个顶点原子投影重合),如图3所示.

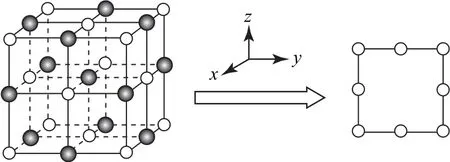
图3

4)晶胞的6个面心原子沿z轴方向投影(若有棱心原子,则会与部分棱心原子投影重合),如图4所示.

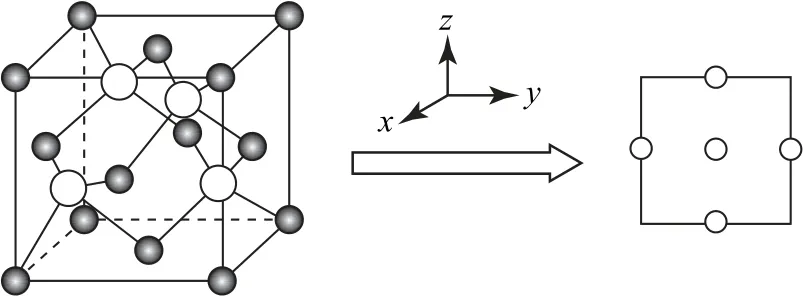
图4

5)晶胞的1个体心原子沿z轴方向投影(若有面心原子,则会与上下面的2个面心原子投影重合),如图5所示.

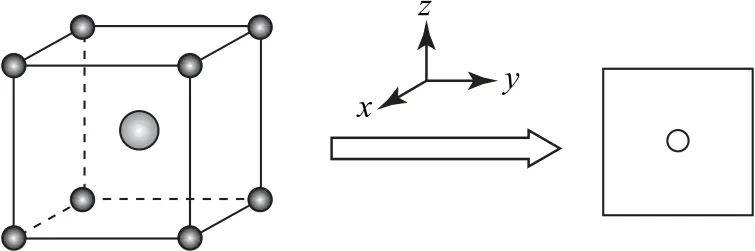
图5

6)晶胞处于8个立方体中心的8个原子沿z轴方向投影),如图6所示.

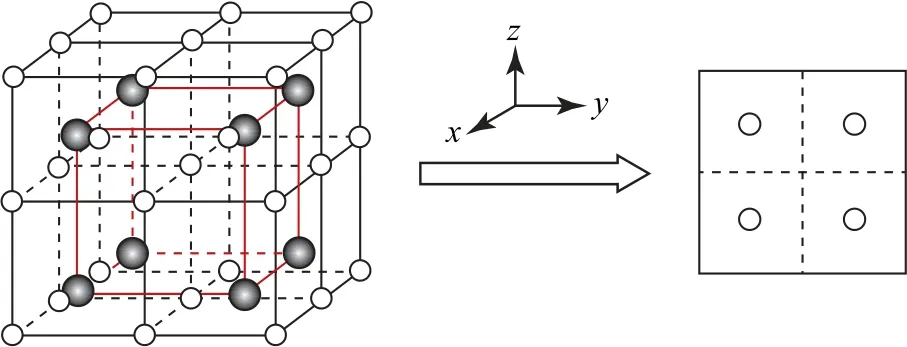
图6

7)晶胞处于1/4或3/4处的原子沿z轴方向投影(与8 个立方体中心原子投影部分重合),如图7所示.

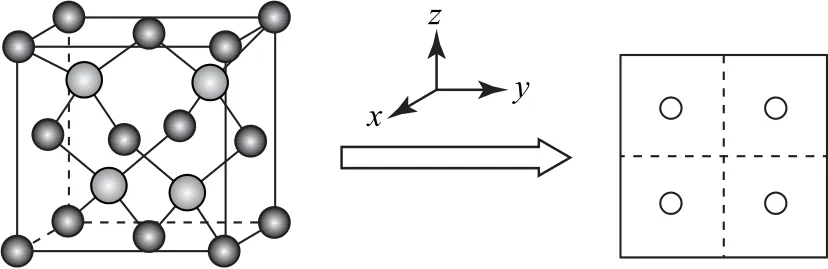
图7

2 原子投影知识点的具体运用

借助原子投影知识,可以较好地帮助我们理解晶体或晶胞中一些原子的相对位置,该类知识点的考查常常借助“降维”或“升维”处理,如2023年全国乙卷第35题、2023年湖北卷第15题、2023年6月浙江卷第17题,均采用“降维”处理,使考生便于分析推断晶胞中原子的相对位置;2022年湖南卷第18题,则是通过“升维”处理,增加了思维的深度,由投影推断未知晶体结构.为使大家更加熟悉并能灵活运用该类知识点,下面我们以近年高考试题为例进行分析说明.

*本文为江苏省社会科学基金项目“芥川龙之介《中国游记》中的江苏书写研究”（编号：14WWD001）的阶段性成果。

例1(2023年全国乙卷,节选)一种硼镁化合物具有超导性能,晶体结构属于立方晶系,其晶体结构、晶胞沿c轴的投影如图8 所示,晶胞中含有____个Mg.该物质的化学式为______,B—B 的最近距离为______.

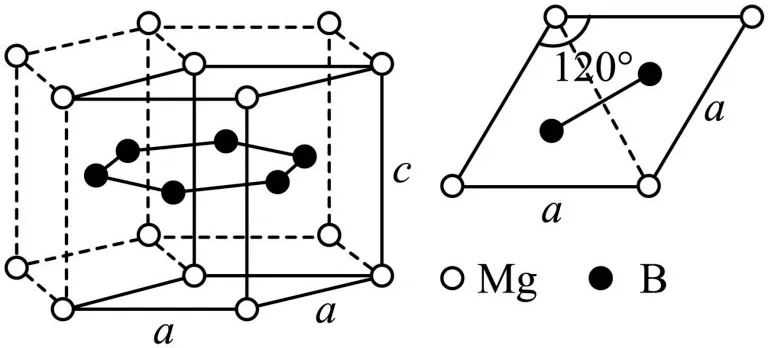
图8

例2(2023年湖北卷)镧La和H 可以形成一系列晶体材料LaHn,在储氢和超导等领域具有重要应用.LaHn属于立方晶系,晶胞结构和参数如图9所示.高压下,LaH2中每个H 结合4 个H 形成类似CH4的结构,即得到晶体LaHx.下列说法错误的是( ).

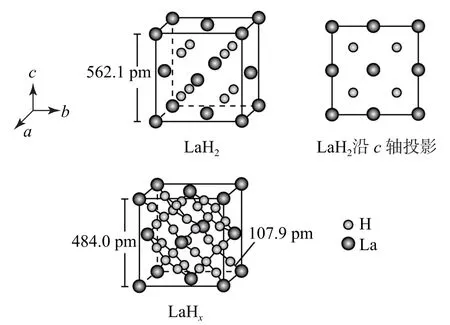
图9

A.LaH2晶体中La的配位数为8

B.晶体中H 和H 的最短距离:LaH2＞LaHx

C.在LaHx晶胞中,H 形成1个顶点数为40的闭合多面体笼

D.LaHx单位体积中含氢质量的计算式为

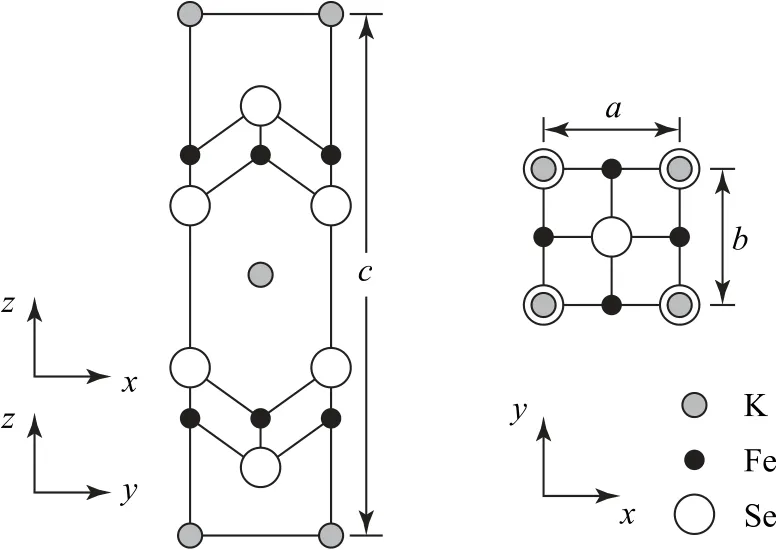
图10

例4(2021年河北卷,节选)分别用○、·表示H2PO—4和K＋,KH2PO4晶体的四方晶胞如图11-甲所示,图11-乙、图11-丙分别显示的是H2PO—4、K＋在晶胞xz面、yz面上的位置.

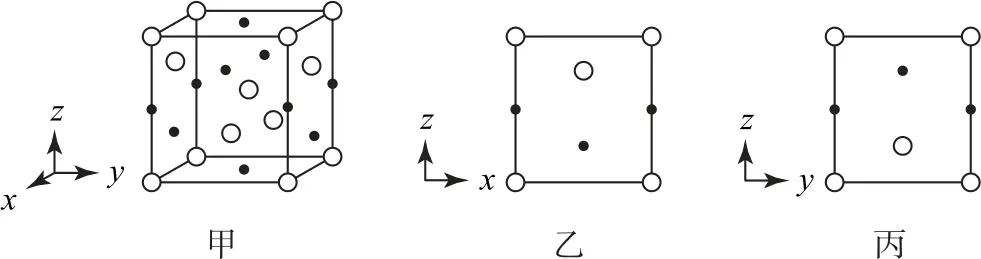
图11

(1)1个晶胞中K＋和的单元数为____.(改编)

(2)晶胞在x轴方向的投影图为____(填标号).

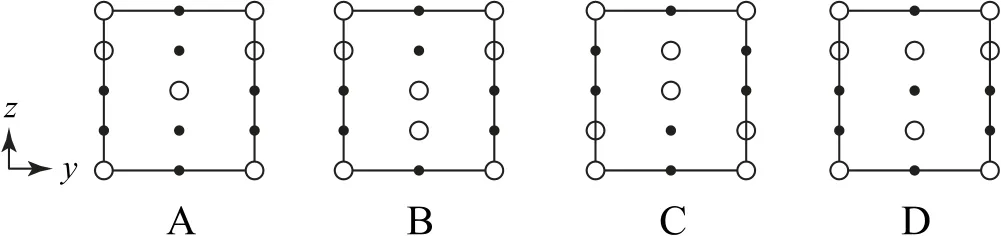
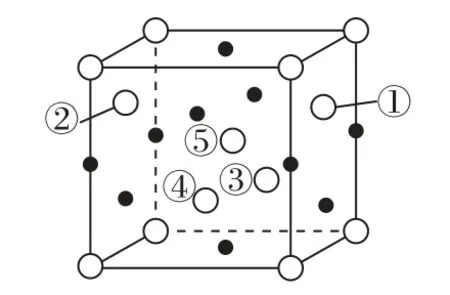
图12

图13

3 “另类”投影在测试中的呈现

关于晶胞中原子的投影问题,旨在通过三维到二维、二维到三维之间的转换,考查学生空间想象能力与逻辑推理能力.为强化学生的理解与运用能力,考查原子的投影问题时,有时候还会设计成沿着某个夹角或体对角线、面对角线“投影”,我们暂且称之为“另类”投影,预计这也是一种考查方式.

例5(2019年全国新课标Ⅰ卷,节选)图14-甲是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu.图14-乙是沿立方格子对角面取得的截图.可见,Cu原子之间最短距离x＝_________pm,Mg原子之间最短距离y＝_________pm.设阿伏加德罗常数的值为NA,则MgCu2的密度是_________g·cm—3(列出计算表达式).

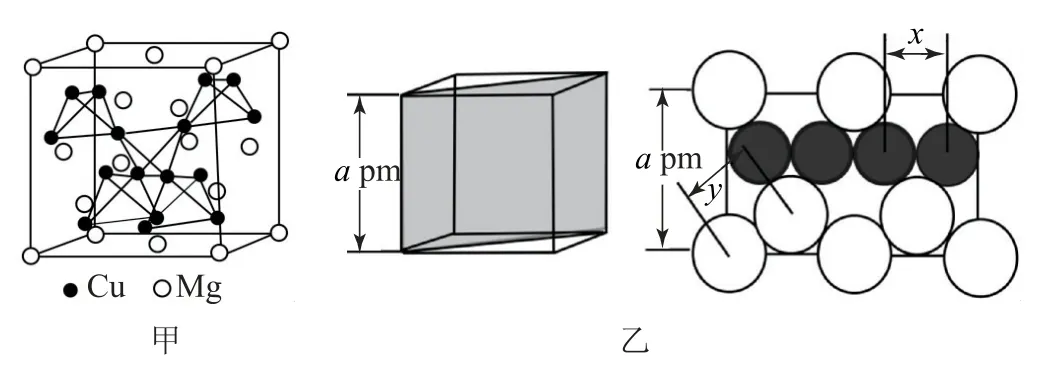
图14

例6若磷化硼晶胞(如图15-甲)沿着体对角线方向的投影(图15-乙中虚线圆圈表示P 原子的投影),用实线圆圈画出B原子的投影位置(注意原子体积的相对大小):_______.

图15

(完)