关联运动说关联
马仕彪
(安徽省濉溪中学)
关联运动是指物体间通过一定的连接方式,从而使其运动发生联系的运动.弄清楚关联运动所关联的物理量是理解关联运动的最基本的要求,也是最有效的方法.关联运动的实质是运动的合成与分解,而矢量的合成与分解满足平行四边形定则或三角形定则.本文主要从关联运动关联的角度进行多维度研究,以真正理解关联的思想.
1 从一个经典关联运动模型说起
模型A、B两物体通过细线按照如图1所示的方式连接,某时刻细线OA与水平方向的夹角为α,A的速度为vA,B的速度为vB,请讨论vA与vB之间的关系.
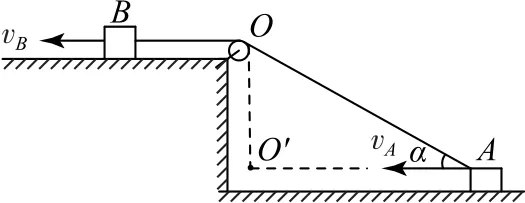
图1
方法1运动效果法
如图2所示,A的实际运动方向向左,即A的合运动方向向左,由于A的运动产生两个效果,其一是使细线OA变短,其二是围绕O点转动,因此可以将vA沿着细线和垂直细线方向进行分解,分量分别为v∥=vAcosα,v⊥=vAsinα,而B的速度vB恰好沿细线方向,因为细线总长度一定,所以有vB=v∥=vAcosα.

图2
方法2机械能守恒法
因为A、B两物体组成的系统满足机械能守恒定律,细线对系统做功代数和为零,即细线对A、B两物体做功功率大小相等,由功率定义有FvAcosα=FvB,化简得vB=vAcosα.
方法3极限位移法
如图3所示,从初始位置经过极短时间Δt内,△OO″A′近似为等腰三角形,即OO″≈OA′,细线OA缩短了ΔxOA=xOA—xOA′=vAΔtcosα,细线OB伸长了ΔxOB=vBΔt,由于细线总长度不变,所以满足ΔxOA=ΔxOB,化简有vB=vAcosα.

图3
方法4数学思想法
如图4所示,对初状态应用勾股定理,有

图4
对经过极短时间Δt时应用勾股定理,有
两式相减,有
2 应用举例
例1如图5所示,连杆AB、OB可绕图中A、B、O三处的转轴转动,连杆OB在竖直面内的圆周运动可通过连杆AB使滑块A在水平横杆上左右滑动.已知OB杆长为R,其绕O点以角速度ω做逆时针方向的匀速转动,当连杆AB与水平方向夹角为α、AB杆与OB杆的夹角为时,求滑块A的速度vA.

图5
如图6所示,A、B两者的速度沿杆AB方向的分量相等,而B的合速度为圆周运动的线速度vB=ωR,方向与OB相垂直,因此有vAcosα=

图6
方法2数学思想法
如图7所示,设杆AB的长度为L.对初状态应用余弦定理,有L2=R2+AO2—2R·AOcos[π—(α+β)].经过极短时间Δt时,仍应用余弦定理,有

图7
两式结合有
化简得
化简有
讨论与总结
1)当β=180°,α=0°时,即B处于AO之间,此时vA=0,A运动到最左端;
2)当β=0°,α=180°时,即O处于AB之间,此时vA=0,A运动到最右端;
3)当β=90°时,即AB与OB垂直,此时A的速度最大,最大值为;
例2如图8 所示,质量均为m的小球甲、乙用一长为L的细杆相连,甲球靠在光滑竖直墙面上,乙球置于光滑的水平地面上.开始时,杆与水平面的夹角为60°.释放后甲球沿竖直墙面下滑,乙球右滑,当细杆滑至与水平面成θ角时,甲刚好离开墙壁,求此时的θ角和乙的速度.
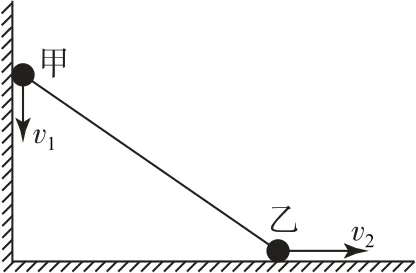
图8
令
将K对θ进行求导有
例3如图9所示,滑块A、B的质量均为m,A套在倾斜固定的直杆上,倾斜杆与水平面成45°角,B套在水平固定的直杆上,两杆略分离不接触,两直杆间的距离忽略不计,两直杆足够长,A、B通过铰链用长度为L的刚性轻杆(初始时轻杆与水平面成30°角)连接,将A、B由静止释放,不计一切阻力,滑块A、B可视为质点,重力加速度为g,下列说法正确的是( ).
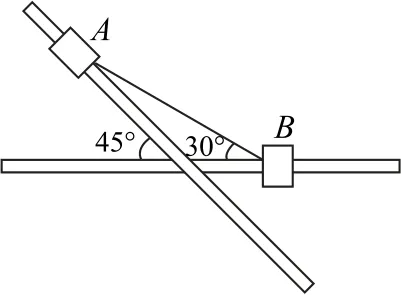
图9
A.A、B及轻杆组成的系统机械能守恒
B.当A到达B所在的水平面时,A的速度为
近年来,通信传输网络技术发展迅速,新技术层出不穷。日新月异的通信技术为建设坚强可靠的电力通信传输网创造了条件。目前,通信业界采用的传输网技术体制主要有 SDH,DWDM,ASON,OTN,PTN等。目前,国内地市电力通信网仍以 SDH 网络为主。
C.B到达最右端时,A的速度等于
D.B的最大速度为
其中vAcos45°=vB,解得A的速度为,因此选项B 错误;B滑块到达最右端时,其速度为零,此时轻杆与斜杆垂直,如图10所示.由系统的机械能守恒定律有

图10
解得A的速度为,因此选项C正确.
如图11 所示,当轻杆与水平杆垂直时B的速度最大,此时A的速度为零,由系统机械能守恒定律有,解得B的最大速度为,因此选项D 正确.

图11
例4如图12所示,长度为L的竖直轻杆上端连一质量为m的小球A,杆的下端用铰链接于水平面上的O点.小球A与置于同一水平面上的质量为M的立方体B恰好接触.现轻微扰动,使杆向右倾倒,各处摩擦均不计.某时刻杆与地面夹角为θ时,A、B恰好分离.求A与B的质量比.

图12

图13
例5如图14所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0,方向与绳相垂直.小球相互碰撞时为弹性碰撞,轻绳不可伸长.求:
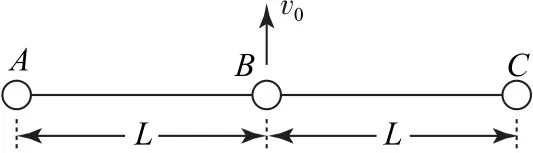
图14
(1)当小球A、C第一次相碰时,小球B的速度;
(2)当三个小球再次处在同一直线上时,小球B的速度;
(3)当三个小球再次处在同一直线上时,绳中的拉力F的大小;
(4)运动过程中小球A的最大动能Ek和此时两根绳的夹角.
(2)当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律有
(3)小球A、C均以半径L绕小球B做圆周运动,当三个小球处在同一直线上时,以小球B为参考系,小球A(C)相对于小球B的速度均为
(4)当小球A的动能最大时,小球B的速度为零.如图15所示,设此时小球A、C的速度大小均为μ,由机械能守恒定律有,小球A的最大动能,结合可得,此时μ=.设此时两绳之间的夹角为θ,由关联运动特点可知μ与AB和BC方向相垂直,由动量守恒定律有,结合可得,因此时两根绳间夹角为θ=90°.

图15
3 结语
在关联运动中,一般只分解合运动,合运动即物体的实际运动,然后再找到运动之间的联系即可,而关联一般表现在沿绳或沿杆的分速度相等.以关联为突破口,理解了关联运动关联的意义,便可以将问题顺利解决.
(完)

