圆周运动中临界问题常见题型分析

靳云雷

(山东省章丘中学)

圆周运动是运动学知识体系中的一个重要分支,与其相关的临界问题则是各类考试考查的热点.本文总结圆周运动中常见的几类临界问题,以促进学生对相关问题的理解和掌握.

1 水平面圆周运动

1.1 水平转台模型

水平转台模型中,临界问题一般与摩擦力有关.随着转速的逐渐增加,物体所受摩擦力也会逐渐增加.当在某一转速下,静摩擦力达到最大值,此时物体则处于临界状态,继续提高转速物块会发生相对运动.而解答这类问题的关键,则是对临界情况进行准确的受力分析.

例1如图1所示,水平转台上,细绳连接质量均为m的A、B两物块,沿半径放置,细绳恰好伸直.A、B距轴心O分别为R和2R,物块与转台间最大静摩擦力为重力的k倍.请作出随转台角速度ω的增加,A、B所受静摩擦力FfA、FfB随ω2的变化图像.

图1

,此时,A所受摩擦力为.此后,绳子产生张力,B所受摩擦力仍为kmg,对A有FfA—FT＝mω2R;对B有kmg＋FT＝mω2·2R.联立可得FfA＝3mω2R—kmg.

当ω继续增大,FfA也逐渐增加,当FfA＝kmg时,A、B与转台达到相对静止的临界点,ω再增加,则会出现相对滑动,设此时角速度为ω2,则有kmg＝,可得

A、B所受静摩擦力FfA、FfB随ω2的变化图像如图2、3所示.

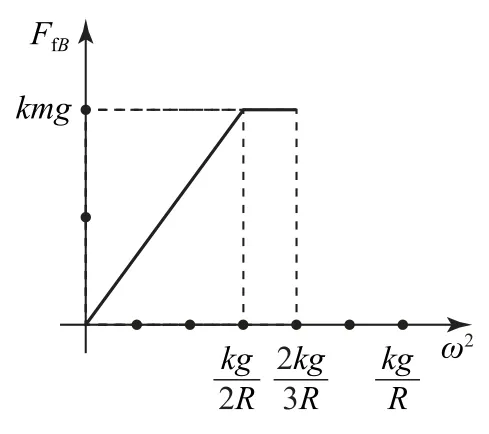
图3

1.2 圆锥摆

在圆锥摆模型中,一般由绳子拉力与重力的合力提供向心力,而随着圆锥摆的变形,其向心力大小也会发生改变.这类问题的临界状态一般出现在绳子拉力最大时.

例2如图4所示,AB为竖直转轴,细绳AC、BC结点C系有质量为m的小球,两绳能承受的最大拉力均为2mg,AC、BC均伸直时,∠ABC＝90°,∠ACB＝53°,BC＝1m,ABC能够绕AB旋转,C做匀速圆周运动.当转速过快时,AC、BC会被拉断,求AC、BC断裂时小球的线速度.

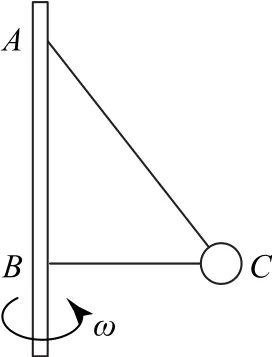
图4

图5

分析可得:FAC与ω无关,说明两绳拉紧后、未断前AC上为恒力,即BC先断裂,由FBC＝(ω2—7.5)m(N)可知,当FBC＝2mg,即＝27.5rad2·s—2时,BC断裂,此时断裂后,小球重力与AC拉力的合力提供向心力.

2 竖直面圆周运动

2.1 最高(低)点临界问题

解答这类临界问题,一般要分析物体在圆周运动过程中到达最高点时的运动状况.根据情况不同,可以进一步分为“绳球模型”与“杆球模型”.“绳球模型”中,在最高点的临界状态,由重力提供向心力,即,则当时,可以到达最高点.“杆球模型”临界条件中,最高点时,杆所受弹力与重力相等,即,则当v≥0时,可以到达最高点.在面对这类问题时,应当厘清题目模型及临界情况,从而进行解答.

例3如图6 所示,长为L的两段绳,一端分别固定在等高的A、B两点,另一端连接质量为m的小球,A、B间距为L.小球做圆周运动在最高点速度为v时,两段绳中张力恰好为0.求当小球运动到最高点的速度变为2v时,每段绳的张力.

图6

2.2 脱轨(不脱轨)问题

不脱轨问题可以根据题目情境分为“内轨模型”与“外轨模型”两类.“内轨模型”中,小球在轨道外侧运动,受到轨道的支撑.当小球经过最高点仅由重力提供向心力时,得,而后小球脱离轨道做平抛运动.“外轨模型”中,要使小球不脱离轨道,最高点速度为其临界状态.同时,经过最低点的速度,临界速度为.当小球在最低点的速度,运动轨迹不超过圆心,也不脱离轨道.当最低点速度时,小球在运动至圆心平面以上某处后脱离轨道做斜上抛运动.细绳模型与其相似.

例4如图7所示,在半径为L的圆形轨道中,有细绳长为L,一端固定在圆心O点,一端连接一小球(视为质点),小球在最低点A时,给其一个的水平初速度,求小球脱离轨道后能到达的高度.

图7

如图8所示,设在图中B点脱轨,此时绳子张力为0,由重力径向分力提供向心力,设绳子与水平夹角为θ,有mgsinθ＝,从A到B,由动能定理得

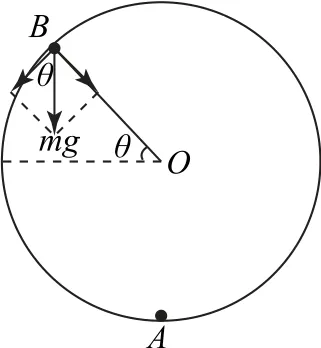
图8

小球脱轨后做斜上抛运动,运动至最高点时速度为vB的水平分量,由机械能守恒定律有

综上所述,本文总结了圆周运动中几类常见的题型,并分析其解题思路,为师生提供参考.要想快速解答问题,需要学生对解题思路、知识等进行总结,以此提升解题效率.

(完)