谐波减速器扭转模态测试技术研究

巩潇 梁学修 葛耀谋 余娴 王磊 赵飞

（1 中国软件评测中心（工业和信息化部软件与集成电路促进中心），北京，100048；2 西安交通大学，西安，710049）

0 引言

谐波减速器的动静态特性直接影响其传动性能。为了优化和提升谐波减速器性能，开展谐波减速器的动静态特性测试方法研究，研究谐波减速器动静态测试技术，开发高性能、高集成度的谐波减速器动静态特性测控系统，就显得十分必要。

目前，谐波减速器的测试方法、技术和指标不够完善。其中，常规性能测试主要有传动效率、静态刚度等，以动态传动精度、稳定性、模态参数等为代表的动态特性涉及较少[1-2]。以协作机器人为代表的新型机器人，在3C电子、新能源等先进制造领域有着巨大的应用潜力[3-4]。这类机器人对减速模块的动态精度和稳定性等有着更高的要求。而传统基于大量静态特性的测试分析，已经不能满足新一代机器人对谐波减速器动态性能的需求，需要对谐波减速器的动态传动精度、模态参数等动态特性开展测试分析研究，以支撑其性能的优化提升。另外，现有谐波减速器测控系统的环境兼容性、通用性较低，不能同时满足多项指标的测试要求，经常需要搭建新的环境，频繁更换测速器。

比利时鲁汶大学（University of Leuven）的TJAHJOW IDODO 等[5]搭建了一种谐波齿轮传动测试实验台，实验设备整体设计较为简单，主要包括电涡流传感器、直流电机和角度编码器等主要零部件。基于搭建的测试实验台，TJAHJOWIDODO 等开展了减速器输入、输出轴的扭转刚度测试，同时采用Maxwell-slip 模型完成了对谐波减速器迟滞特性的量化建模。

美国莱斯大学（Rice University）的GHORBEL 等[6-8]构建了由输出端编码器、待测谐波减速器、惯性负载、扭矩传感器和伺服电机等核心零部件组成的谐波减速器动静态特性测试装置。基于搭建的测试系统，采用Fourier级数法建立了谐波传动静态传动误差的量化模型，实现了对谐波减速器静态传动误差的分析，同时采用遗传积分算法，完成了对谐波减速器非线性静刚度与迟滞特性的建模与分析。

日本谐波传动系统有限公司（Harmonic Drive Systems,Inc.）[9-10]多年来致力于谐波齿轮减速器研发与制造，在国际上具有极高的声誉。该公司一直重视谐波减速器动静态特性的测试工作，研发了谐波减速器动静态测试系统，对谐波减速器开展了刚度、运动平稳性、效率、寿命等多项动静态特性的测试分析，为谐波减速器的动静态性能优化奠定基础。

美国阿贡国家实验室（Argonne National Laboratory）的PREISSNER 等[11-12]搭建了谐波减速器动静态特性测试装置，采用不同的加载方式完成了对谐波减速器静刚度特性的测试分析，构建了输出角度-输入扭矩、输入角度-输出扭矩等不同形式的刚度表达式，分析了系统刚度的非线性特性和刚度回差现象。另外，PREISSNER 等还着重研究了谐波传动模型的发展历程，建立了将非线性摩擦与刚度、迟滞回差等多影响因素考虑在内的高精度的谐波传动模型，助推了谐波减速器的建模技术发展。

对串联型工业机器人而言，其传动机构整机刚度较低，运动过程中的受迫振动是机械结构动态特性的重要考虑指标。谐波减速器作为工业机器人驱动关节的核心机械构件单元，通常会在结构设计阶段对其进行力学仿真分析，比如有限元分析等。根据模态参数进行结构优化，以避免系统出现受迫振动。然而，受零件制造误差、装配误差等多方面的影响，实际的动力学特性通常与理论设计有较大区别。因此，本文设计谐波减速器扭转实验模态的辨识方案，可实现基于运动自激励的减速器实验模态参数辨识。

1 谐波减速器扭转模态辨识方法

1.1 实验系统设计

模态参数辨识方法一般包括基于输出响应的模态参数辨识和基于输入-输出信号的模态参数辨识。辨识方法通过控制伺服电机，驱使构件按稳态正弦扫频激励信号规律运动，实现构件的运动自激励，触发构件的扭转振动，最后对模态数据进行实时采集与后处理，完成对构件模态参数的辨识。

如图1 所示为测控系统硬件环境，待测谐波减速器两端对称分布的输入角度编码器和输出角度编码器能分别提供输入、输出角度信号，为通过基于输入-输出信号的模态参数辨识提供可能，本论文重点对基于输入-输出信号的模态辨识方法进行分析。

图1 测控系统硬件环境

基于输入-输出信号的模态参数辨识方法，首先需要获取描述系统内在特性的频响函数，频响函数的分母可以计算出系统的极点，从而估计出系统的固有频率和阻尼比，频响函数的分子可以计算出系统的零点，从而估计出系统的振型。因此，实验频响函数的准确计算是实验模态分析的基础与关键。

1.2 实验频响函数的计算

在单输入输出（Single Input Single Outpt,SISO）系统中,假设x(t)、u(t)分别为系统的输入和输出信号，X(f)、U(f)分别为其对应的频谱函数，则系统的频响函数H(f)：

为方便计算，一般采取对频响函数X(f)进行离散化处理的方式：

但在实际计算过程中，该方法可能存在无意义的情况（分母为0）。为避免出现上述问题，实际过程中可以通过x(t)的自功率谱函数Sxx(f)与x(t)相对输出的互功率谱函数Sxu(f)来计算频响函数H(f)：

其中，X*(f)为X(f)的共轭函数。

通过傅里叶变换对输入信号xt(t=1,2,3,…N-1,N)的自相关函数进行处理，计算得到信号的自功率谱：

其中，N为离散信号的时间序列长度，r为当前时刻标记，k为时移，Rxx(r)表示输入信号xt的自相关函数，j表示虚数。

同样，通过傅里叶变换对输入信号xt(t=1,2,3,…N-1,N)关于输出信号ut(t=1,2,3,…N-1,N)的互相关函数进行处理，计算得到信号的互功率谱：

其中，Rxu(r)表示输入信号xt关于输出信号ut的互相关函数。

根据式（4）和（5）可得，首先需要计算信号在时域范围内的自相关函数和互相关函数，然后才能得到其自功率谱与互功率谱函数。此过程通常需要利用卷积来计算，计算量比较耗时，一般可采用韦尔奇（Welch）方法进行近似计算，可简化计算过程。

根据韦尔奇（Welch）方法，系统的自功率谱密度函数为：

其中，M为平均近似计算次数；NFFT为快速傅里叶变换过程近似计算点数；Xi(k)为输入信号x(t) 在傅里叶变换过程中的第i个数据段函数；Xi(k)和Xi*(k)互为共轭函数。

同理，根据韦尔奇（Welch）方法，系统互功率谱密度函数为：

其中，Ui(k)为输出信号u(t) 在傅里叶变换过程中第i个数据段函数；Ui*(k)和Ui(k)互为共轭函数。

最后，将式（6）和（7）带入式（3），即可求出系统的频响函数H(f)。

1.3 模态参数辨识方案设计

本文设计如图1 所示的谐波减速器测控系统基本硬件架构，基于本架构设计如图2 所示实验方案和图3 所示的模态辨识流程，最后完成对谐波减速器扭转模态参数的估计和辨识。

图2 谐波减速器模态参数实验方案

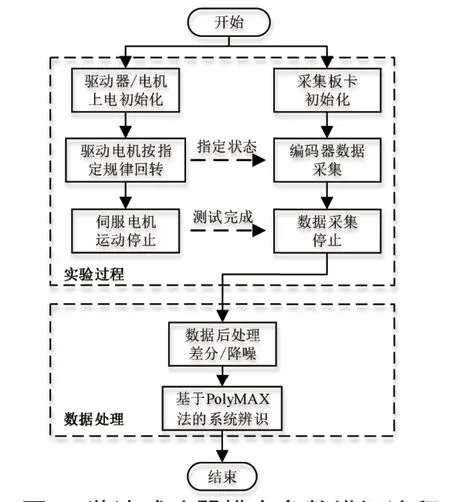
图3 谐波减速器模态参数辨识流程

如图2 和图3 所示，在谐波减速器模态实验过程中，选用稳态正弦扫频激励信号作为输入信号，通过编写满足稳态正弦扫频激励信号变化规律的程序来实现伺服电机的运行速度控制，从而实现对谐波减速器运动自激励。基于时间同步原理，可以实现输入端编码器和输出端编码器信号的同步采集，然后将输入、输出编码器信号做差分处理，可以得到系统的输入速度和输出速度，经中值滤波和小波降噪处理后作为系统的输入信号x(t) 和输出信号u(t),并由此可计算所得实验过程谐波减速器的频响函数。最后，基于实验频响函数，采用PolyMAX 模型对谐波减速器进行扭转模态参数的辨识和估计，为减速器传动性能提升奠定基础。

2 基于运动激励的谐波减速器扭转模态辨识方法实验验证分析

2.1 系统运动激励方法

模态参数是反映减速器系统固有特性的关键指标，可以为系统的结构布局、控制器的设计等提供重要参考依据。实验模态往往基于同步采集的激励信号和响应信号，构建实验频响函数，利用频响函数在频域完成模态参数的辨识。在模态参数辨识实验中，基于传统力锤和激振源的静态非工况激励无法集成于整机测控系统，本文基于上述设计的测控系统，采用运动激励方法进行谐波减速器扭转模态参数辨识实验。

在模态辨识实验中，通过计算机控制伺服电机按稳态正弦扫频信号进行运动，以此实现减速器运动自激励，激励期间同步采集减速器输入和输出端的角度信号，对采样的离散信号剔除粗大误差后，做差分处理得到输入输出端速度。由于差分运算可能会带来高频噪声，故本文将计算得到的速度信号做小波降噪处理，实现数据的平滑处理。

2.2 实验结果与分析

在实验中，首先通过运动激励方法构建系统的输入输出信号实验频响函数，最后利用PolyMAX 方法进行分析，得到系统的稳态图，如图4(a) 所示。从稳态图中的极点趋势分布可以看出，当极点位置大于20 阶时，系统趋于稳定，同时考虑到计算量，本文选定30 作为模型的拟合阶次，从而可以得到如图4(b)所示的谐波减速器实验频响分析结果。由图4(b)的频谱图可知，本实验所用谐波减速器系统一阶固有频率为，二阶固有频率。

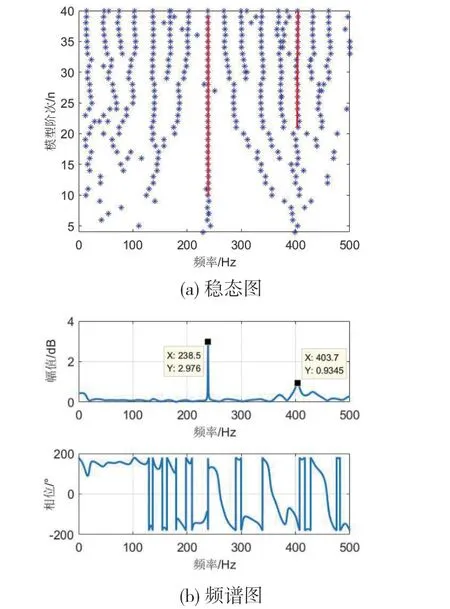
图4 基于PolyMAX 辨识方法的减速器稳态图及频谱图

为了剔除实验过程的偶然误差，在实验过程中开展多组扫频测试，最后取平均值，其实验结果如表1 所示。实验结果显示一阶固有频率的波动范围为238.4～238.6Hz，二阶固有频率的波动范围为401.6～404.1Hz，波动范围较小，一致性较高，表明了辨识结果的正确性。取各组频率值的平均值得到一阶固有频率=238.5Hz 和二阶固有频率=403.0Hz 作为PolyMAX 辨识结果。

表1 多组扭转频率辨识结果表

为了验证PolyMAX 分析方法的正确性，对采集的数据利用基于输出响应的自回归滑动平均模型（Auto-Regressive Moving Average Model，ARMA）作进一步模态辨识分析。ARMA 模型对系统输出响应信号构建线性时间序列模型，利用该时序模型实现模态参数的辨识，可广泛应用于输入激励信号难以获取或输入激励信号复杂的工程系统。

图5 所示为谐波减速器的输出响应信号稳态图，利用ARMA 分析方法，得到系统的稳态图。由于ARMA 模型只对输出响应进行分析，其分析结果包含了从系统输入到响应信号之间的所有传动链的模态参数特性，故在稳态图中应出现除了谐波减速器固有频率之外的频率成分。ARMA模型结果中在PolyMAX 分析结果固有频率附近存在频率，表明谐波减速器的固有频率在这两个频率点成为影响系统的主要频率成分。两种分析方法的对比结果如表2 所示，两种方法的一、二阶固有频率具有较高的一致性，二者相互佐证，验证了谐波减速器基于PolyMAX模态分析方法的正确性。

表2 不同辨识方法结果对比表

图5 基于ARMA 辨识方法的减速器稳态图

3 结论

谐波减速器是工业机器人驱动模块的关键部件，作为转动传动部件，谐波减速器的扭转动态特性对工业机器人的性能影响显著。本文设计了谐波减速器特性实验台，在此基础上设计了运动激励方法，通过运动激励实现了谐波减速器的扭转特性的激励；并基于PolyMax 算法，对谐波减速器的激励与输出信号进行分析，获得了准确的谐波减速器固有频率特征，为深入研究谐波减速器动态特性测试方法提供了基础。