基于模糊算法的AGV 纠偏控制

吴灏 王淇锋 刘明立 李炀 张孟珍

（1 国网石家庄供电公司,石家庄,050000；2 河北工业大学机械工程学院，天津，300401）

0 引言

目前，自动导引车（AGV）已被广泛使用在各种工业领域中，包括仓储业、制造业、危险场所和特种行业等[1-3]。在诸多应用领域中，AGV 的纠偏控制是实现自动导引控制的基础，也是AGV 研究的核心问题。AGV 纠偏控制属于离散型控制，具有非线性、模型与环境的不确定性以及测量的不精确性等特性，因其特殊性和重要性，国内外学者对AGV 纠偏控制开展深入研究。马凯等[4]针对叉车式AGV 的结构及其具有的非完整约束的特点，基于模糊控制理论实现了AGV 的路径跟踪。施文等[5]基于免疫算法的P（比例）模糊控制实现了AGV 的路径纠偏。马平等[6]采用分段模糊PI（比例-积分）控制实现了AGV 的纠偏。陈一凡[7]利用模糊控制与李雅普诺夫第二法相结合实现了AGV 的轨迹跟踪。袁鹏等[8]利用改进的粒子群优化寻求最优路径与改进模糊PID（比例-积分-微分）控制实现了AGV 的纠偏。翟宏旭[9]基于模糊控制设计了一种双输入双输出的模糊纠偏控制器，实现了AGV 的纠偏控制。孙超等[10]基于模糊控制实现了四轮驱动AGV的协同纠偏控制。

本文以AGV 为研究对象，针对AGV 在高速运行时受离散时间的影响而导致控制效果变差的问题，设计了一种模糊纠偏控制器，并基于变论域方法，对模糊纠偏控制器中输出论域进行实时变化，以提高纠偏控制在AGV 高速运行时的有效性和快速性，实现了快速、平稳地位姿纠偏。

1 AGV 运动学模型

本文研究的AGV 为四轮式结构，其中，主动轮为对角布置的舵轮，驱动策略为前舵轮驱动并控制方向，后舵轮仅驱动。

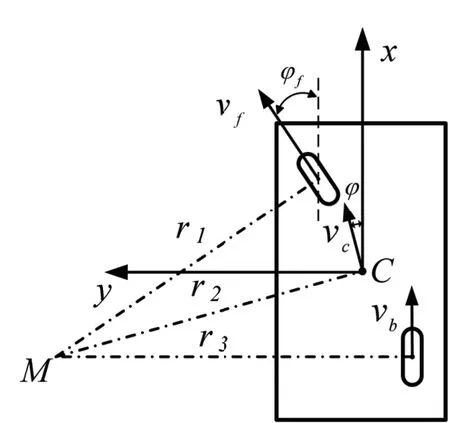
图1 AGV 左转示意图

忽略地面摩擦的影响，AGV 向左右转时的转动半径与车体的转向角，可根据几何关系与得出：

其中，L为前轮连线中点与后轮连线中点的长度，W为前轮或后轮连线的长度。

如图2 所示，以AGV 右转为例进行分析，AGV 在二维平面运动，建立基准坐标系X-O-Y。定义以车体正中心C点为AGV 的车体运动中心，并以C点为原点建立x-C-y为AGV 局部坐标系。车体的姿态角为X 轴正方向与x 轴正方向的夹角。

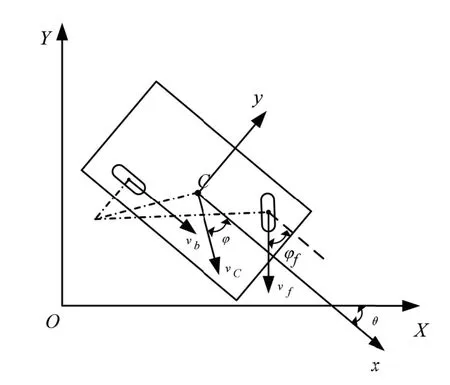
图2 AGV 右转示意图

定义AGV 顺时针旋转为负，逆时针旋转为正，则AGV 匀速行驶时的角速度为：

AGV 的运行状态可表示为：

由于AGV 的实际控制为离散控制，因此进一步离散化，得到（k+1）时刻AGV 的位姿：

2 AGV 纠偏控制器设计

如图3 所示，AGV 纠偏控制器可以通过理想位姿与AGV 的实际位姿计算出车体当前偏离轨迹的位置偏差与车体的角度偏差，通过速度进行分级推理出论域伸缩因子，进而根据AGV 的位姿偏差推理出AGV 的转向角，AGV 纠偏控制器根据车体转向角及速度调整AGV 的舵轮速度与转角，使其能够以较高的速度和精度回到原始路径上。

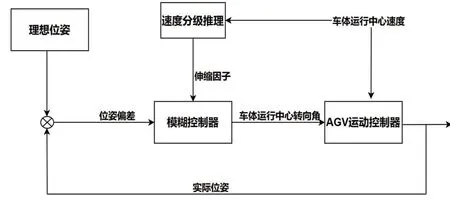
图3 纠偏控制示意图

3 变论域模糊控制

3.1 基于速度分级的AGV 控制策略

AGV 的纠偏控制是由位置偏差与车体角度偏差进行模糊推理实现，未考虑偏差变化量的影响。考虑到离散时间的影响，当AGV 高速运行时，由于缺少模糊规则，其控制效果变差。在单一的模糊控制中，模糊控制器的论域是固定的，故本文引入变论域理论[12]，设计出一种基于速度分级的AGV 纠偏控制器。

在基于速度分级的AGV 纠偏控制中，当AGV 的速度较大时，可通过调整AGV 车体运行中心转向角的输出论域（即调整模糊控制器的伸缩因子），以降低离散时间对AGV 纠偏控制的影响。

基于AGV 的运行速度分级，实现AGV 纠偏控制的整个流程如图4 所示。

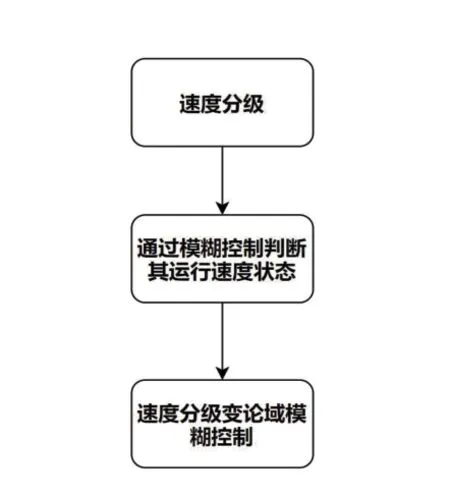
图4 分级控制流程图

3.2 变论域模糊控制原理

自适应变论域模糊控制是相对于常规模糊控制的固定论域而言的。固定的论域会使得模糊控制的适应性受到一定限制，如果初始论域范围设定过小，则导致控制结果的精度下降；如果初始论域设定范围过大，则会导致控制的稳定性下降。而变论域则是通过引入伸缩因子来调整模糊控制器输入/输出变量的论域范围。变论域原理如图5 所示，论域在伸缩因子的影响下，由初始论域

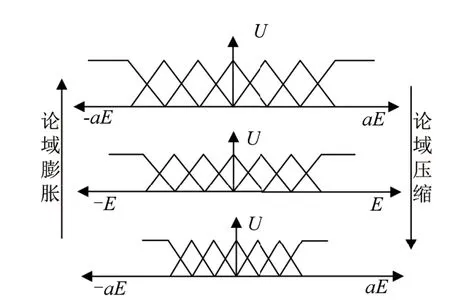
图5 变论域原理图

3.3 速度分级伸缩因子模糊控制器设计

表1 伸缩因子模糊控制器模糊规则表

车体运行中心转向角的论域的伸缩因子系数的大小通过AGV 的运行速度进行分级判定，故输出论域会随速度的大小而变化。当AGV 运行速度较低时，离散时间对于纠偏控制的影响较低，采用初始论域的模糊纠偏控制便可实现有效的纠偏；当AGV 运行速度较大时，可通过降低输出论域伸缩因子来提高其纠偏性能。

3.4 基于速度分级的AGV 纠偏控制器

本文以AGV 位置偏差大小和角度偏差大小为参量，建立模糊规则，根据车体的转向角度对位姿的影响情况，制定模糊规则表，具体如表2 所示。

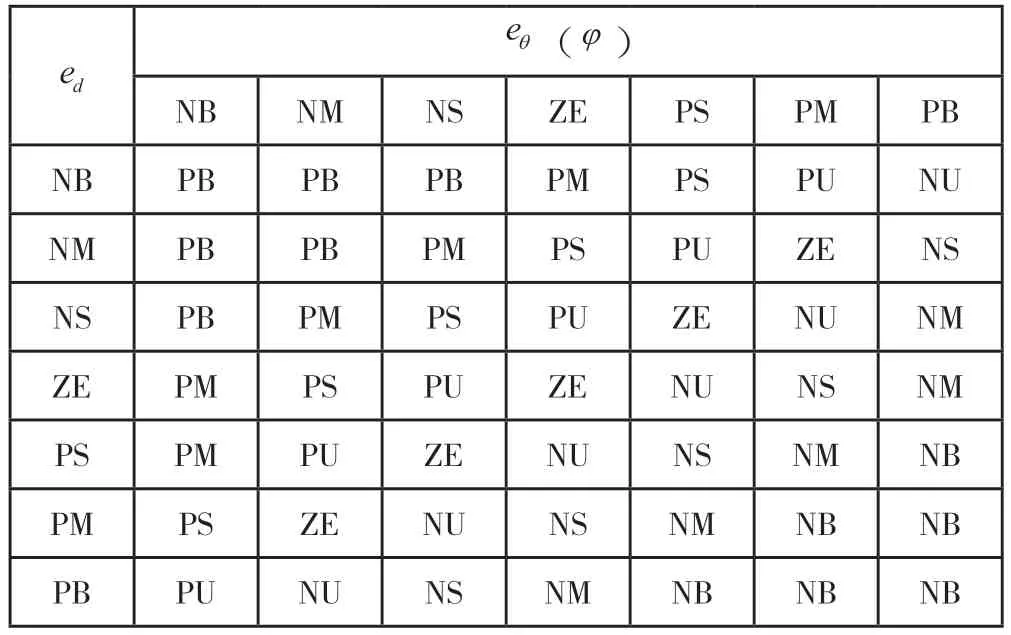
表2 模糊纠偏控制器模糊规则表

4 仿真与分析

为了验证基于速度分级的变论域模糊控制器的有效性，本文在MATLAB 软件的Simulink 平台中搭建了一套AGV 纠偏控制系统，首先对基于速度分级的变论域模糊控制器的控制效果进行仿真分析，然后与传统的模糊控制及传统的PID 控制在不同运行速度时的控制效果作对比。

设置AGV 的初始值（见表3），并进行仿真分析，分别得到AGV 位置偏差变化与AGV 角度偏差变化的仿真曲线，具体如图7、图8 所示。

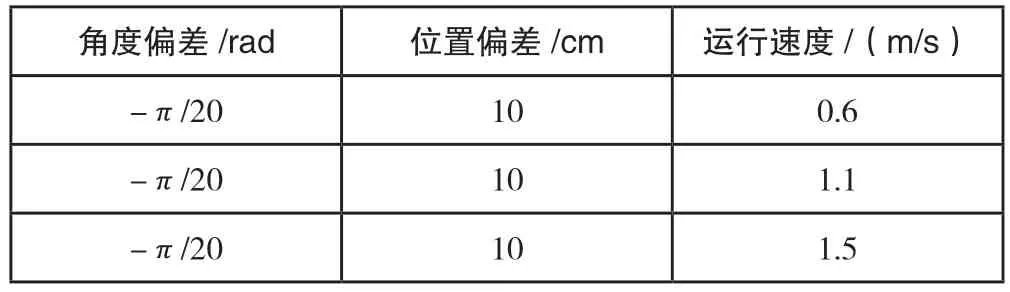
表3 AGV 初始设定值

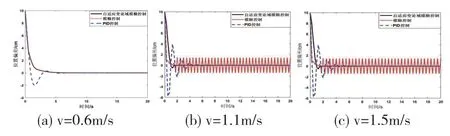
图7 AGV 位置偏差变化曲线

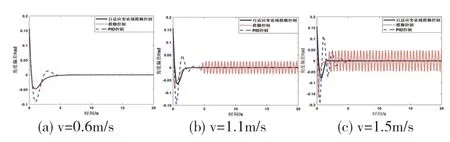
图8 AGV 角度偏差变化曲线

由图7 和图8 可知，与传统PID 控制相比，基于速度分级的AGV 纠偏控制器在不同运行速度下的纠偏性能具有更加出色的表现，且超调量远低于传统PID。在AGV 非高速运行时，基于速度分级的AGV 纠偏控制器与传统的模糊控制器具有相同的控制效果，且性能优于传统PID，能够实现AGV 的快速纠偏。

当AGV 高速运行时，基于速度分级的AGV 纠偏控制器相对于传统模糊控制器具有更好的控制效果，可以很大程度上降低系统离散时间的影响，达到更好的纠偏控制效果，同时验证了基于速度分级的AGV 纠偏控制器的有效性。

5 结束语

本文以AGV 为研究对象，根据其结构及运动特点，对纠偏控制中的模糊控制器进行设计及改进。提出了基于速度分级的理论，即以速度为输入变量，转向角模糊控制器的输出论域的伸缩因子为输出变量，设计输出论域伸缩因子模糊控制器。在多种运行速度下进行的纠偏仿真验证了基于速度分级的变论域模糊控制器的有效性，实现了AGV 快速、平稳的纠偏。