基于HJI理论的移动机器人神经网络自适应控制

刘 鑫,陈昌忠,罗 淇,孙增诚

(四川轻化工大学自动化与信息工程学院,四川 自贡 643000)

1 引言

移动机器人具有灵活性高,生产效率高,实用性强等优点,已广泛应用于工业领域和社会场所。但是,由于其具有强耦合、摩擦负载不确定等非线性特点,对于它的控制研究一直受到国内外学者的关注。文献[1,2]采用智能PID控制算法对一般PID控制算法的参数不易整定,鲁棒性差等问题进行了优化。文献[3]设计出一种新型滑模控制算法,解决了移动机器人在极坐标系中的跟踪控制问题。文献[4]针对参数不确定的运动学模型,利用反演设计了自适应控制器,并将其推广到了动力学模型中。随着控制理论的发展,神经网络技术也广泛应用于移动机器人的控制之中。文献[5]利用神经网络在线调整运动学控制器参数和补偿动力学PID控制器。文献[6]设计了一种自适应神经滑模控制器,实现了不确定动力学模型的移动机器人的轨迹跟踪控制。文献[7]利用神经网络对打滑条件下的动力学模型进行补偿,实现了打滑条件下移动机器人的轨迹跟踪。

文献[1-3]虽然具有良好的运动学跟踪效果但是并未考虑移动机器人的动力学模型。文献[4]虽然考虑了动力学模型,但是并未考虑模型不确定性和外部扰动,在实际的控制中可能出现较大的误差。

本文充分考虑移动机器人运动学模型和动力学模型的不确定建模项及不确定外部干扰等问题,设计了基于反步法的运动学控制器,利用RBF神经网络对动力学模型不确定项和外界干扰进行补偿,结合HJI理论设计了动力学控制器。利用MATLAB对本文所设计的控制方法进行数值仿真,仿真结果表明了本文设计的控制系统具有良好的鲁棒性。

2 HJI理论

在模有界条件下,非线性不确定奇异系统的鲁棒可镇定性与一个扩展的HJI微分不等式存在正解等价[8]。本文基于HJI不等式设计动力学反馈控制器,并利用HJI理论来验证移动机器人动力学系统的稳定性。

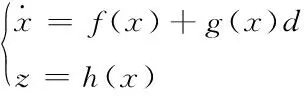
(1)

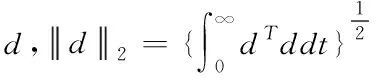
为了评判系统的鲁棒性,定义如下性能指标

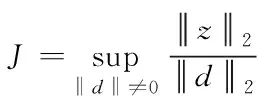
(2)

式(2)中,J为系统的L2增益,它的大小可用来反应系统鲁棒性能的好坏。J越小,系统的鲁棒性能越好。

根据文献[10],HJI理论可描述为:对任意给定一个正数γ,如果存在一个正定且可微的函数L(x)≥0,并且满足

则J≤γ。

3 移动机器人的运动学与动力学模型

考虑一类受非完整约束的差速驱动的移动机器人,其后方两侧为驱动轮,前方两侧为自由轮,自由轮仅起支撑作用,如图1所示。设两驱动轮的半径都为r,轴距为2b,点N为两轮的轴心。向量q=[xc,yc,θc]T表示移动机器人的轴心N在笛卡尔坐标系中的位置,θc表示移动机器人的运动方向与笛卡尔坐标系横轴正方向的夹角。

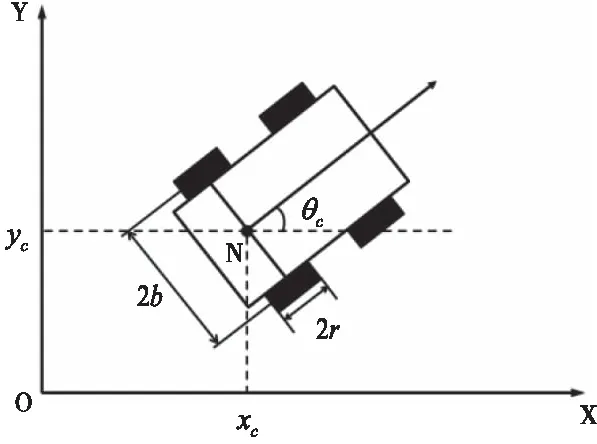
图1 移动机器人示意图

对于图1所示的移动机器人,满足纯滚动、无滑动情况下的非完整约束条件为

(3)

将(3)式改写成如下形式,即

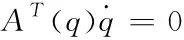
(4)

其中

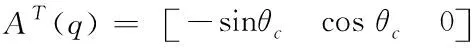
(5)

(6)

选择一个满秩矩阵S(q)为AT(q)零空间的一组基,即

ST(q)A(q)=0

(7)

存在一个辅助速度控制向量V(t),使

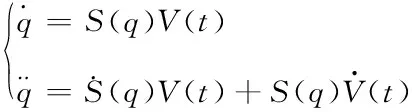
(8)

其中

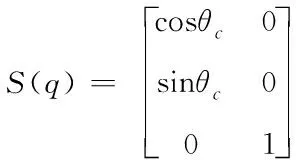
(9)

V(t)=[vω]T

(10)

v和ω分别表示移动机器人的线速度和角速度。

则非完整移动机器人的运动学方程表示为

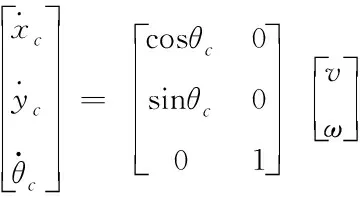
(11)

一般情况下,非完整移动机器人的动力学方程可以表示为[11]

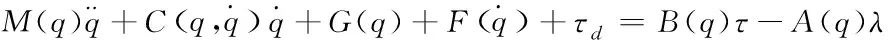
(12)

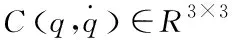
由Euler—Lagrange方程可知,移动机器人动力学模型的参数[6]

(13)

式(13)中,m表示移动机器人的质量,I表示转动惯量,τr表示其右轮力矩,τl表示其左轮力矩。

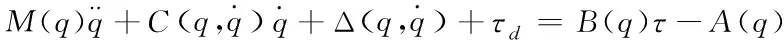
(14)

将式(14)等式左右两边分别左乘ST(q),将式(8)代入整理后得移动机器人一阶动力学模型

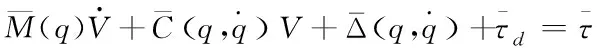
(15)

其中

由文献[12]可知式(15)具有以下性质

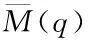
结合式(7)、式(11)和式(14)可得

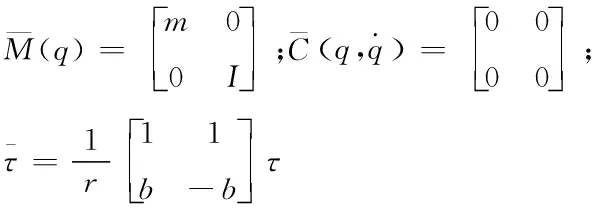
(16)

4 控制器设计

为了实现移动机器人位置跟踪,本文针对移动机器人运动学模型和动力学模型分别设计相应的控制器,具体如下:

1) 针对移动机器人的运动学模型采用反步法设计辅助速度控制率。

2)针对移动机器人的动力学模型,基于HJI理论设计具有RBF神经网络补偿模型不确定项和外部干扰的动力学控制器。

4.1 运动学控制器设计

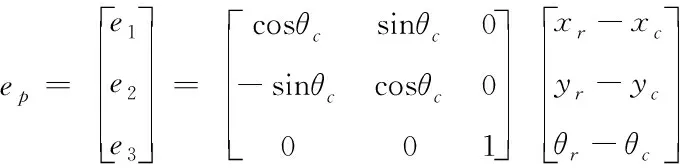
(17)

对位置跟踪误差求导,可得误差变化率

(18)

在给定参考线速度vr≥0,角速度ωr≥0的基础上采用反步法设计运动学控制器[13]

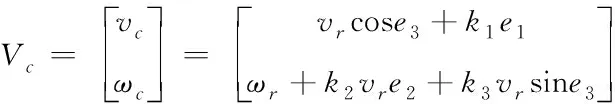
(19)

其中,k1,k2,k3为大于0的可调节参数。

4.2 动力学控制器设计

RBF神经网络能在一个紧凑集和任意精度下逼近任何非线性函数[14]。本文利用RBF神经网络对移动机器人的动力学模型存在不确定建模项和不确定外部扰动进行逼近。

设

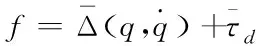
(20)

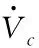
f=W*σ+εf

(21)

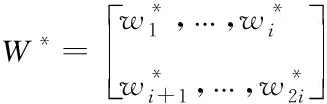
由于存在逼近误差,利用自适应算法调节神经网络的权值,则神经网络的估计输出如下

=σ

(22)

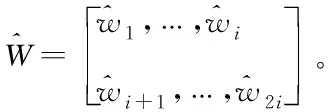
定义速度跟踪误差为

ec=V-Vc

(23)

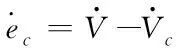
(24)

设计如下自适应率

=-ηecσT

(25)

其中,η为大于0的可调节参数。

结合式(15),式(20)和式(21)可得RBF神经网络逼近下的动力学模型为

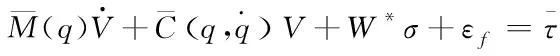
(26)

根据该模型,设计前馈控制率为

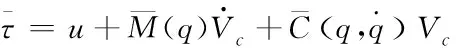
(27)

其中,u为反馈控制率。

将式(27)代入式(26)整理后得

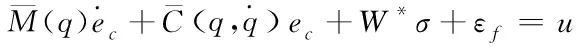
(28)

将速度跟踪误差ec作为评判指标z,则

z=ec

(29)

式(28)可改写成

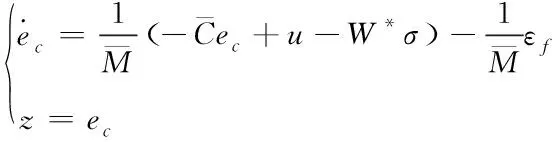
(30)

式(30)中,设

h(ec)=ec

则式(30)可该写成式(1)的形式。

为了保证动力学系统误差收敛,根据HJI理论设计反馈控制率为

(31)

5 系统稳定性分析

定义运动学系统和动力学系统的Lyapunov函数分别为L1和L2

(32)

(33)

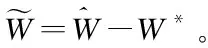
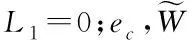
对式(32)求导可得

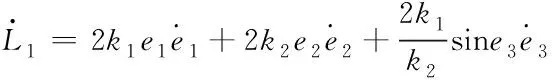
(34)

结合式(17),(18),(19)可得

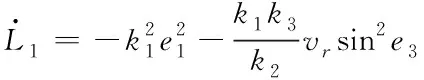
(35)

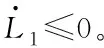
对式(33)求导可得

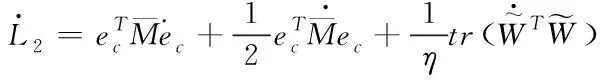
(36)

结合式(28),式(36)可以改写为

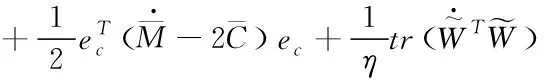
(37)

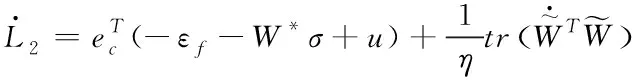
(38)

将反馈控制率式(31)代入式(38)中,可得

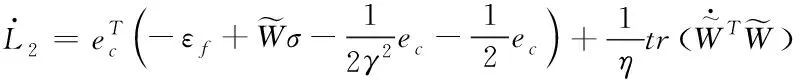
(39)

定义

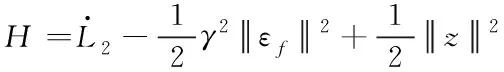
(40)

将式(39)代入上式,整理可得

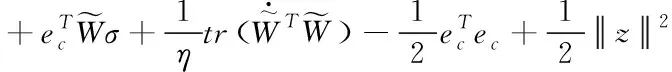
(41)

由于

可知H≤0,则

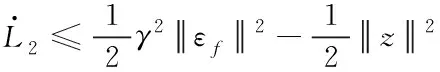
(42)

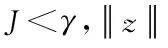
根据以上分析验证,设计移动机器人的控制系统结构如图2所示。

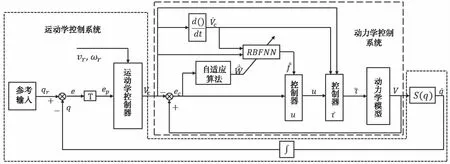
图2 基于HJI理论的轮式移动机器人的神经网络控制

6 仿真结果及分析

图3为移动机器人圆轨迹跟踪仿真曲线,图4为圆轨迹跟踪下移动机器人的位置跟踪误差。由图3和图4可以看出,移动机器人能够快速,平稳,且准确的跟踪上参考轨迹。且位置跟踪误差快速收敛到0,几乎无抖动,表明控制系统具有良好的鲁棒性。

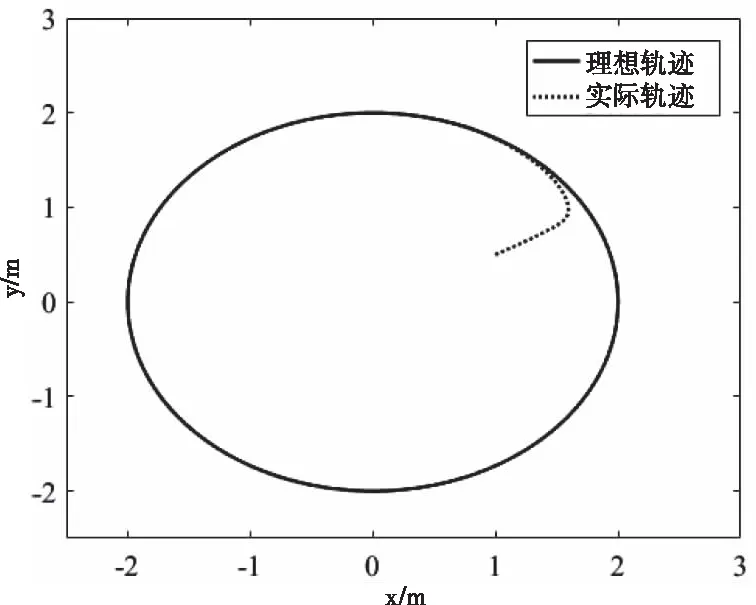
图3 轨迹跟踪曲线

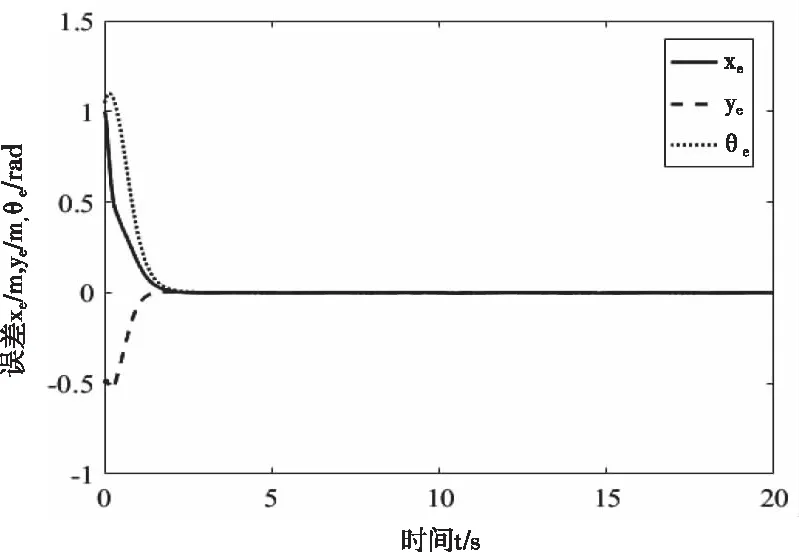
图4 位置跟踪误差曲线

图5为动力学控制器对辅助速度控制输入的跟踪曲线。由图可知,速度控制输入平稳无跳动,且实际速度能够很快且准确的跟踪上辅助速度控制输入,说明本文所设计的动力学控制器具有良好的跟踪性能。

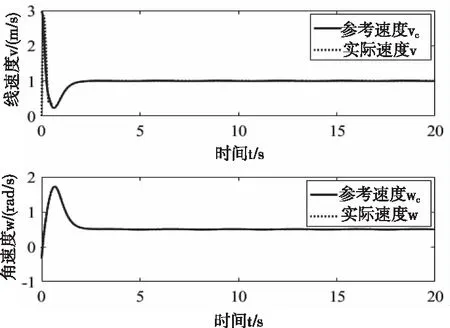
图5 辅助速度跟踪曲线

图6为移动机器人左右轮的控制力矩输入曲线。由图可知,左右轮的控制力矩呈正余弦波动,这是由于力矩控制器中存在RBF神经网络的补偿控制,而RBF神经网络是对不确定项的逼近,这样力矩控制器恰好能抵消不确定项,提高系统的鲁棒性。

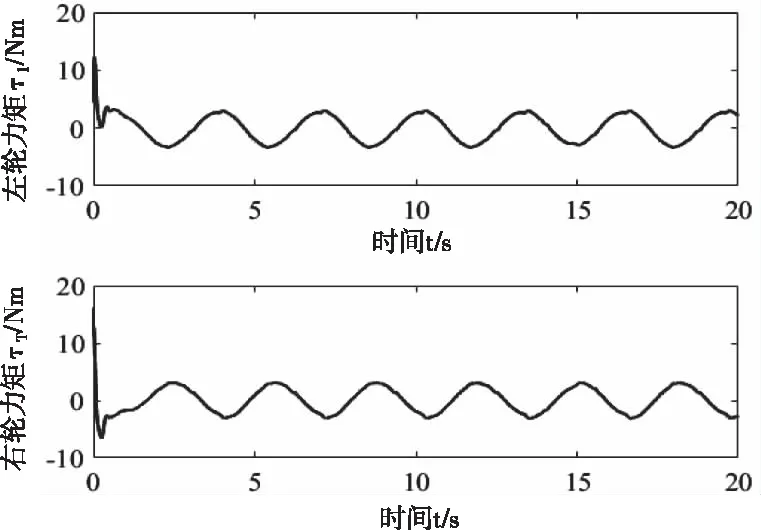
图6 驱动力矩输出曲线

图7为RBF神经网络对不确定建模项和不确定外界干扰的逼近曲线。由图可知,所设计的RBF神经网络能够快速且准确的逼近不确定项。

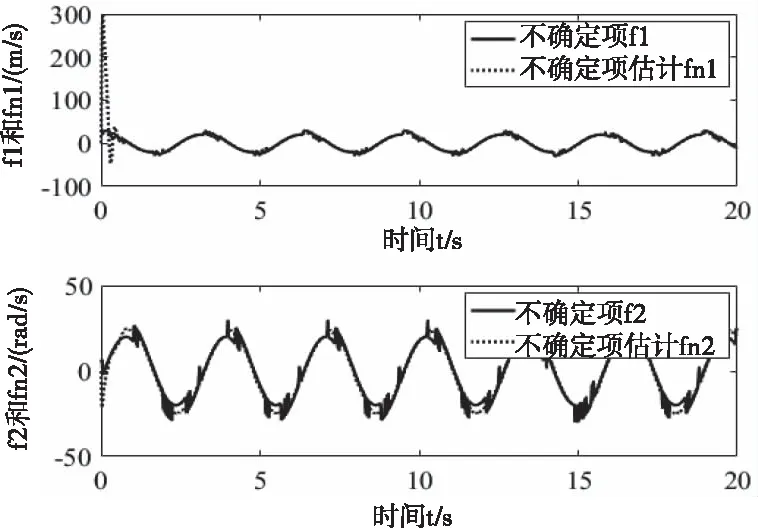
图7 不确定项逼近曲线

7 结论

本文以动力学模型具有不确定建模项和不确定外界扰动的非完整轮式移动机器人为研究对象,分析了其运动学和动力学模型,介绍了HJI理论,并在此基础上设计具有RBF神经网络补偿的移动机器人控制方法。通过MATLAB软件对移动机器人进行轨迹跟踪仿真,仿真结果表明,RBF神经网络能够快速准确地逼近不确定项,移动机器人能够快速,平稳,准确的跟踪参考轨迹。在有较大不确定建模项及外界干扰等因素的影响下,该控制方法下移动机器人依然具有良好的跟踪效果,且相对于文献[5,6],控制器需要调节的参数少。