基于FGO的GNSS/INS组合导航完好性监测算法
兰晓伟,许承东,赵 靖
(1. 北京理工大学宇航学院,北京 100081;2. 中国交通通信信息中心,北京 100011)
1 引言
完好性是导航系统四种关键服务性能(精度、连续性、完好性、可用性)之一,用于提供对导航系统所提供信息正确性的置信度的测量,也包括系统在无法用于导航时向用户发出告警[1]。完好性监测是确保导航系统满足完好性风险需求的重要手段,与导航用户的生命财产安全息息相关。现有的完好性监测技术包含故障检测和完好性风险评估两方面,前者通过构造检验统计量与检测阈值判断有无故障发生,后者提供保护级限定用户定位误差的安全边界[2]。
接收机自主完好性监测(Receiver Autonomous Integrity Monitoring,RAIM)是目前针对全球导航卫星系统(Global Navigation Satellite System,GNSS)应用最广泛的完好性监测手段。众多学者针对RAIM算法展开了广泛而深入的研究,如双星座RAIM算法[3]、模糊聚类RAIM算法[4]和高级RAIM算法(Advanced RAIM,ARAIM)[5]等。但仅依靠GNSS测量信息,难以满足完好性需求更为严苛的场景。
GNSS与惯性导航系统(Inertial Navigation System,INS)具有优势互补的特点,二者的组合能够显著改善导航精度,同时也为增强导航系统的完好性提供了可能。传统的GNSS/INS组合导航系统基于卡尔曼滤波器实现。滤波器的递推特性对于完好性监测算法的设计造成了较大困难。现有的基于滤波器实现的GNSS/INS完好性监测算法大多只考虑故障检测,虽提高了对于卫星故障的检测效果,但忽略了保护级的计算[6],[7]。
近年来,因子图优化(Factor Graph Optimization,FGO)作为一种新型导航估计算法逐渐受到关注。研究表明,相较于扩展卡尔曼滤波器,FGO使得GNSS/INS组合导航系统能够获得更高的导航精度[8]。此外,FGO将GNSS/INS组合导航的非线性数据融合问题转化为非线性最小二乘问题,其求解过程本质为线性最小二乘的多次迭代,该特点也为故障检测和保护级计算提供了便利。
因此,本文通过引入因子图优化将GNSS/INS组合导航的非线性数据融合问题转化为迭代的线性最小二乘问题,并基于最小二乘残差构建检验统计量实现故障检测,通过定义斜率寻找最坏故障情况计算保护级,实现完整的GNSS/INS组合导航完好性监测。最后通过动态仿真数据对所提算法的有效性进行了验证。
2 因子图优化GNSS/INS组合导航算法
本文采用的GNSS/INS组合导航框架[8]如图1所示。基本的解算流程为:首先姿态航向参考系统结合地磁强度和角速度信息解算得到载体的姿态矩阵;其次通过姿态矩阵将本体坐标系的加速度转换至导航坐标系,并通过积分器获得导航坐标系下载体的速度增量;最后结合载体的速度增量以及所有可见卫星的伪距和伪距率测量值构建因子图优化模型进行导航解算,获得当前时刻载体位置、速度估计值。

图1 GNSS/INS组合导航解算框架[8]
2.1 GNSS/INS组合导航因子图模型
图1使用的因子图模型如图2所示。图中的圆圈表示变量节点,代表某时刻需要估计的状态变量;黑色方框表示因子节点,代表对于状态变量的观测。
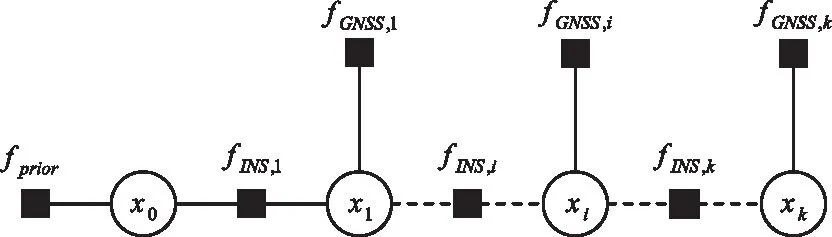
图2 GNSS/INS组合导航因子图模型

图3 组合导航完好性监测算法仿真流程
在因子图优化中,所有传感器的测量均以因子函数fj表示。将与因子函数fj相关联的状态变量记为xj,基于因子图优化的组合导航解算过程实际上为求解如下的最大后验估计问题
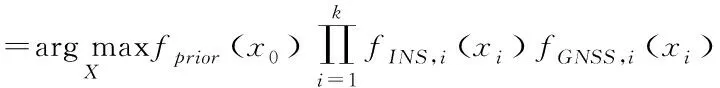
(1)
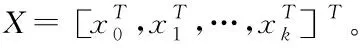
当所有传感器的测量噪声均为高斯白噪声时,各因子函数具有如下形式:
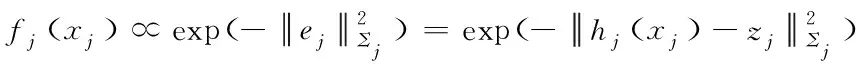
(2)

2.2 各类因子及其观测函数
2.2.1 先验因子
在GNSS/INS组合导航中,先验信息通常为初始状态的估计值,其观测函数和观测值分别为
(3)

2.2.2 INS因子
在GNSS/INS组合导航因子图中,INS因子描述了前后两个时刻状态变量之间的关联。其对应的观测值和观测函数为
(4)
本文中,导航坐标系选取为东北天(ENU)坐标系,状态变量选取为8维向量,其构成为
(5)
式中,pk=[ek,nk,uk]T表示载体在ENU系下的位置,vk=[ve,k,vn,k,vu,k]T表示载体在ENU系下的速度,δtk表示接收机钟差,δfk表示接收机频漂。
式(5)中的F为状态转移矩阵,B为控制矩阵,其元素构成分别为

(6)
式中,I为单位矩阵,ΔT为计算周期,τf为频漂对应的时间常数。
式(5)中的δvk为一个计算周期内根据加速度计测量值积分得到的速度增量,假设ΔT内共有m个加速度计采样值,则δvk的表达式为

(7)

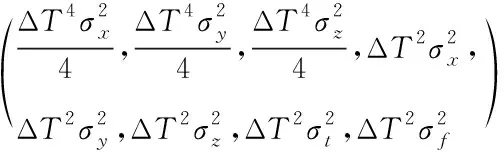
(8)
2.2.3 GNSS因子
本文中采用的GNSS观测量为伪距和伪距率,假设k时刻共有lk颗可见卫星,则GNSS因子对应的测量值zk,GNSS为

(9)
伪距观测量对应的观测函数为

(10)
伪距率观测值对应的观测函数为

(11)
进而,GNSS因子对应的观测函数为
hk,GNSS(xk)=[hρ,1,…,hρ,lk,hρ,1,…,hρ,lk]T+εk,GNSS
(12)
GNSS因子对应的误差方差阵Σk,GNSS为

(13)
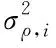
2.3 因子图优化
通过对式(1)右侧各项取负对数可将式(1)所描述的最大后验估计问题转换为非线性最小二乘问题,即
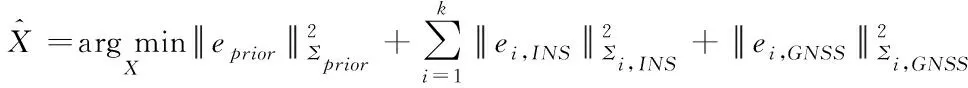
(14)
通过一阶泰勒展开可将上式进一步转化为线性最小二乘问题
δ
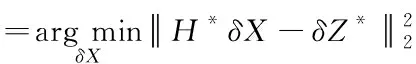
(15)
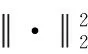
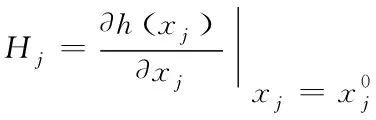
(16)
式(15)的解为
δ=H*TδZ*
(17)

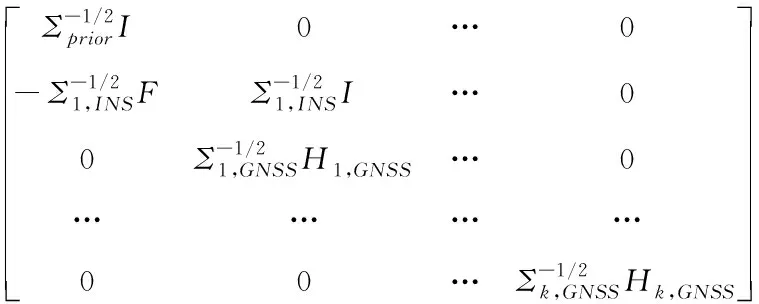
(18)
通过高斯-牛顿法多次迭代可获得式(14)的优化解
X0=X0+δ
(19)
当δ足够小时,认为迭代过程已经收敛,可将此时的X0视作式(14)的解。
3 完好性监测
通过第2节所描述的因子图优化算法将GNSS/INS组合导航问题转化为线性最小二乘问题。本节将在线性最小二乘的基础上进行故障检测和保护级计算。
3.1 故障检测
将最后一次迭代所对应的式(15)转换为如下形式
δZ*=H*δX+ε*+b*
(20)
式中,ε*~N(0,I)为归一化后的测量误差,b*为归一化后的故障向量


(21)
最小二乘残差定义为
r=δZ*-H*δ=(I-H*S)(ε*+b*)
(22)
最小二乘残差平方和的统计特性为
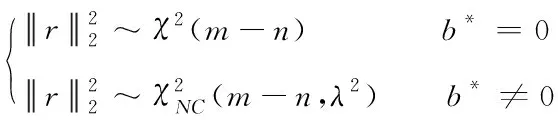
(23)
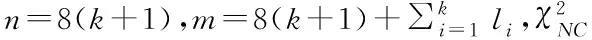
λ2=b*T(I-H*S)b*
(24)
根据连续性风险需求Creq以及式(23)描述的统计特性可确定故障检测门限值TFGO
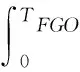
(25)

3.2 保护级计算
保护级用于评估故障检测算法的完好性风险。以垂向为例,垂向完好性风险PI,v定义为
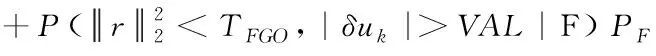
(26)
式中,δuk为当前时刻垂向定位误差,VAL为给定的垂向告警门限;NF为无故障模式,PNF=(1-Psat)N为无故障模式先验概率,N为可见卫星数,Psat为卫星先验故障概率;F表示故障模式,PF=1-PNF为故障模式先验概率。
将式(26)等号左侧替换为垂向完好性风险需求Ireq,v,等号右侧的VAL替换为VPL即为垂向保护级的计算公式

(27)
对于式(27),一种保守的解法是将Ireq,v平均分配,分别计算无故障模式和故障模式下的保护级,并取其最大值作为最终的保护级[2],即
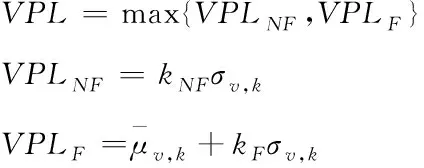
(28)
式中,σv,k为当前时刻垂向定位误差的标准差;kNF和kF分别为无故障模式和故障模式对应的系数,其表达式为
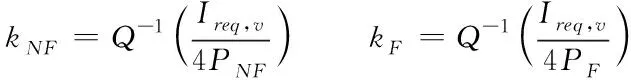
(29)
式中,Q-1为标准正态分布概率累积分布函数的逆函数。
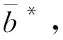

μv,k=-TXSb*
(30)
δ的估计误差方差阵为Σ=,当前时刻垂向定位误差的标准差为

(31)
在完好性监测算法中,斜率定义为未知故障引起的均值漂移与非中心化参数的比值,即
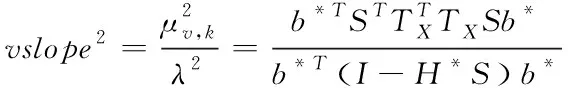
(32)



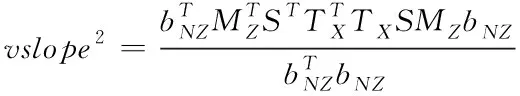
(33)

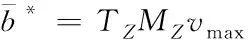
(34)
综上,垂向保护级的最终表达式

(35)
4 仿真分析
4.1 仿真条件
为验证本文提出的GNSS/INS组合导航完好性监测算法的有效性,选取载体典型运动轨迹进行仿真。仿真环节主要包括运动信息仿真,测量信息仿真和算法仿真三部分:运动信息仿真用于产生卫星位置、卫星速度以及载体理想运动轨迹;测量信息仿真用于产生卫星的伪距/伪距率模拟测量信息,载体的姿态角和比力模拟测量值以及卫星的故障信息;算法仿真部分用于实现所提组合导航算法以及完好性监测算法,并对其性能进行验证。仿真流程如图4所示。

图4 载体飞行轨迹
载体900s内的运动轨迹包括平飞、爬升、转弯等多个阶段,其飞行轨迹如图4所示。
本次仿真中GNSS星座选取为GPS,卫星伪距和伪距率误差均建模为白噪声,惯性传感器误差选取为民航飞机组合导航仿真的典型值,其具体数值见表1。加速度计的采样频率为50Hz,GPS测量值的采样频率为2Hz。

表1 GPS卫星与INS测量噪声仿真参数
仿真过程中完好性相关参数取值如表2所示

表2 完好性相关参数取值
此外考虑到随着历元数的增加,因子图优化算法需要占用的计算资源也随之增加,本文采用滑动窗口的策略避免这一问题,滑动窗口的尺寸选取为50个历元。
将本文所提算法记为因子图优化完好性监测算法(FGO-IM),下文将通过与文献[2]中基于卡尔曼滤波器实现的加权最小二乘完好性监测算法(WLS-IM)对比以展示本文所提算法的性能提升。
4.2 故障检测
当卫星PRN9在200-400s内注入大小为15m的伪距故障偏差时,FGO-IM和WLS-IM检验统计量与检测阈值的比值如图5所示。由图可知,相较于WLS-IM,所提FGO-IM算法对于同样大小的伪距故障更为敏感。在给定的故障条件下,FGO-IM的故障检测率接近100%,而WLS-IM只有在少数历元检验统计量超过了检测阈值。但是,与WLS-IM相比,由于FGO-IM利用了过去历元的测量信息,FGO-IM对于故障的响应具有一定的滞后性。

图5 PRN9伪距故障时故障检测性能
将故障检测率定义为检测到故障的历元数占故障发生历元数的百分比,则FGO-IM和WLS-IM对于发生在PRN9上的不同大小伪距故障的检测率如图6所示。FGO-IM和WLS-IM均在伪距故障约为10m时开始能够在部分历元检测到故障发生。当伪距故障达到15m以上时,FGO-IM的故障检测率已经达到100%。但是对于WLS-IM,只有当伪距故障大小超过45m时,其故障检测率才能达到100%。因此,相较于WLS-IM,所提FGO-IM较为显著地提升了对于伪距故障的检测性能。
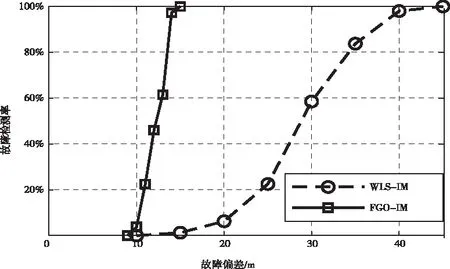
图6 两种算法伪距故障检测率对比
当卫星PRN9在200-400s内注入大小为1m/s的伪距率故障偏差时,检验统计量与检测阈值的比值如图7所示。由于WLS-IM在进行故障检测时未利用伪距率信息,因此其检验统计量对于伪距率故障无任何响应。而所提FGO-IM算法综合利用了伪距和伪距率信息,对于伪距率故障也具有较好的检测效果。在给定的伪距率故障条件下,FGO-IM算法的故障检测率接近100%。

图7 PRN9伪距率故障时故障检测性能
4.3 保护级
无故障条件下,WLS-IM和所提FGO-IM算法计算得到的垂向保护级如图8所示。整体而言,通过FGO-IM计算得到的垂向保护级保持在20m附近,相较于WLS-IM,垂向保护级明显得到降低,意味着相同条件下FGO-IM具有更高的可用性。在仿真过程中,450s后卫星PRN18不再可见,由此引起的卫星几何变化会造成垂向保护级的增大。但相较于WLS-IM,由于FGO-IM利用了过去历元的测量信息进行平滑,尽管450s后卫星几何变化同样引起其垂向保护级增大,但增大量并不显著,即对其可用性影响较小。此外,由于采用了滑动窗口算法,在初始历元和卫星几何变化的历元,FGO-IM的垂向保护级需要一定时间收敛至稳定值。
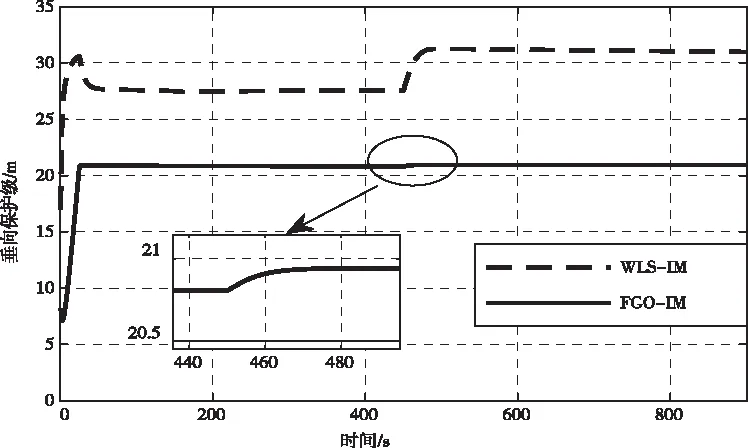
图8 无故障时垂向保护级
保护级的重要意义在于提供FGO-IM在未检测到故障时载体定位误差的安全边界。未检测到故障分为两种情况:无故障发生或发生了故障却未被检测到,即漏检情况。漏检情况对于用户而言非常危险。在200-400s向PRN11注入大小为5m的伪距故障,在500-700s向PRN16注入大小为0.4m/s的伪距率故障,用于模拟漏检情况。该条件下检验统计量与检测阈值之比如图9所示,此时某些时刻的检验统计量已经非常接近检测阈值,但由于二者之比始终低于1,未触发FGO-IM 的告警。

图9 漏检时的检验统计量与阈值之比
在模拟的漏检情况下,所提算法的垂向定位误差(VPE)与垂向保护级的变化曲线如图10所示。由图可知,即使在模拟的极限漏检情况下,垂向定位误差绝对值始终保持在FGO-IM提供的垂向保护级之下。这表明所提FGO-IM的保护级算法是有效的,能够提供未检测到故障情况下用户定位误差的安全边界。
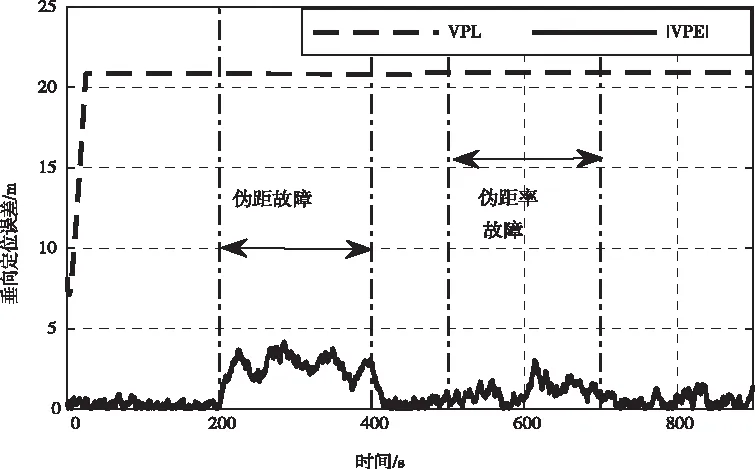
图10 漏检时的垂向定位误差与垂向保护级
5 结论
针对GNSS/INS组合导航中GNSS卫星的故障风险,本文提出一种基于因子图优化的组合导航自主完好性监测算法。在构建的GNSS/INS因子图模型基础上,将导航估计问题转化为多次迭代的线性最小二乘问题,利用最小二乘残差构建检验统计量进行故障检测和保护级计算。对动态数据的仿真结果表明,相较于传统算法,所提出的完好性监测算法能够更加有效地检测GNSS卫星的伪距和伪距率故障,且保护级在大幅降低的同时能够有效包络漏检情况下的定位误差。

