基于垂直航迹的冲突解脱模型研究

赵浩迪,朱代武,刘 豪

(中国民用航空飞行学院,四川 广汉 618300)

1 引言

随着世界经济快速发展,世界范围内民航运输需求稳步上升,航班量日益增多,民航运输提出了新的要求和挑战。空中交通管理效率的提升是空管的核心问题,为此国际民航组织提出了基于航迹运行(TBO)概念[1]。TBO技术基于导航与监视技术的稳定性与精度的提升,使得航空四维航迹的获取和推测能够满足实时管理[2]。在此之上可以做到航空器飞行航迹的自由规划,从而达到提升空域使用效率,提高航空运行安全性,降低航空运行成本的目的。

在TBO技术中,较为核心的是冲突解脱技术[3]。目前的冲突解脱主要由管制员通过雷达观察或飞行员自主位置报判定航空器之间的交通态势和潜在冲突,通过话音指令指挥航空器改变航行诸元以消除冲突。TBO技术支持下,可以做到自动空中交通管理,对航空器指定无冲突航迹。当前对冲突解脱技术的研究主要集中于水平四维航迹上的航行诸元改变以达到避撞,如基于图搜索的规划算法[4],基于采样的规划算法[5],插值曲线规划算法[6],优化算法[7]等。垂直解脱策略相对较少,Bayen最早提出以拉格朗日模型赋予航空器不同高度飞行以解决飞行冲突[8],高梦雨等人也采用着色法赋予航空器无冲突计划巡航高度[9],但是都没有考虑航空器上升下降过程中的冲突问题。其主要原因是由于两点:垂直调整产生冲突较为复杂,整体最优化冲突解脱方案不易确定;航空器在垂直移动的精度依然由气压式高度表定位,其稳定性受影响因素过多,垂直航迹不确定性过大。

基于航迹运行技术是4D航迹概念的重要组成部分,水平范围内航迹改变与调速的模型与算法发展已相对成熟,但在垂直范围内的中期冲突解脱技术却相对较少。

本文针对垂直冲突解脱,构建了新的模型,并将航空器改变的过程视为从高度改变开始到到达目标高度改平期间,在时域内同时占有从起始高度到目标高度之间所有高度层的方式,为冲突解脱提供足够安全裕度,并为后续提升效率的研究创造突破口。

2 航空器堆叠时序

空域内航空器在指定航迹下经过冲突探测后,会出现航空器不满足水平间隔的情况,我们将这种情况称为堆叠。在传统的研究中,都是先假设航空器飞行高度确定,再在同飞行高度的航空器间进行水平冲突探测,在这种冲突探测后的解脱策略下,堆叠状态是不被允许的,需要对航空器飞行航迹进行调整,以满足所有相关航空器不可处于堆叠状态。

2.1 堆叠相关性

在本文提出的TBO运行策略中,单架航空器可以在自身飞行性能允许的条件下在本区域飞行的时域内随时进行调整。在航空器探测时域内高度未知的情况下,对所有航空器进行水平航迹冲突探测,若航空器处于堆叠状态,视为可以容忍,并记录下航空器相互靠近进入堆叠状态和相互远离结束堆叠状态的时刻。将整个时域按堆叠状态改变的时刻进行分段,每段时域内航空器堆叠状态不变,即航空器在水平范围内相关性不变。

2.2 建立相关矩阵

以空域内第i架航空器为参考系,在空域内运行时域为时间轴,提取航空器加入或离开该航空器的堆叠时刻建立离散序列Tm,那么每时序点下有该航空器堆叠关系向量

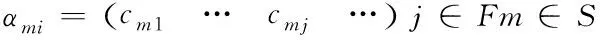
(1)

F为全时域内所有航空器集合,S为离散时刻序列集合,cmj为0/1变量,若该时刻航空器i与第j架航空器处于堆叠状态,则cmj=1;若不处于堆叠状态,则cmj=0;当i=j时,cmj=0。

由此可知在某一时刻区域内堆叠状况改变的时刻Tm下,可建立全区域堆叠相关矩阵

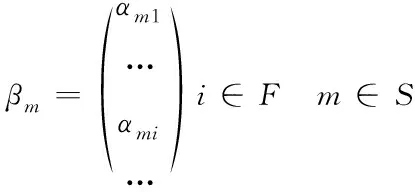
(2)

如图1所示,此时区域内共有5架航空器。

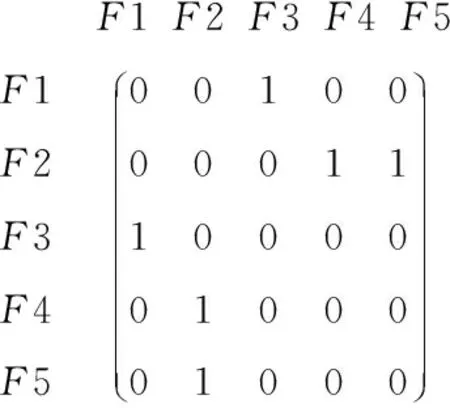
图1 对叠相关性矩阵

2.3 堆叠时刻分析

由于时序中Tm是航空器相关性改变的时刻,所以时域Tm与Tm+1之内,航空器相对关系均满足式(2)。

航空器在时域内相关状态确定,则需要为航空器在时域内分配高度,使得处于堆叠相关航空器之间飞行高度不同,以避免飞行冲突。假设Tm时刻下,航空器经高度分配均处于无冲突状态,而Tm+1时刻航空器相关性矩阵更新产生改变,有新的航空器加入堆叠(也有可能有航空器离开堆叠)带来新的冲突(或堆叠减少使得航空器有了更合理的巡航高度资源),使得Tm时刻的高度分配无法满足Tm+1的需求,故高度在Tm+1时刻需要重新分配。

航空器由一个高度层进入到下一个高度层需要爬升或下降时间,由于大气环境和航空器性能,航空器在上升下降过程中并不能严格保持稳定的上升下降率,所以此时段间内视为航空器占用了初始和目标之间所有高度层。航空器在时序间状态应连续,即航空器从Tm时刻的状态到Tm+1时刻的状态变化应满足Tm到Tm+1时隙宽度约束。航空器可能在为满足后续时刻的高度要求,Tm时刻下依然处于爬升/下降状态,故第i架航空器过Tm时刻应分配占用初始高度fsmi与目标高度femi之间所有高度层(若fsmi=femi,则航空器处于平飞)。

针对不同航空器性能,当日载重量和初始及目标高度大气环境不同,占用时间也不同,第i架航空器爬升/下降所需时间为φi(fsmi,femi),如图2所示。

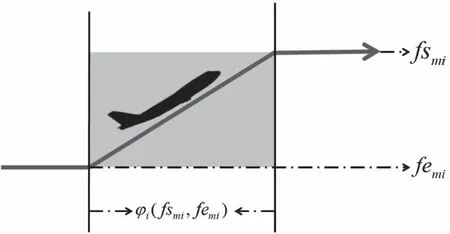
图2 时域高度层占用

并且由于航空器改变高度的需求是新的堆叠相关航空器加入或离开,故Tm到Tm+1时刻之间航空器最多需要进行一次改平,而不会频繁改变高度。

同时为建立完整约束模型,设置中间变量tmi。若Tm时刻下第i架航空器依然处于爬升/下降状态,还保持需要持续此状态tmi时间后到达目标高度,若第i架航空器平飞状态过Tm,则tmi=0。为使得tmi在任意情况下都是确定值从而简化模型约束条件的状态递推,假定航空器高度改平时机为进入下一堆叠改变时序时刻或该时隙内下一次上升开始时刻。

为将高度层与堆叠相关矩阵关联,以便之后为约束条件加入开关变量,建立航空器第i架航空器Tm时刻下身份向量

(3)

其中第i行为1,其余行均为0。

2.4 过时刻点状态

由于Tm到Tm+1时刻之间航空器最多需要进行一次改平,故Tm到Tm+1时刻之间航空器状态可以分为7种,分状态讨论Tm与Tm+1时隙宽度约束。

2.4.1 状态一:

航空器在Tm到Tm+1时刻之间保持平飞,满足

(4)

时隙内航空器侧面航迹如图3所示。

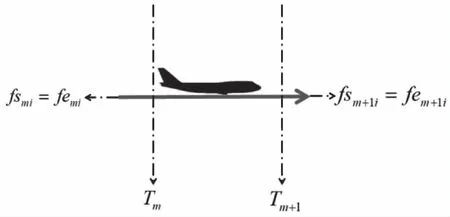
图3 保持平飞

2.4.2 状态二:

航空器在Tm时刻保持平飞,在Tm到Tm+1时刻之间开始爬升/下降高度,并在Tm+1时刻之前改平,此时

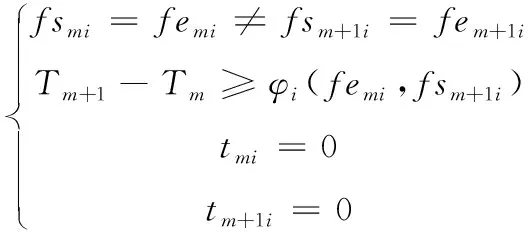
(5)

时隙内航空器侧面航迹如图4所示。

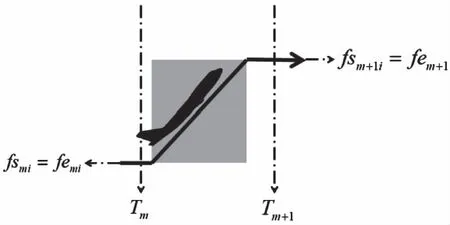
图4 平飞-上升-改平

2.4.3 状态三:

航空器在Tm时刻前开始爬升/下降,并于Tm时刻保持爬升/下降状态,在Tm+1时刻之前改平,此时

(6)

时隙内航空器侧面航迹如图5所示。

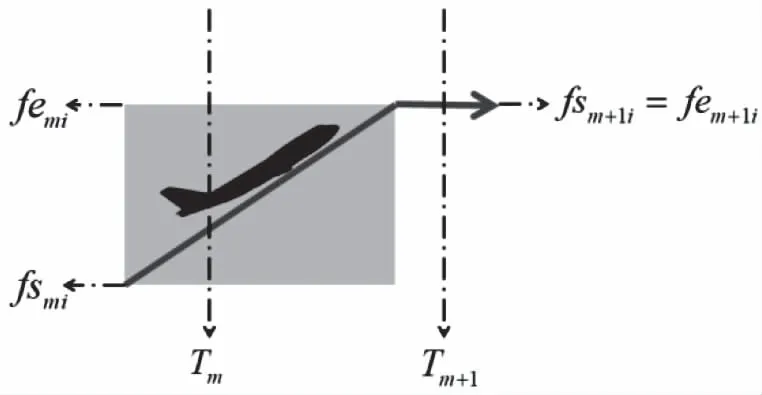
图5 上升-改平

2.4.4 状态四:

航空器于Tm到Tm+1时刻之间持续爬升/下降,于Tm与Tm+1时刻保持爬升/下降状态,此时

(7)

时隙内航空器侧面航迹如图6所示

图6 持续上升

2.4.5 状态五:

航空器在Tm时刻保持平飞,在Tm到Tm+1时刻之间开始爬升/下降高度,并在Tm+1时刻仍保持爬升/下降状态,此时

(8)

时隙内航空器侧面航迹如图7所示

图7 平飞-上升

2.4.6 状态六:

航空器在Tm时刻前爬升/下降,于Tm时刻保持爬升/下降状态,在Tm+1时刻之前改平后为满足后续潜在冲突而在Tm+1之前提前爬升/下降,并在Tm+1时刻仍保持爬升/下降状态,此时

(9)

时隙内航空器侧面航迹如图8所示

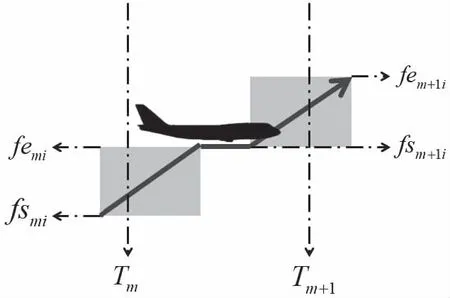
图8 上升-平飞-上升

2.4.6 状态七:

航空器在Tm时刻保持平飞,在Tm到Tm+1时刻之间开始爬升/下降高度,并在Tm+1时刻之前改平后为满足后续潜在冲突而在Tm+1之前提前爬升/下降,并在Tm+1时刻仍保持爬升/下降状态,此时

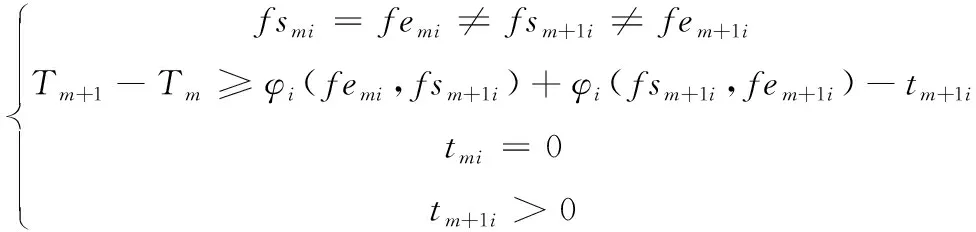
(10)

时隙内航空器侧面航迹如图9所示

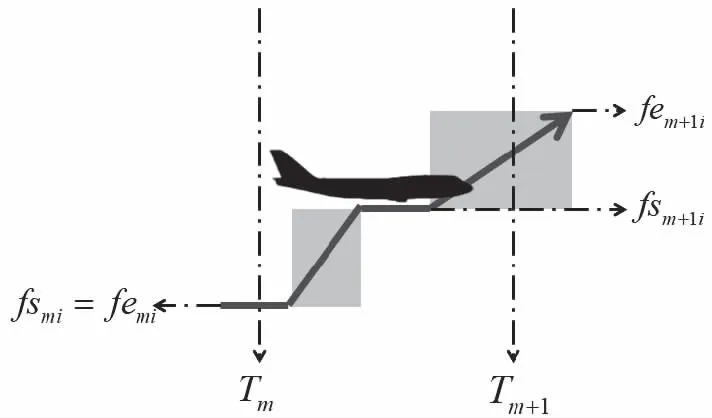
图9 平飞-上升-平飞-上升

为保证Tm与Tm+1时刻之间堆叠相关航空器之间高度层无影响,故所有情况下高度层均应满足

(11)

由于航空器性能原因,飞行过程中应满足其升限,故

(12)

其中fmi为第i架航空器最大飞行高度层。

航空器在进入下一管制单位前,应保持平飞状态

Ti-Tli>tlii

(13)

其中Ti是第i架航空器过移交点进入下一管制单位时间,li是第i架航空器在区域内最后一个堆叠相关时刻的时序。

航空器进入下一管制单位高度应满足下一管制单位因落地需求或其他空域用户活动而提出的高度要求

(14)

其中rui为第i架航空器最高移交高度,rbi为第i架航空器最低移交高度。

2.5 指标函数

在飞行过程中,航空公司会根据航班起飞目的地机场和机型制定符合运行成本的计划巡航高度,频繁改变高度会增大飞行员工作负荷,从而导致人为因素差错。为保证生成垂直航迹冲突解脱策略高效和便捷,指标函数的设置应考虑以下要求:

1)使航空器在避让飞行冲突和满足高度限制的情况下,尽量少地偏离计划巡航高度;

2)尽量减少航空器因高度层改变带来的经济和操作负荷影响;

3)对于第i架航空器管制区内整个飞行剖面,可根据以上七种情况,将航空器在时隙m至m+1之间的经济与人力损失量化。

εi(fp,fa)为第i架航空器偏离适航高度平飞单位时间带来的损失,其中fp为第i架航空器计划适航高度,fa为当前实际飞行高度。

ηi(fs,fe)为第i架航空器高度层从fs改变至fe整个过程带来的经济及人力操作损失。

总罚值θ为所有航空器罚值加总

ηi(fsmi,femi))*(Tm+1i-Tm+1i)

(15)

其中n为管制区内全时域航空器总架次。

3 仿真背景

以西南地区某高空管制空域为实验背景,在5分钟内随机生成40架进入区域航空器模拟航班交通流,该区域日常运行大流量下区域内同时存在航空器很少多于此数量,其负荷已超过正常管制员所能承受。

航空器飞行航径如图10所示

3.1 参数设置

该高空管制单位最低管制权限高度为8400m(含),由于目前国内民航运输航空器机型主要为A320/B737系列,实用升限对应高度层为11000m(含),故设置fs,fe∈[8400,11000],其中包含8个高度层。

航空器地速设置为760km/h至900km/h之间。

为模拟极端情况,制造更多潜在冲突,将所有航空器适航高度都设置为9500m,所有水平航迹相关航空器,均有倾向采取同高度,从而产生飞行冲突。时域内飞行航迹如图11所示。

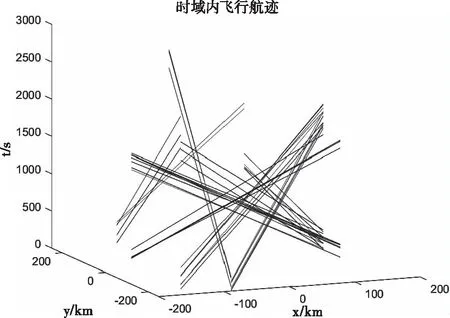
图11 所有航空器时域内飞行航迹

水平冲突探测后,所有航空器共产生74个飞行冲突。

3.2 结果分析

所有航空器在时域内高度调整次数如表1所示

表1 航空器调整次数

区域内航空器经高度层调整规划出无冲突垂直航迹,模型有效。

区域内航空器堆叠数量与时间的关系如图12所示。

图12 全区域时域内堆叠数量

至1945秒所有航空器水平范围不再相关,航空器相互远离分散。在此期间于第1459秒区域内航空器处于最高堆叠状态,共有26对航空器相互堆叠。由于高度层共有8个,显然为每个航空器配备一个高度是不可能的,可以推测此时26对航空器并不处于同一冲突团内,很有可能处于很多相互独立的冲突团内,相互独立的冲突团之间同时刻可使用同样的高度资源。

在此提出相关冲突团概念,若航空器之间直接或间接处于堆叠相关状态,则视为航空器处于同一冲突团,如图13所示。

图13 航空器堆叠相关状态

三架航空器处于同一冲突团。反之则冲突团相互独立。由于相互独立的冲突团可以分别使用同样的高度资源,可以增大解脱策略可行域范围,也可以通过将全局问题拆解为冲突团下独立问题以降低运算量,增强效率,如本次仿真实验中,第1459秒下相关矩阵可最多拆解为6个相互独立相关矩阵,其中最大矩阵宽度6×6,明显优于直接求解40×40矩阵。而在高度分配前的水平航迹规划中,保证后期高度分配有可行解,可使航迹规划后单个冲突团最大航空器数量作为约束条件,从而使得TBO垂直与水平冲突解脱策略更完备。

4 结论

本文提出了一种在航迹已确定后,通过在时域内灵活分配高度层实现冲突解脱的方法,该方法可作为TBO垂直与水平冲突解脱策略结合的前置。为生成这一解脱策略,本文首先提出航空器堆叠概念,将航空器水平间隔低于标准视为可容忍,并记录下加入和离开时刻建立时序,并对该时序下航空器相关性建立矩阵。然后分类研究了相邻时刻间航空器的状态,并针对航空器自身飞行能力限制,最后设置了相应约束模型,讨论并建立了指标函数,完成了模型的建立。

以西南地区某高空管制区域为背景实施仿真实验。实验结果表明模型在大流量多冲突下可有效规划无冲突垂直航迹,模型经验证有效,可采用高度调整的方式应对超过正常管制负荷的空中交通态势。同时数据表明航空器数量或冲突数量并非空域内冲突复杂程度主要因素,直接决定空域内冲突解脱策略求解难度的是时域内所有航空器相关矩阵拆解为最多数量冲突团相关矩阵后,其中最大冲突团的矩阵宽度。从而得出航迹重规划作为高度层灵活调整的前置行为,应将航迹重规划后的最大冲突团航空器数量限制作为约束条件设置入模型中,这个条件相对于所有航空器全水平避让更为宽松,但也满足了高度避让有可行解,且运算效率也更高,可以生成更经济更高效的航迹。

本文提出并建立高度层可变TBO模型经验证有效,可作为水平冲突解脱策略的补充,以期生成更完整立体的冲突解脱策略,同时为水平解脱约束松绑,合理利用空域资源,得到更优化的飞行航迹。