新型节圆正弦蜂窝面内压缩力学性能研究1)

冯学凯 王宝珍 巫绪涛 王 选 郭 煜

(合肥工业大学土木与水利工程学院,合肥 230009)

引言

特殊设计的胞元构型可使蜂窝呈现出诸如负泊松比[1-2]和负刚度[3-4]等不同于传统材料的力学特性.与传统蜂窝材料相比,负泊松比蜂窝通常具有更高的比强度和比刚度、更好的抗冲击性能和抗侵彻性能[5-7],因而在汽车业、包装业、航空航天及军事工程等诸多领域备受青睐.研究者们设计了各种构型的负泊松比蜂窝,其中较为典型的有内凹六边形、星形、手性和双箭头型等[8-11].一些研究者还发现由两种典型构型形成的复合胞元构型可使蜂窝获得更优良的力学性能,例如,Hu 等[12]将内凹结构设计理念用到反手性蜂窝设计中,用以提高蜂窝的承载能力.Wang 等[13]则将双箭头型引入到星形蜂窝中,得到了一种应力-应变曲线具有双平台特征的新型蜂窝,其在低速至高速冲击时都具有负泊松比效应,且冲击吸能性能得到了提高.

然而,上述蜂窝的胞壁均为直壁,在受载时直壁间的节点易出现应力集中问题,曲壁设计则可很好地改善这一问题[14-15].Lee 等[16]发现啄木鸟喙上的波浪形多孔微观结构在巨大冲击力下可保护头部.Liu 等[17]受龟壳结构的启发,将常规反四手性蜂窝的面外直韧带用弯曲的韧带代替,并发现增大弯曲韧带的曲率可明显提高蜂窝的平台应力及吸能能力.Qi 等[18]将内凹蜂窝的直斜壁改为双弧形的曲壁后,变形早期负泊松比效应更为明显,且抗压强度和吸能能力都得到了提高.Zhang 等[19]将两种开槽的圆弧拼接波浪型板正交装配,得到的新型负泊松比反手性蜂窝吸能性能随着圆弧半径和板厚的增大而增大.Guo 等[20]用椭圆胞壁取代十字形反手性蜂窝的直壁,通过数值模拟研究了几何参数对椭圆蜂窝面内压缩性能的影响,并发现椭圆蜂窝的双平台特征与其胞元变形过程密切相关,由此推导了双平台应力的理论解.

正弦曲线数学表达式简单,用于蜂窝中便于优化设计.早在2007 年,Doll 等[21]设计了一种具有负泊松比效应的正弦曲线内凹结构的药物洗脱支架,发现其周向强度刚度高于常规支架.邓小林等[22]通过数值模拟研究了正交正弦蜂窝(OSH)的面内冲击力学性能,并发现负泊松比OSH 有比常规六边形蜂窝更好的冲击吸能性能,并研究了振幅和韧带厚度对OSH 冲击力学响应的影响.Li 等[23]通过对花生形多孔结构进行轻量化简化,也提出了类似的OSH结构,通过实验和理论分析研究了该结构的弹性性能.Chen 等[24]发现改变正弦曲线的振幅及胞元内的周期数目,可实现对OSH 泊松比的调控,使其在-0.7～0.5 范围内变化,且能获得良好的抗振性能.

此外,研究发现引入薄壁圆环可进一步改善一些蜂窝的力学性能.Lu 等[25]在星形蜂窝中引入薄壁圆环使其与星形的四个凹角点相接触,新设计的星形-圆环蜂窝既能保持负泊松比效应,又能获得更优的吸能性能,这与引入圆环后的胞元的变形机制相关.Yang 等[26]和Zhang 等[27]将薄壁圆环插入到正交直壁手性蜂窝的节点中,结果发现由于圆环节点的引入其面外和面内吸能性能都得到了提高.

基于以上研究,本文在OSH 的基础上,用薄壁圆环替换原有节点,提出了一种新型节圆正弦蜂窝(CSH).通过实验和数值模拟分析了OSH 和CSH 的准静态压缩过程,用以验证数值模拟方法的有效性.数值模拟研究了低速冲击下胞元几何参数对CSH面内压缩性能的影响,低速冲击下CSH 具有稳定的双平台特征,且平台的长度和幅值可由胞元几何参数进行调节,这为复杂载荷环境下设计多级吸能防护装置提供了新思路[28].双平台特征与CSH 胞元不同阶段的变形模式有关,由此理论推导了CSH 的双平台应力.最后,讨论了冲击速度对CSH 变形模式,泊松比及冲击吸能性能影响,并将其与OSH 进行了对比.

1 节圆正弦蜂窝设计

OSH 和CSH 的胞元构型分别如图1(a)和图1(b)所示.实际上,OSH 也可视为CSH 在r=0 时的一个特例.为准确描述正弦韧带,建立如图1 所示的局部坐标系oxy,正弦曲线可表示为y=Asin(2πx/l),这里A为正弦曲线的振幅.l为胞元的长和高.此外,几何参数还包括胞壁厚度t及节圆半径r,这里假定所有胞壁厚度相同.定义3 个无量纲几何参数: α=A/l,β=t/l及 γ=r/l.为确保韧带之间不相互重叠,需满足: 4 α+2β ＜1 且 4 γ+2β ＜1.

图1 OSH 和CSH 的胞元构型Fig.1 The unit cell configuration of OSH and CSH

根据多孔材料理论,CSH 结构相对密度表示为

式中,ρ*为蜂窝结构的表观密度,ρs为基体材料的密度,s为x∈(0,l/4) 被节圆截断后单个正弦韧带对应的弧长,如图1(b)中所示,在此范围内,若正弦曲线y=Asin(2πx/l) 与圆x2+y2=r2的交点坐标为 (x0,y0),则s可由下式计算

因上式无解析解,可采用Matlab 数值软件进行计算.图2 给出了OSH (此时 γ=0)与CSH (取γ=0.1)的相对密度与无量纲参数 α 与 β 之间的关系图.

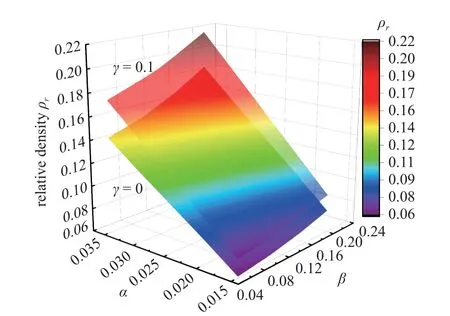
图2 CSH 的相对密度随 α 和 β 变化关系Fig.2 The relative density of CSH varies with α andβ

2 有限元数值模拟分析

2.1 有限元模型

本文采用显式动力学有限元软件LS-DYNA 对CSH 的面内冲击压缩过程进行数值模拟,建立如图3所示的有限元模型.除2.2 节实验验证的数值模拟部分外,其他所有算例中,CSH 胞元的初始长和高均选用l=20 mm,完整CSH 试样由水平方向(X轴方向)和竖直方向(Y轴方向)各6 个胞元排列组成,试样长和高为LX=LY=120 mm,基体材料为铝合金Al6063-T5,采用理想弹塑性模型,并用Cowper Symonds 模型来考虑其应变率敏感性,材料参数参照Liu 等[29]的工作,如表1 所示.

表1 铝合金Al6063-T5 的材料参数[29]Table 1 Material parameters of Al6063-T5 aluminum-alloy[29]

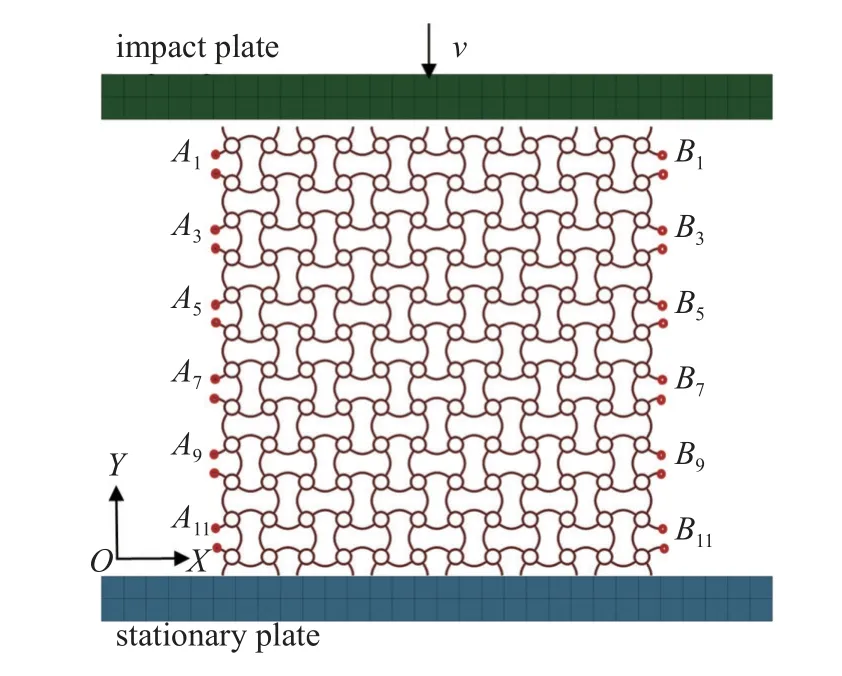
图3 有限元模型Fig.3 Finite element model

其中,σd和 σs分别表示基体材料的动态和准静态屈服应力.是von-Mises 等效塑性应变率,用来表示基体材料的应变率敏感性.D和n为表1 中材料常数.CSH 置于两刚性板之间,下方刚性板固定,上方冲击板与试样之间预留2 mm 的间隙,并向下以恒定的速度v冲击压缩试样,为防止冲击过程中蜂窝发生面外屈曲,对其面外位移进行约束.蜂窝胞壁选用SHELL163 单元进行网格划分,单元尺寸为0.5 mm,为保证计算时的准确性和收敛性,沿厚度方向定义5 个积分点.刚性板与蜂窝之间采用面面自动接触算法,摩擦系数设置为0.2,为防止计算过程中发生穿透现象,蜂窝自身采用单面自动接触算法[30],且不考虑蜂窝内的摩擦.

2.2 数值模拟方法的试验验证

为了验证数值模拟方法的有效性,本文采用熔融沉积成型的方法使用聚乳酸(polylactic acid,PLA)进行3D 打印,制备OSH 和CSH 试样.两种试样的长LX和高LY都为 6 0 mm,面外厚度b为 2 5 mm,胞元尺寸参数为:l=20 mm,A=2.5 mm,t=1.1 mm.CSH 的节圆半径r=2 mm.两种试样通过HY-0350 电子万能材料试验机进行准静态压缩试验,加载速度为6 mm/min,试验机载荷量程为 3 kN.

在LS-DYNA 中对OSH 和CSH 的准静态压缩进行数值模拟,图4 给出了PLA 材料在单轴拉伸下应力-应变曲线,数值模拟时采用理想弹塑性本构模型对其本构关系进行简化.其中,弹性模量为E=2.25 GPa,屈服强度 σs=30 MPa.此外,PLA 的密度为 ρ=1.25 g/cm3,泊松比 ν=0.26.为减少计算时间,顶部刚性板的加载速度v=1 m/s,比实验中采用的加载速度要大得多,但数值模拟结果显示整个加载过程结构总动能少于变形能的5%,故在此速度下可认为试样仍处于准静态加载状态[31].实验和数值模拟得到的应力-应变曲线如图5 所示,应力σ=F/(LXb),应变 ε=ΔLY/LY.这里F为加载端的作用力,ΔLY为上端加载平台的位移.从图5 可以看出,数值模拟结果和实验结果有较好的一致性.对比OSH 和CSH 的应力-应变曲线可以看出,增加节圆后,CSH 表现出很明显的双平台特征,且第2 平台远远高于第1 平台,而OSH 两个平台期区分不明显,两者幅值相差较小.

图4 单轴拉伸下 PLA 应力-应变曲线Fig.4 Stress-strain curve of PLA under uniaxial tensile

图5 实验和数值模拟的应力-应变曲线Fig.5 Experiment and Simulation stress-strain curves

图6 为实验和数值模拟得到在不同应变时的变形图,两者也有很好的一致性.可以看出,开始阶段,CSH 中的节圆几乎无变形,OSH 和CSH 中相邻的呈内凹“)(”状态的正弦胞壁互相靠近,试样左右两侧向中心均匀收缩,表现出较为明显的负泊松比效应,如图6 中 ε=0.13 时的变形模式,之后相邻胞壁会接触到一起,该阶段处于应力-应变曲线的第1 平台期.继续压缩,CSH 中的节圆仍无明显变形,OSH和CSH 中的变形从上下两端开始往试样中部发展,试样左右两侧呈内凹“)(”形,负泊松比效应仍十分明显.观察胞元变形,则表现为水平正弦韧带逐渐伸直,竖直正弦韧带逐渐弯曲折叠成“ ⊃ ⊂ ”形.在ε=0.38,CSH 的水平韧带大多已处于伸直状态,而OSH 中的水平韧带仍基本保持弯曲,说明OSH 的水平韧带伸直变形期更长,从图5 中的应力-应变曲线可知该变形期处于第2 平台期,因CSH 更快完成水平韧带伸直的过程,故其第2 平台期更短,这恰与应力应变曲线的特征相符.进一步压缩,OSH 的水平韧带将进一步伸直,竖直韧带进一步折叠,最终所有韧带压溃堆积一起,进入密实状态,如OSH 在ε=0.65时的变形模式.CSH 则表现为节圆被压扁,呈椭圆状,因其抗压强度较高,在应变约为0.5 时,试验机接近最大量程故停止加载.

图6 OSH 与CSH 实验和数值模拟的变形历程Fig.6 Deformation process of OSH and CSH experiment and numerical simulation

3 低速冲击下CSH 的面内压缩力学响应

保持CSH 的无量纲几何参数 β=0.025 及γ=0.1不变,改变 α 值,按2.1 节介绍的有限元模型在冲击速度v=2 m/s 下对CSH 试样进行面内低速冲击压缩数值模拟.

3.1 变形模式

图7 给出了 α 为0.05,0.1,0.125 时CSH 在不同应变时的变形模式图.可以看出,在开始阶段(ε=0.1),α=0.10 和 α=0.125 时,CSH 试样横向均匀向内收缩,α=0.05 时,不仅整体横向收缩,其中上部还出现颈缩现象,3 种试样都表现出明显的负泊松比效应.继续压缩(ε=0.3),试样左右两侧都呈“)(”内凹形态,α 越小,内凹程度越大,负泊松比效应越明显,观察胞元可以看出,胞元中的正弦胞壁靠近并接触在一起.继续压缩,α=0.10 的蜂窝中上部出现“˄”形和下部出现倒“˄”形变形带,α=0.125 的蜂窝表现出“X”形变形带,且CSH 试样单侧表现出隆起趋势.进一步压缩,不同 α 蜂窝都表现出一侧出现明显的隆起效应,一侧向内收缩,直至蜂窝进入密实化.

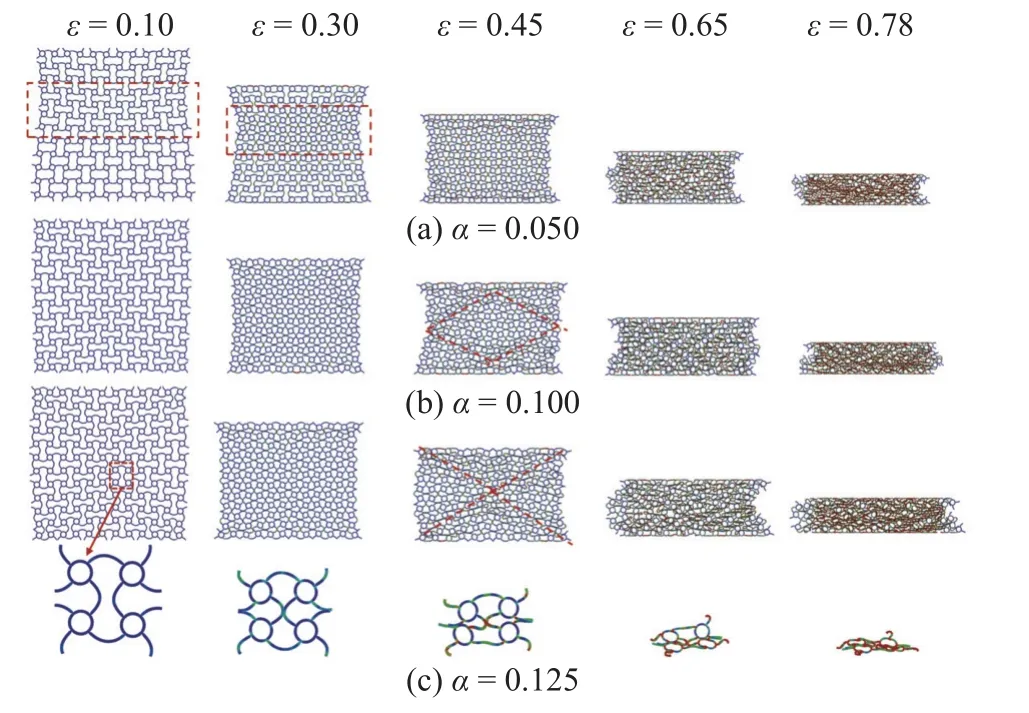
图7 冲击速度为2 m/s 时不同 α 值CSH 的变形模式Fig.7 Deformation modes of CSH with different amplitude ratios at the impact velocity of 2 m/s

尽管 α 不同,CSH 试样整体变形模式有所不同,但观察胞元的变形特征,发现其变形机制有一定的相似性.故图7(c)中还选择了一代表性胞元给出了不同应变时的变形模式图.不讨论弹性变形阶段,可以看出,胞元变形主要分为4 个阶段: 第1 阶段,节圆无变形,内凹胞壁向胞元中心靠近,并最终接触在一起,如 ε=0.1 和 ε=0.3 的胞元变形图;第2 阶段,节圆仍无明显变形,水平韧带拉直,竖直韧带从 “)(”形弯曲折叠为“ ⊃ ⊂ ”形,如ε=0.45 的胞元变形图;第3 阶段,节圆压扁变为椭圆形,上下相邻椭圆形节圆胞壁接触,如 ε=0.65 的胞元变形图;第4 阶段,所有胞壁全部坍塌堆积密实,如 ε=0.78 的胞元变形图.

3.2 应力-应变关系

图8 为不同 α 时CSH 的应力应变曲线,可以看出,CSH 的应力应变曲线表现出明显的双平台特征,且随着 α 的增大,第1 平台期缩短,而第2 平台期加长.

图8 不同 α 时CSH 的应力-应变曲线Fig.8 Stress-strain curves of CSH vary withα

能量吸收效率E(ε) 曲线常被用来确定蜂窝应力-应变曲线各阶段的起始应变及终止应变,从而准确计算各阶段平台应力.E(ε) 可由下式计算

图9 给出 α=0.125 时的应力-应变曲线计算得到的能量吸收效率曲线,初始应变和结束应变可由该曲线的极小值和极大值对应的应变给出.ε01为弹性阶段结束应变,即应力-应变曲线中初始峰值应力对应的应变.从能量吸收曲线可知,存在多处局部极大值和极小值,前两个平台段的起始应变 ε02和结束应变 εp1和 εp2分别对应能量吸收曲线中的极小值点和极大值点.而最后一个极大值点对应的应变常被定义为密实应变 εd.实际上,在第2 平台阶段后还有一个应力幅值较高但非常窄的 “第3 平台”阶段,但此时CSH 因经历较大压缩变形后相对密度较大,应力幅值难以保持恒定而呈上升趋势,故这里将第2 平台结束应变 εp2到密实应变 εd统称为“应力增强阶段”.故CSH 的应力-应变共包含5 个阶段,即线弹性段、第1 平台段、第2 平台段、应力增强阶段及密实阶段,如图9 所示.

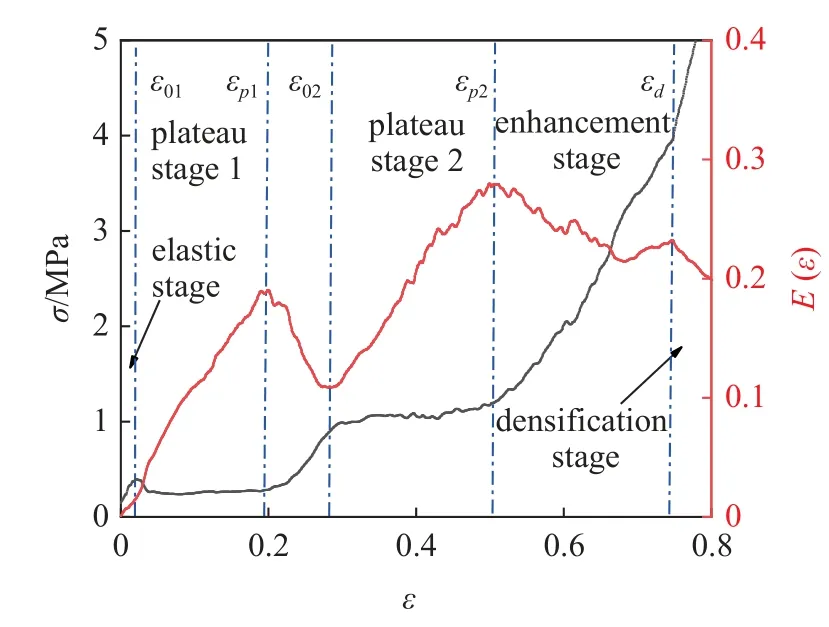
图9 CSH 的应力-应变及吸能效率曲线(α=0.125)Fig.9 Stress-strain and energy absorption efficiency curves of CSH (α=0.125)

第1 平台应力 σp1和第2 平台应力σp2可由下式计算

两平台应力计算结果如图8 中水平点线所示,可以看出,尽管 α 增大,CSH 的相对密度增大,但两个平台应力 σp1与 σp2都随之降低,即平台应力与α呈负相关性.

3.3 双平台应力的理论分析

应力-应变曲线的阶段性特征与胞元的变形机制有关,这里不考虑弹性阶段,前述提到胞元的4 个变形阶段正好对应应力-应变曲线的后4 个阶段.取前两个阶段胞元的变形模式进行理论分析,推导CSH 的双平台应力,为此,构建了代表性胞元的理想变形模式图如图10 所示.胞元初始长度l0与高度h0均为l,内凹波峰D、与节圆中心O的倾角θ0=arctan(4α).假定压缩过程中胞壁厚度t及曲壁长度s保持不变.在韧带靠近阶段中,1/4 胞元连接处形成塑性铰,共形成16 个塑性铰,如图10(a) 红色圆圈所示,每半周期韧带绕节圆中心旋转,内凹韧带间相互靠近,当胞元外壁上的点C-G,B-L,F-H 接触时,该阶段完成.胞元长度和高度变为l1和h1,可由下式计算

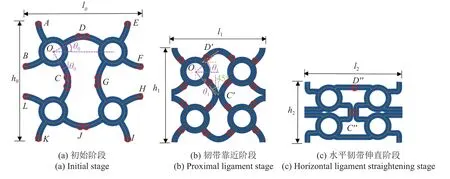
图10 胞元变形图Fig.10 Deformation of a unit cell

此时蜂窝的压缩位移为up1=l-l1,根据能量守恒理论,外力做功等于塑性铰的能量耗散,故有

式中,Mp表示CSH 胞壁的塑性弯矩.对于矩形截面梁Mp=σsbt2/4,结合式(5)～式(7),可得CSH 的第1平台应力理论解为

进一步压缩,CSH 进入水平韧带伸直阶段,该阶段的初始长度和高度分别为l1和h1,韧带上与节圆连接处额外产生16 个塑性铰,如图10(b)所示,故一共形成32 个塑性铰.当胞元水平韧带伸直,竖直韧带弯曲折叠为“ ⊃ ⊂ ”,该阶段完成,此时胞元高度变为h2=4r+2t,相邻的水平和竖直弯曲韧带旋转角度之和为 π/2.

由 σp2bl1(h1-h2)=16Mp(π/2) 可得CSH 的第2平台应力 σp2理论解为

4 分析与讨论

4.1 低速冲击下CSH 的平台应力

选用无量纲几何参数α=0.125,β=0.025 和γ=0.100为参考CSH 模型.在讨论其中一个几何参数的影响时,保持另两个几何参数不变.图11 给出了 α,β 和 γ 对CSH 应力-应变曲线的影响,可以看出所有应力-应变曲线都具有双平台特征,α 增大,第1 平台期变短而第2 平台期加长,β 增大,第1 平台期长度变化不明显,第2 平台期变短;γ 增大,第1 平台期基本没有影响,第2 平台期缩短,特别地,γ=0.125时出现了较为平坦的第3 平台段.按照式(5)可计算得到两个平台应力,它们与几何参数 α,β和 γ 的关系如图12 所示.可以看出: CSH 第1 平台应力和第2 平台应力与 α 负相关,而与 β 正相关,即第1 平台应力 σp1和第2 平台应力 σp2随着 α 的减小和 β 的增大而增大.而 γ 的变化对第1 平台应力几乎没有影响,但对第2 平台应力有很大影响,第2 平台应力随着 γ 的增大迅速增大,从前述CSH 胞元变形机制可很好地解释这一点,第1 平台期,CSH 和OSH(γ=0)的变形机制完全相同,都表现为半周期正弦韧带绕节圆中心或正交节点旋转,从而导致邻近韧带相互靠近,故第1 平台应力与节圆半径无关.第2 平台期胞元变形则以水平韧带被拉直、竖直方向韧带弯曲折叠为“ ⊃ ⊂ ”形为主.引入节圆后,截取后的正弦曲线长度减小,更快完成韧带伸直阶段,又因节圆的约束,胞元的承载能力提高,故随 γ 的增大,第2 平台期变短,第2 平台应力增大.

图11 α,β 和 γ 对应力-应变曲线的影响Fig.11 The effects of α,β and γ on stress-strain curves

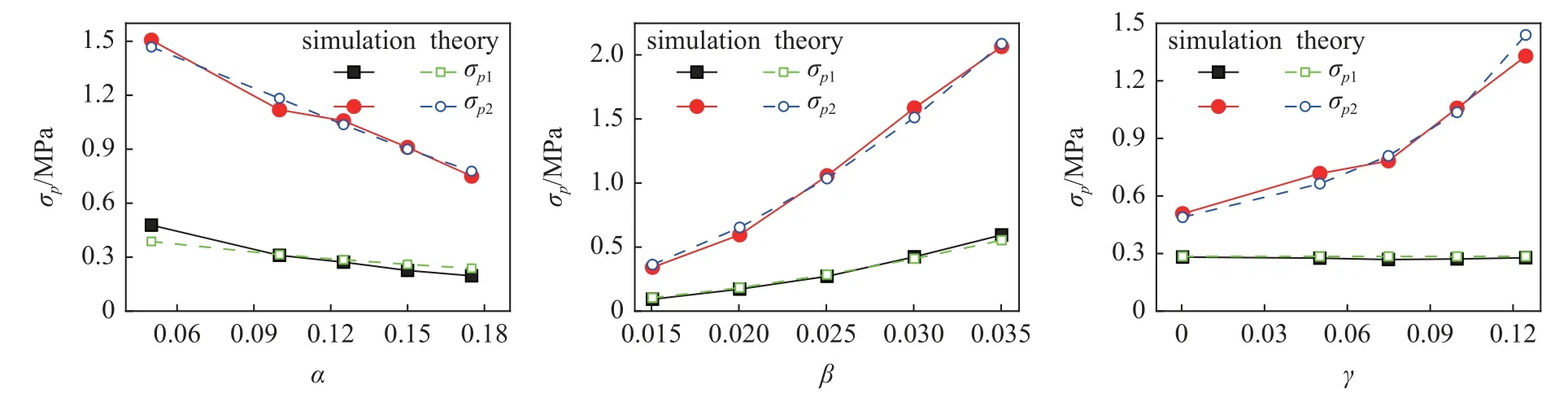
图12 α,β 和 γ 对平台应力的影响Fig.12 The effects of α,β and γ on the plateau stress

此外,图12 还给出了由式(8)和式(10)计算的理论值,可以看出,理论模型得到的两个平台应力与数值模拟计算得到的结果有较好的一致性,说明该理论模型可以很好地预测CSH 的平台应力.

4.2 低速冲击下CSH 比吸能

吸能特性是评价蜂窝力学性能的一个重要指标,常用比吸能(specific energy absorption,SEA)来评估,为了区分不同阶段的吸能能力,定义第1 平台阶段、第2 平台阶段及应力增强阶段的比吸能为

密实前CSH 总的比吸能为

图13 给出了不同阶段比吸能随几何参数的变化.可以发现: 随着 α 的增大,第1 平台和第2 平台阶段比吸能ESEA1和ESEA2逐渐减小,但应力增强阶段比吸能ESEA3呈现出先增大后减小的趋势.当 α 从0.05 增大至0.125 时,密实前总比吸能ESEA变化较小,当 α 继续增加,ESEA大大减小.α 从0.05 增大至0.175 时,ESEA从2.56 k J·kg-1降至1.88 k J·kg-1;β增大,3 个阶段的比吸能及总比吸能都得到提高,当β从0.015 变化到0.035 时,ESEA由1.58 kJ·kg-1升至2.94 kJ·kg-1,提高了0.86 倍;γ 增大,CSH 的第1 平台期比吸能ESEA1减小,但应力增强阶段的比吸能ESEA3在 γ ≥0.10 范围内得到了很大提高,最终ESEA也随之提高.相比OSH(γ=0),γ=0.125 时的CSH总比吸能由 0.86 kJ.kg-1提高至 2.50 kJ.kg-1,提高了1.91 倍.

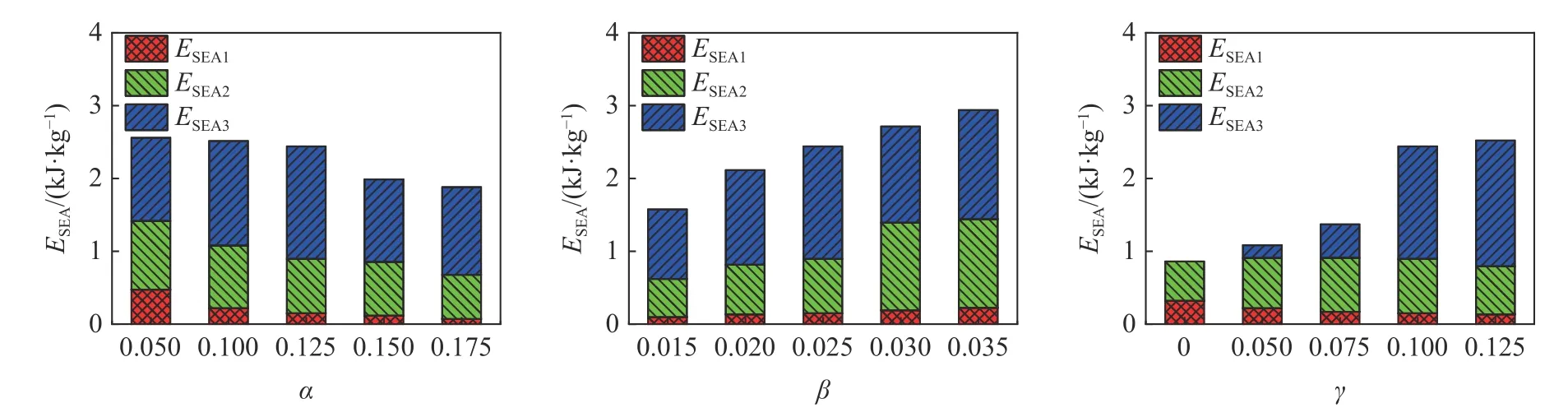
图13 α,β 和 γ 对比吸能的影响Fig.13 The effects of α,β and γ on the specific energy absorption

4.3 不同速度冲击下CSH 的动力学响应

取 α=0.125,β=0.025,γ=0.1 的CSH 为研究对象,给出了冲击速度为 2 m/s,3 0 m/s 及1 00 m/s 下CSH 的应力-应变曲线如图14(a)所示.可以发现,速度提高至 3 0 m/s 时,由于惯性效应,冲击加载初期,应力-应变曲线存在一定的振荡,应力-应变曲线中的第1 平台和第2 平台无法区分,两者形成了一个连续的平台期,其应力幅值与低速加载时的第2 平台应力较为接近,这样应力-应变曲线从低速时的5 个阶段变为4 个阶段,速度继续提高至100 m/s,应力应变曲线仅有一个平台期,且平台期应力幅值绕一恒定值来回振荡,之后应力-应变曲线迅速上升,即高速时应力-应变曲线仅包含3 个阶段.

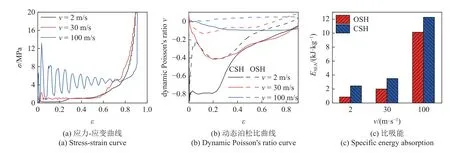
图14 不同冲击速度下CSH 的力学性能Fig.14 Mechanical properties of CSH at different impact velocities

当v=2 m/s 时CSH 的变形图如图7(c) 所示,v=30 m/s 和v=100 m/s 时CSH 变形模式分别如图图15(a)和图15(b)所示.低速(v=2 m/s)冲击下,CSH呈现出整体变形模式,其变形过程前文已陈述,这里不再讨论.当速度增大至v=30 m/s,CSH 宏观变形特征与低速时不同,变形初期,如 ε=0.1 时,由于惯性效应,靠近冲击端附近的胞元相邻韧带相互接近,且同时伴随着水平韧带的拉伸,靠近固定端的胞元则几乎无变形,从而在冲击端形成局部变形带,局部变形带从冲击端向固定端传播,应变约为0.4 时,试样相邻韧带全部接触,上端韧带完全伸直,而中下部水平韧带也轻微拉直,CSH 表现出明显的负泊松比效应,由于胞元的胞壁靠近变形和韧带伸直变形几乎同时发生,故两个平台期合并成一个连续的平台期;继续压缩,CSH 试样多处形成局部变形带,水平韧带全部拉直,竖直韧带折叠后部分发生旋转.进一步压缩,节圆压扁成椭圆状,图14(a)中可以看出,该速度下,在此阶段出现了一个应力幅值约为5 MPa 的平台期.最终,节圆全部坍塌蜂窝逐渐进入密实阶段.速度继续增大至v=100 m/s,惯性效应对蜂窝的变形模式起主导作用.压缩开始,最顶层水平韧带伸直且节圆同时被压为扁平状,第2 层的相邻韧带则向内靠近,而其他层几乎不发生变形,从而在顶端形成近似的“I”形局部变形带,继续压缩,这种局部变形从顶层到底层逐层传播,即试样被层层压溃.这种层层递进的变形方式使得应力应变出现周期性的振荡,应力-应变曲线中12 个周期的振荡恰好与12 层节圆对应.从图15(b)还可发现,即使在v=100 m/s 的高速条件下,CSH 侧向仍有向内的微量收缩,即仍具有轻微的负泊松比效应.

图15 不同冲击速度下的变形模式Fig.15 Deformation modes at different impact velocities

为分析CSH 的负泊松比效应,采集CSH 模型左右两侧12 组对称节点间x方向的位移如图3 所示,通过对各点的位移求平均值得到蜂窝水平位移,即

式中,Ai和Bi为X方向上蜂窝左右两侧代表性对称节点水平位移,CSH 的动态泊松比可由下式计算

式中,εX和 εY为X方向和Y方向的应变.

图14(b)给出了3 种速度下CSH 的动态泊松比曲线,为对比,也给出了OSH 的动态泊松比曲线.可以发现: 在v=2 m/s 时,CSH 泊松比在应力-应变曲线的第1 平台阶段基本保持恒定,约为-0.8,之后泊松比迅速增大,但在应变为0.8 时,仍具有负泊松比效应.速度提高至v=30 m/s,动态泊松比也有一段基本保持恒定,约为-0.4,之后也迅速增大,并在大变形范围内,仍为负值.速度继续提高至v=100 m/s,CSH的动态泊松比在-0.1～0 之间,即在高速下仍具有轻微的负泊松比效应.然而,在低速冲击下,OSH 的泊松比增至-0.4 左右,中速冲击下,OSH 表现出轻微的负泊松比效应,高速冲击下基本不表现负泊松比效应.

图14(c)给出了3 种速度下CSH 和OSH 总的比吸能,发现在低速、中速和高速载荷冲击下,CSH 吸能性能均优于OSH,尤其在中低速载荷冲击下分别提高了1.84 倍和0.75 倍.同时,随着冲击速度的增大,CSH 的比吸能逐渐增大.

5 结论

本文以正交正弦蜂窝构型为基础,在正交节点处引入薄壁圆环,设计出了新型的节圆正弦蜂窝.通过实验、数值模拟及理论分析,系统地研究了几何参数及冲击速度对节圆正弦蜂窝面内力学性能的影响,得出结论如下.

(1) 实验和数值模拟都表明,增加节圆后的CSH 相比于OSH 具有明显的双平台特征,这对于提高蜂窝的承载能力及吸能能力十分有利.实验和数值模拟的一致性,验证了文中数值模拟方法用于研究CSH 面内压缩力学性能是可行的.

(2) 低速冲击下,CSH 胞元在不同变形阶段表现出4 种不同的变形机制,即相邻韧带靠近、水平韧带伸直、节圆压扁和所有胞壁完全坍塌.这4 种变形机制分别对应于应力-应变曲线中的第1 平台期、第2 平台期、应力增强期及密实期.根据蜂窝胞元的变形机制,并基于能量守恒理论,推导得到的双平台应力理论解与数值模拟结果有较好的一致性,说明理论解可预测不同几何参数的CSH 的平台应力.

(3) 胞元的几何参数对CSH 的力学性能有较大影响.CSH 的双平台应力均随着振幅的增大而减小,壁厚的增大而增大;增大节圆半径,CSH 的第2 平台应力显著提高,第1 平台应力几乎不受影响.随着振幅的增大,CSH 的比吸能逐渐减小,但振幅较小时影响较弱.增大胞壁厚度和节圆半径,可显著提高蜂窝的比吸能.

(4) 随着冲击速度的提高,CSH 呈现不同的变形模式,即低速时表现为整体变形模式、中速时表现为局部变形模式、高速时表现为“I”形逐层变形模式.由于冲击速度对胞元变形机制的影响,应力-应变曲线的形态发生变化,低速、中速至高速时应力-应变曲线所分阶段呈递减趋势.CSH 的泊松比随着速度提高而增大,但即使速度提高至 1 00 m/s,仍表现出负泊松比效应.

(5) 对比OSH,CSH 在不同冲击速度下均表现出更优越的力学性能,更明显的负泊松比效应,尤其在低速和中速冲击下冲击吸能性能远远优于OSH.