考虑有界场的几何不确定性非概率可靠性拓扑优化1)
战俊杰 彭秀林 白仲航,†,2)
* (河北省健康人居环境重点实验室,天津 300132)
† (河北工业大学国家技术创新方法与实施工具工程技术研究中心,天津 300401)
引言
拓扑优化作为一种有效的自动化设计工具,已广泛应用于各种结构的设计问题.常用的拓扑优化方法主要包括SIMP (solid isotropic material with penalization)法[1-2]、ESO (evolutionary structural optimization)法[3]、水平集法[4-5]、智能拓扑优化方法[6-7]等.此外,Guo 等[8-12]提出了一种基于移动可变形组件/孔洞的拓扑方法,以可移动可变形组件为基本元件进行结构拓扑优化设计.近期,Luo 等[13-16]提出了一种基于材料场级数展开 (material-field series-expansion,MFSE)的拓扑优化方法,该方法能够有效避免结构中的棋盘格现象及网格依赖性问题,并且能够大幅减少设计变量个数,提高计算效率.
在结构的加工制造及使用过程中,不可避免会存在各种不确定性,比如加工误差导致的几何不确定性,工作时的载荷不确定性等.这些不确定性会使结构产生性能波动和关键指标降低,严重影响结构的安全性.现有处理不确定性的方法主要是基于概率框架进行的.随着概率可靠性优化方法的发展,一些实用的求解策略如功能度量法[17-18],序列优化方法[19]及概率神经网络[20]等都极大地促进了概率可靠性方法在实际工程中的应用.此外,实际工程中的许多不确定性,如分布荷载、几何尺寸、材料属性等,其在空间不同位置上的实现是随空间位置的变化而变化的,这属于“不确定场”问题.目前,常用来描述不确定场的模型为随机场模型[21-23].将制造误差引起的几何缺陷描述为随机阈值场模型,Kang 等[22]提出了一种考虑几何空间不确定性的概率可靠性拓扑优化方法.通过将非侵入式PCE (the polynomial chaos expansion) 方法与设计灵敏度分析相结合,Keshavarzzadeh 等[23]提出了一种随机场几何不确定性下的可靠性拓扑优化的系统方法.
针对工程实际中广泛存在的未知但有界不确定性,由于缺少大量样本数据信息,难以获得不确定性准确地概率分布特征,因此概率不确定性理论不再适用.作为概率可靠性理论的有效补充,研究人员提出了许多描述参数不确定性的非概率模型,比如模糊模型[24-25]、证据理论[26-27]、区间模型及凸模型[28-34]等.Sofi 等[30]通过结合区间运算和安全系数方法,将非概率可靠性指标描述为一个区间变量.Pantelides等[33]提出了一种反优化技术进行考虑载荷不确定性的非概率可靠性的优化设计.将结构边界长度变化描述为凸模型,Luo 等[34]完成了考虑结构几何不确定性的非概率可靠性优化设计,优化后的结构具有更高的可靠性.
至于少样本的场不确定性问题,由于样本数量有限,因此随机场模型也不再适用.通过引入EUI(external unit interval)变量,Muscolino 等[35-36]提出了一种区间场方法来量化未知但有界的不确定场.基于空间相关性的数学定义和非概率级数展开方法,Luo 等[37]提出了一种处理有限样本下不确定场问题的有界场模型.基于有界场模型,Zhan 等[38]提出了一种非概率可靠性指标进行结构场不确定性下的非概率可靠性评估,并进一步完成了不确定载荷场作用下的结构非概率可靠性优化设计研究[39].
文献调研显示,尽管基于参数的非概率可靠性优化方法已应用于结构几何不确定性分析,但针对工程实际中考虑少样本及空间变化特性的几何不确定性,仍缺乏合理的可靠性优化模型.因此,本文将采用阈值技术[40]进行具有空间变化特性的几何不确定性表征,并将Heaviside 过滤函数中的阈值 η 假定为有界不确定阈值场,建立非概率有界场模型,进而完成考虑结构几何不确定性的非概率可靠性拓扑优化设计.
本文的具体安排如下: 首先进行不确定场的非概率描述,即将不确定场描述为非概率有界场模型;第2 节进行结构几何不确定性的描述,即通过不确定阈值场来表示,进而描述为有界场模型;第3 节为建立结构的非概率可靠性优化模型;在第4 节推导了模型的灵敏度信息,并采用移动渐近线法 (method of moving asymptotes)[41]求解优化问题;最后通过2 个数值算例验证了模型的有效性.
1 不确定场的非概率描述
其中Z0(x) 为标准化的不确定场,且满足-1 ≤Z0(x)≤1.
考虑到在实际工程中结构的不确定边界是连续变化的,因此假定有界不确定场Z(x) 的空间波动具有一定相关性.在本文中,设计域 Ωdom内任意两个观察点xa和xb对应的不确定场的相关性通过相关函数R(xa,xb) 来描述,R(xa,xb) 的表达式为
其中,符号 ‖·‖表示2 范数.L是不确定场Z(x) 的相关长度,它用来控制不确定场的空间波动程度.当相关长度L较小时,不确定场的空间波动较为剧烈,L=0表示所有观察点处的变量都是不相关的;当相关长度L较大时,波动较为平缓,L→+∞ 表示不确定场完全相关,即所有观察点处的不确定场值Z(xi) 均相等.
设计域内各观察点之间的相关性构成了相关矩阵R,因此R表示为
基于非概率级数扩展,标准化的不确定场Z0(x)可表示为
在式(4)中,特征值 λj为降序排列,特征值越小的项对不确定场的贡献值越小.因此,为提高模型的计算效率,可对式(4)进行截断,仅保留前M项,即通过M个不确定系数(ξj(j=1,2,···,M))来描述不确定场.截断公式可表示为
其中,α 是一个很小的值.在本文中,α=1.0×10-6.
对式(4)进行截断后并代入式(1)中,可得到不确定场的表达式为
已知标准化的不确定场Z0(x) 的变化范围为Z0(x)∈[-1,1],得
对式(7) 两边平方,并写成向量的形式,可以得到
2 几何不确定性的描述
在现有的拓扑优化设计中,Heaviside 过滤技术已得到了广泛的应用.与敏度法和密度法过滤相比,优化的结构经Heaviside 过滤可获得清晰的结构边界.本文用到的Heaviside 过滤函数定义为
其中,不确定系数 ξj的变化范围如式(9)所示.
为了进一步说明不确定阈值场 η (x) 对结构不确定性的影响,图2 以MBB 梁为例分别给出了不确定阈值场 η (x) 和确定阈值 η (x)≡0.5 对结构边界的影响.从图2 中可以看出,与阈值为恒定值(η (x)≡0.5)相比,当阈值描述为不确定场时,结构的边界会存在一定的扰动(认为是几何不确定性).
3 考虑几何不确定的结构非概率可靠性拓扑优化模型
3.1 考虑不确定阈值场的结构非概率可靠性指标
正如第2 节描述的那样,不确定阈值场 η (x) 会对结构的边界产生影响,进而影响结构的性能.因此,结构性能可表示为不确定阈值场 η (x) 的函数.在本文中,结构的性能函数可表示为C(η)≤C*,其中C为结构的柔顺性,C*为给定的柔顺性约束.令g(η)=C*-C(η),则g(η) 称为极限状态函数.
由式(6)可知,不确定阈值场 η (x) 是关于不确定系数 ξ 的函数.因此,在不确定系数 ξ 的空间中,极限状态函数g(η) 可进一步表示为G(ξ)=g(η(ξ,x)).
依据有界不确定场的非概率可靠性指标的定义[39],极限状态函数G(ξ) 可将不确定系数 ξ 空间划分为可靠区和失效区,如图3 所示(为便于表示,示意图中只考虑了2 个不确定性系数 ξ1和 ξ2).因此,考虑几何不确定性的结构非概率可靠性指标定义为
即表示在可靠区域内所允许的最大不确定性.其中,式(11)的最优解 β*为非概率可靠性指标.jud(G(0))用来判断可靠性指标 β*的正负,具体的表达式为
3.2 基于MFSE 模型的拓扑优化方法
为避免传统密度法拓扑优化中的棋盘格现象及网格依赖性问题,本文将采用基于MFSE 的拓扑优化方法[13].在本方法中,结构拓扑通过一个具有一定空间相关性的有界材料场函数φ(y)∈[-1,1],y∈Ωdom来描述.经材料场级数展开,并进行截断保留前Me(Me≤N)项,则场函数 φ (y) 可表示为
其中,κk和 ψk为相关矩阵 Γ 的特征值和特征向量.相关矩阵 Γ 的表达式为
类似于前面不确定场的处理方式,依据有界不确定场函数 φ (y)∈[-1,1] 的界限并引入符号Hm=κ-1/2ΨTΓD(ym)ΓD(ym)TΨκ-1/2,则式(13) 可转化为如下形式
在本方法中,假定结构的单元中心与不确定场函数 φ (y) 的观察点ym一一对应.单元的插值函数可表示为
基于MFSE 的结构柔顺性拓扑优化问题可表示为
3.3 结构非概率可靠性优化模型
在本文中,结合MFSE 优化模型(式(17))及考虑不确定场的可靠性指标(式(11)),考虑结构几何不确定性的非概率可靠性拓扑优化问题可表示为:在结构体积一定的情况下使结构的可靠性指标最大化,进而来提高结构的可靠性,优化列式如下所示
需要注意的是,在式(18)的外层优化中,很难准确地获得可靠性指标 β*对设计变量χ的灵敏度信息.因此,可采用关心性能法[34,39]对式(18)进行等效变换.基于关心性能法(详见文献[34,39]),式(18)的非概率可靠性拓扑优化问题可以转化为
其中,内层优化为获得在外层设计变量为χ时的关心性能值 σ (χ,ξ*),ξ*称为关心点.确定了关心点 ξ*后便可得到此时对应的不确定阈值场 η (x) (依据式(11))分布情况.极限状态函数G(χ,ξ) 是结构柔顺性的函数,表示为G(χ,ξ)=C*-C(χ,ξ).由于C*为一给定常数,因此式(19)中外层优化的目标函数maxG(χ,ξ*)可等效表示为 m inC(χ,ξ*);内层优化等效为 maxC(χ,ξ).为给定的非概率可靠性指标下限值.
本文采用移动渐近线方法(MMA)[41]求解该非概率可靠性优化问题.优化模型的收敛准则定义为变量(内层为变量 ξ,外层为变量χ)在相邻两步迭代中的最大变化值小于0.01.
4 灵敏度分析
4.1 极限状态函数对不确定系数的灵敏度分析
本文考虑几何不确定性的非概率可靠性优化问题是基于梯度算法求解的,因此灵敏度分析是必不可少的过程.该优化模型(式(19))为嵌套优化,首先求解内层优化的灵敏度信息,即极限状态函数G(χ,ξ) 对不确定系数 ξj的灵敏度分析.具体求解过程如下所示
平衡方程Ku=F两边对不确定阈值场 η (xi) 求导,并等式变换,得
4.2 关心性能值对设计变量的灵敏度分析
优化模型中外层优化主要涉及的灵敏度为关心性能值 σ 对设计变量χk的灵敏度分析,为实现优化模型的解耦,假设关心性能点 ξ 对设计变量的灵敏度为0.因此,其表达式为
其中,关心性能点 ξ*为优化模型内层的最优解.
依据链式法则,式(24)表示为
引入伴随向量 γ,式(27)表示为
依据式(16)的插值函数,可得到
在单元层面上,关心性能值 σ 对设计变量χk的灵敏度可表示为
4.3 非概率可靠性拓扑优化流程图
为便于理解式(19)的非概率可靠性拓扑优化模型,图4 给出了优化过程的流程图.优化过程为嵌套优化,其中右侧为内层优化,目的是得到在几何不确定性下的关心性能值,求解过程涉及极限状态函数G(χ,ξ) 对不确定系数 ξj的灵敏度分析(第4.1 节内容);左侧为外层优化,即在给定体积约束下获得结构的最优拓扑,求解过程涉及关心性能值G(χ,ξ*) 对设计变量χk的灵敏度分析(第4.2 节内容).
5 数值算例
本节给出了2 个数值算例来验证本文提出的考虑几何不确定性的非概率可靠性优化模型的有效性.对于这2 个算例,结构的弹性模量和泊松比分别为E0=2.0×105MPa 和υ=0.3.在整个优化过程中,结构始终处于线弹性阶段.这2 个算例都是Windows 10 操作系统性下基于MATLAB 软件计算的,电脑的配置为AMD Ryzen Threadripper PRO 5965 WX 24-Cores 3.80 GHz,128 GB RAM.
5.1 MBB 梁结构的非概率可靠性优化
如图5 所示为半个MBB 梁结构,结构的尺寸为140 mm×70 mm,整个设计域离散为140×70(9800)个平面应力单元.结构右下角约束了Y方向的位移,左边约束了X方向的位移.集中载荷F=100 N 垂直作用于结构的左上角,方向为-Y方向.不确定阈值场的范围为 η (x)∈[0.25,0.75],在本算例中考虑了不确定阈值场2 种不同的相关长度,即L=80 mm 和L=30 mm.此外,还讨论了2 种不同的可靠性指标约束(=1.0 和=1.5)对拓扑结构的影响.本算例给定的结构体积分数为f=50%.
作为对比,首先给出了本算例的确定性优化结果,即不确定阈值场 η (x)≡0.5 的情况(等价于相关长度L→+∞ 时的阈值场),优化结果如图6 所示.考虑不确定阈值场的结构非概率可靠性拓扑优化结果如图7 所示.通过对比非概率可靠性优化结果(图7 左列)与确定性优化结果(图6),可以看出非概率可靠性优化的最优拓扑构型与确定性优化的不同,并且非概率可靠性优化的最优解是通过增加更多的肋来保证结构在不确定阈值场下的可靠性.
此外,图7(a)和图7(b)为考虑了不确定阈值场η(x)相 同的相关长度(L=80 mm),但优化模型(式(19))的可靠性指标约束值不同(=1.0 和=1.5).对比这两个工况,可以看出非概率可靠性拓扑优化结果存在一定差异(如图7(a)和图7(b)左列),即结构中的“杆件”数量和位置存在明显不同.另外,当 β 不同时,尽管关心点处的不确定阈值场空间分布波动情况类似,但不确定场 η (x) 的空间波动范围会随着可靠性指标约束值的增大而增大: (1)=1.0 时,波动范围是 [ 0.34,0.75] (如图7(a)右列);(2)=1.5 时,波动范围是 [ 0.19,0.87] (如图7(b)右列).优化结果存在差异的原因在于,随着可靠性指标约束值的增加,进行结构的可靠性设计时考虑的几何不确定性范围更大,关心点处不确定阈值场的波动范围也会更大(如图7(a)和图7(b)右列).同时,由于考虑了更多的不确定性,那么设计的结构可靠性会更高,最优的拓扑构型也会相应地发生变化(如图7(a)和图7(b)左列).此外,不确定阈值场 η (x) 的分布特点基本满足在结构左侧区域数值较大,右侧区域数值较小的特点.
不同情况下的考虑几何不确定性的非概率可靠性优化模型计算时间如表1 所示.其中,内层优化和外层优化的计算时间均为迭代一次的平均时间,内层优化的迭代步数为30 步左右,外层优化迭代为150 步左右.从表1 中可以看出,当不确定阈值场的相关长度较小(L=30 mm)时,内层优化需要的时间更长(23.360 4 s).这是因为当相关长度较小时,则需要更多的截断项才能保证要求的不确定场截断精度(式(5)),那么式(19)中内层优化中的变量数(ξj)会更多,计算时间也会相应地增加.
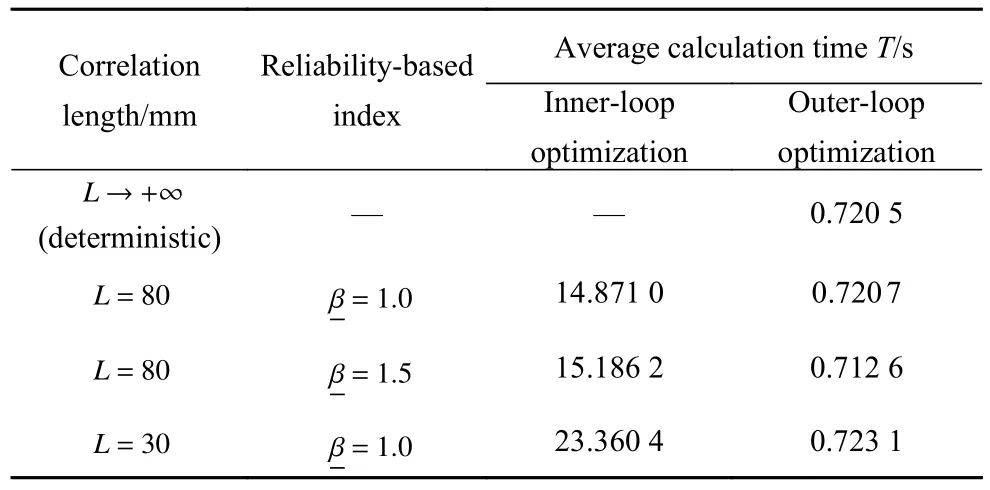
表1 不同情况下非概率可靠性优化模型计算时间Table 1 The computing time of non-probability reliabilitybased topology for different cases
为了说明优化结果的正确性,我们将通过差分灵敏度分析法来验证第4 节的解析灵敏度分析的正确性,差分法采用的差分步长为0.001.以L=80 mm,=1.0的工况为例,内层优化共包含25 个不确定系数 ξj(j=1,2,···,25),随机选取4 个不确定系数(ξ2,ξ5,ξ10,ξ15) 进行灵敏度对比,对比结果如表2 所示.外层优化同样随机选取4 个设计变量(χ2,χ10,χ30,χ70),对比结果如表3 所示.
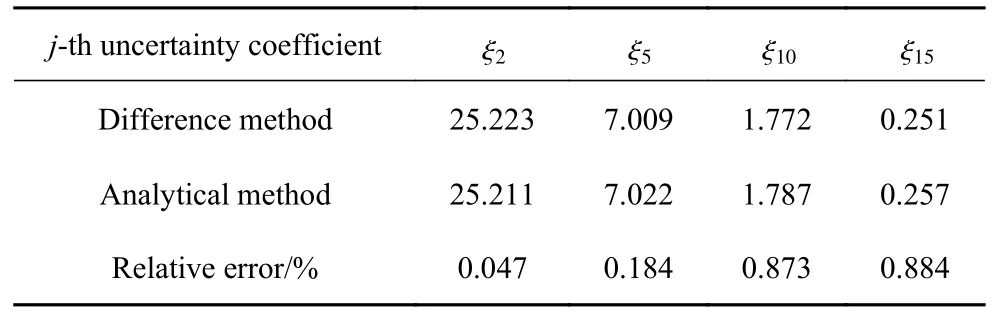
表2 内层优化中不确定系数的灵敏度Table 2 Sensitivity of uncertainty coefficients in inner-loop optimization
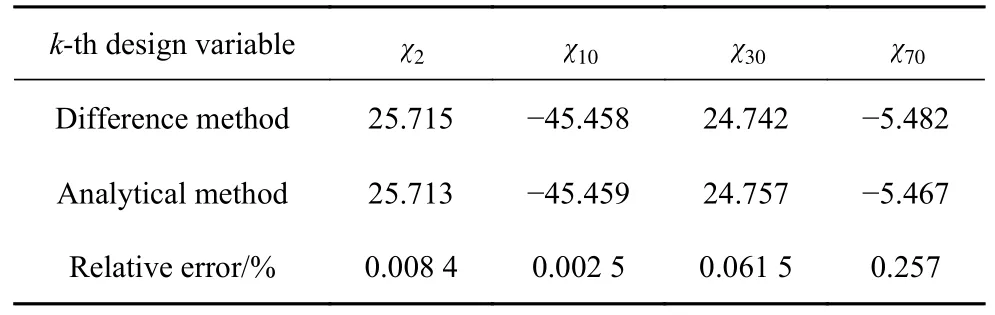
表3 外层优化中设计变量的灵敏度Table 3 Sensitivity of design variables in outer-loop optimization
从表2 和表3 的对比结果中可以看出,第4 节的解析灵敏度和差分法的灵敏度计算结果非常相近,其相对误差均在 1%以内.这证明了本文优化模型及解析灵敏度推导的正确性.
基于本文提出的考虑结构几何不确定性的非概率可靠性拓扑优化模型,本算例中不同工况下的内层优化和外层的优化迭代历史分别如图8,图9 所示.其中,图8 表示第一次的内层优化.从图8 中可以看出,在整个内层优化的过程中,目标函数都能够快速收敛到某一特定值(图8 实线所示),并且结构能够始终满足指定的可靠性指标约束(图8 虚线所示).此外,图9 的外层优化迭代历史也体现了优化模型稳定的收敛性.因此,这也进一步证明了采用梯度优化算法来求解本文提出的非概率可靠性优化模型是合理有效的.
为了进一步验证非概率可靠性拓扑优化结果的合理性,我们将非概率可靠性拓扑优化关心点ξ*(式19)处的几何不确定性(即表示为图7 右列的不确定阈值场)施加到确定性拓扑优化结构(图6 所示)和可靠性拓扑优化结构(图7 左列)上,来进行结构的柔顺性对比,对比结果如表4 所示.以L=80 mm;=1.0的非概率可靠性拓扑优化结构为例(如表4第2,3 列所示),当确定性优化结构中存在几何不确定性时(即关心点 ξ*处的不确定阈值场),结构柔顺性值为C=34.95 N·mm,大于可靠性拓扑优化结构在该关心点 ξ*处的柔顺性值C=33.66 N·mm.此外,其他条件下的非概率可靠性拓扑优化结构同样满足这种情况: (1)L=80 mm,=1.5 时,如表4 第4,5 列所示,C=35.57 N·mm 和C=34.94 N·mm;(2)L=30 mm,=1.0 时,如表4 第6,7 列所示,C=38.78 N·mm 和C=34.87 N·mm.因此,通过上述对比可以看出,当存在几何不确定性时,考虑几何不确定性的非概率可靠性优化结构具有更好的抵抗几何不确定性的能力,即有更小的结构柔顺性.
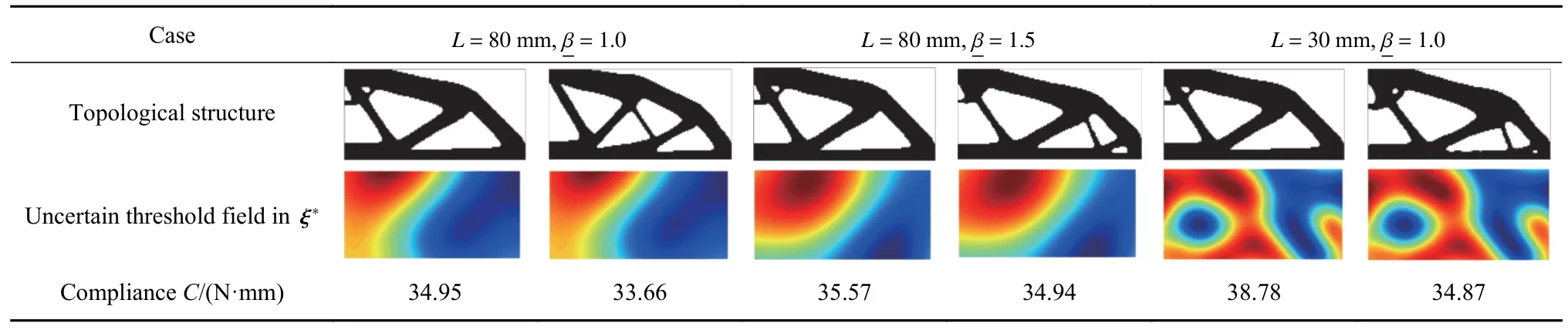
表4 可靠性拓扑优化结构和确定性优化结构在关心点 ξ* 处的柔顺性对比Table 4 Comparison of compliance between reliability-based and deterministic topology optimization structures at concerned point ξ*
5.2 悬臂梁结构的非概率可靠性优化
在本算例中,以悬臂梁结构为例,如图10 所示,悬臂梁结构设计域的尺寸为 1 12 mm×70 mm,离散为 7 840 (112×70) 个单元.悬臂梁结构的左侧完全约束,集中力F=100 N 作用于结构的右下角,方向为-Y方向.不确定阈值场的变化范围为 η(x)∈[0.25,0.75].结构的体积分数约束同样设定为f=50%.本算例考虑了一种不确定阈值场的相关长度L=30 mm 和一种可靠性指标约束值=1.0 来进行考虑几何不确定性的结构非概率可靠性优化设计.
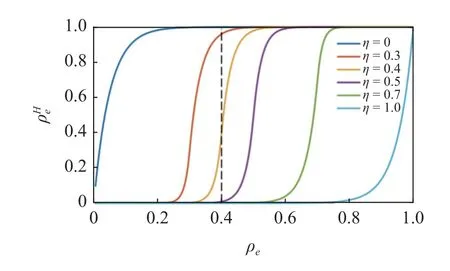
图1 光滑系数 δ=20 时,不同阈值 η 下Heaviside 函数Fig.1 The Heaviside function under different thresholds η when smoothing parameterδ=20

图2 阈值为定值(η (x)≡0.5)及不确定阈值场 η (x) 下的MBB 梁拓扑构型Fig.2 Topological structure of MBB beam considering the constant threshold η (x)≡0.5 and uncertain threshold field
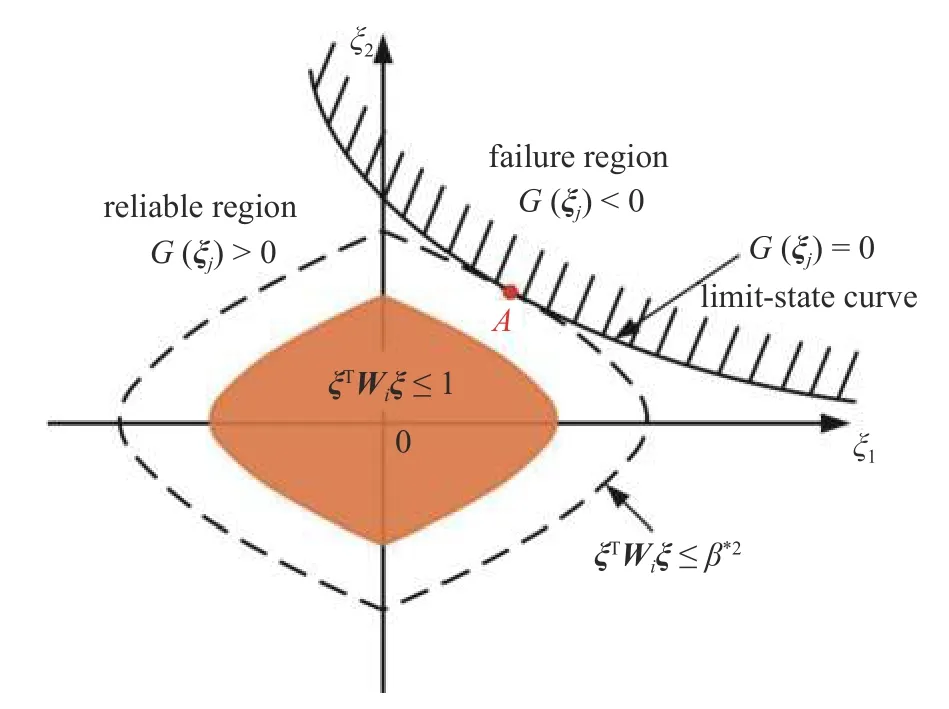
图3 有界场模型非概率可靠性指标示意图Fig.3 Schematic diagram of non-probabilistic reliability index for the bounded field model
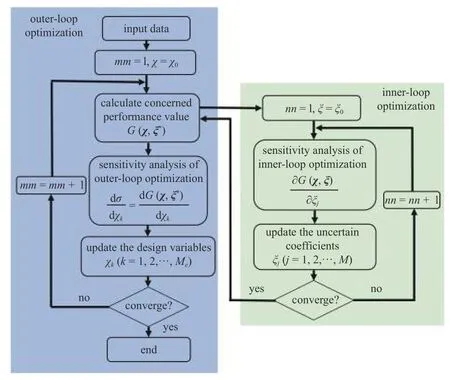
图4 非概率可靠性拓扑优化流程图Fig.4 The flowchart of non-probabilistic reliability-based topology optimization
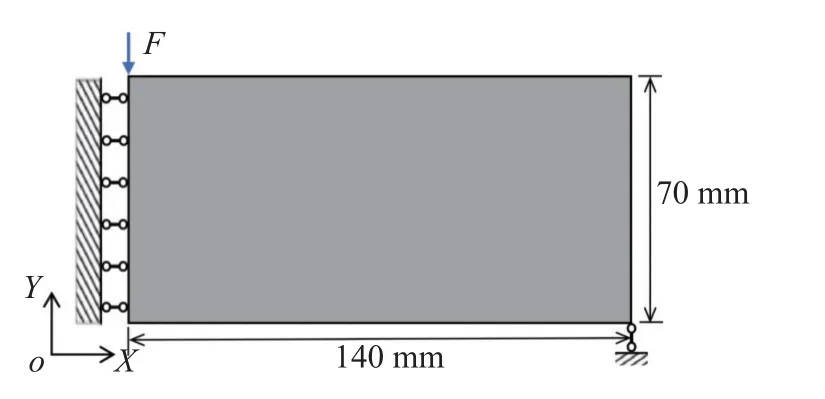
图5 MBB 梁结构设计域Fig.5 Design domain for the MBB beam structure

图6 MBB 梁结构确定性拓扑优化结果(不确定阈值场 η (x)≡0.5),目标函数值C=34.22 N·mmFig.6 Deterministic topology optimization solution for the MBB beam structure (uncertain threshold field η (x)≡0.5) and the objective function valueC=34.22 N·mm
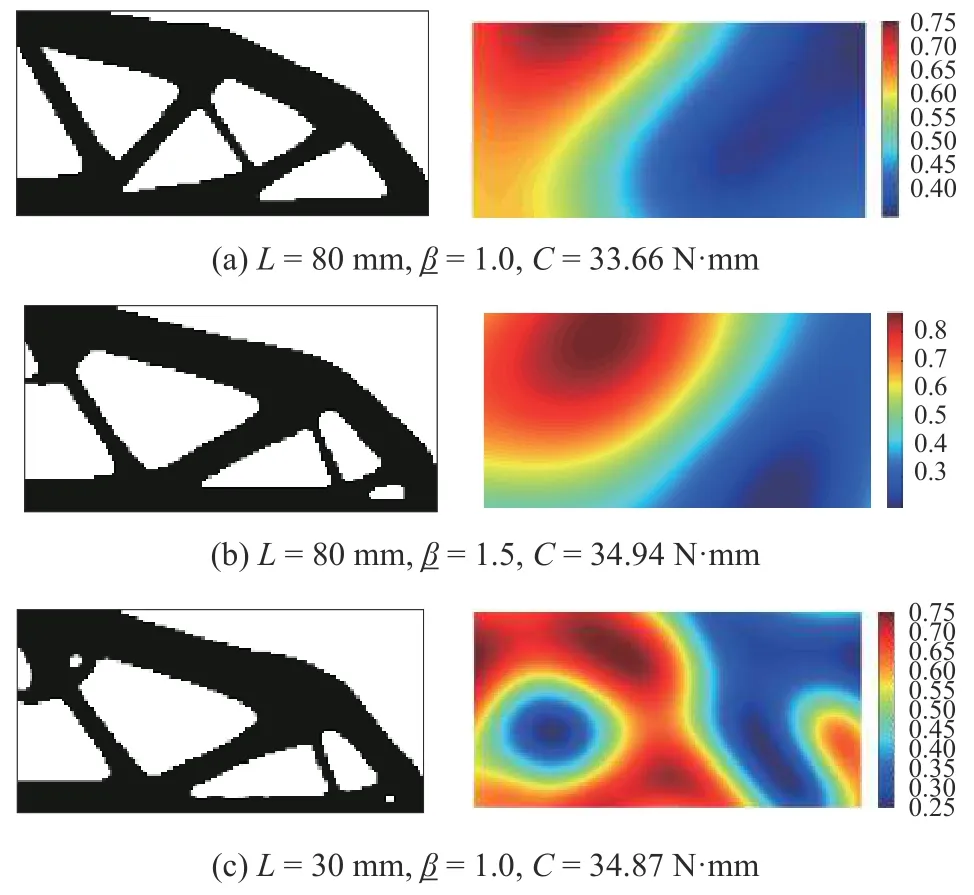
图7 不同相关长度 L 及不同可靠性指标 约束下的非概率可靠性拓扑优化结果(左列)和关心点处的不确定阈值场 η (x) 分布情况(右列)Fig.7 Non-probabilistic reliability-based topology optimization solution (left column) and the distribution of uncertain threshold fields at the concerned point (right column) with different correlation lengthL and non-probability reliability index
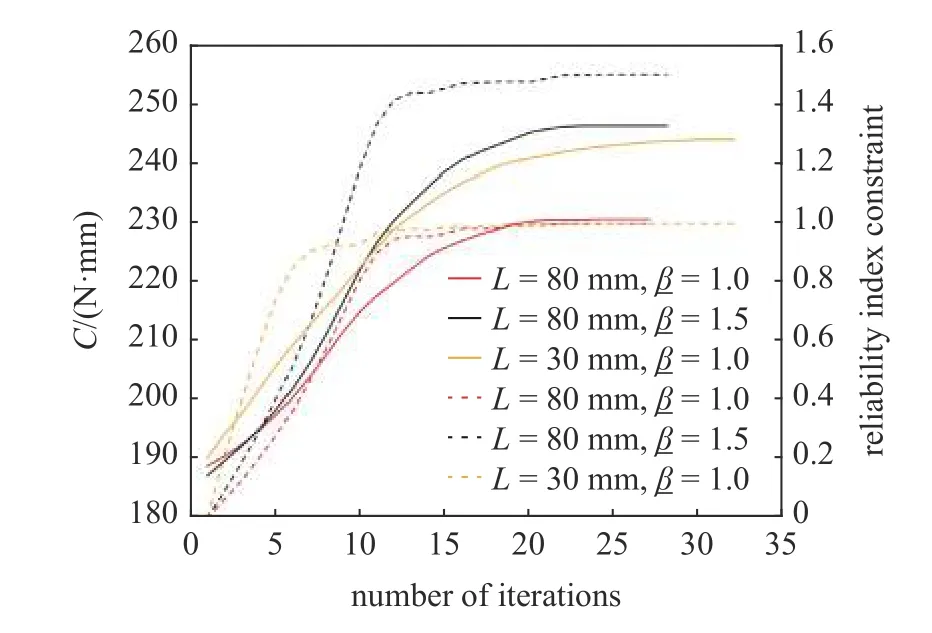
图8 内层优化迭代历史(实线表示目标函数,虚线表示可靠性指标约束)Fig.8 Iteration history of inner-loop optimization (solid lines represent the objective function and dashed lines represent reliability index constraints)
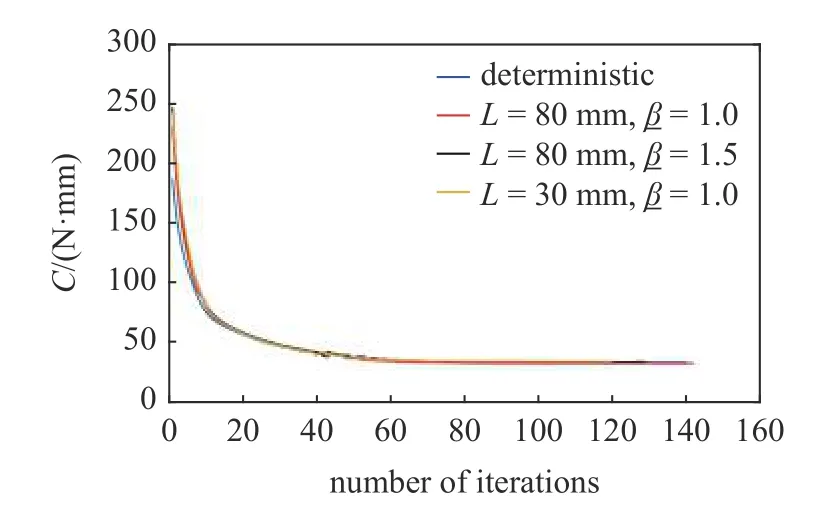
图9 确定性和非概率可靠性拓扑优化的迭代历史Fig.9 Iteration histories of the deterministic and non-probability reliability-based topology optimization
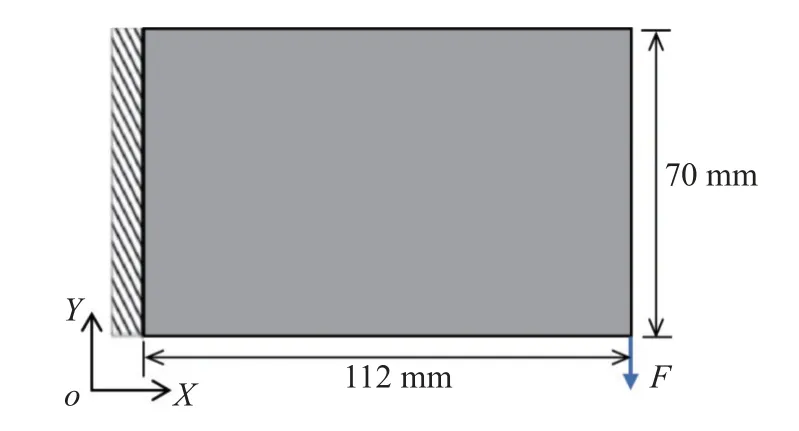
图10 悬臂梁结构设计域Fig.10 Design domain for the cantilever structure
作为对比,本算例中同样进行了悬臂梁结构的确定性拓扑优化设计,在整个优化过程中阈值场在设计域内各点处的阈值均为恒定值,即 η (x)≡0.5,悬臂梁结构的确定性拓扑优化结果如图11 所示.考虑不确定阈值场的结构非概率可靠性拓扑优化结果及关心点对应的不确定阈值场分布情况如图12 所示(L=40 mm,=1.0).对比2 个优化结果可以看出,在材料体积一定的情况下,可靠性优化设计的结构产生了更多的肋来抵抗结构中的几何不确定性,以提高结构的可靠性.本算例进一步证明了本文提出的考虑几何不确定性的非概率可靠性优化模型的有效性.

图11 悬臂梁结构确定性拓扑优化结果(不确定阈值场 η (x)≡0.5),目标函数值C=19.62 N·mmFig.11 Deterministic topology optimization solution for the cantilever structure (uncertain threshold field η (x)≡0.5) and the objective function valueC=19.62 N·mm

图12 相关长度 L=40 mm 及可靠性指标约束值 β=1.0 时的悬臂梁结构非概率可靠性拓扑优化结果和关心点处的阈值场分布,目标函数值C=19.79 N·mmFig.12 Non-probabilistic reliability-based topology optimization solution and the distribution of uncertain threshold fields at the concerned point with correlation length L=40 mm and non-probability reliability index β=1.0 and the objective function valueC=19.79 N·mm
6 结论
本文提出了一种考虑结构几何不确定性的非概率可靠性优化模型,其中结构的几何不确定性通过有界不确定阈值场函数来表示.基于材料场级数展开,不确定阈值场可通过一组不确定系数来描述.优化模型为嵌套优化问题,内层是进行结构的可靠性评估,外层为确定结构的最优布局.本文采用了基于梯度的优化算法来求解该非概率可靠性优化模型.数值算例表明,采用本文提出的非概率可靠性优化方法,可以得到分布更为合理的拓扑构型来提高结构在考虑几何不确定性下的可靠性.

