三维20 节点六面体和10 节点四面体单元的高精度中节点集中质量矩阵1)

侯松阳 王东东 吴振宇 林智炜

(厦门大学土木工程系,福建省滨海土木工程数字仿真重点实验室,福建厦门 361005)

引言

在结构动力分析[1-6]中,质量矩阵的构造形式对有限元计算精度具有显著的影响.其中,常用的有限元质量矩阵构造形式主要包括一致质量矩阵[1,7-8]、高阶质量矩阵[1,9-11]和集中质量矩阵[12-19].其中,集中质量矩阵具有构造形式简单、存储空间小、计算效率高和可与中心差分法等显式积分方案结合使用等优点.而常用的集中质量矩阵构造方法主要包括行求和法[1,13]、节点积分法[14-16]和一致质量矩阵主对角元素放大法(HRZ 法)[17]等.在集中质量矩阵的精度分析方面,Ainsworth 等[16]给出拉格朗日单元采用节点积分方案求解标量波特征值问题时的精度度量理论.Yang 等[18]针对8 节点平面单元提出一种基于数值微分流形的集中质量构造方法.Duczek等[19]研究了Lobatto 单元行求和、节点积分和HRZ 集中质量矩阵之间的等价性.最近,Li 等[20]研究了采用行求和集中质量矩阵时,拉格朗日单元节点布置对频率计算精度和收敛阶次的影响,详细分析了节点均匀分布单元集中质量矩阵的频率精度受限性.

在有限元分析领域,20 节点六面体单元和10 节点四面体单元应用非常广泛[21-25].与27 节点六面体拉格朗日单元相比,20 节点六面体单元不含内部节点,充分利用了单元间的节点共享特性,可显著缩减计算模型的带宽,提高计算效率.与此同时,10 节点四面体单元在复杂形状网格剖分方面具有明显优势.然而,当采用行求和方法构造这两类单元的集中质量矩阵时,主对角线上均出现负质量元素,难以直接用于结构动力分析.目前,最常用的消除集中矩阵负质量元素的有效方法是HRZ 法[17],但是三维情况下该方法缺乏理论层面的精度分析.针对8 节点平面单元的HRZ 集中质量矩阵,Hou 等[26]建立了相应的频率精度表达式,通过分析证明HRZ 集中质量矩阵并不能提供最优的频率计算精度,进一步发展了具有更优精度的8 节点平面单元中节点集中质量矩阵.但是,该研究尚未考虑更为复杂的三维单元.另外,由于中节点集中质量矩阵的角节点质量为0[26],其对时程动力分析的影响也需要进一步厘清.

本文针对三维20 节点六面体和10 节点四面体单元行求和集中质量矩阵出现负质量的问题,提出了三维广义中节点集中质量矩阵的构造形式,并将HRZ 集中质量矩阵作为特例涵盖其中.然后,以20 节点六面体单元为例,构建了三维广义中节点集中质量矩阵的频率计算精度表达式,进而分析了三维HRZ 集中质量矩阵的频率精度.根据三维广义中节点集中质量矩阵的频率精度表达式,通过对其中的待定参数进行优化,构造了20 节点六面体单元的高精度集中质量矩阵.接着,利用中节点集中质量矩阵构造形式简单的特点,将其推广到10 节点四面体单元.最后,对于时程动力分析,通过静力凝聚消除了中节点集中质量矩阵的角节点零质量影响,构造了三维有限元中节点集中质量矩阵的降阶动力计算模型,在保证动力计算精度的同时提高了计算效率.

1 结构动力分析的有限元离散方程

不失一般性,考虑如下的经典波动方程等效积分弱形式[1]

其中,δ 表示变分符号,上标T 代表转置.对于膜或声场问题,场变量u退化为标量u,表示膜的横向位移或声压,外力或源项b退化为标量b.与之对应的梯度矩阵和材料矩阵D分别为

其中,c为波速.对于弹性力学问题,矢量场u={ux,uy,uz}T表示弹性体内一点的位移,b={bx,by,bz}T表示体力,相应的梯度矩阵和材料弹性矩阵D分别为

其中,cp和cs表示压力波和剪力波的波速[11]

其中,λ 和 µ 为拉梅常数,ρ 为材料密度.

其中,NI(ξ) 表示单元第I个节点的形函数,nen为单元节点个数.将式(6)代入式(1)中,可得结构动力分析的有限元离散方程

其中,M和K分别为整体质量矩阵和整体刚度矩阵,f为力向量,可分别由单元质量矩阵Me、刚度矩阵Ke和力向量fe通过组装算子 A 组装得到.Me,Ke和fe的定义为

其中,1 是单位矩阵,对于声场问题,1=1;对于弹性连续体问题,1=diag{1,1,1}.

对于自由振动分析,在式(7)中忽略外力项,并引入如下的简谐波假定

其中,ωh为数值频率,ϕ 为与之对应的振动模态.将式(12)代入式(7),可得自由振动分析的有限元离散方程

2 三维20 节点六面体和10 节点四面体单元的高精度集中质量矩阵构造方法

为表述简洁起见,在下面的讨论中,分别用H20和T10 表示三维20 节点六面体和10 节点四面体单元.

2.1 H20 和T10 单元的HRZ 集中质量矩阵

由于满足变分一致性,式(9)定义的质量矩阵通常被称为一致质量矩阵.当采用行求和法构造集中质量矩阵时,仅需将一致质量矩阵每行的元素累加到主对角元素.因此,对于标量波动问题,考虑规则的H20 和T10 单元构形,例如长方体和直边四面体,其行求和集中质量矩阵分别为

其中,下标 R S 表示行求和法;me为单元的总质量.为清晰起见,图1 和图2 给出了H20 和T10 单元的节点质量分布,其中MNLM (mid-node lumped mass matrix)表示中节点集中质量矩阵.

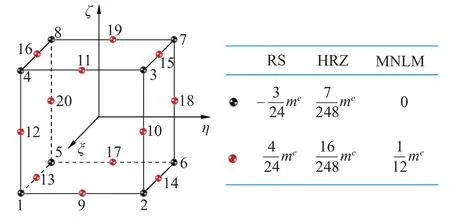
图1 H20 单元3 种集中质量矩阵的节点质量分布示意图Fig.1 Schematic illustration of the nodal mass distribution for three mass lumping schemes of H20 element

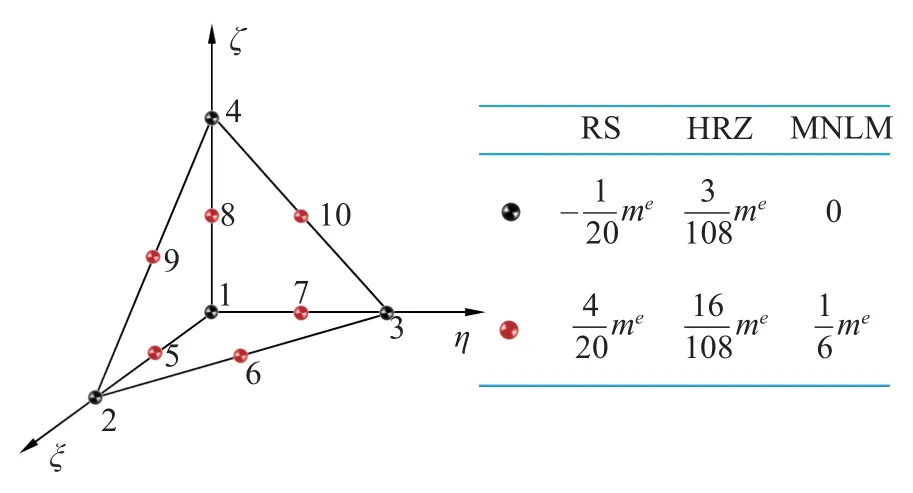
图2 T10 单元3 种集中质量矩阵的节点质量分布示意图Fig.2 Schematic illustration of the nodal mass distribution for three mass lumping schemes of T10 element

由式(14)和式(15)可得,对于H20 和T10 单元,行求和集中质量矩阵中的角节点质量均为负值.根据HRZ 方法,将式(9)中的一致质量矩阵的主对角元素在满足质量守恒的条件下进行比例缩放,即可得到非负的HRZ 集中质量矩阵

其中,r为缩放系数

由式(16) 和式(17),可得H20 和T10 单元的HRZ 集中质量矩阵

图1 和图2 也给出了这两种单元的HRZ 集中质量矩阵节点质量分布情况.

2.2 H20 和T10 单元的非负中节点集中质量矩阵

如前所述,H20 和T10 单元的行求和集中质量矩阵,负质量都出现在角节点上,而中节点则没有负质量问题.因此,可以基于行求和集中质量矩阵中的非负质量元素,通过单元质量守恒将其进行比例放缩,同时将行求和集中质量矩阵中的负对角元素置零,构造一种新型非负集中质量矩阵.该集中质量矩阵的构造流程为

基于式(20)和式(21),H20 和T10 单元的新型集中质量矩阵分别为

由式(22)和式(23)可见,对于H20 和T10 单元,角节点的质量均为零,质量只被分配在中节点上,所以把该集中质量矩阵称之为中节点集中质量矩阵,简称MNLM 集中质量矩阵.同样,图1 和图2 中也描述了H20 和T10 单元的MNLM 集中质量矩阵.

3 H20 单元集中质量矩阵的频率精度分析

本节以H20 单元为例,研究集中质量矩阵构造形式对频率计算精度的影响.为了更全面衡量各类集中质量矩阵的精度,构造如下H20 单元广义集中质量矩阵

其中,α 和 β 是待定参数.为了保证集中质量矩阵的非负性,角节点质量 α 需满足 α ∈[0,1].当 α=7/31 时,式(24)中的广义集中质量矩阵即退化为式(18)的HRZ 集中质量矩阵;而当 α=0 时,即为式(22) 的MNLM 集中质量矩阵.

为了进行频率精度分析,考虑图3 所示的H20单元典型节点影响域.由H20 单元构成的有限元典型节点包括一个角节点xabc和3 个中间节点xa(b+1)c,x(a-1)bc和xab(c+1).θ 和 φ 是与谐波相关的不同方向的入射角,hi为xi方向的单元长度,不同方向的波数ki与k之间的关系满足

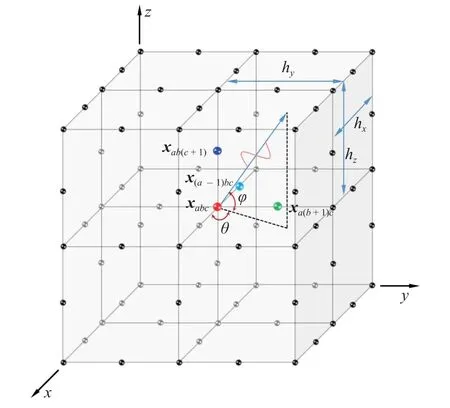
图3 H20 单元典型节点影响域及波动方向示意图Fig.3 Illustration of the typical nodal influence domains and wave propagation angles for a mesh with H20 elements

假设离散节点的波动形式为谐波,4 个典型节点系数可以表示为

方便表述起见,引入算子cos(±lkx±mky±nkz)

当式(28)仅包括两个下标时,有

对于4 个典型节点,将式(26)和式(27)代入式(7),并利用简谐波假定化简可得

其中,AJI=AIJ,KI,J=KIJ为刚度矩阵元素,为了不造成下标混淆,下标的行号和列号之间采用“,”隔开.

由于式(30)有非0 解,则矩阵A的行列式应为0

值得指出的是,式(42)是关于数值频率 ωh的非线性方程,但由于其复杂性,从中直接求解 ωh通常是非常困难的.另一方面,在理论分析中我们关注的是频率误差,而非频率本身,因而可直接引入频率误差e[1]

结合解析频率 ω=kc和式(43),有

将式(44)代入式(42),并忽略e的高次项[26],可得

进一步在式(45)中引入余弦项关于kh的泰勒展开,可得H20 单元广义集中质量矩阵的频率误差表达式

其中h为特征单元长度

将 α=7/31 代入式(48),即得H20 单元HRZ 集中质量矩阵的频率误差表达式

对比式(48)和式(50),可见H20 单元的HRZ集中质量矩阵的精度并非最优.反之,由式(48)可知,α=0 对应的H20 单元集中质量矩阵具有更优的频率计算精度,此时的集中质量矩阵即为MNLM 集中质量矩阵.进一步,将 α=0 代入式(48) 中,即得MNLM 集中质量矩阵的频率误差表达式

基于式(50)和式(51),若忽略频率误差的高阶项,可得三维H20 单元MNLM 集中质量矩阵与HRZ集中质量矩阵两者频率误差之间存在如下关系

4 基于中节点集中质量矩阵的时程分析

对于H20 和T10 单元,式(22)和式(23)表明MNLM集中质量矩阵的角节点质量为0.利用这一特点,可通过静力凝聚建立相应的结构动力分析降阶模型[27],减小整体计算规模,提高计算效率.

将H20 或T10 单元的MNLM 集中质量矩阵代入式(7)的有限元离散运动方程,同时将零质量角节点和非零质量中节点进行分类,可得

其中,下标C和M分别表示单元的角节点和中节点,MMM,KCC和KMM均为正定矩阵.对式(53)中的零质量节点对应的元素,可通过静力凝聚进行模型降阶.将式(53)展开,有

根据式(54),角节点位移向量dC可表示为

将式(56)代入式(55)中,可得仅与中节点有关的有限元离散运动方程

对于结构时程分析,这里采用中心差分法进行时间离散.当采用等时间步长 Δt时,中心差分法第n步的速度和加速度分别为

将式(61)代入式(57),可得第n+1 步的位移更新格式

与此同时,将式(60) 代入式(61),可以得到n=-1步的起步位移向量

5 数值算例

由于本文主要研究不同方法的精度对比,简洁起见且不失一般性,算例均采用无量纲单位.

5.1 长方体空腔问题

首先,考虑齐次边界条件的长方体空腔频率计算问题,长方体空腔的长度、宽度和高度分别为Lx=2,Ly=1 和Lz=1.该问题的频率解析解[28]为

其中,c为波速,本算例中取为1.图4 为该问题采用H20 和T10 两种单元的网格划分情况,其中,H20 单元模型包括216,512 和1000 个单元(1225,2673 和4961 个自由度),T10 单元模型包括1080,2560 和5000 个单元(1981,4401 和8261 个自由度).为了方便对比,图4 有限元模型中,一个H20 单元对应5 个T10 单元.

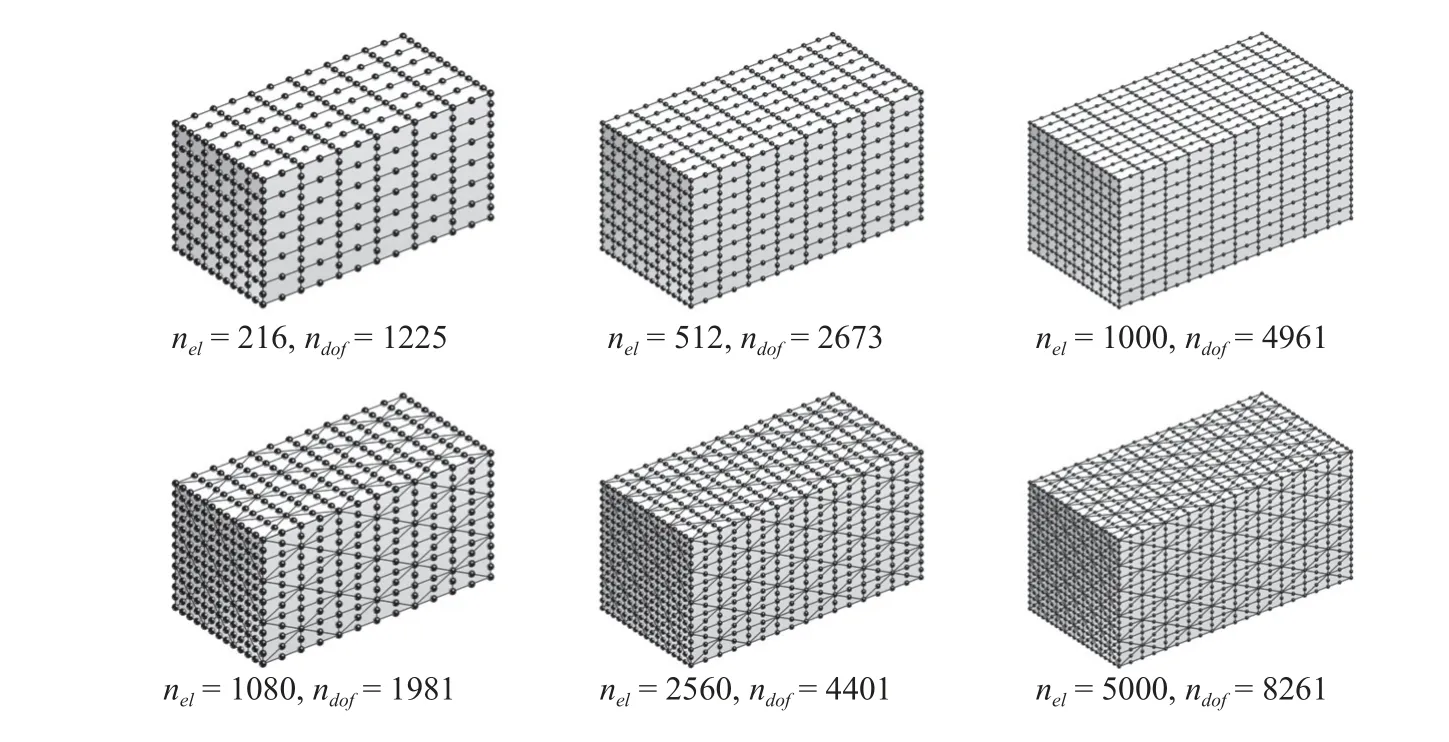
图4 长方体空腔问题有限元网格Fig.4 Finite element meshes of the rectangular cavity problem

图5 和表1 给出了采用图4 系列有限元模型得到的前4 阶频率计算结果.从图5 的频率收敛结果可见,H20 和T10 单元的MNLM 集中质量矩阵的频率计算精度均明显优于HRZ 集中质量矩阵.同时,表1 的频率误差结果对比表明,对于H20 单元,MNLM集中质量矩阵的前4 阶频率计算误差与HRZ 之间比值约为0.66,与式(52)给出的理论结果吻合良好;对于T10 单元,MNLM 集中质量矩阵与HRZ 集中质量矩阵相比的频率误差比值小于0.40,精度优势更为显著.另外,值得指出的是,无论是HRZ 还是MLNM 集中质量矩阵,在相同自由度数条件下,T10单元的频率计算精度均优于H20 单元.

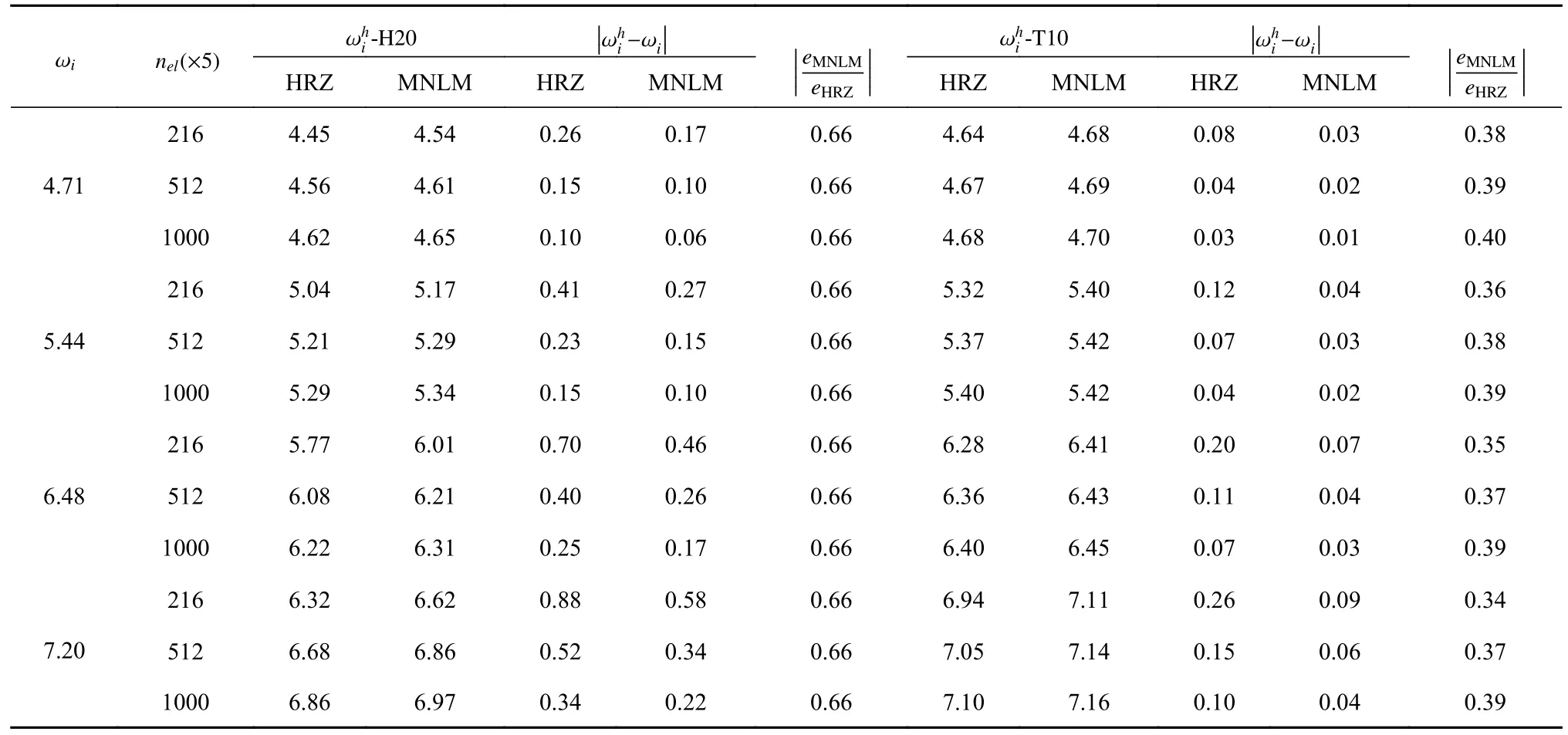
表1 长方体空腔问题前四阶频率计算精度对比Table 1 Accuracy comparison of the first four frequencies for the rectangular cavity problem

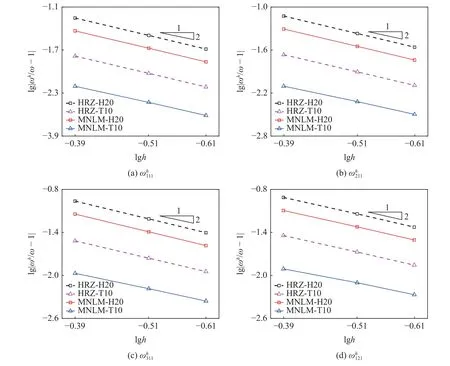
图5 长方体空腔问题前四阶频率收敛特性对比Fig.5 Convergence comparison of the first four frequencies for the rectangular cavity problem

5.2 弹性力学长方体问题

第2 个算例是弹性力学长方体问题.该模型的几何尺寸与长方体空腔问题一致,材料弹性拉梅常数 λ=15/26,µ=5/13.边界条件如图6 所 示: 在x={0,Lx}处uy=uz=0,在y={0,Ly} 处ux=uz=0,在z={0,Lz} 处ux=uy=0.根据文献[29],可导出该模型的压力波和剪力波频率解析解分别为

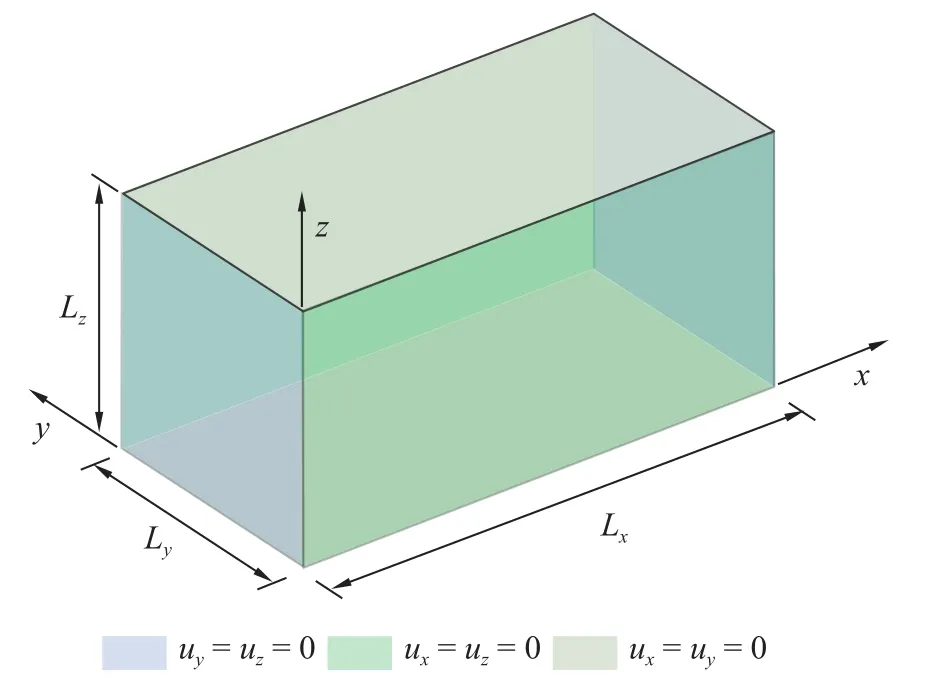
图6 长方体弹性连续体模型Fig.6 Description of the rectangular elastic continuum problem

其中,对于压力波频率,下标需满足l,m,n≥1;对于剪力波频率,下标需满足至少有两个大于等于1.值得需要注意的是,下标均大于等于1 时,剪力波频率为二重根.

在对该结构进行自由振动分析时,同样采用图4的有限元网格进行计算.前6 阶频率的收敛对比结果见图7.可见,H20 和T10 单元的MNLM 集中质量矩阵的频率计算精度均明显优于HRZ,验证了所提方法在弹性力学问题中同样具有良好的适用性.

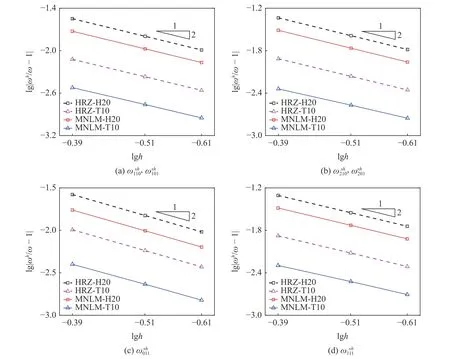
图7 长方体弹性体前六阶频率收敛特性对比Fig.7 Convergence comparison of the first six frequencies for the rectangular elastic continuum problem

为了深入验证所提集中质量矩阵的动力性能,进一步计算该弹性力学问题的时程响应.计算中考虑如下的位移解析解

其中,取t=0 即可得到有限元动力分析的初始位移和初始速度.

有限元分析中H20 和T10 单元分别采用图4中的1000 个单元和5000 个单元进行时程分析,时间步长统一取 Δt=0.01.图8 给出了t=10 时刻的各方向位移误差云图,结果表明H20 和T10 单元的MNLM 集中质量矩阵的位移计算精度均优于对应的HRZ 集中质量矩阵.此外,图9 给出了归一化计算时间[30]对比结果.相比HRZ 集中质量矩阵,H20单元的MNLM 集中质量矩阵的计算效率提升了约4.3 倍,T10 单元的MNLM 集中质量矩阵的计算效率提升了约3.0 倍.由此可得,MNLM 集中质量矩阵不仅可以显著提高计算精度,而且在进行时程分析时,与结构动力分析降阶模型相结合可以提高计算效率.

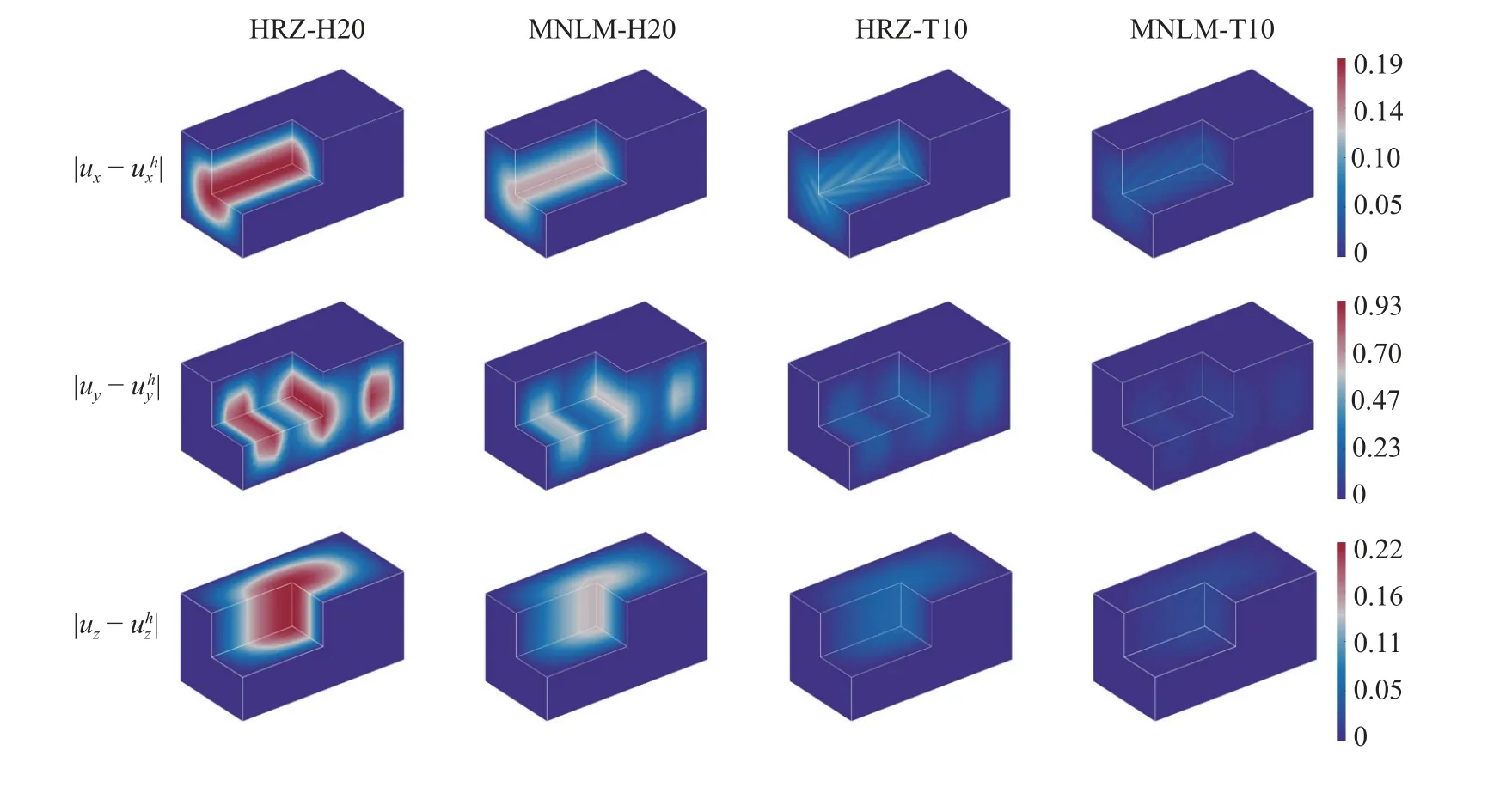
图8 长方体弹性体 t=10 时刻的位移误差云图Fig.8 Displacement error contour plots for the rectangular elastic continuum problem att=10

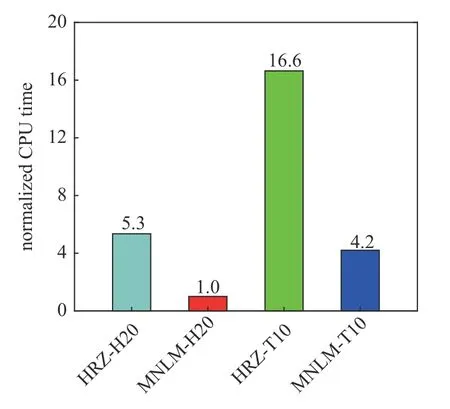
图9 长方体弹性体时程分析效率对比Fig.9 Efficiency comparison of the transient analysis for the rectangular elastic continuum problem

5.3 1/4 圆筒空腔问题

最后一个算例是图10 所示的1/4 圆筒空腔问题.该模型的内径ri=1,外径ro=2,高度H=1,波速c=1.当采用齐次边界条件时,该问题的频率解析解为

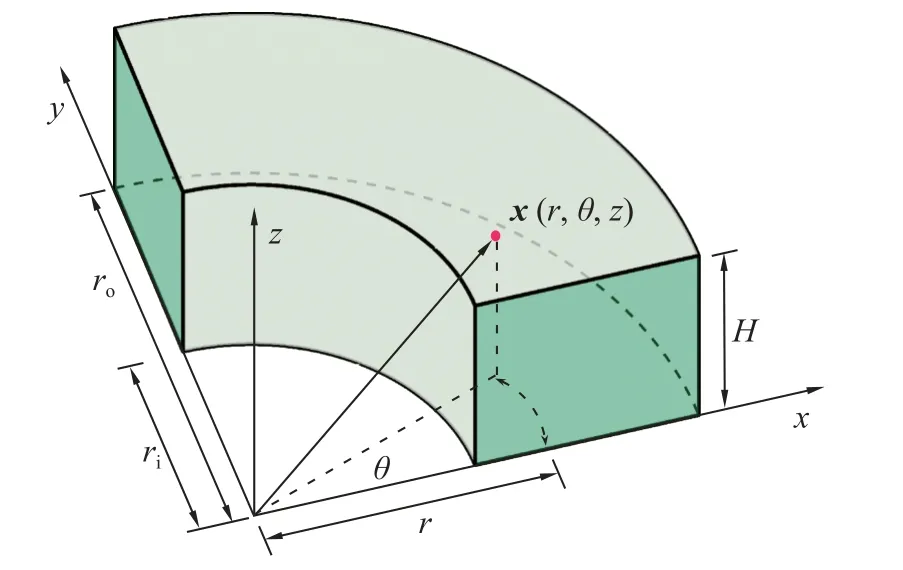
图10 1/4 圆筒空腔问题Fig.10 Description of the quarter-cylinder cavity problem

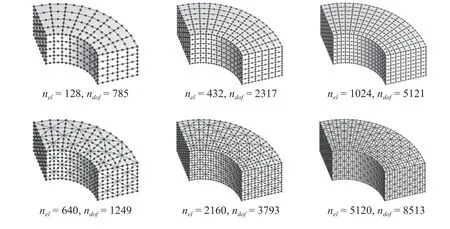
图11 1/4 圆筒空腔问题有限元网格Fig.11 Finite element meshes of the quarter-cylinder cavity problem

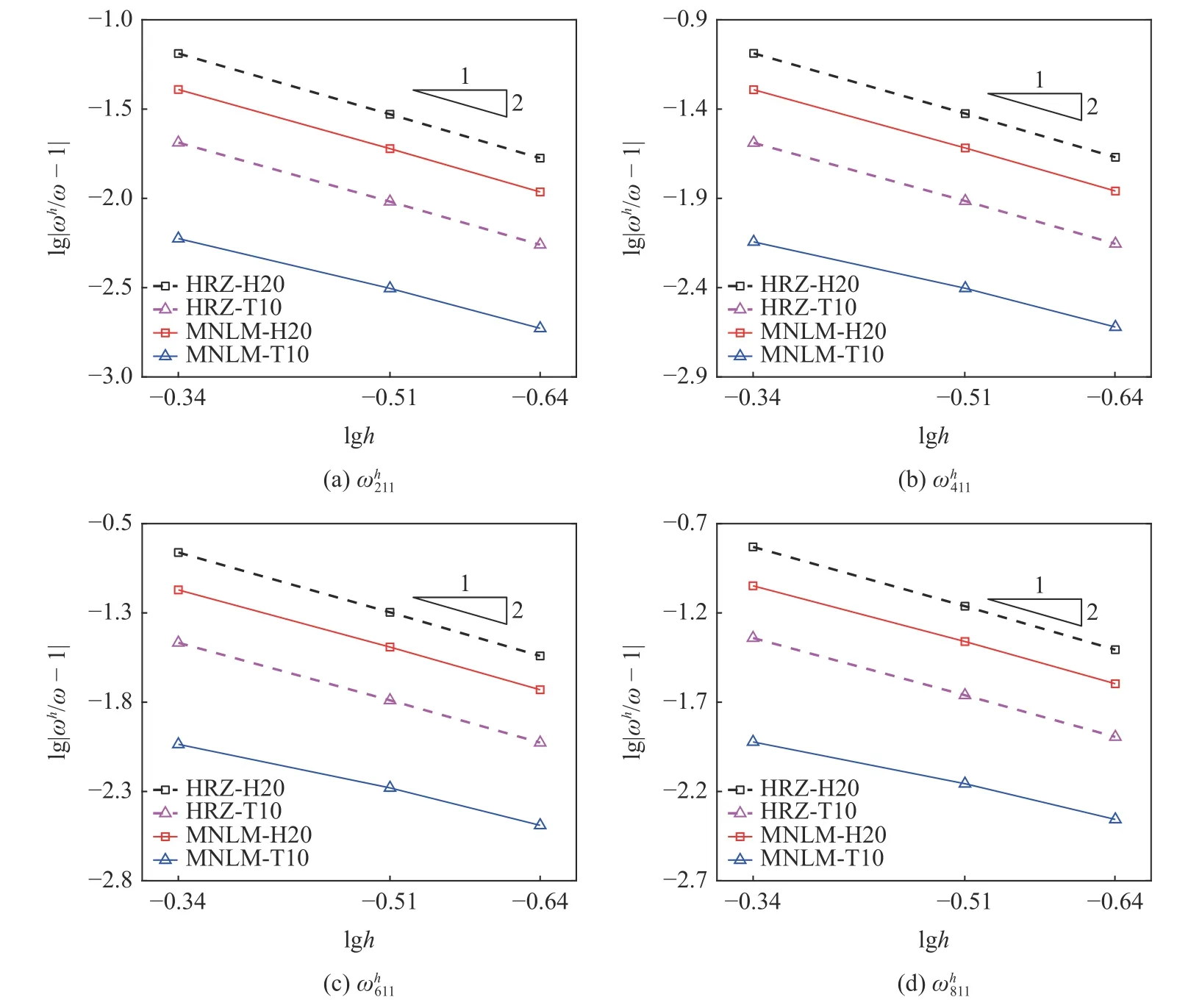
图12 1/4 圆筒空腔问题前四阶频率收敛特性对比Fig.12 Convergence comparison of the first four frequencies for the quarter-cylinder cavity problem

对于该问题,我们同样进行时程分析,其中考虑的空腔内解析声压解为

有限元分析的初始条件可通过在式(70) 中令t=0 给出.同样,式(11)中源项b也可由式(70)求得

在时程分析中,有限元模型采用图11 中的1024 个H20 单元和5120 个T10 单元,时间步长为Δt=0.01.图13 给出了x=(1.5,π/4,0.5) 处的声压数值解uh的时程曲线及误差对比结果,图14 给出了t=12时刻的位移误差云图.结果显示,对于时程分析,H20 和T10 单元的MNLM 集中质量矩阵的计算精度同样优于对应的HRZ 集中质量矩阵.

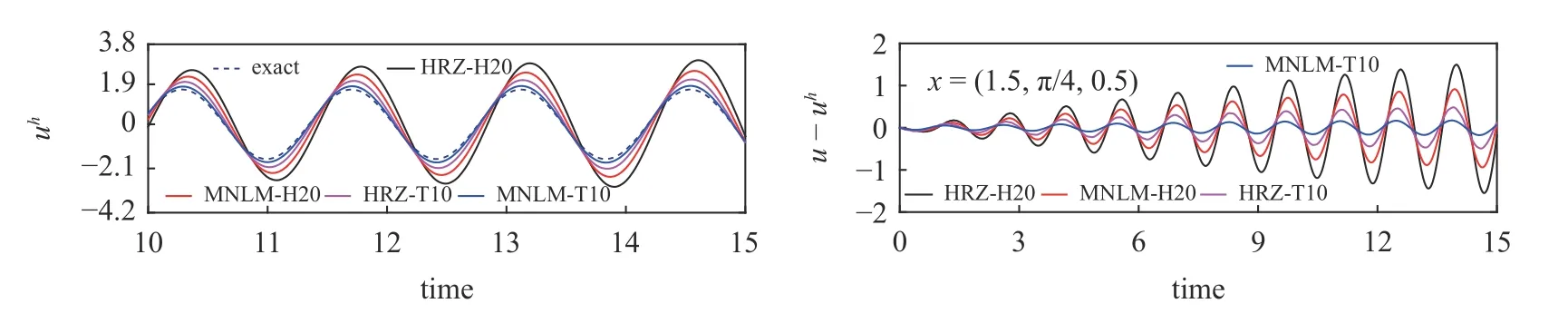
图13 1/4 圆筒空腔问题声压时程对比Fig.13 Comparison of the acoustic pressure time history for the quarter-cylinder cavity problem

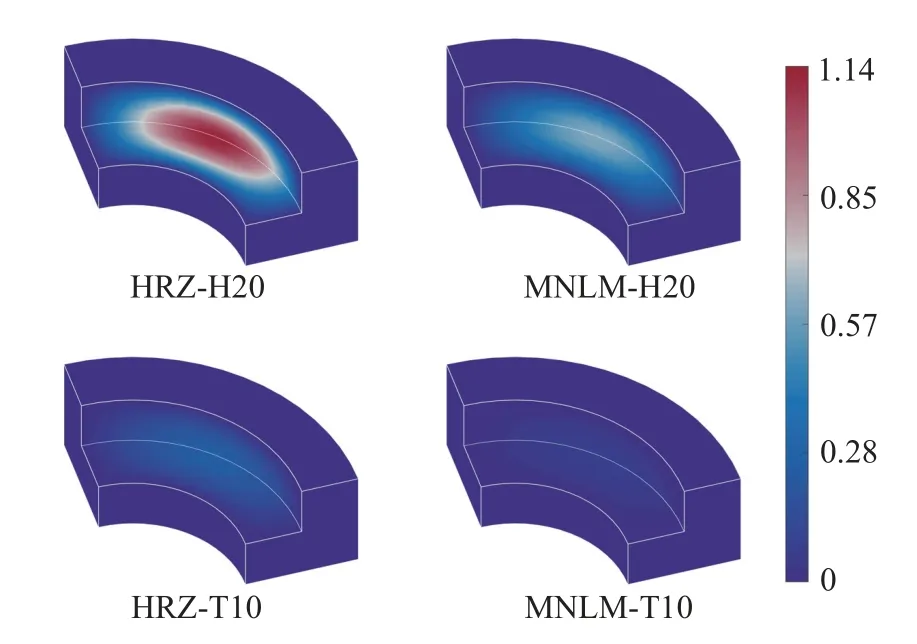
图14 1/4 圆筒空腔问题 t=12 时刻的声压误差云图Fig.14 Acoustic pressure error contour plots for the quarter-cylinder cavity problem att=12

与此同时,图15 给出了MNLM 和HRZ 集中质量矩阵的计算效率对比.该问题的计算效率结果再次表明,对于具有非均匀网格特征的1/4 圆筒空腔问题,相较于HRZ 集中质量矩阵,H20 和T10 单元的MNLM 集中质量矩阵的计算效率分别提升了约1.3 倍和3.0 倍,实现了计算效率的显著提升.

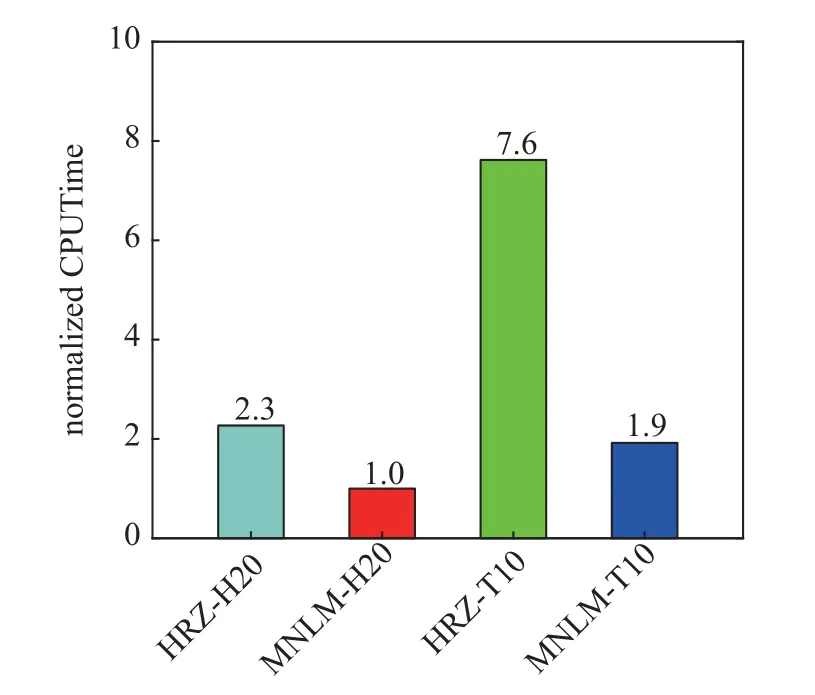
图15 1/4 圆筒空腔时程分析效率对比Fig.15 Efficiency comparison of the transient analysis for the quartercylinder cavity problem

6 结论

本文针对结构分析中应用广泛的三维20 节点六面体单元和10 节点四面体单元,系统研究了其集中质量矩阵构造方法和精度.通过引用一种包含待定参数的三维20 节点六面体单元广义集中质量矩阵,建立了相应的频率精度表达式,进而揭示了不同集中质量矩阵的理论精度.研究表明,对角元素比例缩放法,即HRZ 方法,作为所提广义集中质量矩阵构造方法的一个特例,虽然能够保证集中质量矩阵元素非负性,但其精度并非最优.随后,通过对广义集中质量矩阵频率精度进行优化,提出了一种精度更优的三维20 节点六面体单元中节点集中质量矩阵构造方法,并将其推广到10 节点四面体单元.中节点集中质量矩阵同样具有非负特性,但角节点的质量为零,可以方便地进行模型降阶.典型算例的频率和时程计算结果均表明,与HRZ 集中质量矩阵相比,三维20 节点六面体单元和10 节点四面体单元的中节点集中质量矩阵在计算精度和效率方面都得到了显著提升.以20 节点六面体单元为例,就精度而言,如表1 所示,中节点集中质量矩阵的频率计算误差比HRZ 集中质量矩阵降低了约1/3;就效率而言,如图9 和图15 所示,对于弹性力学问题和势问题,中节点集中质量矩阵的时程分析计算效率约为HRZ 集中质量矩阵的5 倍和2 倍.