基于自适应稀疏多项式混沌的流场/声爆多源不确定量化技术研究1)

赵 欢 黄宇君 邢浩楠

*(西北工业大学航空学院,西安 710072)

†(中山大学航空航天学院,广州 510275)

引言

新一代环保型超音速民机的流场/声爆特性受多源不确定性影响,如飞行状态和外形不确定导致气动性能产生变化,大气参数不确定使感受音强水平预测不准等,造成了设计的飞行器性能表现非常敏感,可能并不是最佳状态,有可能急剧变差甚至失效,导致经济成本增加以及任务失败等[1-4].

在基于高可信度流场/声爆的数值分析过程中,面临的不确定源主要包括边界/初始条件、湍流模型假设/参数取值、网格/误差、湍流度等造成的数值模拟不确定性[5-6];加工误差/腐蚀、损伤、变形等几何不确定性[7];飞行状态/大气环境等工作条件不确定性[8-9]等.NASA 兰利研究中心在白皮书[10]中指出,在气动外形、结构以及控制系统设计过程中,考虑各种可能不确定性的影响是非常重要和有意义的(包括参数与模型不确定性),并且随着计算能力的提高、各种先进的不确定量化与设计方法的发展,考虑不确定性的飞行器分析和设计方法将会提供更加稳健和可靠的设计方案.德国联邦经济与劳动部也专门成立了国家项目 (Management and Minimization of Uncertainties in Numerical Aerodynamics,MUNA)[11],专门识别和量化气动计算分析中的不确定性,并建立了考虑不确定性影响的稳健气动优化设计方法.NASA 在CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences[12]中明确提出了对先进多学科不确定性量化技术的迫切需求,并多次组织了多学科不确定量化挑战研讨会[13].近些年来,随着飞机设计水平和竞争压力的不断提高,经济、绿色以及低风险的飞行器占据着巨大优势,而考虑多源不确定性的气动/声爆多学科分析方法将为这类飞行器设计满足严苛的设计指标提供最有竞争力的设计手段[14-15].

多学科多源不确定量化 (uncertainty quantification,UQ)指通过有效的分析手段定量估计各学科系统中多种不确定源对各个学科性能表现的影响,这个过程通常可以规则化为一个多维变量积分与数值分析的问题.然而工程问题通常是非常复杂和计算昂贵的,比如高可信度CFD 数值模拟和高可信度声爆分析系统,以至于通过经典的数值分析手段去获得解析解是不可能的,也是难以承担的.目前,UQ 方法主要包括嵌入式方法和非嵌入式方法两类.其中嵌入式UQ 方法指通过在原分析系统或模型中嵌入包含待定系数的随机模型,然后通过数次求解修改后的系统获得对随机模型的解[5].早期研究人员通过将包含待定系数的随机代理模型如多项式混沌展开(polynomial chaos expansion,PCE)、随机配置(stochastic collocation,SC)和Karhunen-Loeve (KL)等模型嵌入到CFD 数值模拟系统中,再通过数次求解修改后的系统获得随机代理模型的确定表达,从而估计出系统的不确定性量化指标[5],但因为要对原始系统进行修改而带来了额外工作,使用门槛增加.相反,非嵌入式UQ 方法仅仅将原系统或模型当做黑箱处理而进行多次模拟求解,从而免去了修改原系统带来的麻烦,操作门槛非常低.

近些年来,非嵌入式方法由于仅需要对原始系统进行多次求解带来的便捷性从而获得了更加广泛的关注和应用.本文主要聚焦非嵌入式UQ 方法.一些研究者已经总结了当前不确定量化方法在CFD模拟[6,16-17]和声爆分析[2,18-19]以及考虑不确定性的气动稳健优化设计[1,7,20-21]和多学科稳健优化设计[22]中的应用情况.

随着非嵌入式UQ 方法在气动/声爆UQ 中得到了越来越广泛的应用,其效率、收敛性、稳定性和可靠性成为使用者关注的重点.当然,UQ 方法的表现也与特定的UQ 问题息息相关,包括不确定变量数量、不确定变量分布类型、系统的复杂性、以及多学科性能表现对不确定量化准确性的影响等许多因素.虽然一些流行的UQ 方法在CFD 分析问题中得到了广泛应用,但在针对具体气动布局时,需要设计者在效率和准确性上折衷选择.本文主要讨论对输入不确定变量概率分布已知的应用进行UQ 的问题,并假设构建不确定变量概率分布所需信息是充足的.对概率类型的不确定变量,其统计矩估计如下所示

目前非嵌入式UQ 方法主要包括4 类最主流的方法,即基于抽样的方法、数值积分方法、随机代理模型方法以及基于Taylor 展开的方法等.其中,基于抽样的方法具有最广泛的适应性和与维数无关的特点,但通常花费非常高,如蒙特卡洛模拟(Monte Carlo simulation,MCS)抽样方法;数值积分方法适用于较少变量和积分收敛的问题;基于Taylor 展开的方法则在输入变量小范围变化时收敛性良好;而随机代理模型方法对于平方可积且分布规则的系统保持二阶收敛性和稳定性.因此,针对不同系统的UQ 问题应该选择最合适的方法.这4 种方法的特点总结对比如表1 所示.

表1 考虑多源不确定性的不确定量化方法总结Table 1 Uncertainty quantification methods considering multi-source uncertainties

对于气动分析问题,由于压缩性和黏性的影响,气动表现通常是非线性或强非线性的,并且随着要考虑的不确定变量增多(例如飞行状态以及外形加工误差等多源不确定),使得除了PCE 方法以外的其余3 种方法都不同程度地遭遇高昂计算花费的难题,并且目前难以通过有效的办法解决[1,23-24].而PCE 方法虽然具有良好的特性,但快速构建准确的PCE 近似仍然是当前国际研究的热点和难点.

因此,针对气动/声爆多源不确定性量化对传统气动不确定量化方法带来的巨大挑战,本文提出了一种基于全自适应前向-后向选择(fully adaptive forward-backward selection,FAFBS)的高效稀疏多项式混沌(PC)重构方法,突破了传统不确定量化方法适用范围窄或花费巨大的难题,以适用于更加复杂的流场/声爆不确定量化问题.本文主要安排如下:第1 节提出了基于FAFBS 的高效稀疏PCE 重构方法,并建立了适用于多源不确定变量的高效UQ 方法.第2 节使用发展的基于FAFBS 稀疏PC 方法、国际流行的基于正交匹配追踪(orthogonal matching pursuit,OMP) 或者最小角回归(least angle regression,LAR)的稀疏PC 方法以及全PC 方法分别对4 维Park 函数、跨音速RAE2822 翼型流场和标准声爆算例进行UQ 的对比研究,成功验证了发展的基于FAFBS 的PC 方法相对于另外两种方法的巨大优势,可完全满足高效飞行器复杂流场/声爆多源不确定量化以及气动稳健优化设计需要.第3 节对本文的结果进行了总结.附录中对高可信度跨音速翼型流场数值模拟精度和标准声爆算例精度进行了验证,表明本文使用的数值计算方法的可靠性.

1 高效的稀疏多项式混沌重构方法

1.1 多项式混沌方法

假设定义在概率空间 (Ω,Θ,P) 的实随机变量或随机过程f∈L2(Ω),即f:Ω →R,则f可以表达为

其中 Γk表示阶数为k(k=0,1,2,···) 的多项式,系数a(·)为实数.=(ξ1,ξ2,···ξd) 代表相互独立的随机变量输入集合.对于非独立的随机变量,可通过Rosenblatt转换将其转换为独立随机变量[25].此外,也可通过改变PCE 重构策略或者使用基于数据的任意多项式混沌(arbitrary polynomial chaos,aPC)构建方法使之能用于任意分布和相关的随机变量[26].进一步,上述式子可以简写为

其中 αk和 ψk与式(2)中的a(·)和 Γk一一对应.多项式Γk类型的选择应该和输入随机变量分布的类型相对应,以保证PCE 近似的快速收敛性.Cameron 等[27]证明了Wiener-Hermite 类型多项式能保证对任何平方可积的高斯类型输入函数的收敛性.Xiu 等[5]将原来仅针对高斯类型输入PC 推广到包含更多类型的输入分布,针对每个输入分布类型采用不同类型多项式,即Wiener-Askey PCE 或者广义PCE (generalized PCE,GPCE),并证明了Wiener-Askey PCE 使用相应的多项式类型和输入类型能保证至少二阶收敛性.值得注意的是,对于Hermite 多项式以及对应的Gaussian 分布类型,为提高收敛性和准确性通常要求输入为标准正态分布.因此,对于一般分布而言,本文可以通过变换公式将其转换为标准正态分布[25].

每个多维多项式基函数可以通过单变量基函数张量化得到,即

其中ki为多项式阶数 (ki=0,1,2,···,∞).对于阶数为p(p=0,1,2,···,∞)的多变量基函数满足

其中k=(k1,k2,···,kd) 代表 ψk在各个维度的阶数.当式(2)在阶数p被截断,f可以表达为

其中Mp代表了截断后保留的多项式项数,ε (Ξ) 为截断误差.

PCE 重构可分为嵌入式和非嵌入式两种途径.嵌入式PCE (IPCE)通过将PCE 方程带入到物理模型方程(如N-S 方程)内代替某个变量,然后通过修改物理模型求解程序,例如CFD/声爆分析程序,然后通过数次的求解就可以得到所有的PCE 系数.非嵌入式PCE (NIPCE)把求解程序如CFD/声爆分析程序等当做黑箱处理,通过对输入变量抽样,数次调用确定性的CFD/声爆分析程序求解器获得要近似的输出响应,然后利用非嵌入式PC 重构途径求出PCE 系数,即得到近似CFD/声爆分析程序的PCE近似.本文主要使用基于配点法(也叫做最小二乘法)的NIPCE 进行不确定性量化研究,基于最小二乘的NIPCE 解决如下最小化问题[28-29]

其中 α=(α1,α2,···,αMp)T代表系数估计向量,N≥M应该被满足以至于获得唯一的最小二乘解.测量矩阵 Ψ 被定义为

1.2 基于全自适应前向-后向选择的稀疏多项式混沌重构技术

然而上述传统基于最小二乘的NIPCE 使用经典格式截断后,截断项数随空间维数和展开阶数增加而呈几何级数地增加,从而导致所需的样本数急剧增多,近似精度也难以得到保证,即“维数灾难”难题,如图1 所示.尤其对于气动问题而言,PCE 近似的计算花费随流场分析精度增加剧烈增加,并对于包含转捩、激波和分离等复杂流动要求更高的截断阶数,从而加剧了“维数灾难”难题.

图1 PCE 项数随维数和阶数的变化(采用HS 截断格式,q=1)Fig.1 PCE terms varying with the dimension and order (using HS truncation scheme,q=1)

针对这一问题,基于 ℓ1-最小化的稀疏多项式混沌重构方法已经被广泛发展,并对于高维和高阶PCE 问题展示出了极大的优势[30].基于BPDN (basis pursuit denoising)的 ℓ1-最小化公式为

其中 β=(β1,β2,β3,···) 的1 范数定义为其所有元素的绝对值之和,即 ‖β‖1=|β1|+|β2|+|β3|+···.因为解决式(10)所示的优化问题有许多思路,也就有各种不同的稀疏PCE 重构方法[28].比如当前最流行的OMP 以及LAR 等算法.其中,OMP 是典型的前向选择算法,从空活跃集开始,OMP每一步选择与当前残差向量(初始残差向量为输出向量)相关性最大的基向量并增加到活跃集,然后更新预测系数和残差,直到满足停止条件.值得注意的是,OMP 是相对更快的一种稀疏性重构算法,但由于大的贪婪性,其稀疏性通常小于 ℓ1-最小化解集.相较于OMP,LAR 算法有更少的贪婪性,是一种经典的LASSO 算法[31].最小角回归用于稀疏PCE 重构过程如下.

(2) 初始化所有候选多项式系数为0,即α1=α2=···=αMp=0.并设置初始残差向量 γ=Y.初始活跃集集合为空集.

(3) 从候选基向量集合中找出与当前残差向量最相关的基向量 ψi,并添加 ψi到活跃集.

(4) 根据当前残差和活跃集元素使用最小二乘方法估算当前恢复系数,移动 αi从0 到直到存在其他的基向量 ψj(j≠i,ψj∈Σ′) 和当前残差有更多相关性超过 ψi.更新 αi并增加 ψj到当前活跃集.

(5) 根据当前残差和活跃集元素使用最小二乘方法估算当前恢复系数和,同时移动 { αi,αj} 在{,}定义的方向(即等角方向)直到存在其他的基向量 ψk(k≠i,j,ψk∈Σ′) 和当前残差有更多相关性超过 { ψi,ψj}.

重复这个过程,直到当前残差满足停止标准或者m=min(M,N-1) 个基向量已经被选择.OMP 和LAR 都是逐步的前向选择算法,通过这个过程,他们不断地选择相关的基函数进入活跃基集合.OMP 每步更新系数是通过一般的最小二乘途径,而LAR 选择了更少贪婪性的系数更新策略,直到LAR 最后一步更新系数通过一般最小二乘途径(N≥Mp).然而,这两种方法选择的重要PC 基以及恢复的PC 系数仅仅依靠观测样本,以至于修建的PCE 模型是否是全局最优需要通过交叉验证完成.

目前,大多数 ℓ1-最小化算法均是前向选择算法,如OMP 和LAR,即每次选择一个重要的基函数到活跃基集合并更新多项式系数,直到达到停止标准.这个过程中,前向选择算法通过拟合不断增多的基函数以减小近似误差.一些文献指出[32-33],ℓ1-最小化算法通过最小化 β1,如式(10)所示,并不是直接控制解向量 β 的稀疏性.因此,它得到的是一个亚最优的近似解,也使得这个稀疏重构过程更加复杂和缺少稳定性.为了获得更加稀疏的多项式混沌代理模型,作者前期提出了一种全新的自适应前向-后向选择(adaptive forward-backward selection,AFBS)算法用于稀疏多项式混沌重构[28].该方法充分结合了前向选择和后向消除算法的优势,使稀疏多项式混沌重构过程高效稳定地被执行.

该算法的具体过程可参考作者前期工作[28,30].该算法首先通过OMP 算法执行前向选择步,在选择了至少两个重要的基向量到当前活跃基后,后向选择步自动被执行.后向选择步将检查当前活跃集中所有入选的基向量,找出冗余的或不重要的一个并剔除.在后向选择-剔除步里,算法执行了一个迭代循环,即每次选择一个冗余的基向量,然后判断能否剔除,直至满足停止条件.

然而在后向选择步选择了可能冗余的基向量之后,本文需要判断: 剔除这些变量的累积平方损失是否已经可以忽略.为此,本文定义了一个阈值参数v1,当d-＞v1d+时,则可以剔除,否则不能剔除.其中d+代表了前向选择步中平方损失的累积变化,d-代表了在后向选择步中平方损失的累积变化.在所有基函数被遍历后或者截断误差被满足后,则自适应前向-后向选择迭代过程会停止,进入后向检查步.这个后向检查步同前一个后向选择-剔除步基本算法规则一样,其目的是再一次筛选所有进入活跃集中的基向量,找出冗余的或不重要的并删除它们.在这个过程里,本文引入了另外一个阀值参数v2以判断是否满足剔除条件.v2的定义同v1类似,即剔除选择的冗余基函数后是否会引起累积最小平方损失的显著减少,如果是,则剔除,否则不剔除.在作者提出的原始AFBS 算法中,这两个参数v1和v2的值需要设计者根据经验合理给出,不合理的阈值可能会造成拟合误差难以满足要求或者样本需求量变大.

因此,为了彻底解决这个问题对AFBS 算法的困扰,本文提出了一种新的FAFBS 算法去构建基于试验样本的最优PC 代理模型.该算法在原始AFBS 算法的基础上,使用加强学习粒子群优化(comprehensive learning particle swarm optimizer,CLPSO)[34]算法寻找使基于AFBS 构建的PC 代理模型交叉验证误差最小的阈值参数v1和v2,然后执行最优的AFBS 算法建立PC 模型.因为AFBS 算法是非常高效的,这个过程也不会消耗更多时间.CLPSO 改进了标准粒子群算法的早熟问题,具有更好的全局寻优能力.值得注意的是,本文的3 个算例中,v1和v2的优化均是典型的多峰值优化问题,梯度优化算法难以获得全局最优值,而C L P S O兼顾了效率和全局寻优能力.因此针对一般工程问题的FAFBS 算法中v1和v2优化,建议读者使用全局优化算法执行该过程,以保证获得最优的稀疏PC模型.

基于FAFBS 算法的PC 重构过程如图2 所示.

图2 全自适应前向-后向选择算法简化流程图Fig.2 Fully adaptive forward-backward selection algorithm flowchart

2 流场/声爆多源不确定量化应用

2.1 四维Park 函数近似

针对验证发展的基于FAFBS 的稀疏PC 重构算法的有效性,本节首先使用一个经典的四维Park函数算例进行验证,其表达式如下

式中,x1,x2,x3,x4为互相独立的均匀同分布随机变量.参考统计矩由MCS 方法基于 1 07个拉丁超立方抽样(Latin hypercube sampling,LHS)样本估计得到.全PC、基于OMP 和FAFBS 的稀疏PC重构均使用9 阶PC 候选多项式基,具体HS 截断格式可参考文献[35].全PC 指使用在阶数p截断后的全部多项式项进行最小二乘拟合,即 (p+d)!/(p!d!) 项.本文所有算例使用全PC 近似时,样本数均为N=2M=2(p+d)!/(p!d!).3 种方法所需样本数均使用LHS 获得.3 种方法近似Park 函数的均值和方差的误差收敛效率对比如图3 所示.结果显示,两种稀疏PCE 重构方法的收敛效率和近似精度显著高于全PC 方法,尤其基于FAFBS 的算法收敛效率最高.进一步地,当同时使用70 个样本时,基于FAFBS 的稀疏PC 重构方法近似的均值和方差误差分别为0.019 0 和0.069 6,而基于OMP 的FAFBS 方法的PC 重构方法的近似误差分别为0.587 1 和0.462 4.FAFBS 获得了明显更低的预测误差.详细计算结果分析对比如表2 所示.结果显示,相对于全PC 使用990 个样本和OMP 使用200 个样本,基于FAFBS 的方法仅使用170 个样本获得了0.001 1 和0.004 6 的显著更低的相对误差.此时在FAFBS 方法中两个阈值参数优化值分别为v1=0.1,v2=0.005.

图3 基于OMP 和FAFBS 重构的稀疏PC 以及全PC 的预测Park 函数统计矩的误差随样本数变化对比Fig.3 Relative error in mean and standard deviation of Park function using the OMP and FAFBS-based selection methods and full PC method

表2 使用全PC,OMP 和FAFBS 的PCE 方法预测的精度对比Table 2 Comparison of prediction error of park function using full PC,OMP,and FAFBS methods

为了验证样本分布的影响,基于110 个样本抽样100 次,分别使用这3 种方法预测Park 函数的均值和方差,所得相对误差的箱图对比如图4 所示.结果表明,基于FAFBS 方法预测的均值和方差的误差4 分位范围和中间值均远小于基于OMP 方法和全PC 方法得到的结果.并且基于全PC 和OMP 方法预测的均值和方差的误差异常值显著更大,也多于基于FAFBS 方法预测得到的误差异常值.这些结果均表明基于FAFBS 方法的稀疏PC 重构方法相对于OMP 和全PC 方法是更加可靠和有效的,可以满足复杂工程问题使用需求.

图4 使用全PC,OMP 和FAFBS 的PCE 方法预测Park 函数的均值和方差的相对误差箱图对比(基于110 个样本抽样100 次)Fig.4 Boxplots of relative errors in mean and standard deviation of Park function obtained using full PC,OMP,and FAFBS methods based on 100 runs using 110 sample points at each run

2.2 跨音速RAE2822 翼型流场不确定量化

跨音速流场对马赫数,攻角,湍流度和几何外形加工误差等变化时,气动力表现非常敏感.因此常常被用来测试不确定量化和代理建模技术精度等[36-37].本节使用RAE2822 跨音速流场验证发展的基于FAFBS 的稀疏PC 重构方法的准确性和有效性.本文考虑了对气动特性影响最敏感的两类不确定源,即来流状态不确定和加工误差不确定.本文假设马赫数和升力系数在名义状态点附近产生随机波动并服从正态分布,即Ma=µM+ξMσM以及 α=µα+ξασα,其中 µM=0.734,σM=0.01,µα=2.79°,σα=0.2°,并有ξM,ξα～U(-1,1).

本文模拟几何外形加工误差的不确定性通过引入高斯随机变量e(s,ω),其中s代表了沿翼型表面一周的空间位置(坐标),ω 为概率空间.e(s,ω) 表示翼型表面每个位置处沿表面外法向方向实际加工外形和名义设计外形之间的误差.加工翼型表面被近似为

其中n(s) 代表在s位置处的外法向.(s) 为名义外形.高斯误差函数e(s,ω)定义为 均值(s,ω) 和指数相关核函数R(s1,s2).核函数R(s1,s2) 描述了空间的任意两位置的光滑性和相关性,通过下式给出

式中 σ (s) 是随机变量在s处的标准差,暗示了该点处误差的变化,因而是一个非负实数.l为相关长度.对于RAE2822 翼型 0 ≤s≤2.032.

经典的K-L 展开对随机变量e(s,ω) 进行近似并降维,即

其中 ξi(ω) 指0 均值和单位方差的高斯随机变量,即ξi～N(0,12).为了方便,本文取所有点处的(s)≡0,λi和 φi分别表示核函数的特征值和特征函数.文献[38]给出了解析的特征函数表达式和特征值求解方法,这里不再赘述.特征函数的截断阶K通过保留原始随机过程最多的能量方式选取,即

得到K=12.因此本文使用K-L 展开的前12 项去近似随机变量e(s,ω),并通过测试选择σ=0.001 5 和l=0.2时,特征值随个数增加衰退速度中等,翼型扰动和压力分布变化均较为合适.因此,通过式(15)截断准则,本文选取前12 阶特征值和特征函数构成截断的K-L 展开,即使用12 个随机变量控制外形的随机分布影响,即 ξi～U(-1,1),i=1,2,···,12.因此,本算例总共考虑飞行状态与几何外形不确定性共14个不确定因素,即 Ξ=(ξM,ξα,ξ1,ξ2,···ξ12),他们均服从标准正态分布.

本文使用提出的FAFBS 算法、OMP 算法以及全PC 方法对上述问题建立PCE 近似.图5 和图6分别给出了扰动翼型的外形和表面压力系数的分布范围对比.图7 给出了使用3 种方法近似阻力系数均值(µCd)和方差(σCd)的预测误差的收敛曲线对比,其中参考值使用MCS方法基于 1 06个LHS 样本点获得.可以发现,当使用相同的样本数时,基于FAFBS 和OMP 的稀疏PCE方法相对于全PC 方法获得了显著更快的误差收敛特性.尤其FAFBS 持续获得了最快的误差收敛率和最准确的近似准确率.图8 给出了力矩系数均值(µCd)和方差(σCd)预测的近似误差收敛曲线对比,结果显示了相同的趋势.即比如当均使用70 个样本时,FAFBS 近似阻力系数均值和标准差相对误差分别为0.069 4 和0.156 8,明显好于OMP 的0.271 0和0.390 2.同样样本下,FAFBS 近似力矩系数均值和标准差相对误差分别为0.003 22 和0.108 97,仍然好于OMP 的0.090 06和0.381 19 的相对误差.表3给出了3 种方法近似气动系数的统计特性满足误差收敛标准时所选择的PC 项数和所需样本数.结果显示,当使用190 个样本时,FAFBS 选择了14 个PC项近似阻力系数统计特性误差在1 count (1 0-4)以内.而经典的OMP 使用210 个样本选择了29 项,全PC 基于680 个截断项使用了1360 个样本,此时他们预测误差均大于3 counts,而为了达到1 count 的预测误差则需要远远更多的样本.近似升力系数统计特性时也展示出了相同的趋势,即FAFBS 相对于其他两种方法,拥有更快的误差收敛特性和更可靠的误差预测准确率,可完全满足跨音速流场复杂气动不确定量和稳健设计需要.FAFBS 方法相对于传统MCS 方法在获得相同计算精度时,计算花费减少了3 个数量级.

图5 以RAE2822 翼型为中心的30 个扰动翼型(l=0.2,σ=0.001 5)Fig.5 30 disturbed airfoils around RAE2822 airfoil (l=0.2,σ=0.001 5)

图6 30 个扰动翼型的压力分布 (l=0.2,σ=0.001 5)Fig.6 Pressure distributions of 30 disturbed airfoils around RAE2822 airfoil (l=0.2,σ=0.001 5)

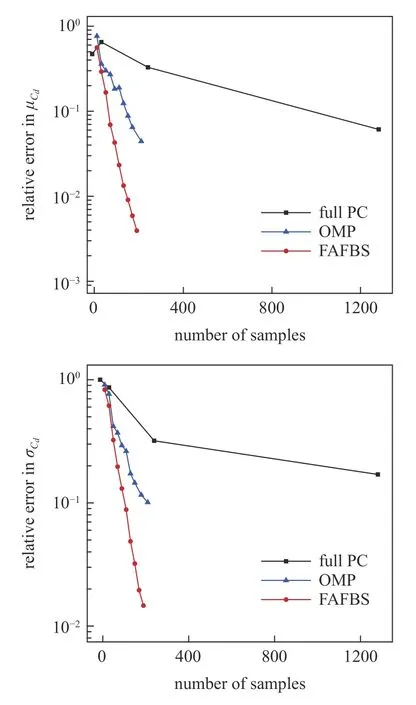
图7 使用FAFBS,OMP 以及全PC 等3 种方法预测阻力系数均值和方差的相对误差随样本数变化曲线Fig.7 Variation of relative errors in mean and standard deviation ofCd with increasing HF sample size using full PC,OMP,and FAFBS methods

图8 使用FAFBS,OMP 以及全PC 等3 种方法预测升力系数均值和方差的相对误差随样本数变化曲线Fig.8 Variation of relative errors in mean and standard deviation ofCl with increasing HF sample size using full PC,OMP,and FAFBS methods

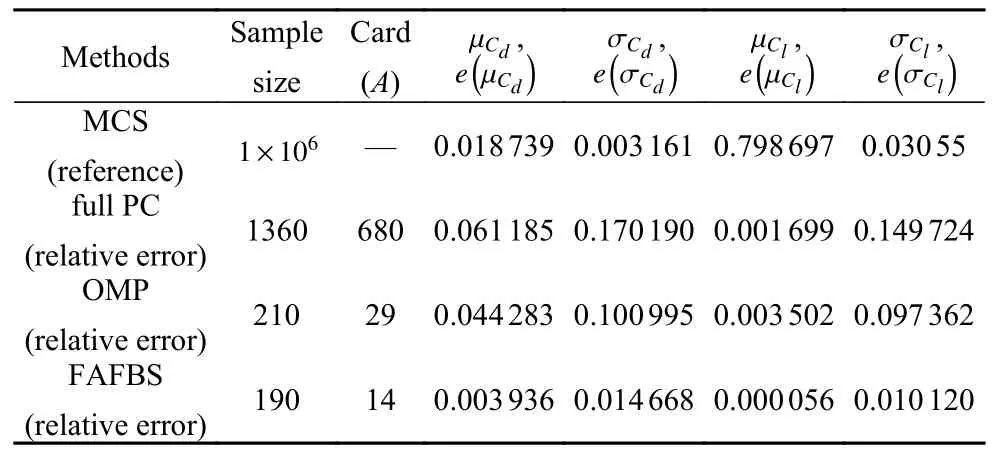
表3 使用全PC,OMP 和FAFBS 的PCE 方法近似气动系数统计特性的相对误差Table 3 Comparison of relative errors in approximating aerodynamics coefficients using full PC,OMP,and FAFBS methods

2.3 声爆不确定量化

音爆不确定量化已经得到了广泛的关注和许多研究机构的深入研究[8,39-41],如美国国家航空航天局(NASA)和日本航空航天研究机构(JAXA)[18]持续开展了此类研究.

本文主要考虑了温度T,湿度H,飞行高度L以及马赫数Ma这4 个相互独立的不确定变量.其中温度T和湿度H分布参考雅斯兰吉航天中心在瑞士的测量数据(2000 年—2009 年8 月)[18].温度T在高度98 ≤h≤31 376 m 被分为17 层,以及湿度H在高度90 ≤h≤9185m 分为8 个高度.两个因子的均值和标准差在每一层里的值是文献[18]中给出.本文假设温度T和湿度H是两个独立的正态分布变量,即µT(hi)+ξTσT(hi)(i=1,2,···,17)以 及µH(hi)+ξHσH(hi)(i=1,2,···,8),其中 ξT,ξH～N(0,12).每一层的 ξT和ξH均相同.此外,本文定义另外两个不确定变量飞行高度L和马赫数Ma也 为独立正态分布的,即µL+ξLσL和 µM+ξMσM,其中 ξL,ξM～N(0,12).在这个应用中,飞行高度均值 µL=16 764 m 以及标准差 σL=100 m,马赫数均值 µM=1.6 以及标准差 σM=0.1.因此,本算例总共考虑了4 个标准正态分布输入变量,即ξT,ξH,ξL和 ξM.

本文使用基于FAFBS 的PCE 方法建立近场波形的多项式混沌代理模型.如图9 和图10 所示,FAFBS 方法使用20 个样本修建的稀疏多项式混沌获得了和参考值几乎重合的标准差和均值分布.其中参考的地面波形标准差和均值均是通过MCS 方法基于10 000 个样本计算得到的.图11 和图12 分别给出了标准差和均值近似相对误差分布(0.083 ≤t≤0.415 s).结果显示,当仅仅使用20 个样本时,均值和标准差近似的最大相对误差在左右.而随着样本数增加到100 时,不同时间点处相对误差均明显减小.图13 给出了对地面波形近似的 ± 2σ 带分布.

图9 FAFBS 方法近似地面波形标准差分布Fig.9 Comparison of estimated standard deviation of ground signatures between by FAFBS and MCS methods

图10 FAFBS 方法近似地面波形标准差相对误差分布Fig.10 Relative error of estimated standard deviation of ground signatures by FAFBS with different samples

图11 FAFBS 方法似地面波形均值分布Fig.11 Comparison of estimated mean of ground signatures between by FAFBS and MCS methods

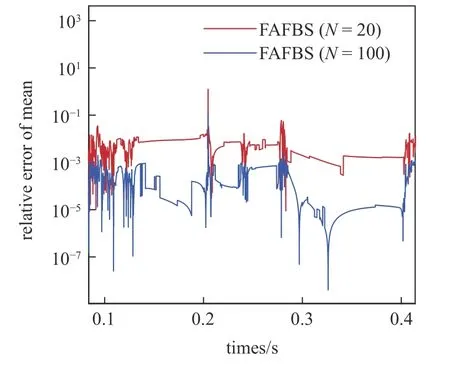
图12 FAFBS 方法近似地面波形均值相对误差分布Fig.12 Relative error of estimated mean of ground signatures by FAFBS with different samples

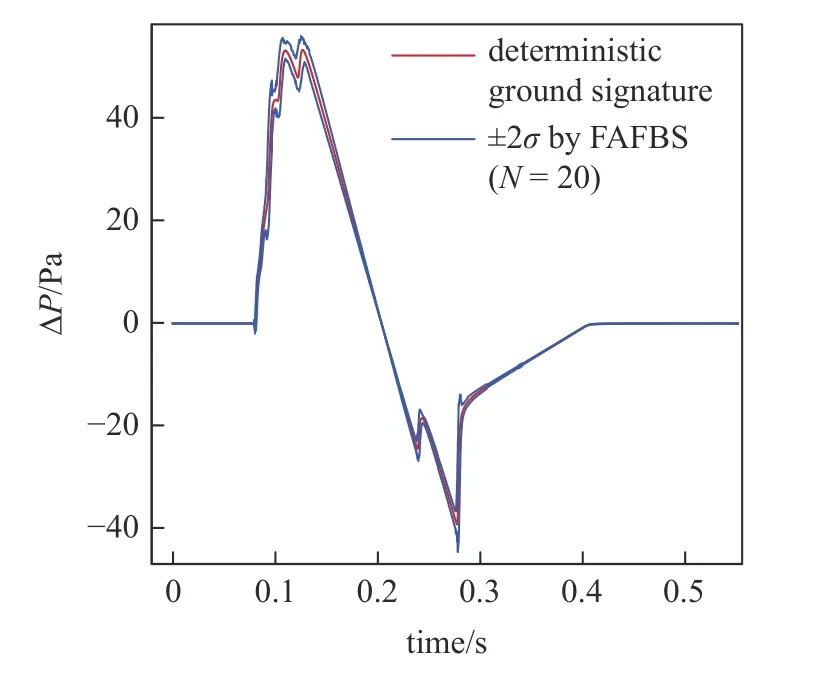
图13 使用FAFBS 方法近似的地面波形 ± 2σ 分布Fig.13 Estimated ± 2σ bounds of ground sonic boom signatures by FAFBS based on 20 samples

进一步,使用FAFBS 算法、OMP 算法以及全PC 方法分别对感受音强水平(PLdB)进行不确定量化.表4 所示给出了全PC,LAR 以及FAFBS 方法修建的多项式混沌近似PLdB 统计矩误差对比.结果再次表明稀疏PCE 在相同的样本数下获得了明显更好的近似准确率.FAFBS 方法使用60 个样本仅仅选择了5 项最重要的PC 基,分别获得了e(µs)=0.002 98% 和e(σs)=0.094 0% 的最低近似误差.而全PC 使用多达660 个样本,获得了e(µs)=0.025 75%以及e(σs)=1.725 0% 的最大近似误差.图14 的结果也进一步显示,FAFBS 方法准确恢复了5 个最大的PC 基系数,而LAR 方法选择了一些非常小的PC 基系数,引入了噪声,以至于LAR 方法没有准确恢复一些最重要的PC 基系数.3 种方法建立的PCE 近似的收敛性分析如图15 所示.FAFBS 方法获得了最快的误差收敛率以及最小的近似误差,而全PC 方法收敛最慢.当使用80个样本时,FAFBS方(法近)似均值和标准差的近似误差分别达到了,而全PC和LAR方法要达到相同的近似准确率,却需要远远更多的样本.

图14 FAFBS 和LAR 方法近似PLdB 恢复的多项式系数与参考值对比Fig.14 Recovered PCE coefficients by FAFBS and LARs-based techniques compared with the reference coefficients obtained by GPNIPC with sufficient samples

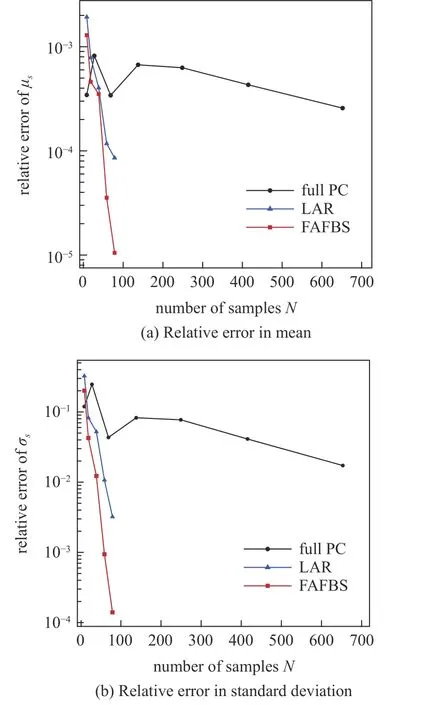
图15 使用FAFBS,LAR 以及全PC 方法近似PLdB 均值和标准差的相对误差随样本数变化Fig.15 Comparison of variation of relative error in mean of PLdB using FAFBS,LAR,and Full PC methods.

表4 使用3 种方法修建的多项式混沌近似感受音强水平(PLdB)均值和标准差相对误差对比Table 4 Comparison of estimated moment of perceived noise level (PLdB) using three methods

通过分析也可以发现,OMP 或者LAR 这类前向选择算法在自适应基选择过程中,不断挑选新的基函数进入活跃集合,然后拟合活跃集合中的所有多项式项获得PC 系数,即同时最小化 β1和截断误差.然而,在实际问题中,由于样本量通常较少,自适应基选择过程中会不可避免地引入误差导致一些不重要的基被选入,使得OMP 或者LAR 难以获得最稀疏的多项式基集合和最优的PC 近似.FAFBS 相对于OMP 或LAR 通过全自适应的前向-后向选择过程,使得活跃集获得最优的多项式集合,进而提高了近似准确率.同时FAFBS 剔除掉不重要的基函数,避免拟合这些基函数带来的噪声影响,提高了稀疏多项式混沌重构的可靠性.此外,对于一般的工程问题,输入变量的分布通常是未知的,并且可能是相关或者离散的.此时可以基于输入样本数据,构建基于数据驱动的aPC 基[42-43],然后结合FAFBS 高效算法,建立适用于一般问题的最优稀疏PC 模型.

3 结论

随着飞行器各种性能要求的不断提高和先进计算力的发展,在设计过程中考虑各种可能的不确定源的影响并设计出具有稳健性能表现的飞行器具有重要意义.然而考虑多源不确定性的气动不确定量化方法如MCS 以及全PCE 等方法均无法避免高昂的计算花费,并且适应性差,难以满足飞行器复杂流场/声爆不确定量化需求.针对这一难题,本文提出了一种基于FAFBS 的高效稀疏PC 重构方法.它通过全自适应前向选择-后向检查-迭代筛选等步骤自动选择对所近似系统最优的稀疏PC 基,解决了经典前向选择算法如OMP 和LAR 等无法剔除已入选冗余PC 基而导致拟合噪声,以及典型后向剔除算法总是剔除过多造成过拟合等难题,显著加强了PC 基近似的稀疏性和可靠性.

基于发展的高效稀疏多项式混沌重构方法,本文开展了考虑多源不确定性的流场/声爆不确定量化研究,包括经典的Park 函数、考虑加工误差和飞行状态参数不确定的跨音速RAE2822 翼型复杂流场不确定量化以及考虑温度、湿度、飞行高度和马赫数不确定的经典音爆不确定量化等3 个应用.结果均显示,基于FAFBS 的稀疏PC 方法获得了最快的误差收敛率以及相同样本下最小的近似误差,基于LAR 或OMP 的稀疏PC 方法的收敛率显著慢于FAFBS 方法,而原始的全PC 方法收敛最慢,相同样本数下误差也最大.进一步对比发现,对于采用70个样本进行跨音速流场不确定量化时,基于FAFBS的稀疏PC 方法近似跨音速RAE2822 翼型流场的阻力系数均值和标准差相对误差分别为0.069 4 和0.156 8,明显好于基于OMP 的稀疏PC 方法的0.271 0 和0.390 2.继续增加样本时,FAFBS 相对于OMP 方法的优势更加显著.同样,当基于80 个样本进行音爆不确定量化时,基于FAFBS 的稀疏PC 方法获得的感受音强水平均值和标准差近似误差分别为,而全PC 和基于LAR 的稀疏PC 方法要达到相同的近似准确率则需要远远更多的样本.相对于直接使用蒙特卡罗模拟方法进行不确定量化,使用基于FAFBS 的稀疏PC 方法在达到相同矩估计准确率时,计算花费减少3 个数量级,可完全满足高效飞行器复杂流场/声爆多源不确定量化以及多学科稳健优化设计需求.

附录A 声爆数值分析验证

准确的音爆预测与分析是超声速飞机设计的关键技术[44].本节首先采用SBPW-2 会议给出的两个标准算例验证课题组程序的准确性.其中Lockheed Martin 1021 (LM1021) 是洛马公司设计的一型新一代超音速客机布局,Axibody 为一个简单的几何回转体,他们的三视图和外形分别如图 A1 和图A2 所示.图 A3 给出了课题组开发的计算程序[45]与sBOOM计算地面波形对比.LM1021 预测结果显示,二者的预测波形基本相似,二者 0°周向角的结果基本重合,3 0°周向角的结果在0.275 s 处有所偏差.而针对Axibody 算例,在两个周向角下,两者的计算结果都比较接近,预测精度基本相当.然而,音爆传播到近场波形受大气不确定性的影响非常敏感,以至于开展音爆不确定分析已经成为稳健低音爆超声速飞机设计的重要部分[39].

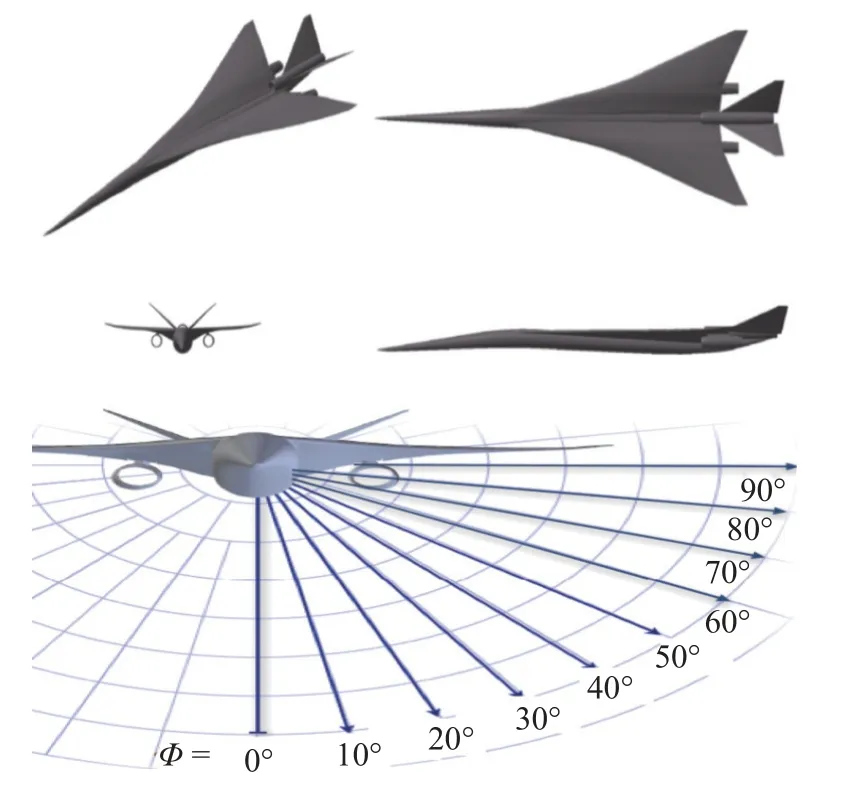
图A1 LM1021 外形[39]Fig.A1 The configuration of LM1021[39]

图A2 Axibody 几何外形Fig.A2 The configuration of Axibody

图A3 课题组程序与sBOOM 对(a) LM1021 和(b) Axibody 外形的预测地面波形比较(采用SBPW 给出的标准大气,相对湿度为70%)Fig.A3 Comparisons of ground signatures in 2nd SBPW against sBOOM for (a) LM1021 and (b) Axibody (atmospheric conditions:standard atmosphere profile,constant relative humidity of 70%,rolling angle: 0°)

附录B 跨音速流场数值分析验证

RAE2822 翼型是经典的超临界翼型,经常被用来验证数值分析和优化设计方法[36].这里选取的典型计算状态为:Ma=0.730,Re=6.5×106,以及Cl=0.800.表B1 给出了RAE2822计算所使用3 套计算网格.网格为C 型拓扑,远场距离为50 倍翼型弦长,湍流模型均使用两方程SST.图B1 给出了数值模拟结果与试验值压力分布对比.可以看出,随着网格密度增加,数值模拟结果与试验结果吻合越来越好,对激波位置和强度的捕捉也更为准确.图B2 给出了数值计算结果与试验气动力系数的对比.结果显示,使用密网格计算所得阻力系数与试验值误差为0.000 200 7,升力系数误差为0.005 3,可以满足气动分析与优化设计需求.

图B1 RAE2822 不同计算网格近场及远场展示Fig.B1 Spatial mesh around RAE2822 with different sizes

图B1 RAE2822 不同计算网格近场及远场展示 (续)Fig.B1 Spatial mesh around RAE2822 with different sizes (continued)

图B2 不同网格计算压力分布与试验压力分布对比Fig.B2 Spatial mesh around RAE2822 with different sizes