基于洛仑兹曲线模型的中等收入定位研究

周文浩

摘   要：以洛仑兹曲线和中等收入问题为研究对象，对收入分配的分组数据进行拟合，得到参数估计值和均方误差，发现其与现有的10种洛仑兹曲线相比具有更好的模拟效果。然后利用收入空间法、人口空间法定义中等收入人口。最后利用基尼系数和极化曲线的思想，给定两种定义的中等收入人口的测算方法和数学模型。

关键词：洛仑兹曲线；收入空间法；基尼系数；中等收入

中图分类号：F01       文獻标志码：A      文章编号：1673-291X（2023）17-0004-03

一、洛仑兹曲线模型

通过数学和统计学的相关概念，这里假设收入分配的密度函数为f（x），其对应的分布函数为F（x），且假设F（x）的反函数存在，记为F-1（p）。记收入低于或等于x的人口群体占有的收入占总收入的比例为L（p），则应有

L（P）称之为收入分配的洛伦兹曲线。目前学界相关的拟合模型有以下几种，包括几何计算法、分布函数法与曲线拟合法，几何计算法由于其根据几何图形分块来计算基尼系数，因此相对比较粗糙，分布函数法分析较为复杂，在实际研究中的应用较少，故本文拟采用曲线拟合法，应用非线性最小二乘法对模型的参数进行估计。

非线性最小二乘法是一种比较实用的参数估计方法。其原理如（2）式所示。

确定其中参数向量τ的估计值τ，然后用L（p，τ）=L（p）作为近似的洛伦兹曲线来进行收入分配分析，其中L（p，τ）是定义在[0，1]区间上、取值于[0，1]区间的函数，满足

即L（p，τ）在[0，1]上是凸增函数。本文将在后面的研究中略去参数τ以求表述简练。

接下来本文将设置合适的模型使L（p，τ）满足条件（3），近年来，不少学者提出了各式各样的参数洛仑兹曲线模型。Sarabia构造了形如S（p）=PaL（p）η的模型，其中L（p，τ）是参数洛仑兹曲线模型，Sarabia的模型成立的条件比较苛刻，见定理1：

定理1 当α≥0且η≥1，L（p，τ）的三阶导数L'''（p，τ）≥0，此时S（p）=PaL（p）η满足洛仑兹定理的条件。

因为Sarabia的定理要求非常严格，而且η≥1的条件大大限制了模型的拟合效果。王祖祥在Sarabia研究的基础上改进了定理1，提出了定理2：

定理2 设L（p，τ）满足洛伦兹曲线的条件且对于任何p∈[0，1]，有L'''（p，τ）≥0，则当α≥0，η≥1/2，α+η≥1时，PaL（p）η满足洛仑兹曲线的条件。

接下来进行参数变换转化成可以应用无约束最小二乘法进行参数的估计。

令α=（1+α2）sin2b，η=（1+α2）cos2b，β1=sin2c，β2=sin2d（5）

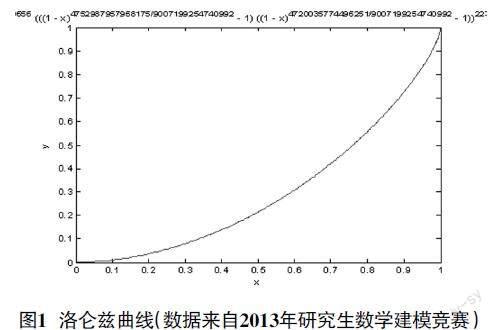
使用Levenberg-Marquardt算法求解非线性最小二乘问题，以估计其中参数。运用matlab软件可以得到a，b，c，d的估计值分别为0.7849，1.1682，0.8131，0.8058。将参数带入（5）（4）式进行拟合可以得到下图：

上述拟合精度的好坏可以采用以下三种标准进行比较。

均方误差（MSE，mean squared error）：

平均绝对误差（MAE，mean absolute error）：

最大绝对误差（MAS，maximum absolute error）

在这里我们采用第一种标准均方误差，求得MSE=

5.7891e-005，表明模型拟合精度高。

二、收入空间法和人口空间法

对于中等收入者的界定是目前学界研究的一个焦点问题，一般有两种界定方法，一种是根据给定的收入来界定，比如国家统计局城调总队课题组提出家庭年收入6万—50万元为我国的中等收入上下限以及国外的一些定性观点；另一种是根据人口比例来界定，主要有固定比例界定方法和食品收入占比的恩格尔系数界定方法。

中等收入是指在收入方面相对高收入和低收入处于中等水平的一种状态。中等收入受空间条件制约，指它在不同地域受当地条件限制而有所差别。我国各地区的发达程度有明显的地域差别，目前东部地区中等收入水平高于中西部中等收入水平，城市中等收入水平高于农村的中等收入水平。收入是可量化指标，中等收入当然也可量化，由此需要数值化的指标来度量中等收入。中等收入者是指全部有收入的人群中，相对于高收入者和低收入者而言，处于中等水平的一个群体。因此，中等收入水平必定是个区间，有上接近高收入人群的上限和下接近低收入人群的下限，而不是一个指标值。

收入空间法方面本文提出按照中位收入的一个比例来确定我国中等收入者的收入区间，其依据如下：在存在经济进步或通货膨胀的情形下，收入区间的右移也会导致收入中位数的右移，这也克服了收入取值的任意性。

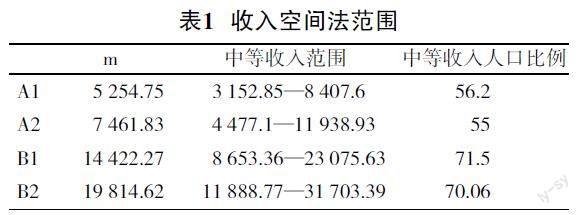
相关数据来自2013年全国研究生数学建模竞赛E题：假设收入属于（xl，xh）中的人口为中等收入人口，其中xl=0.6m，xh=1.6m，此时可以求出中等收入范围和中等收入人口的数量或范围。

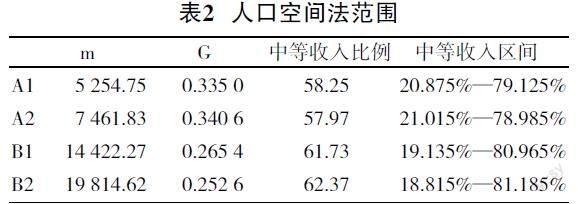
在人口空间法方面本文将采用基尼系数的方法来确定中等收入人口比例，假设基准中等收入人口比例为60%，基准基尼系数为0.3。当基尼系数提高时，收入区间变得更加稀疏，两级分化程度加剧，从而中等收入比例降低，假设实际基尼系数为G，中等收入比例MF为：

很显然，当基尼系数低，即两级分化程度也较低时，中等收入水平提高，比如基尼系数为0.1时，中等收入比例为70%；当基尼系数较高时，中等收入水平较低，比如基尼系数为0.9时，中等收入比例仅为30%。另外在确定人口区间时，假设比例在50%的两端（即中位数两端）均匀分布，比如当中等收入比例为60%时，中等收入人口区间为20%—80%。根据相关数据可得表2。

地区A相对年份1来说，年份2的中等收入人口的比例有所降低，地区B则是第二年的中等收入人口比例有所增加，从表中可以发现中等收入人口比例与基尼系数的对应关系。

三、基尼系数与极化曲线

根据已经得到的收入分配的洛仑兹曲线，我们可以得到描述收入不平等的基尼系数。

收入分配的两极分化反映出贫富差距越拉越大，不利于社会资源的正常流动，财富的过于集中和分化会导致“中产阶级”的空洞化。Wolfson提出了一种两极分化指数，先定义所谓的第一类极化曲线：

其中F-1是收入分配分布函数的反函数，再定义第二类极化曲线：

其中μ是平均收入，L（p）是洛仑兹曲线，最后可以定义两级分化指数为：

W越大，两级分化越严重，中等收入人口比例也随之下降，又因为W∈（0，1），因此可以设计中等收入比例指数如下所示：M=1-W，很显然M∈（0，1），且M越大，中等收入比例越大，反之亦然。

四、模型分析

地区差异和时间差异是我们研究的两个维度，具体的数据来自2013年研究生数学建模竞赛，数据说明了两个地区不同年份居民收入的动态变化。下面分别从基尼系数和中等收入指数的角度进行分析并画出洛仑兹曲线。根据模型（4）进行非线性最小二乘法估计参数并拟合。

由表3可以发现A地区从第一年到第二年基尼系数升高，而中等收入比例增大；B地区从第一年到第二年基尼系数降低，而中等收入比例降低。富裕的地区基尼系数较小而且第二年得到了改进，而较不富裕的地区随着年份的增长，基尼系数反而上升。因此提高全民的收入，让收入区间右移间接降低了基尼系数，改善了收入分配。

中等收入指数的变化趋势与基尼系数是一致的，即收入不平等的加剧会降低中等收入人口，同时两极的人口数得到了增长。

通过模型（4）求出洛仑兹曲线并采用Matlab分别对两个地区不同年份的曲线进行绘制，如图2所示：

图中从上至下分别为B2、B1、A1、A2，研究发现B地区第二年收入分配的不平等程度最低，同时A地区的不平等程度显著高于B地区；A地区第二年收入分配的不平等程度上升而B地区第二年收入分配的不平等程度下降。收入分配的不平等程度与基尼系数的变化是一致的。

五、模型评价

一是对洛仑兹曲线模型的构建参考了Sarabia的定理进行了建模，模型参数较多可以很好地满足题设条件，文中应用非线性最小二乘法拟合洛伦兹曲线模型是比较理想的方法。但是模型的拟合精度仍然不够高，后续的研究可以考虑在模型中加入5個或5个以上的参数。二是对收入空间法和人口空间法分别运用了中位收入基准法和基尼系数基准法，模型简明扼要，结果比较直观，缺点是模型的复杂度有待提高。三是参考Wolfson的两极分化指数来构建中等收入指数，模型比较合理，较好地解决了中等收入指数的测算问题。

参考文献：

[1]   王祖祥，范传强，何耀，等.农村贫困与极化问题研究：以湖北省为例[J].中国社会科学，2009（11）：73-88.

[2]   Sarabia J M，Castillo E，Pascual M，Sarabia M.Mixture Lorenz curves[J].Economics Letters，2005（89）：89-94.

[3]   李培林．扩大中等收入者比重的对策思路[J]．中国人口科学，2007（5）：46-52．

[4]   Duangkamon Chotikapanich and William E. Griffiths.Estimating Lorenz curves using a Dirichlet distribution[J]．Business and Economic

Statistics，2002（20）：290-295.

[5]   王红霞.基于一族新洛伦兹曲线的收入不平等测度：以湖北省城镇及农村的收入数据为例[J].经济评论，2009（3）：22-28.

[6]   Duangkamon Chotikapanich，D.S.Prasada Rao，Kam Ki Tang.Estimating income inequality in China using grouped data and the generalized Beta distribution[J].The Review of Income and Wealth，2007（53）.

[责任编辑   文   欣]