收入增长下基尼系数的变动研究
艾小青
(1.北京工业大学 经管学院,北京 100124;2.首都社会建设与社会管理协同创新中心,北京 100124)
一、问题的提出
党的十八大提出居民收入倍增计划,2020年实现城乡居民人均收入比2010年翻一番,这也意味着收入年均增长率要达到7.2%。收入增长对低收入群体而言尤为重要,2013年国家统计局发布了中国过去10年的基尼系数值,并特别指出:我国的基尼系数值较高,为缩小收入差距,我们的分配要做得更好,中低收入居民的收入力争要增加得更多一些。人力资源和社会保障事业发展统计公报显示,2014年全国共有19个地区调整了最低工资标准,平均增长幅度为14.1%。对社会总体而言,收入增长特别是中低收入群体的收入更快增长,对于减小贫富差距有着重要的作用。
在收入增长的现实背景下,反映收入差距的基尼系数将如何变动?本文将深入分析收入增长和基尼系数变动的理论关系,定量研究和测度确定性收入增长、不确定收入等因素对基尼系数变动的影响,并给出在各种情况下基尼系数的走向趋势,为政府部门调整收入分配政策提供理论和数据支撑。
有关基尼系数的研究成果很多,但专门针对收入增长下基尼系数变动的研究很少。徐宽系统总结了基尼系数的研究文献在过去80年是如何拓展的,梳理了国外基尼系数研究的主要发展脉络和理论成果[1]。我国近年对该领域的研究主要包括对基尼系数内涵、计算方法和统计推断的理论研究[2][3][4][5],以及用基尼系数测度收入等社会经济变量不平等程度的应用研究[6][7][8][9]。周兴从实证分析出发,提出我国基尼系数不断增加是由于收入增长的累进性对收入差距的负向效果被收入的流动性所抵消而造成的[10]。本文将立足现实背景,从理论模型出发研究收入增长下基尼系数变动的理论性质。本文研究的新意在于:(1)基于各期收入分布函数计算基尼系数,挖掘基尼系数变动的内在影响机制;(2)当期收入是在前一期收入的基础上,结合收入增长的内涵而生成的随机变量,从而得到了时间序列上的各期收入分布函数;(3)通过计算机模拟,分析和揭示基尼系数的纵向变动,并给出定量的模拟分析结果。
二、模型的设定
国家统计局从2012年开始为计算基尼系数而使用最新的可支配收入指标,其构成包括工资性收入、经营净收入、财产净收入、转移净收入和自有住房折算净租金等[11]。从数理性质出发,我们认为工资性收入属于确定性收入,其他收入来源属于不确定收入。
设社会总体中个体数量为n,在报告期第t期(年),个体i的收入构成包括确定性收入、不确定收入以及随机波动,即:

其中:

随机变量Rti表示确定性收入之外的奖金、分红等不确定收入,取值大于等于0,设置Rti的分布及参数时,需考虑时间的纵向关系以及不同个体的差异性,使得富人比穷人在不确定收入的期望值和方差上都更大。随机变量εti表示收入的随机波动,取值有正有负,我们假定εti服从期望为0、方差为σ2ti(异方差)的正态分布。
由式(1)和(2)还可以看出,报告期的收入与上一期的收入有关,对于社会总体而言,各期的收入分布也是前后关联的,并且都受到基期收入分布的影响。
本文目的在于考察基尼系数变动与收入增长的关系,通过构建模型利用计算机模拟,从定量上解答以下几个问题:(1)确定性收入增长率不同和基尼系数变动的定量关系如何?(2)不确定收入以及收入随机波动,整体上将降低还是提高收入的不平等程度,基尼系数的结果是减小还是增加?(3)各种因素共同作用时,基尼系数将如何变动,以及各个因素作用力的大小?

该模型的意义在于:在基期收入分布的基础上,确定性收入的增长、不确定收入和随机波动将对基尼系数在时间轴的变动产生什么样的短期和中长期影响。
基于模型对各期基尼系数的求解,理论上可以利用各期的收入分布函数进行积分计算,但由于各期收入分布函数是一个复杂组合,直接计算非常困难,而通过计算机模拟能够帮助我们得到结果。在本文研究中,我们将基于分布函数进行大样本随机数据模拟,得到实际的数据,从而根据离散数据计算未来各期的基尼系数(在大样本下与理论值近似相等)。我们将首先针对基期收入,介绍几种分布函数,以及相应的基尼系数表达式。
三、收入分布及基尼系数
现实中的收入分布通常都是单峰右偏的,学者通常以甘玛分布、帕累托分布、对数正态分布等进行拟合[12][13][14]。表1总结了这些分布的特征,三种分布下的基尼系数值都只与尺度参数α有关,并且σ越大,基尼系数值越大。

表2 分布函数及其基尼系数表达式
本文还设计得到了一种特定的收入分布洛伦茨曲线。设社会总收入为1,X0i表示在基期第i个个体的收入,不失一般性,设X01≤X02…≤X0i…,i=1,2,…,n,则收入不超过X0i的个体占人口总量的比重为i/n,他们占有收入总量的比重为。
为拟合基期收入的不平等状况,我们采取如下函数形式确定每个个体的基期收入:

离散数据的洛伦茨折线为(横坐标为i/n,纵坐标为P0i):

其中,k>1,系数k值越大,基期收入分布越不平等。总收入设为1,利用离散数据计算基尼系数,公式为:

当n趋于无穷大时,得到平滑的收入分布洛伦茨曲线,为:

利用分布函数计算基尼系数,结果为:

Lk(p)是本文设计得到的特定收入分布(命名为K 分布)下的洛伦茨曲线,k为控制收入不平等状况的参数,k>1,k越大,收入差距越大,相应的基尼系数值越大。基尼系数可以基于离散数据采用式(6)计算,也可以基于分布函数把k值直接代入式(8)计算,显然后者更加简单。在大样本下,两个结果差别不大,笔者分别用两种方法计算基尼系数,测算后发现只需样本量为100时,两个结果几乎就没有差别。
我们借助以上四种分布函数形式作为基期的收入分布。为进行数据模拟,还需确定分布函数中的未知参数。国家统计局发布2012年我国基尼系数值为0.474,不妨以2012年为基期,通过调整相关分布的参数,使得相应的基尼系数值等于0.474,计算结果是:甘玛分布的α=1.121;帕累托分布的α=1.555;对数正态分布的σ=0.897,K 分布的k=28。相关分布的其他参数可以根据期望值的大小进行设置,由于它们对基尼系数的值没有影响,本文不做专门讨论。同时,由于基期的收入构成不便分解,本文在模拟研究部分把基期收入作为确定性收入,该处理不影响对基尼系数变动的考察。
本文研究视角不是对收入分布的估计或拟合,而是以基期的收入分布为起点,进行模拟研究,探索因为收入的后续变化而造成的基尼系数的变动规律。本文设定基期的四种收入分布,主要是为了考察和验证分析方法及结论的稳健性。同时为保证模拟结果的可信度,样本量n=10000(实际上n>1000时结果一般就比较稳定了)。接下来我们将具体分析各因素对基尼系数变动的影响。
四、各因素对基尼系数变动的影响
(一)确定性收入增长
1.收入增长率的不同对基尼系数变动的影响
人们都有感性的认识,若穷人的收入增加更快,贫富差距和基尼系数将会减小。我们通过模拟研究来揭示收入增长率的不同与基尼系数变动的量化关系,只考虑确定性收入,第t期和上一期的收入关系为:

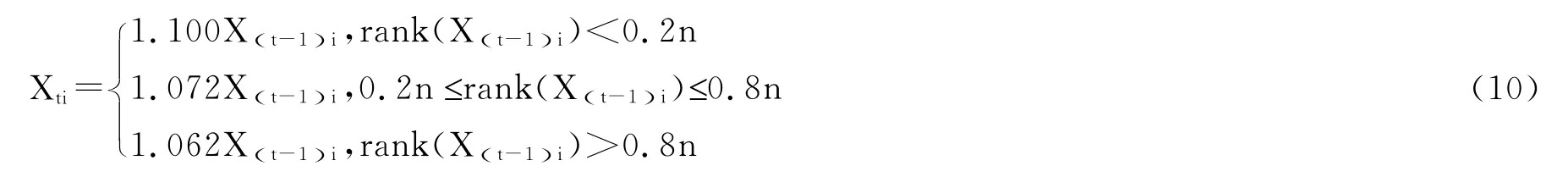
我们以2012年为基期,分别以四种收入分布函数作为基期的收入分布,首先确定相应的参数值,再通过计算机模拟生成基期的收入数据(样本量n=10000),然后根据收入增长率计算未来的收入数据并计算各期的基尼系数。表2揭示了不同收入分布函数下未来10年的基尼系数变动。

表2 基尼系数变动的模拟结果
从表2可以看出基尼系数都在稳定地逐年递减。帕累托分布下每年约减小0.005,其他三种分布下每年约减小0.003,10年之后减小0.03至0.05不等。可见,在保证低收入群体收入稳步增长的基础上,只需让中等收入群体的收入增长率比高收入群体高1个百分点,基尼系数就有相对明显地减小,而且这种减小的趋势是稳定的。我们还进行了不同的收入增长率设置和模拟,揭示了一般性的规律:当中等收入群体有较快的收入增长时,基尼系数会稳定下降,收入增长相对越快,基尼系数下降得越快,并且不同分布下的规律是一致的。
2.从个人所得税看收入增长对基尼系数的影响
个人所得税可以理解为收入的确定性负增长,各个国家和地区,基于一定的收入标准,征收不同档次税率的个人所得税。简单地说就是,穷人不纳税(达不到起征点)或少纳税(税率低基数小),富人多纳税(税率高基数大)。以美国为例,据美国国会预算办公室(CBO)发布的数据显示,2009年50%的低收入纳税人只缴纳了3%的个人所得税,而5%的高收入纳税人的缴纳比重高达60%;从平均实际税率来看,最低20%收入家庭平均实际税率为-9.3%(政府补贴),中产阶层家庭为1.3%,最高20%收入家庭为14%左右。通过个人所得税机制下的收入再分配,可以很大程度上降低社会总体的收入不平等程度。
OECD 国家官方会公布两个基尼系数,分别基于税前和税后的收入进行计算[15],从表3可以看出,各个国家税后基尼系数都明显小于税前。中国目前的基尼系数与发达国家税前基尼系数差别不大,但远高于它们的税后值,这一方面说明发达国家有效利用了个人所得税机制调节收入分配,极大地缩小了收入差距;另一方面也给中国的相关政策制定和执行提供了参考依据,个人所得税是调节收入分配的强有力手段,在实现收入公平分配职能方面发挥着极其重要的作用,中国还有较大的使基尼系数缩小的空间。

表3 2005~2010年OECD 主要国家税前、税后基尼系数
(二)不确定收入和随机波动
1.不确定收入对基尼系数变动的影响
不确定收入整体上将降低还是提高收入差距,相应地,基尼系数的结果是减小还是增加?由于这部分收入是不确定的,个体增加的结果不同,对比两人的收入差距可能减小也可能增加,整体的收入差距可能被消减也可能被增加,这其中是否存在概率上的一般性规律?
我们认为,在现有收入差距较大的情况下,若人们还有其他不确定收入来源,并且这个渠道对不同人群是相对公平的,这样将有较大的可能性缩小收入差距。举一个较为极端的例子:如果人们都有较大的概率得到一笔不菲的额外收入,并且它的额度对不同人是一样的,这样人们都有较大概率成为高收入者,收入差距将没有原来的大,基尼系数则会减小。当然,在现实中不同人得到不确定收入的概率和额度是不一样的,本文通过构建模型进行更一般意义上的模拟研究,只考虑不确定收入因素,第t期和上一期的收入关系为:

Rti是一个随机变量,取值大于等于0,不失一般性,我们以半正态分布作为Rti的分布:

同时考虑到时间和不同个体的差异性,对于收入较高群体而言,其下一年收入不确定增量的期望和方差都应较大,不妨令,使得个体的收入值越大,其下一年不确定收入的期望和方差也越大。
第t 期的基尼系数为:Gt=,图1揭示了不确定收入下基尼系数的变动。从中可以看出,不同群体的不确定收入缩小了收入差距,四种收入分布下基尼系数都在稳定地逐年递减,平均而言每年减小0.002至0.003不等,10年之后减小0.02至0.03不等,考虑到基尼系数变动的数量级一般较小,这样的减小幅度仍是比较明显的。可见,若能为民众提供相对公平的其他创收渠道,即使富人不确定收入的期望值在绝对数上要高于穷人,但相对而言同样能够起到缩小贫富差距的作用,从而减小基尼系数,并且这种减小的趋势是稳定的。
2.随机波动对基尼系数变动的影响
我们认为收入的随机波动,对基尼系数的变动没有系统性的影响。本文依然通过模型进行模拟验证,只考虑随机波动因素,第t期和上一期的收入关系为:

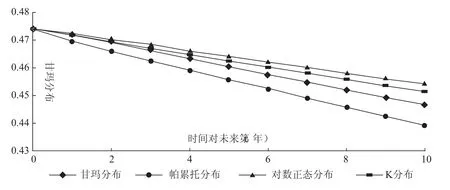
图1 不确定收入下基尼系数的变动

图2 收入随机波动下基尼系数的变动
3.共同作用
在各种因素的共同作用下,基尼系数将如何变动?哪种因素的作用力更强?我们认为,中低收入群体较高的确定性收入增长率,以及对所有群体相对公平的不确定收入,两者共同作用将使得基尼系数较快地稳定减小,并且前者的作用力更强。本文通过如下模型进行验证:

在上面的模型中:基期的收入分布以甘玛、帕累托、对数正态和K 分布为例;确定性收入的增长率分别对收入最低20%、中间60%和最高20%的群体赋予不同的值;不确定收入是一个随机变量,取值大于等于0,服从与时间和个体效应有关的半正态分布;收入随机波动是一个随机变量,服从异方差的正态分布。
为考察基尼系数的变动以及各因素作用力的相对大小,我们基于表2中同样的参数设置,即以2012年为基期,保证基期的基尼系数为0.474,不同收入段群体的确定性收入增长率不同,中低收入群体的值较大,分别为7.2%和10%,高收入群体的值较小,为6.2%,进行数据模拟,并计算未来10年基尼系数的变动值,以及各因素导致基尼系数变动的大小。
共同作用下基尼系数的减小值为:

确定性收入增长单独作用下基尼系数的减小占总减小值的比重为:

结果如表4和表5所示,由它们可以看出:
(1)由于中低收入群体有相对较高的确定性收入增长率,以及不同收入群体相对公平的不确定收入,对收入差距有所缓冲和消减,使得基尼系数在逐年减小,10年之后将减小0.04至0.06不等,并且不同分布下的变动规律是一致的。
(2)确定性收入增长率对减小基尼系数的作用力最强,其单独作用导致的减小值占总减小值的比重,不管基于何种分布或是哪个时期,都高达70%以上。可见,要解决收入分配不均,最好的办法是让富人实现收入增长的同时,穷人的收入增长更快一些。

表4 确定性收入增长、不确定收入等因素共同作用下基尼系数的变动

表5 确定性收入增长导致基尼系数减小的比重 (%)
五、结论
本文首先阐述了收入的构成包括确定性收入、不确定收入以及随机波动,并且建立了一个考察基尼系数变动与收入增长关系的理论模型;然后利用甘玛、帕累托、对数正态、K 分布(本文所设计)等四种分布函数作为基期的收入分布,分析了基期基尼系数与收入分布函数的关系。本文通过计算机模拟定量测度了模型中确定性收入增长、不确定收入等因素对基尼系数变动的影响,研究发现:在中国现有收入差距较大的情况下,若能保证中低收入群体有较高的确定性收入增长率(或者较低的个人所得税税率),以及不同群体有相对公平的不确定收入,那么基尼系数将逐年稳定下降,其中确定性收入增长率对收入差距的调节作用最强,模拟结果中它能解释基尼系数总减小值的70%以上。
当前我国正处于全面建成小康社会的攻坚阶段,并且要让发展成果惠及更广大民众特别是相对弱势群体,我们需要把蛋糕做大的同时把蛋糕分好,在收入增长的同时,着力进行收入分配调整,使群体之间收入差距逐步缩小。政府有关部门可以从确定性收入和不确定收入的调整入手:采取有效措施提高中低收入群体的基础性和加班工资标准,保证工资性收入的稳定增长;利用个人所得税机制调节不同收入群体的收入再分配;通过市场化手段为不同收入群体创造相对公平的其他多种渠道的收入来源。这些做法都将显著缩小社会总体的收入差距,从而减小基尼系数。本文研究结果为收入分配调整及相关政策的制定和效果的预期提供了理论依据和数据支撑。
[1]徐宽.基尼系数的研究文献在过去八十年是如何拓展的[J].经济学(季刊),2003,(7):757—778.
[2]陈希孺.基尼系数及其估计[J].统计研究,2004,(8):58—60.
[3]陈奇志,陈家鼎.关于洛伦兹曲线和基尼系数的一点注记[J].北京大学学报(自然科学版),2006,(9):613—618.
[4]陈奇志,陈家鼎.关于洛伦茨曲线和基尼系数的统计推断[J].应用数学学报,2011,(5):385—400.
[5]欧阳葵.理论基尼系数及其社会福利含义的讨论[J].统计研究,2011,(5):52—57.
[6]胡祖光.基尼系数理论最佳值及其简易计算公式研究[J].经济研究,2004,(9):60—69.
[7]程永宏.二元经济中城乡混合基尼系数的计算与分解[J].经济研究,2006,(1):109—120.
[8]戴平生.基尼系数的区间估计及其应用[J].统计研究,2013,(1):83—89.
[9]陈建东,罗涛,赵艾凤.收入分布函数在收入不平等研究领域中的应用[J].统计研究,2013,(9):79—86.
[10]周兴,王芳.中国城市与农村基尼系数变动的分解研究[J].经济科学,2010,(1):14—22.
[11]王萍萍.关于我国居民收入基尼系数测算的几个问题[EB/OL].(2013-02-01)[2015-02-17].国家统计局网站.
[12]B.McDonald.Some Generalized Functions for the Size Distribution of Income[J].Econometrica,1984,52(3):647—663.
[13]V.Pareto.La legge della domanda[J].Giornale degli Economisti,1995,(10):59—68.English translation in Rivista di Politica Economica,1997,87(2):691—700.
[14]R.Gibrat.Les Inegalites Economiques[M].Paris:Librairie du Recueil Sirey,1931.
[15]余芳东.国外基尼系数[J].调研世界,2013,(5):57—60.

