函数的概念与性质中易错问题剖析和提醒

■朱 珠

函数的概念与性质比较抽象,初学者常常会犯这样或那样的错误,下面归纳整理剖析并提醒之。

易错点1:混淆复合函数的定义域和外层函数的定义域

剖析:已知复合函数的定义域,求另一个复合函数的定义域,应先求出外层函数f(x)的定义域即为内层函数的值域,再求定义域。

当x∈[-2,1]时,可得x2+1∈[1,5],则f(x)的定义域为[1,5]。由1≤2x+1≤5,可得0≤x≤2,所以函数f(2x+1)的定义域为[0,2]。

提醒:已知函数f[φ(x)]的定义域求外层f(x)的定义域,实质是求φ(x)的值域;已知函数f[φ(x)]的定义域A,求f[g(x)]的定义域,先求出φ(x)的值域B应为外层f(x)的定义域,再利用整体变量观念使g(x)∈B解出x的范围,即为f[g(x)]的定义域。

易错点2:求函数值域时,忽略定义域的限制作用

剖析:上述解法没有考虑函数的定义域,导致所求值域扩大了。由-x2+x+2≥0,

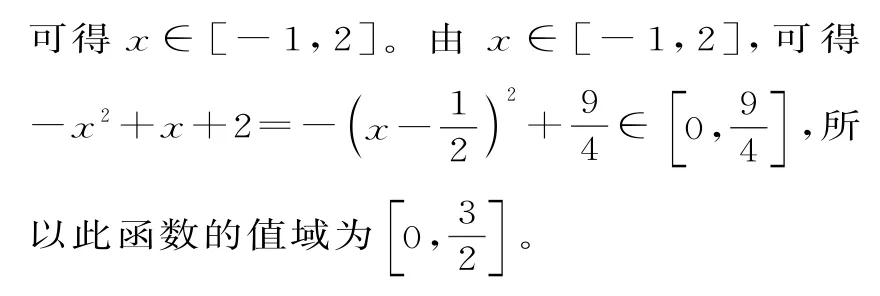
提醒:解决函数值域问题,应从函数的定义域入手,由内到外利用函数在区间上的单调性求解。

易错点3:混淆函数值域为R 与函数定义域为R 的区别

易错点4:混淆单调区间和单调区间子集的意义

例4 若函数f(x)=x2+2(a-1)x+4的单调递减区间是(-∞,4],则实数a的取值范围是_____。

错解:函数f(x)的图像的对称轴为直线x=1-a。函数f(x)在区间(-∞,4]上单调递减,因此1-a≥4,可得a≤-3,即实数a∈(-∞,-3]。

剖析:上述解法把单调区间误认为是在区间上单调了。因为函数的单调递减区间为(-∞,4],且函数图像的对称轴为直线x=1-a,所以1-a=4,可得a=-3。

提醒:单调区间是一个整体概念,如函数的单调递减区间是I,指的是函数递减的最大范围为区间I,而函数在某一区间上单调,则指此区间是相应单调区间的子集。

易错点5:由单调性求参数范围时,忽略整体变量的范围

例5 已知奇函数f(x)是定义在(-2,2)上的减函数,若f(m-1)+f(2m-1)>0,求实数m的取值范围。

提醒:利用函数单调区间求参数的取值范围,一定要让所有的整体变量都在所给区间上,再利用单调性进行转化,最后求交集。

易错点6:分段函数求函数值,忽略整体变量的范围

错解:当1-a>1,1+a<1时,由f(1-a)=f(1+a),可得-1+a-2a=2+2a+a,解得a=-。

提醒:处理分段函数的求值问题,必须考虑自变量的取值所在区间,如果取值不太明确时,要进行分类讨论,同时检验所求自变量的值或范围是否符合题意。

易错点7:奇偶性的判断中,忽视对参数的分类讨论

剖析:上述解法没有对参数进行分类讨论,认为f(-x)≠±f(x)。

当a=0,b≠0 时,f(x)是奇函数;当a≠0,b=0时,f(x)是偶函数;当a=0,b=0时,f(x)既是奇函数又是偶函数;当a≠0,b≠0时,f(x)既不是奇函数也不是偶函数。

提醒:函数定义域关于原点不对称,函数一定是非奇非偶函数。在定义域关于原点对称的前提下,对定义域内任意x都有f(-x)=-f(x),则f(x)为奇函数;对定义域内任意x都有f(-x)=f(x),则f(x)为偶函数;若定义域内存在x0使f(-x0)≠-f(x0),则f(x)不是奇函数;若定义域内存在x0使f(-x0)≠f(x0),则f(x)不是偶函数。