“双减”背景下初中数学优化学生思维的实践探究

文/王萍萍

众所周知，数学思维是一种形式化的思维，是学生学习数学的“工具”。学生运用数学思维，可以通过数形结合，用符号语言表达客观事物。同时，学生不断地发挥数学思维作用，可以顺其自然地提高数学思维能力，提高数学学科核心素养水平。但是，部分教师忽视了学生的主体性，剥夺了学生主动培养数学思维的机会。在这样的情况下，学生会出现思维固化的问题。在固化思维的影响下，学生只能被动接受知识，无法灵活应用，学习效果不尽如人意。对此，在“双减”背景下，教师要关注学生的思维，帮助学生优化思维。

一、提高学生思维积极性

情感是人类思维活动的主要方面[1]。在积极情感的作用下，学生会增强思维积极性，乐于思维。因此，在数学教学中，教师要帮助学生提高思维积极性。

（一）建立良好的师生关系

师生关系是影响教学氛围的因素之一。学生如果畏惧数学教师，在数学课堂上就会缺乏思维的积极性，沉默寡言。在“双减”背景下，教师要利用恰当的方式，与学生建立良好的关系，使学生“亲其师，信其道”，继而积极思维。

例如，在与学生交往的过程中，教师要与学生平等交流。在与学生交流时，教师可以找各种话题，不仅限于学习问题，也可谈论学生感兴趣的轻松话题。多样的话题不但可以使学生产生交流兴趣，畅所欲言，还可以使教师从不同角度了解学生。在了解学生的基础上，教师可以“对症下药”，深入挖掘数学教学资源，选用恰当的数学教学方式，确保数学教学契合学生实际。由此，学生会产生数学学习兴趣，主动走进数学课堂。在数学课堂上，学生可以积极调动思维，踊跃探究数学知识，顺其自然地转变思维方式，发展思维能力。

（二）善于实施赏识评价

赏识评价是帮助学生建立积极情感的重要方式。在学习数学时，大部分学生会遇到各种各样的问题。学生屡屡遭受不同学习问题的打击，便会慢慢失去对数学学习的兴趣，甚至畏惧数学。如此，学生很难产生调动思维的积极性。赏识评价可以让学生发现自己的优点，建立自信心。在自信心的助力下，学生会积极思维，攻克数学学习问题，增强数学学习效果。因此，在数学教学中，教师要善于赏识学生。

以“相似三角形”为例，教师围绕“三角形的相似条件”这一内容设计开放题。

如图1 所示，D、E 分别是△ABC 的边AB、AC上的一点。能否添加一个条件，使△ABC 和△AED相似？

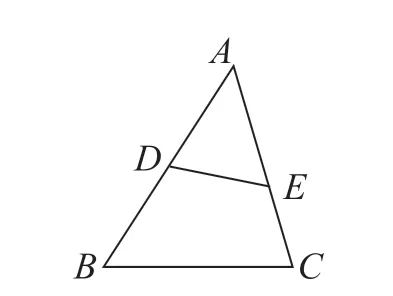
图1

在问题的作用下，大部分学生踊跃思维，联想课堂学习内容，添加条件。此时，部分学生只能想到一个条件，但这也是他们的思维成果，对此教师应及时进行赞赏和鼓励。同时，教师要耐心解析问题，给予他们引导：“△ADE 和△ABC 有一个公共角∠A。根据我们刚才学习的三角形相似的判定定理可以知道，要想使△ABC 和△AED 相似，只要保证什么相等就可以了？”在教师的引导下，学困生积极调动思维，回顾所学，观察图中的三角形，联想到“两个三角形中的另外一组角对应相等”。基于此，学困生写出其他条件。教师赞赏学困生的良好表现，并按照如此方式，继续给予指导。在教师的不断赏识下，学困生产生了思维积极性，开放思维，灵活应用所学，解决了问题。同时，他们也因此掌握了数学知识，发展了思维能力，获得了数学学习满足感，增强了数学学习欲望。

二、进行思维品质训练

思维品质是学生发展思维能力的助力，表现为思维的深刻性、思维的灵活性、思维的创造性等。在数学课堂上，教师要以数学思维表现为重点，结合数学教学内容，进行思维品质训练，促使学生优化思维，发展思维能力。

（一）思维深刻性的训练

思维深刻性表现为深入剖析数学现象或问题本质，发现现象产生的原因和结果，把握数学本质[2]。在数学课堂上，教师要根据数学教学内容，选用适宜的方式，组织思维深刻性训练活动。

数学概念是数学学科的基础内容，反映了客观事物的本质属性。一般情况下，数学概念是经过分析、比较、抽象得到的。这正是进行思维深刻性训练的过程。对此，教师应引导学生经历数学概念的形成过程。例如，在教学反比例函数概念时，教师呈现生活化问题：一辆汽车从南京开往上海（全程大概300 km），全程所用时间t（h）随着速度v（km/h）的变化而变化，能否用含字母v 的代数式表示出t？请根据列出的关系式填写表格：

表1

在问题的作用下，学生积极调动思维，分析问题条件，把握关键信息，同时迁移已有数学认知，列出代数式，并填写表格。之后，教师引导学生分析表格中的数据，思考问题，如“时间t 是速度v 的函数吗？是什么函数？”等。在问题的作用下，学生继续思维，联想函数概念以及不同的函数形式，作出判断。接着，教师呈现与之类似的其他事例，如“一个面积为250 平方厘米的长方形，其长（a）随着宽（b）的变化而变化”“向一个容积为200 立方米的游泳池中注水，注满水所需时间（t）随着注水速度（v）的变化而变化”等。教师鼓励学生列出表达式，并分析、对比共同特征。在此过程中，学生始终保持积极的思维状态，细心观察、对比，发现共同特征，总结反比例函数的概念。

这样的训练不但使学生积极调动思维，逐步探究，借助数学现象抽象出了数学概念，建立了深刻认知，还使学生增强了思维的深刻性，有利于形成良好的思维品质。

（二）思维灵活性的训练

思维灵活性表现为依据具体情况，调整原有思维进程、方向，摆脱制约条件，理解数学本质。观察、联想、转化是学生灵活思维的方式[3]。在数学课堂上，教师要依据教学情况，选择适宜的方式，训练学生思维的灵活性。

以观察为例，这是学生思维的机会。在解决数学问题时，学生认真观察，可以发现关键信息，透过现象看本质，理清解题思路，同时增强思维的灵活性。例如，教师为学生呈现随堂练习题：“解方程（x-1）+1=x”。在解决此问题时，大部分学生迁移数学认知，采用去分母、去括号等方法进行运算，得出结果。但是，这一解题过程并没有体现出思维的灵活性。针对此情况，教师鼓励学生站在整体角度观察。在整体观察时，有学生发现“将右侧的x 移动到左侧和1结合，就可以得到的公因式”，由此轻松地解决了问题。

这种训练不但使学生增强了思维的灵活性，还使学生积累了训练思维灵活性的经验。

（三）思维创造性的训练

思维的创造性表现为打破常规，使用多样方式，分析、解决问题，实现求异、多解[4]。开放性问题是学生发挥创造性思维的基础。在数学课堂上，教师可以依据数学教学内容，或开放问题条件，或开放问题结论，设计开放性问题，驱动学生发挥创造性思维。

以开放问题结论为例，该类开放性问题往往给出问题条件。学生需要分析条件，迁移已有认知，发现规律，得出多样结论。例如，教师为学生呈现开放性题目：如图所示，AB 是⊙O 的直径，BC 是⊙O 的弦，OD与CB 垂直且相交于点E，并与圆相交于点D。请根据已知条件，写出三个不同的正确结论。

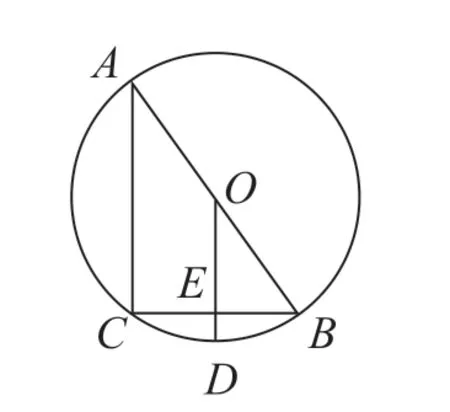
图2

在问题的推动下，学生打破思维定式，对应题目观察图像，同时迁移已有数学认知，得出不同的结论。

这样的训练不仅使学生灵活应用了数学知识，建立了深刻的理解，还使学生增强了思维的创造性，形成良好的思维品质，助推数学学习提质增效。

三、加强思想方法教学

数学思想方法是学生探究数学知识、解决数学问题的有力工具。通过运用数学思想方法，学生可以开拓思维，灵活解决问题，深刻理解数学知识，发展思维能力。在数学教学中，教师要根据教学需要，渗透不同的数学思想方法，助力学生思维发展。

（一）在新知讲解中渗透数学思想方法

新知讲解是数学课堂教学的重要环节，探究数学新知离不开数学思想方法。在数学思想方法的支撑下，学生可以积极思维，深入探究，做到知其然，知其所以然，扎实掌握数学知识，获取数学思想方法，发展思维能力。因此，在新知讲解环节，教师要依据新知内容，渗透适宜的数学思想方法。

以“二次函数y=ax2+k 图像和性质”为例，在新知讲解环节，教师可以布置绘制任务：“请在同一个直角坐标系中绘制出二次函数y=x2，y=x2+1，y=x2-1 的图像。”在此任务的推动下，学生开动思维，迁移已有认知，纷纷使用赋值法，为不同二次函数中的x 赋值，计算出y 的值，由此建立表格。之后，学生根据表格中的数据，在直角坐标系中描点、连线，得到三个不同的二次函数图像。立足学生的成果，教师可布置新的任务：“请大家对比这三个二次函数图像，描述开口方向、顶点、对称轴、最高（低）点、增减性，认真比较，总结它们的共同特征。”在任务的驱动下，学生细心观察，建立表格，认真分析，发现共同特征。接着，教师鼓励学生总结抛物线y=ax2+k 的特点。

这一教学过程渗透了数形结合的思想方法。学生积极思维，绘制图像，观察、分析数量关系，得出结论，扎实地掌握了学习内容和数形结合思想，锻炼了思维能力。

（二）在课堂练习中渗透数学思想方法

课堂练习是学生解决问题的环节。解决数学问题少不了数学思想方法，学生通过应用数学思想方法，可以轻松地获取解题思路和方法，同时锻炼思维能力。所以，在数学课堂练习环节，教师要结合数学教学内容及相应的数学思想方法，设计、呈现练习题。

以“用待定系数法求二次函数的解析式”为例，在学生了解了待定系数法后，教师设计练习题：“已知一个二次函数过点（0，0）（-1，-1）（1，9），求函数解析式。”“有一个二次函数，当x 是0 时，y 是-1；当x是或2 时，y 是0，求函数解析式。”这两个练习题尽管条件以及二次函数解析式不同，但都需要运用函数与方程思想。在解决问题时，学生积极思维，迁移函数与方程思想，分析问题条件，联想二次函数的相关内容，由此列出相应的函数解析式。

如此，学生不但巩固了课堂所学，扎实掌握了函数与方程思想，还切实锻炼了数学思维。

四、结束语

总而言之，培养学生的思维能力，可以使学生在优化思维的同时，扎实掌握数学内容，提高思维水平，实现数学学习的提质减负。因此，在“双减”背景下，教师要关注数学思维对数学学习的影响，将优化学生思维、培养思维能力作为教学重点。在数学教学中，教师要与学生建立良好的关系，善于赏识学生，营造良好的教学环境，调动学生的思维积极性。同时，教师要依据数学教学内容，组织多样的思维训练活动，增强学生思维的深刻性、灵活性、创造性。此外，教师还要渗透数学思想方法，让学生获得思维机会，深入探究数学知识，解决数学问题，发展数学能力。如此，学生可以切实地优化数学思维，提高数学思维能力。