光电效应过程中光电子运动轨迹的模拟
陈永生,史新伟
(郑州大学 物理学院材料物理教育部重点实验室,河南 郑州 450001)
1905年,爱因斯坦提出“光量子”概念,成功阐释了光电效应,并推动了量子理论的发展[1]。通过光电效应实验,可以加深学生对光子模型的理解和对光电效应基本规律的认识,特别是对于金属逸出功、光电子动能和遏止电压间的关系认证。然而,目前使用的光电效应实验装置在实验的准确性和可控性方面仍有很大的局限性[2-4]。由于实验人数多、时间长,造成仪器状态不稳定,测试数据误差大、重复性差等问题。并且由于光电效应实验对实验技术、实验装置要求较高,无法实现学生的自行探索和研究。而模拟仿真实验可以解决实际实验教学中的这些问题,完美展现光电效应现象,提高学生对其规律和本质的认知。
1 实验原理
光电效应实验原理如图1所示。
当一束频率为ν(对应波长为λ)的入射光照射在光电管的阴极金属K上时,金属中的电子会逸出金属,并到达阳极A,形成光电流。根据爱因斯坦光量子理论,光电效应的本质为光子与电子的碰撞-能量作用过程,在碰撞过程中光子把自身的能量传递给电子;电子获得能量后,一部分用于克服金属的束缚(即金属的逸出功W),剩余部分则转变为光电子的动能。整个过程遵循爱因斯坦光电方程:
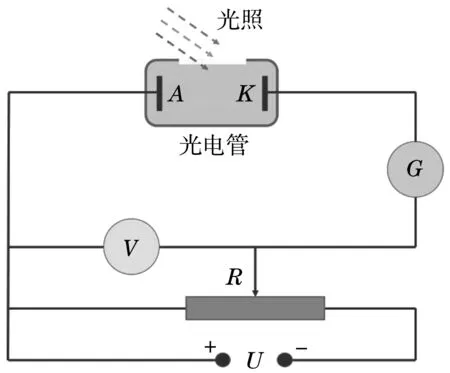
图1 光电效应实验原理图
(1)
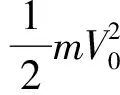
υ0=W/h,
(2)
其中,h为普朗克常数。ν0也称为截止频率。可见,不同的金属因逸出功不同,而具有不同的ν0值。当阴极K和阳极A间加一个正向电压时,光电子受到静电吸引作用而加速向阳极靠拢,光电流增大,并随着电压的增加而达到饱和。当施加一个反向电压时,光电子因静电排斥而速度减小,其动能转变为电势能,光电流降低。当反向电压增至某一个值Us时,光电流降为零,光电子动能等于电势能,即:
(3)
式中:Us称为遏止电压;eUs为电势能。将式(2)、(3)带入式(1)得:
(4)
式(4)为线性方程,Us和ν成正比。实际实验中,通过改变ν,测得对应的Us,再通过作图,根据曲线斜率可求出h值[5]。
2 模拟仿真
模拟仿真的目的是将实验微观现象可视化,提高学生对光电效应本质的认知。仿真采用Comsol软件的粒子追踪模块进行模拟。在模拟过程中,电极间距、阴极发射电流I0、光频率和阳极电压可调。光强度与I0相对应,I0增大,说明光强增大。模块分为静电场和粒子特性设置两部分,前者给出所构筑模型的电场分布,后者设置粒子束的属性和发射方式。图2为光电效应模型结构,为非包围式,且阴极半径(3 mm)大于阳极半径(2 mm),间距为2 cm。默认的入射光波长λ为500 nm,对应的频率ν为6.0×1014Hz,阴极发射电流I0为1nA,金属的逸出功W为1.5 eV。
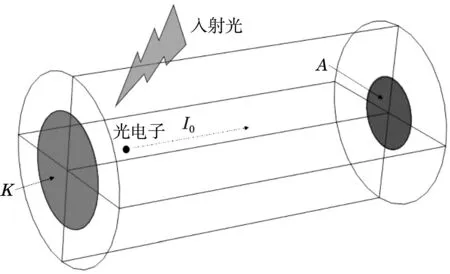
图2 光电效应模型结构
3 结果与讨论
图3为不同阳极电压下的电场分布情况。可以发现,电场主要集中于阳极附近,而阴极附近的电场很弱。这说明光电子距离阳极越近,受到电场的作用越强。
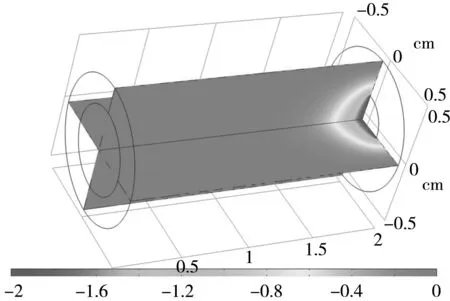
(b)-2 V
图4为在不同阳极电压下光电子的运动轨迹及其相对速度的变化。当阳极电压为0 V时,光电子呈直线运动,且在运动过程中速度不变,为V0。同时,由于阳极半径较小,只能接收部分光电子。当阳极施加2 V电压时,光电子在距离阳极0.5 cm时运动速度开始迅速增加,并向阳极靠拢,使光电流增大。而当阳极电压设置为-2 V时,光电子在阳极附近运动速度降低,并向阳极周围分散,甚至出现反弹。这说明电子的动能转变为电势能,使光电子速度减小,阳极接收的光电子数目减小,光电流降低。从图4可以非常直观地观察到不同阳极电压下光电子的运动特性。

(a) 0 V
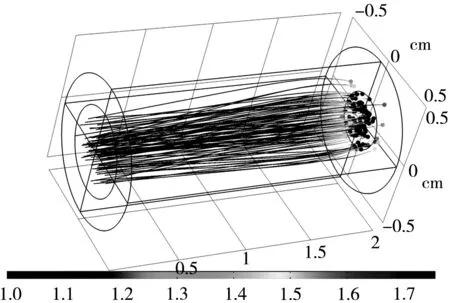
(b) 2 V
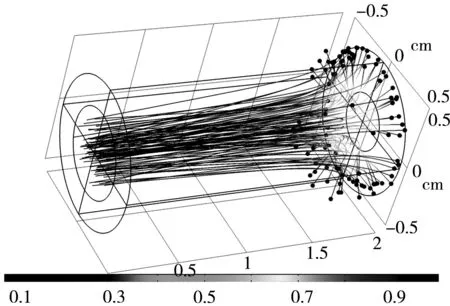
(c)-2 V
图5为阳极电压分别为0、2和5 V,阴极发射电流为1nA时,阳极光电流随时间的变化。可以发现,当未施加阳极电压(阳极电压为0 V)时,光电子离开阴极后于~34 ns到达阳极产生阳极电流(电流为负值说明电流方向与光电子运动方向相反);随后,阳极光电流在2~3 ns内迅速达到饱和,整个过程非常短暂,很好地反映了光电效应的瞬时性。但阳极饱和光电流显著低于阴极发射电流,说明有很大一部分光电子未被阳极收集。当阳极施加正向电压后,光电子受到电场的加速作用,动能增加,速度增大,使得到达阳极的时间缩短,且电压越高,时间越短。同时,光电子受到阳极的静电吸引能力增强,向阳极靠拢而使阳极饱和光电流增大,如图5(b)所示。特别是当电压为5 V时,阳极饱和光电流与阴极发射电流相当。
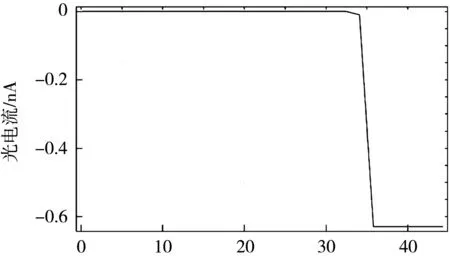
(a) 0 V时间/ns
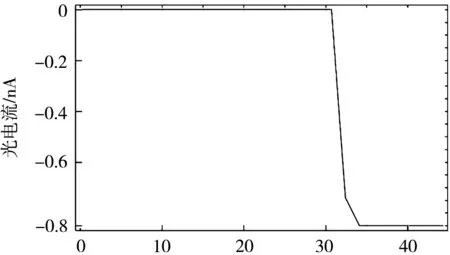
(b) 2 V时间/ns
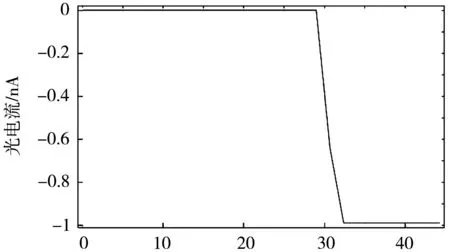
(c) 5 V时间/ns
图6为阴极发射电流分别为1 nA和3 nA时,阳极光电流随阳极电压的变化。
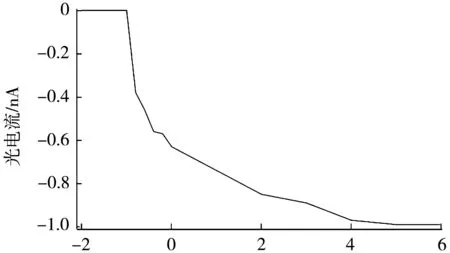
(a) 1 nA阳极电压/V
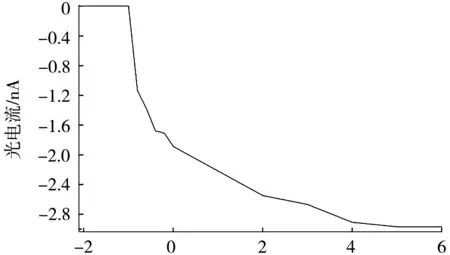
(b) 3 nA阳极电压/V
当阳极施加正向电压时,光电流随着电压的增加而增大;当电压为5 V时,阳极光电流达到饱和。当阳极施加反向电压时,随着电压的增加,光电子受到阳极电场的排斥作用增强,动能转变为电势能,使光电子的速度降低,阳极接收到的光电子数目降低,如图4(c)所示,光电流减小;当电压为-1 V时,光电流为0,说明这时光电子吸收500 nm波长的光子的能量后获得的动能与-1 V电压的电势能正好相等(见式(3)),得出遏止电压Us为-1 V,与理论计算值0.98 V非常吻合(误差与电压扫描间隔(0.2 V)较大造成)。同时,随着阴极发射电流的增加,阳极饱和光电流增大,即饱和光电流和入射光强成正比。这是因为当入射光的频率一定时,入射光的强度影响光电子数目,光强越大,光电子的数目就越多,光电流也越大[6-7]。但是遏止电压Us值不变,说明其与光强无关。
图7为入射光波长为600 nm时的阳极光电流与阳极电压关系曲线。
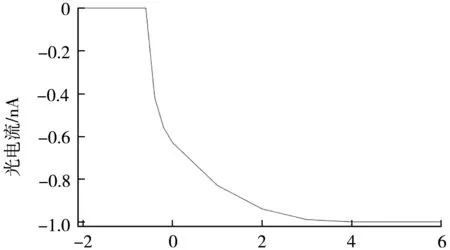
阳极电压/V
相同的阴极发射电流下,饱和光电流对应的电压减小至3 V,遏止电压Us降为-0.6 V。这说明遏止电压Us与光电子的初动能成正比,即与入射光的频率呈正比,如式(4)所示。
4 结 论
模拟仿真实验排除了实际仪器和操作过程中的不利影响,将实验现象直观化和重复化,利于学生进行深入的思考和探索。通过对光电子运动轨迹的模拟,并将该微观过程可视化,增强学生对阴极功函数、光频率、阳极电压和电子动能间的关系的认知。通过阳极光电流与阳极电压和阴极发射电流的关系,遏止电压与入射光波长的关系,完美地解释了光电效应实验规律,增强了学生对光电效应现象及其本质的理解和认识。

