《崇祯历书》南极增星溯源研究

吉 翔

(中国科学院大学人文学院,北京 100049)

明末,为改革天文历法,徐光启等人组织编纂了大型历算丛书《崇祯历书》,这是中国历史上首次大规模系统地引进欧洲天文学。《崇祯历书》中包含有《恒星经纬图说》一卷和《恒星经纬表》二卷,这两部分分别以图和表的形式展示了全天星空,其中包括南极附近126颗新增恒星的坐标位置(1)《恒星经纬表》中有坐标数据的为126颗,《恒星经纬图》中则多于这一数目,详见表1的统计数据。,可以说是首次系统准确地将这部分南极增星介绍到中国。目前学界关于《崇祯历书》中南天星图和星表的来源的认识仍不清晰。本文重新梳理了《崇祯历书》中南天星图和星表之间的关系,对南极增星进行了重新证认,在此基础上考查了《崇祯历书》中南天星图与星表和豪特曼(Frederick de Houtman, 1571—1627)星表、鲁道夫星表与巴耶尔(拜耳,Johann Bayer, 1572—1625)星图等的关系。我们认为,《崇祯历书》中南天星的直接来源应为格林伯格(Christoph Grienberger, 1561—1636)星表与巴耶尔星图,最初的观测则是由喜帕恰斯(Hipparchus,前190—前120)与凯泽(Pieter Dirkszoon Keyser, 1540—1596)完成。进而,我们还考察了巴耶尔星图和豪特曼星表与鲁道夫星表之间的关系,绘制出一幅南极增星部分早期来源间的关系图。

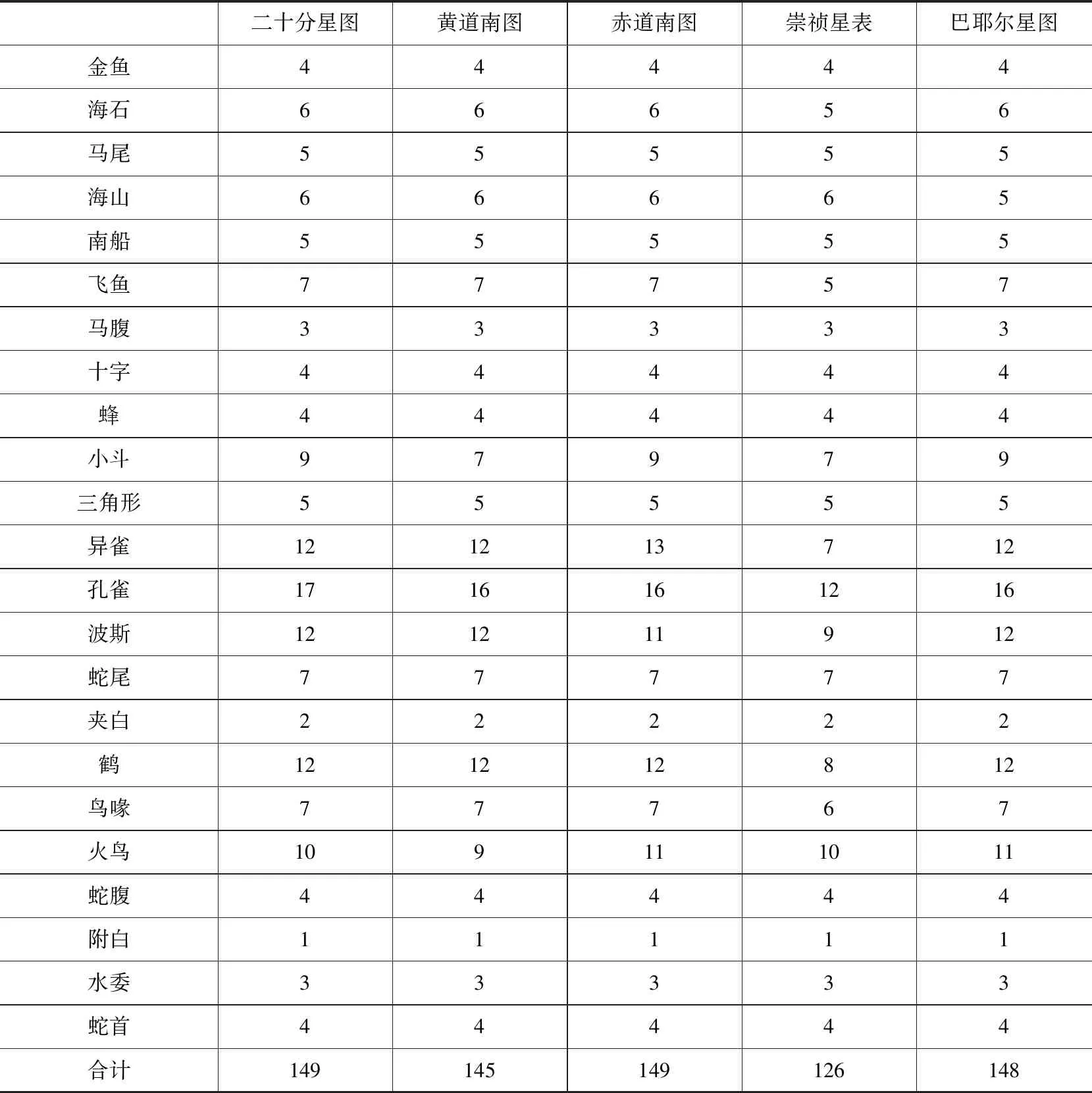
表1 《崇祯历书》星图与星表与巴耶尔星图包含恒星数量的比对(巴耶尔星图如下文图7重新划分天区后)

1 可能的来源

《崇祯历书》于崇祯二年(1629)九月开始组织编修,于崇祯七年(1634)十一月完成,崇祯四年(1631)八月初一日徐光启(1562—1633)第二次进呈历书时已完成《恒星经纬表》与《恒星经纬图说》部分([1],页10)。徐光启在《恒星经纬图说》的前言中提到,“南总图自见界诸星而外,尚有南极旁隐界诸星,旧图未载此,虽各省直未见,从海道至满剌加国悉见之……惟是向来无象无名,故以原名翻译附焉”,“所有诸星皆在恒隐界中,旧传所无,今译名增入,是为南极分图也”([1],页495、497),明确指出南极附近新增的这部分恒星的名称是翻译而来。

关于《崇祯历书》中南天星图和星表来源的研究前人已做过不少工作:潘鼐先生认为《崇祯历书》南天星图来源于豪特曼星表[2],但他的论证缺少基于星表数据的具体分析。孙小淳老师认为《崇祯历书》中南天增星的精度不高,偏差超过1度的情况很多,是传教士来华途中测量的可能性极大,也有可能受到了巴耶尔星图的影响[3]。孙老师在另一篇文章中以耶鲁亮星星表为标准计算了在赤道坐标系下各个星表的精度,发现豪特曼星表最为精确,鲁道夫星表比《崇祯历书》中的星表稍为精确[4]。但孙老师的这两篇文章并未论证南极增星的黄赤道坐标数据存在转换关系和给出恒星的具体证认情况。本文将给出具体的证明和证认情况,并使用一手观测数据的黄道坐标数据对精度进行重新计算。丁敏等将《崇祯历书》恒星经纬表中的数据进行了模拟绘图比对,认为星表里有记录的星,确实是严格按照坐标数据,采用球极投影、垂直透视投影和正弦投影等方法画到图中的,据表绘图之说成立[5]。但此文仅讨论了每个星官的局部比对情况,我们将以整个南半球的比对情况来进一步说明图表数据之间的一致性。F. Verbunt与R. H. van Gent等将部分西方星表如托勒密(100—168)星表、第谷星表、豪特曼星表、鲁道夫星表与哈雷星表等进行了数字化处理,证认了其中的部分恒星,并讨论了星表数据的精度[6]。Elly Dekker研究了凯泽与豪特曼的观测数据在天球仪和星图上的使用与演变情况[7],基于此我们绘制了南极增星部分早期来源间的关系图。慧泽霖在北堂图书馆中找到过巴耶尔星图[8],北堂藏书中也包含格林伯格星表[3]与鲁道夫星表[9]等,这些都为我们进一步探索《崇祯历书》南极增星的源头提供了基础。

《崇祯历书》中南天星表的来源有如下几种可能:(1)凯泽与豪特曼第一次航行的观测数据(1595—1597)(2)第一次航行的主要观测可能由凯泽完成,豪特曼做出了怎样的贡献仍存在争议(参见参考文献[10])。凯泽的手稿已失传,可以对普朗修斯(Petrus Plancius,1552—1622),洪第乌斯(Jodocus Hondius,1563—1612)和布劳(Willem Janszoon Blaeu,1571—1638)等人的天球仪进行考查,此外巴耶尔星图也可能是从洪第乌斯的天球仪上测量而来(参见参考文献[7])。;(2)豪特曼第二次航行的改进星表(1603)(附表中简称“豪表”);(3)鲁道夫星表南天部分(1627)(附表中简称“鲁表”);(4)巴耶尔星图(1603)(附表简称“巴耶尔”);(5)传教士来华途中自测。我们将对这些可能进行论证。

2 南极附近恒星图、表关系及恒星证认

首先,对《恒星经纬图说》与《恒星经纬表》之间的关系进行考察。《恒星经纬图说》的前言有云:“绘图、立表、测天三事悉皆符合”,“且一星一表,毫发难移,点缀既毕,自然肖象非若书绘之家先想成形而追形定位,虽欲更移秒末以就成体势,固不可得也”[10]。《恒星历指》也提到“图中各星所在度分,与立成表所载本星度分,各各符同,全无差失”,即《恒星经纬图说》与《恒星经纬表》应是完全对应的等价关系。丁敏在考查图和表之间关系时仅对单个的星官进行了局部的比对[5]。我们对整个南天星图与星表间的关系进行了比照(图1),可以看出,尽管有一些偏差,但总体对应良好,星表中的星,确实是严格按照坐标数据,采用正确的方法画到星图中的,整体上可以认为是据表绘图,因此我们认为图表同源,而无需对图和表的数据来源分别考查。此外,从叠加图中也可以看出星图中的星数要多于星表。

图1 星图与模拟绘制星图叠加图①

进而对《恒星经纬表》中黄道坐标与赤道坐标之间的关系进行讨论。若存在转换关系,则无需对黄道坐标数据与赤道坐标数据的来源分别考察。《崇祯历书·恒星历指》卷中有“以恒星赤道经纬度求其黄道经纬度第五”与“以恒星之黄道经纬度求其赤道经纬度第一”,这表明编制者们已经掌握了黄赤道坐标数据之间相互转换的方法。《恒星经纬表》中同时给出了恒星的黄道坐标数据和赤道坐标数据,它们之间可能存在转换关系。Jacob Kistemaker与孙小淳等认为《崇祯历书》南极增星的赤道坐标是由黄道坐标转换而来[4]。张兆鑫也认为《崇祯历书》中南极增星的赤道坐标数据不是源自实际观测,而是由其黄道坐标数据推算得到的[11]。但他们都没有给出具体的证明,我们在这里作简单证明。

《崇祯历书》中取黄赤交角值为23°31′30″,这是采用的第谷(Tycho Brahe,1546—1601)的观测数值。我们可以采用这一黄赤交角值进行直接换算,看是否存在转换关系。在这里我们采用一种更为简便的方法:以λ和β代表黄经和黄纬,α和δ代表赤经和赤纬,则在黄赤道坐标数据进行相互转换时必须满足cosλcosβ=cosαcosδ,只需验证是否普遍存在cosλcosβ=cosαcosδ这一等式关系即可初步验证黄赤道坐标数据之间是否存在转换关系。我们取k=cosλcosβ/cosαcosδ,计算结果可以在文末附表中查询,高达2/3的恒星的k值落在0.99到1.01之间(4)作为对比,我们选取《崇祯历书》中的黄道坐标数据与豪特曼星表中的赤道坐标数据计算了k1,《崇祯历书》中的赤道坐标数据与鲁道夫星表中的黄道坐标数据计算了k2,落在0.99到1.01之间的比例均远小于2/3。,考虑到换算时的误差,我们认为黄赤道坐标数据之间普遍存在换算关系。小斗五的k值超过200,呈现明显异常,这其实不是反例。星表中小斗五的赤纬数值为89°57′,但在赤道南图中小斗五却并不在南天极附近,经计算检验可以发现崇祯星表中小斗五的赤道坐标数值是错误的。

而对尾数分布的统计可以进一步证明黄赤道坐标数据之间存在换算关系,并且是由黄道坐标数据推得赤道坐标数据。以金鱼一的黄经36°23′这一数值为例,我们取其分的数值23的尾数3,定义3为36°23′的尾数。对于测量足够精确的星表,如《崇祯历书》之后半个世纪的哈雷南天星表,由于使用了望远镜而使得精度大为提高,恒星坐标的尾数大致呈现均匀分布。但《崇祯历书》星表以及在此之前的星表由于测量不够精确,作了大量的取整或者取中间值等的近似,尾数的分布一般会对0和5呈现明显的偏好。对文末附表中各列数据的尾数分布进行统计和分析,结果如下(表2):

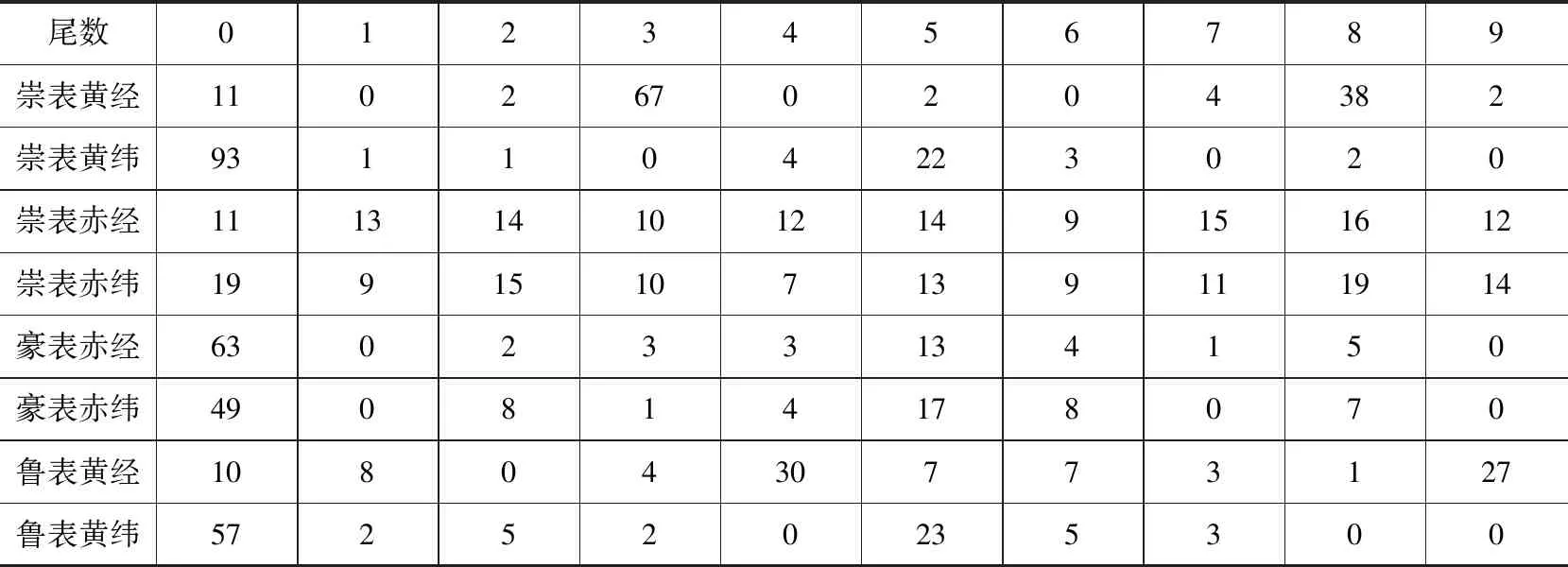
表2 《崇祯历书》、豪特曼星表与鲁道夫星表部分南天恒星黄经尾数统计

我们发现,豪特曼星表数据的尾数分布在0和5上较高,尤以0上最高,类似的现象出现在崇祯星表的黄纬和鲁道夫星表的黄纬数值上,而崇祯星表和鲁道夫星表的黄经数据的尾数则分别发生了3分和4分(或者是9分)的偏移。由于地轴进动导致春分点的西移,在黄道坐标系中,恒星的黄经发生约每年50秒的持续变化,黄纬的变化则非常微小。所以崇祯星表与鲁道夫星表应当是由于历元的变化对黄经数据进行过处理。崇祯星表赤道坐标数据的尾数则大致呈均匀分布,这证明黄道坐标为实测的一手数据,赤道坐标数据不是出自实测,而是由黄道坐标数据换算而来。

《崇祯历书》星表选定的历元是1628年天正冬至。3分的黄经修正大约对应3.6年,考虑到计算过程中的四舍五入,则大约为3至4.2年。当然修正值也可能是13分、23分、33分或者更高。我们进一步考查崇祯星表中黄经数值的分的数值,发现在67个尾数是3的数据中,有11个为3分,4个为13分,25个为23分,5个为33分,10个为43分,12个为53分,23分的个数遥遥领先,这似乎表明崇祯星表的黄经数值可能来自某个非常不准确的来源,不少恒星的黄经数值只精确到度,经过历元换算后才带上了23分。如果这一猜测是正确的话,23分对应27—28.2年的修正,即数据来源的历元应当落在1600—1601年。下面我们将会论证这一猜测的合理性。

鲁道夫星表的历元是1601年,如果是4分的修正则大约对应4.8年,考虑到四舍五入,则观测时间应回溯4.2—5.4年,恰好对应了凯泽等人第一次航行的时间(1595—1597),开普勒(Johannes Kepler,1571—1630)在这份星表的前言部分确曾提到了凯泽的名字,似乎暗示鲁道夫南天星表中的部分恒星可能源于凯泽的观测。

对于恒星星名中西对应的探索,前人做过充分的工作。常福元(1874—1939)编写的《中西对照恒星录》(1920)主要基于《清会典》而成;伊世同(1931—2008)编著的《中西对照恒星图表》(1981)则主要参考了《仪象考成》与《仪象考成续编》。据察,《仪象考成》中的南极增星来自1679年发布的哈雷南天星表[12],《崇祯历书》中的南极增星有着不同来源,有必要进行重新证认。本文对南天恒星的证认数据来源于《崇祯历书附西洋新法历书增刊十种》,豪特曼星表与鲁道夫星表数据则基于F. Verbunt与R. H. van Gent的工作[6]。由于正文篇幅所限,具体的证认结果见文末附表。

3 溯源分析

豪特曼星表是豪特曼在第二次远征东印度的航行之后于1603年发表的。对尾数的分析表明,《崇祯历书》中南天增星的数据源头应当采用黄道坐标系,而豪特曼星表采用的是赤道坐标系。在附表中我们对恒星进行证认,发现大多数星官中均存在一些恒星无法与豪特曼星表相对应的情况。

我们将豪特曼星表中的赤道坐标数据转换成了黄道坐标数据,用《崇祯历书》南天星表中的恒星的黄经与豪特曼星表中恒星的黄经的差值Δλ作X轴,黄纬的差值Δβ作Y轴,绘制二维坐标散点图(图2):

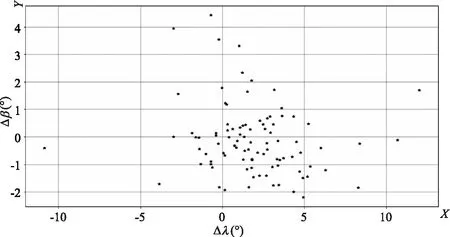
图2 《崇祯历书》南极增星与豪特曼星表的黄经差-黄纬差散点图①

由图可见,Δλ与Δβ大致为随机分布,这表明《崇祯历书》中的星图和星表与豪特曼星表不存在明显继承关系。

鲁道夫星历表于1627年出版。在鲁道夫星表与《崇祯历书》之间这28年间,恒星黄经的变化大约为23分,而黄纬的变化则只有10秒左右(6)恒星位置随时间的变化还应考虑到恒星的自行,但恒星的自行直到1718年才由哈雷(Edmond Halley,1656—1742)发现,因此本文中无需考虑。。我们用《崇祯历书》南天星表中的恒星的黄经与鲁道夫星表中恒星的黄经的差值Δλ作X轴,黄纬的差值Δβ作Y轴,绘制二维坐标散点图(图3)。如果《崇祯历书》中部分恒星来自鲁道夫星表,应当预期的是这部分恒星会出现在点(1/3,0)附近。

图3 《崇祯历书》与鲁道夫星表的南极附近增星黄经差-黄纬差散点图②

可见,在X=1/3这条线上有几颗恒星一字排开。这些恒星包括十字一、十字二、十字三、十字四、马腹一、马腹二、马腹三、马尾一和小斗二。其中十字和马腹星官均有多颗星集中出现在这里,这应当不是偶然。我们还注意到,除了小斗二之外,这些恒星在《崇祯历书》星表中的尾数均为0,这意味着可能没有经过历元的换算,存在几种可能:一是这部分星是传教士来华途中新测;二是可能不知道这部分星的具体观测年份;三是观测年代过于久远以至于无需考虑这20多年的黄经误差。进而,我们将《崇祯历书》中所有尾数为0的星与托勒密星表进行比对,发现十字一、十字二、十字三、十字四、马腹一、马腹二、马腹三、马尾一和马尾二这9颗星的数据全部源自托勒密星表,在托勒密星表的基础上,黄经统一增加21度20分(其中马尾二出现计算或传抄错误,只增加21度10分),黄纬保持不变或者稍作变化。类似的现象也出现在了鲁道夫星表中,鲁道夫星表中这9颗星也是来自托勒密星表,黄经增加21度,黄纬几乎不变。

利用公式cosθ=sinβ1sinβ2+cosβ1cosβ2cos(λ1-λ2)计算同一颗恒星在《崇祯历书》星表中的位置和鲁道夫星表中位置的角距离,可以看出角距离θ与黄经λ和黄纬β之间的关系(图4)。结合上文对《崇祯历书》星表历元换算的讨论和下文对巴耶尔星图和格林伯格等的考查,我们可以看到《崇祯历书》中的星表对黄经值进行过23分的换算,因而我们将在数据处理中将《崇祯历书》中的黄经值减去23分。

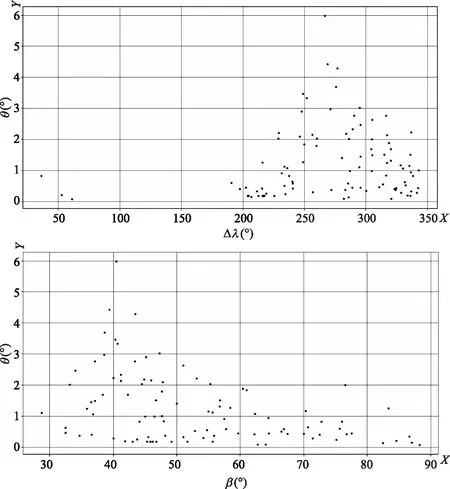
图4 (被证认为)同一颗恒星在《崇祯历书》星表与鲁道夫星表中位置的角距离与黄经和黄纬间的关系图①

由图4可见,角距离θ似乎与黄经λ和黄纬β均存在一定的关系,集中表现在黄经270度处两个星表的角距离差值达到峰值,且越向低黄纬地区,两个星表的角距离平均差值越大。我们发现角距离θ最大的10颗星全部来自孔雀和三角形星官,这似乎表明孔雀星官和三角形星官中的部分恒星在《崇祯历书》星表与鲁道夫星表中有不同的来源,如果将这10颗星剔除掉,角距离θ与黄经λ和黄纬β之间的相关性显著减弱了。

《崇祯历书》星表中的数据与鲁道夫星表中的数据尽管不相同,却可能存在一定的关联,其中一个星表中的黄经数据可能出现了某种系统性误差。下面我们将考查两个星表的精度。我们依据现代的依巴谷星表(附表中简称“依表”)的数据计算出了所有恒星在J1600历元下的黄道坐标数据,分别绘制两个星表与理论值之间的Δλ-Δβ图并计算角距离(图5)。

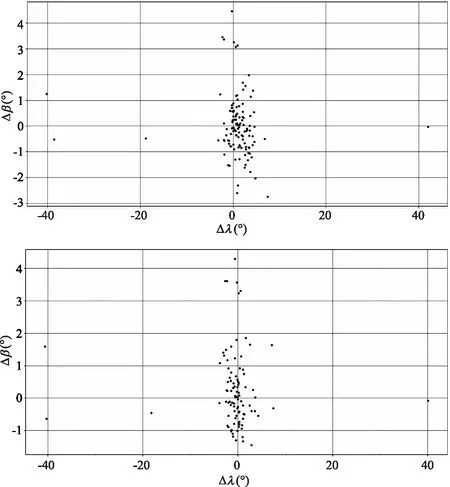
图5 《崇祯历书》星表与鲁道夫星表相对于现代计算值的黄经差-黄纬差散点图①

由图5可见,《崇祯历书》星表的黄经数据存在整体向右略微偏移的情况。此外两个星表中各有4颗星的黄经偏差超过10度,主要是由于这些星均处于高黄纬地区,观测时很小的角距离偏差就会造成较大的黄经偏差。两图中的4颗星均为夹白二、夹白三、金鱼三和金鱼四,它们在两张图中位置分布也基本一致,表明《崇祯历书》星表与鲁道夫星表中的这4颗星极有可能是同源的。

另外,通过计算两个星表中所有星相对于现代计算值的角距离偏差,我们发现《崇祯历书》星表的偏差均值为1.417°,鲁道夫星表为1.281°,在角距离平均偏差值这一维度,鲁道夫星表要比《崇祯历书》星表的精度略高。存在两种可能:一是鲁道夫星表对部分恒星的数据进行了某种修正,二是鲁道夫星表相比《崇祯历书》多出另一个精度更高的源头,Elly Dekker的研究支持了后一种可能[7]。

实际上,邓玉函(Johann Schreck,1576—1630)曾向伽利略(Galileo Galilei,1564—1642)求教精确计算日食的方法,在伽利略因与教会间的矛盾拒绝后,邓玉函后又求助于开普勒[13],但邓玉函没有等到开普勒的回复便去世了,直到1645年,传教士卜弥格(Michal Piotr Boym,1612—1659)带着一份鲁道夫星表来到中国,这份鲁道夫星表后来被送到北京[9]。因此《崇祯历书》中的星图与星表应当没有参考鲁道夫星表,但两个星表中的十字一、十字二、十字三、十字四、马腹一、马腹二、马腹三、马尾一和马尾二这9颗星的数据源自托勒密星表,夹白二、夹白三、金鱼三和金鱼四这4颗星也大概率同源。部分恒星的同源关系可能是通过巴耶尔星图建立的。

巴耶尔星图系由德国天文学家巴耶尔编著,于1603年在今天德国的奥格斯堡出版,包含51张星图。其中的第49张星图是航海十二星座,第40张星图是南船座,第41张星图是半人马座,第51张是黄道南图。

在将《崇祯历书》中的黄道南图与巴耶尔星图中的黄道南图叠加后,我们发现二者非常相似但偏差不小,考虑到两张星图的投影可能均存在误差,误差累积后会造成较大偏差,我们将巴耶尔星图中的黄道南图与程序模拟的《崇祯历书》黄道南图叠加,结果如下(图6):

图6 巴耶尔星图黄道南图与程序模拟《崇祯历书》黄道南图叠加图①

可以看到中心部分几乎完全一致,这表明《崇祯历书》中23个南极星官中的大多数可以与巴耶尔星图的黄道南图对应,一些距离黄极较远的星官如波斯、火鸟等,虽然不吻合,但形状相似,可能是巴耶尔星图在投影时出现了偏差。

进而,我们发现《崇祯历书》南天星图和星表与巴耶尔星图存在更多的一致性。我们依据《崇祯历书》中星官所占天区的范围对巴耶尔星图进行了重新划分,航海十二星座的划分如下(图7):

图7 依据《崇祯历书》中星官对天区的划分方式对巴耶尔星图进行重新划分图①

由于《崇祯历书》中的星图和星表所包含的信息量不同,我们统计了每个星官在星图与星表中的星数,并且与巴耶尔星图中的星数比对(表1)。可见,《崇祯历书》中星图中的星数与巴耶尔星图中的星数存在高度的一致性,而星表则对星数较多的星官进行了精简。

参考Ian Ridpath对巴耶尔星图的证认[15],我们将《崇祯历书》中新增的23个南极星官中的恒星与巴耶尔星图进行比对,发现《崇祯历书》星表中126颗恒星中的125颗都可以在巴耶尔星图的第40、41或者第49张图中找到。《崇祯历书》星图中每个星官的信息含量大多不超出巴耶尔星图,除了海山和孔雀。黄道二十分星图中孔雀星官中多出来的一颗星可能是多余的误点,因为这颗星在黄道南图和赤道南图中均不可见。对于海山星官中多出的海山四,我们考查大量星图星表和天球仪后发现仅在《崇祯历书》中可见。注意到此时崇祯星表中黄经尾数为0的11颗星中有9颗已经可被认为源自托勒密星表,将剩余的两颗星海山四与火鸟五的黄经坐标减去21度20分后到托勒密星表中检索,找到了海山四的对应星,且黄纬数值一致。由于F. Verbunt与R. H. van Gent在对鲁道夫星表进行证认时将一颗原本应当证认为HIP57439的恒星误证认为HIP59747[7],使得我们先前没有发现海山四也是源自托勒密星表。火鸟五则未找到,可能是《崇祯历书》星表的编制者忘记对其进行黄经换算所致。至此,《崇祯历书》星表中的所有恒星均可以在托勒密星表或者巴耶尔星图中找到,且《崇祯历书》中南天星图中每个星官中恒星数量几乎与重新划分后的巴耶尔星图对应。

巴耶尔星图中的第49张航海十二星座图中同时绘有黄道和赤道坐标系,但投影方式出现了错误,其中应当有一个坐标系的经线为弧线,考虑到直接测量出来的数据可能不太准确,我们可以利用其中的黄经和黄纬辅助线来加以考查。举例来说,我们注意到其中的小斗二和小斗三几乎完全落在240度黄经线上,夹白三几乎完全落在300度黄经线上,可以到《崇祯历书》星表中反查,发现小斗二和小斗三的黄经数值为240°23′,夹白三为300°23′,如果黄经数值确实进行过23分的历元换算,则完全匹配。再以孔雀星官为例,从巴耶尔星图中读出的黄经数值孔雀一和孔雀二应当小于270度,孔雀三和孔雀四应当大于270度,这与《崇祯历书》星表相符,而与鲁道夫星表不符。通过对恰好落在坐标线上的恒星以及恒星相对于坐标辅助线位置的考查,发现《崇祯历书》星表中的数值几乎与巴耶尔星图完全一致,而鲁道夫星表与巴耶尔星图之间则存在很多矛盾。

Elly Dekker认为巴耶尔星图中的航海十二星座数据测量自洪第乌斯制作于1600年或1601年的天球仪[12]。我们将巴耶尔星图与之进行比对后发现,对于航海十二星座以外的部分,巴耶尔星图中水委、海石、海山、南船等星官相对应的天区,也与洪第乌斯的天球仪基本一致,十字和马尾星官所在的天区则有明显的不同。巴耶尔星图中马尾星官所对应的天区比洪第乌斯的天球仪多出两颗星,这两颗星的来源我们仍不清楚。巴耶尔星图中的南十字相对于210度黄经线的相对位置与洪第乌斯天球仪中的南十字相对于180度赤经线一致,起初我们以为是巴耶尔在对天球仪进行测量时误将180度赤经线当成210度黄经线,但在对鲁道夫星表中的南十字考查之后,我们发现巴耶尔星图中的南十字同样与托勒密星表中的数据相吻合。在绘制出了新的航海十二星座的情况下,巴耶尔星图中半人马座的南十字依然保留了托勒密星表中的数据。这种对新旧数据的取舍与调和的方式与《崇祯历书》星表和鲁道夫星表相同,而与豪特曼星表、普朗修斯、洪第乌斯和布劳等人的天球仪不同。

通过对叠加图、星数的一致性、信息含量和位于辅助线上的特定恒星与南十字座的考查,我们发现《崇祯历书》星表与巴耶尔星图存在高度一致性。《崇祯历书》是否有可能直接参考了天球仪?我们进行比对后发现相比洪第乌斯1600年的天球仪,巴耶尔星图在信息上有所损失,在蝘蜓座少了一颗星,在剑鱼座与水蛇座也少了一颗星,而这些缺少的星也未出现在《崇祯历书》星图与星表中,因此《崇祯历书》中的星图与星表应当不是直接来自洪第乌斯的天球仪或更早期的来源。除去来自托勒密星表的10颗星外,巴耶尔星图应当是《崇祯历书》南天星图与星表的直接来源。慧泽霖在北堂图书馆中找到过巴耶尔星图,也可以作为佐证[8]。

《崇祯历书》中星图星表的直接来源应当为托勒密星表与巴耶尔星图,那么这些恒星的数据最初又是源自哪里?十字一、十字二、十字三、十字四、马腹一、马腹二、马腹三、马尾一、马尾二和海山四这10颗星直接来自托勒密星表。但托勒密星表有一些衍生星表,比如格林伯格星表[16]中的克拉维斯星,便是由托勒密星表换算而来。我们将这10颗星在不同星表中的数据汇总如下(表3):

表3 10颗同源恒星在《崇祯历书》星表、鲁道夫星表、格林伯格星表与托勒密星表中的坐标

可以看到相对于托勒密星表的原始数据,鲁道夫星表黄经增加21°,黄纬均小幅度增加。而《崇祯历书》星表中黄经增加21°20′,黄纬则大多保持不变,其中十字二的黄纬51°01′应当是传抄错误,十字四的黄纬55°40′可能是来自格林伯格星表,黄经则是在格林伯格星表的基础上加23′。因此,这部分恒星数据的直接来源应当是格林伯格星表,尽管数据仍是从托勒密星表换算而来。北堂藏书中包含格林伯格星表[3],也可以作为佐证。R. R. Newton,Dennis Rawlins,Gerd Grasshoff[17],Keith Pickering与Dennis Duke[18]等的研究表明托勒密星表几乎完全出自喜帕恰斯的星表。因此这部分恒星的数据可能出自喜帕恰斯于公元前2世纪的观测。

对于十字星官,《崇祯历书》中将十字架一的星等记为4等,这一点与格林伯格星表和托勒密星表相符合。考虑到十字架一的星等和十字星官的形状,我们将《崇祯历书》中的十字星官证认为HIP63003、HIP61084、HIP62434与HIP60260,有关十字架四,F. Verbunt与R. H. van Gent的文章[6]曾在HIP60260与HIP60718之间有过犹豫,基于位置应当为HIP60260,基于亮度应当为HIP60718。但可以肯定的是,将十字架一证认为HIP63003,表明《崇祯历书》中的十字星官与我们今天所认为的南十字不同。基于星等和位置的考查同样表明巴耶尔星图中的十字与我们今天所认为的南十字也不完全对应。

对于航海十二星座所对应的金鱼、飞鱼、蜂、小斗、三角形、异雀、孔雀、波斯、蛇尾、夹白、鹤、鸟喙、火鸟、蛇腹、附白、蛇首这16个星官,脉络同样清晰,Elly Dekker认为巴耶尔星图中的航海十二星座测量自洪第乌斯的天球仪[7],洪第乌斯的天球仪上航海十二星座的数据源于凯泽第一次远征东印度的观测。

水委星官中的两颗位于航海十二星座凤凰座,而普朗修斯与洪第乌斯在1598年的天球仪上表明水委一也是由凯泽观测,因此水委星官同样也源于凯泽第一次远征东印度的观测。

对于海石、海山、南船这三个星官中的16颗星,除已经被证明来自托勒密星表的海山四以外,在范朗伦(Jacob Floris van Langren,1525—1610)1589年的天球仪、莫利纽克斯(Emery Molyneux,?—1598)1592年的天球仪和普朗修斯1594年的Orbis Terrarum上均不可见,似乎是与航海十二星座一起首次出现在普朗修斯与洪第乌斯1598年的天球仪上,这些星有可能也是出自凯泽的观测。

此时剩余的星还包括马尾三、马尾四和马尾五。马尾五可以在洪第乌斯的天球仪上见到,应当也是源自凯泽的观测,马尾三和马尾四的数据源头我们仍不清楚。这两颗星在我们所考查的所有1603年之前的星图星表与天球仪中均不存在,尽管同样发表于1603年的豪特曼星表包括了这两颗星,但豪特曼星表比凯泽的数据多出了数十颗恒星,参考豪特曼星表却只补充两颗不太亮的星似乎没有必要。

4 源流图

Elly Dekker曾对普朗修斯、洪第乌斯与布劳等人的天球仪进行比对,发现鲁道夫星表中的南天星表同时拥有凯泽与豪特曼的观测两个初始来源[7],我们将考察巴耶尔星图、豪特曼星表与鲁道夫星表之间的关系。由于巴耶尔星图与豪特曼星表均发表于1603年,因此它们之间可能是独立的,且豪特曼星表是附在一本小词典之后,在当时并不出名[6],巴耶尔星图参考了豪特曼星表的可能性不大。

我们将巴耶尔星图、豪特曼星表与鲁道夫星表在航海十二星座中的星数与相互之间的角距离偏差统计如下(表4):

表4 巴耶尔星图、豪特曼星表与鲁道夫星表中的星数比对与角距离偏差①(12)由于对部分不在十二星座图像中的游离恒星的统计口径不同,部分星座的星数可能略有差异,如鲁道夫星表中将夹白也列入了剑鱼座。θ1列为星座内同一颗恒星在巴耶尔星图与鲁道夫星表中坐标的角距离偏差的平均值,θ2列为星座内同一颗恒星在豪特曼星表与鲁道夫星表中坐标的角距离偏差的平均值,单位为度。

从表格中可以看出,鲁道夫星表中水蛇座与孔雀座中恒星的数量明显多于巴耶尔星图与豪特曼星表,这可能是因为同时采用了这两个来源。对于天燕座、天鹤座、印第安座、苍蝇座、孔雀座、南三角座等星座,θ2明显小于θ1,这表明鲁道夫星表中这些星座中的恒星的数据可能主要源于豪特曼的观测数据,开普勒在这部分星表的前言中却没有提到豪特曼的名字,这可能是因为开普勒也不知道自己实际上间接参考了豪特曼星表。对于剑鱼座、飞鱼座等星座,θ1明显小于θ2,这表明鲁道夫星表中这些星座恒星的数据可能主要源于凯泽的观测数据。

基于上述讨论,我们绘制出一幅《崇祯历书》南极增星部分来源间的关系图(图8):

图8 南极增星部分早期来源间的关系图①

5 结论

本文在前人研究的基础上,运用模拟绘图叠加、尾数分布统计与精度分析等方法,得出《崇祯历书》中星图与星表数据存在高度一致性的结论,且黄道坐标数据与赤道坐标数据间存在转换关系。在对《崇祯历书》星表中的恒星进行重新证认和分析后,我们为《崇祯历书》中南极附近增星数据来源提供了一个可能的解释,即《崇祯历书》星图和星表中的南极增星的直接来源应当为格林伯格星表与巴耶尔星图,最初的源头则是喜帕恰斯与凯泽的观测数据。《崇祯历书》与鲁道夫星表中的数据有一定的相关性,但不一致,这是因为它们有两个共同的源头——托勒密星表与巴耶尔星图,而鲁道夫星表又多出豪特曼星表这样一个间接来源。最终,我们绘制出一幅《崇祯历书》南极附近部分增星的源流图。