导数解答题中数列不等式的证明思路策略
2023-10-26 08:30张国飞
数理化解题研究 2023年30期
张国飞
(安徽省桐城中学,安徽 桐城 231400)
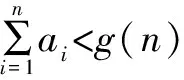
1 抓住常用思路,进行逐项比较





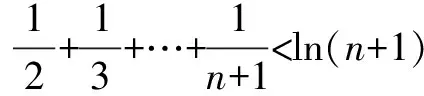
2 融合可选思路,利用数列单调(性)
例2设函数f(x)=(x-1)2+blnx,其中b为常数.
(1)判断函数f(x)在定义域上的单调性;

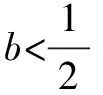
①当b≤0时,x1≤0舍去,而x2≥1,此时f′(x),f(x)随x在定义域上的变化情况如下表:

表1 函数单调性与导数关系






点评这里利用数列的单调性来证明相关的数列不等式成立时,其证明过程与逐项比较写的过程有点差异,但本质上两种方法之间有着异曲同工之妙.注意证明数列的单调性时,往往要回归题目前面部分所涉及的函数不等式问题,合理应用.
3 借助性质思路,合理放缩处理
例3已知函数f(x)=x-mlnx-1(m∈R)在x=1处取得极值A.
(1)求出实数m的值,并判断A是函数f(x)的最大值还是最小值;
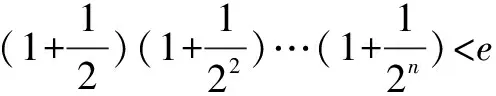


点评在解决导数解答题中数列不等式的证明问题时,往往要先从前面小题的过程或结论中选取合适的函数不等式加以应用,这非常考验考生的观察能力.而在对数列不等式进行累加求和处理后,合理的放缩是正确证明的关键,要注意观察所要证明的数列不等式的结构特征加以巧妙放缩处理.
在解决导数解答题中数列不等式的证明时,除了以上三种基本的证明思路策略,还可以借助推理与证明思维进一步加以综合与应用,利用可行的思路方法与技巧策略来剖析,有时在证明数列不等式时还可以多种证明思路策略联合应用,实现问题的综合应用与巧妙解决[4].
猜你喜欢
天中学刊(2022年4期)2022-11-08
语数外学习·高中版上旬(2022年2期)2022-04-09
新世纪智能(数学备考)(2021年11期)2021-03-08
新世纪智能(数学备考)(2020年11期)2021-01-04
黄河之声(2020年10期)2020-12-07
数理化解题研究(2020年19期)2020-07-22
中学生数理化·高一版(2019年9期)2019-10-12
读写算(2019年5期)2019-09-01
东坡赤壁诗词(2019年1期)2019-04-30
中学课程辅导·教学研究(2017年29期)2018-02-26

