活性材料冲击压缩及反应行为模拟方法研究进展

熊玮，张先锋，李逸，谈梦婷，刘闯，侯先苇

（南京理工大学 机械工程学院，江苏，南京 210094）

活性材料包括含能结构材料、含能非晶合金、含能高熵合金等金属基(或含金属聚合物基)复合材料或金属合金材料，是一种同时具备结构强度特性和化学反应释能特性的含能材料.该类材料在一般情况下保持惰性且不相互反应，但当给予足够的机械、电或激光等刺激后会迅速释放大量的化学能[1].由于兼具含能和强度两种特性，活性材料通常以活性毁伤元或活性防护结构的形式出现，如战斗部壳体[2-4]、高速破片[5-6]及聚能药型罩[7-10]、空间碎片防护结构[10-12]等.

在冲击压缩或强动载作用下，活性材料中将发生塑性变形、微射流、破碎及微孔塌陷等过程，因此冲击波阵面后将发生材料颗粒的迅速混合，最终引起温度的升高及材料内各组分的融合而发生化学反应[13-14].THADHANI 等[15]认为冲击波对活性材料内化学反应的激发与活性材料组分的变形及破碎密切相关.由冲击波激发的化学反应可分为两类[16-18]：一种是冲击辅助化学反应(shock-assisted chemical reaction，SACR)，另一种为冲击诱发化学反应(shock-induced chemical reaction，SICR).其中，SACR 发生在冲击脉冲卸载后，引发时间大于10 μs，遵循温度平衡原理，属于热-化学反应；而SICR 发生于冲击压力卸载前，引发时间尺度小于1 μs，遵循力学平衡原理，属于力-化学反应.活性材料在冲击作用下将发生如下三阶段响应过程：①活性材料由于受到剧烈的压缩作用产生冲击变形，形成瞬态超压和高温；②在冲击载荷达到一定阈值条件时，活性材料的化学反应被激发，并在持续的冲击作用下发展；③活性材料反应过程中内能增加，引起化学反应产物剧烈膨胀.在此过程中，由于活性材料的非自持反应特性，化学反应将在未受到冲击区域迅速衰减.相关研究表明，随着冲击加载强度的提高，活性材料由部分化学反应转变为完全化学反应，进一步提高释放的化学能[14,19].阐明活性材料在典型加载条件下的冲击反应机制，同时结合基于理论和数值仿真方法建立活性材料的冲击反应预测模型是活性材料研究的基础.

国内外针对该类材料冲击压缩动力学响应特性已开展了大量的理论研究工作，能够对该类多组分复合材料的冲击加载压力和温度关系进行较好的预测[20-22].在活性材料冲击反应行为的热化学模型方面，BOSLOUGH[14]建立了考虑冲击反应温升贡献的理论模型，并通过与试验结果对比提出材料在冲击加载过程中仅发生了部分化学反应的观点.目前，学者普遍认为冲击反应主要由温度控制[23-25]，相关学者将经典的化学反应动力学方程与冲击温升结果相关联[23]，从而建立模型描述该类材料在不同冲击加载条件下的冲击反应效率，并结合试验确定了冲击反应热化学模型相关参数[26-27].

由于活性材料的冲击释能特性较难通过商业有限元软件中已有的材料模型进行描述，前期相关研究工作主要集中于活性材料力学响应和冲击反应行为试验及含能毁伤元对典型目标毁伤效果的试验验证上[6,28-29].近几年，为了完善活性材料冲击反应机制的研究，推进该类材料的设计与应用，考虑活性材料冲击反应行为的数值模拟方法得到了快速发展.活性材料通常包括两种或两种以上的组分，其宏观力学性能及冲击反应特性受控于细观结构.因此，研究人员在不同的时空尺度开展了活性材料的冲击压缩及反应行为的数值模拟方法研究工作，为阐明该类材料的冲击反应机制、实现工程化应用奠定了基础.

本文主要针对活性材料在不同尺度的冲击动力学响应和化学反应行为数值模拟方法的研究进行梳理，总结典型活性材料的细观结构特性和针对不同细观结构特性的分子动力学模拟进展，回顾活性材料冲击压缩特性细观模拟方法，重点介绍基于不同扩散速率假设的活性材料冲击反应特性跨尺度模拟方法，归纳与总结活性材料冲击反应行为宏观尺度数值模拟方法，并对后续研究进行展望.

1 活性材料细观结构特性

活性材料中最为典型的是含能结构材料，自21世纪初起受到了大量的关注，通常为金属间复合材料(如Al/Ni、W/Zr 等)或金属及高分子化合物复合材料(如Al/PTFE、Ti/PTFE 等)，其细观结构特性受控于制备工艺.活性材料的制备方法包括准静态压制[30-31]、爆炸烧结[32]、铸造[33]、冷轧[34-35]和物理气相沉积[36]等，通过采用不同的制备方法和制备工艺可获得具有不同细观结构特性的活性材料，从而实现该类材料力学和化学性能的调控.根据活性材料原材料形态，可将其划分为颗粒复合材料和叠层复合材料两种.

1.1 颗粒复合活性材料细观结构

颗粒复合活性材料的原材料为微米/纳米尺寸的不同颗粒形状(球形、片状、不规则形状等)的粉末，将其按照一定的配比混合均匀后采用准静态压制、爆炸固结或铸造等工艺进行制备，三种典型的制备方法如图1 所示.其中，准静态压制是最常见的一种含能结构材料制备方法，具有制备成本低、工艺简单的优点，但受到压机压力条件的限制，由该方法制备得到的活性材料通常具有一定的孔隙率.爆炸固结法通过爆炸冲击波的高压作用将活性材料粉末进行压实，可获得完全密实的活性材料，但同时由于剧烈的高温高压作用而导致其制备的活性材料界面易产生金属间化合物.铸造法主要适用于聚合物(如环氧树脂等)基活性材料，通过将金属粉末与融化后的聚合物混合在一起并注入模具中固化成型.

图1 三种典型颗粒复合材料的制备方法Fig.1 Three typical preparation methods for reactive powder composites

由于初始粉末经过了充分的混合，颗粒复合活性材料的细观颗粒分布较为均匀.图2 所示为WEI等[32]采用爆炸烧结法制备的等摩尔比的金属(Nb、Ni、Mo、W 或Ta)/Al 颗粒复合材料扫描电子显微镜(scanning electron microscope, SEM)照片，通过观测发现W/Al 和Ni/Al 两种材料形成了以Al 为基体的细观结构，而其余三种材料分别形成了以Mo, Nb 或Ta 为基体的细观结构，而造成以上两种截然不同细观结构的根本原因在于粉末初始形状、尺寸的区别.进一步，结合静/动态力学性能测试和细观观测手段，WEI 等[32]得出了材料中的基体成份控制其抗压强度的结论.此外，XIONG 等[31]、EAKINS 等[19]采用球形Al 粉与树枝状或片状的Ni 粉进行混合，制备了与WEI 等[32]具有不同细观结构的Ni/Al 颗粒复合材料，如图3 所示.其中，XIONG 等[31]获得了以Ni 为基体的Ni/Al 颗粒复合材料细观结构，该材料准静态压缩破坏特性与WEI 等[32]也有显著区别；而EAKINS 等[19,38-39]通过细观模拟方法和飞片撞击试验证实了Ni/Al 颗粒复合材料的冲击压缩特性与初始材料颗粒形状及密实度有关.因此，颗粒复合材料的力/化学特性通常与其原始粉末的类型、形状、颗粒大小及所压制试件的密实度等关联.

图2 金属/Al 的扫描电镜照片[32]Fig.2 Cross-sectional SEM micrographs of consolidated mixtures[32]

图3 两种典型Ni/Al 颗粒复合材料SEM 照片Fig.3 Cross-sectional SEM micrographs of Ni/Al

1.2 叠层复合活性材料细观结构

叠层复合活性材料主要由物理气相沉积和冷轧方法制备而成，其制备过程示意图如图4 所示.其中，物理气相沉积法是一种真空镀膜的方法，在真空条件下将气化为原子尺度的原材料逐层沉积在基体表面，能精确控制叠层复合材料的材料层厚度，但存在加工成本高、耗时长等缺点[36].冷轧技术指在一定压力下将相互间隔的原材料板材进行反复轧制而结合在一起的过程[40]，通过轧制次数控制材料层厚度.

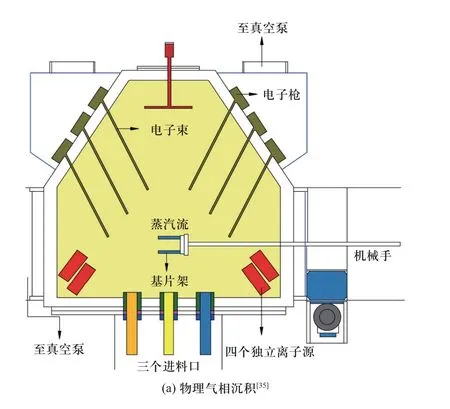
图4 两种典型叠层复合材料制备方法示意图Fig.4 Two typical preparation methods for multi-layered reactive composites

两种加工工艺形成的典型活性材料细观照片如图5 所示.其中，通过物理气相沉积法获得的多层细观结构相对均匀(图5(a)).由冷轧技术制备的活性材料细观结构的不均匀性较为明显(图5(b))，且界面间通常会出现一定的金属间化合物(图6)，对该类材料高温自蔓延合成(self-propagating high-temperature synthesis, SHS)过程的反应速度有一定的影响[11].叠层复合的活性材料冲击压缩特性除了与材料层的厚度相关外，还与材料载荷方向相关[36,41-42].

图5 两种典型Ni/Al 叠层复合材料SEM 照片[36]Fig.5 SEM images of Al/Ni multilayer composites[36]

2 活性材料冲击压缩及反应行为分子动力学模拟进展

动态载荷下活性材料的力学响应与化学反应释能行为，其本质在于原子运动改变了其排布方式与化学键重组.基于求解原子运动方程的分子动力学(molecular dynamics, MD)模拟方法，可以得到整个系统内粒子位置和速度的动态演变过程.在冲击压缩条件下，活性材料体系内部应力、温度和粒子速度分布不均衡，使得化学反应的激活愈加复杂.借助于分子动力学方法，可揭示活性材料冲击诱发化学反应机制，分析不同微观特征(原子比、晶向、尺寸、相态、形貌、排布等)活性材料的冲击反应行为.根据细观结构特性，可将分子动力学模拟研究工作分为颗粒复合材料和叠层复合材料的分子动力学模拟两个方面.

2.1 颗粒复合活性材料冲击压缩及反应行为分子动力学模拟进展

对于Al/Ni 颗粒复合材料，CHERUKARA 等[44-45]研究了疏松态Al/Ni 材料准二维颗粒系统在冲击加载下的热力学响应以及后续化学反应行为，揭示了不同速度范围梯度下的活性材料冲击反应特性(图7)：低速(＜0.75 km/s)冲击下，微孔塌陷引起活性材料的快速反应，但反应速度随后显著减慢；中速(≈1.00 km/s)冲击下，原位热动能足以支撑自持放热反应，化学反应时间在纳秒尺度；高速(≥1.50 km/s)冲击下，原位热动能与孔隙坍缩释放的热能驱动了快速化学反应.XIONG 等[46-48]先后探究了Al/Ni 纳米颗粒混合物和接近完全致密的Al/Ni 的晶粒混合物的冲击响应与冲击诱导化学反应，研究结果表明颗粒配位数和体系密度对颗粒材料的形变和反应有显著影响.在多晶结构中塑性形变主要出现在晶粒界面或晶粒间结点处，易于形成热点.在高强度冲击下，Al 优先熔化加速原子间的混合和反应，可能形成局部微型涡旋.

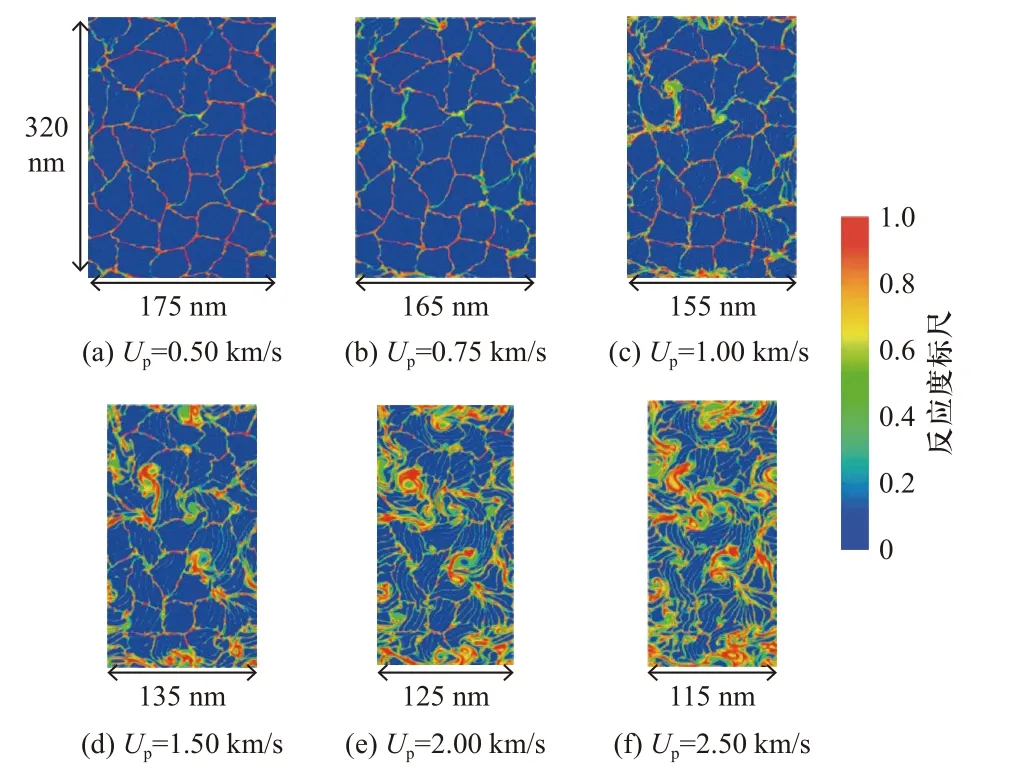
图7 不同冲击压缩速度下冲击加载结束时的反应度[45]Fig.7 Extent of reaction at the end of the shock loading process for different piston velocitie[45]

为了研究球磨试样冲击诱发化学反应机制，MANUKYAN 等[49]建立了Al/Ni 纳米复合结构低速冲击下放热反应行为计算的分子动力学模型.通过将模型中圆柱形颗粒设置为空心结构来模拟实际试样中的孔隙，获得了冲击加载下活性材料微观尺度上热点和反应坐标分布情况，如图8 所示.结果表明，即使没有发生孔隙坍塌，在发生局部塑性变形和机械混合的区域也产生显著的局部高温，且沿着孔隙表面和Ni/Al 界面处发生了较大程度的材料混合.

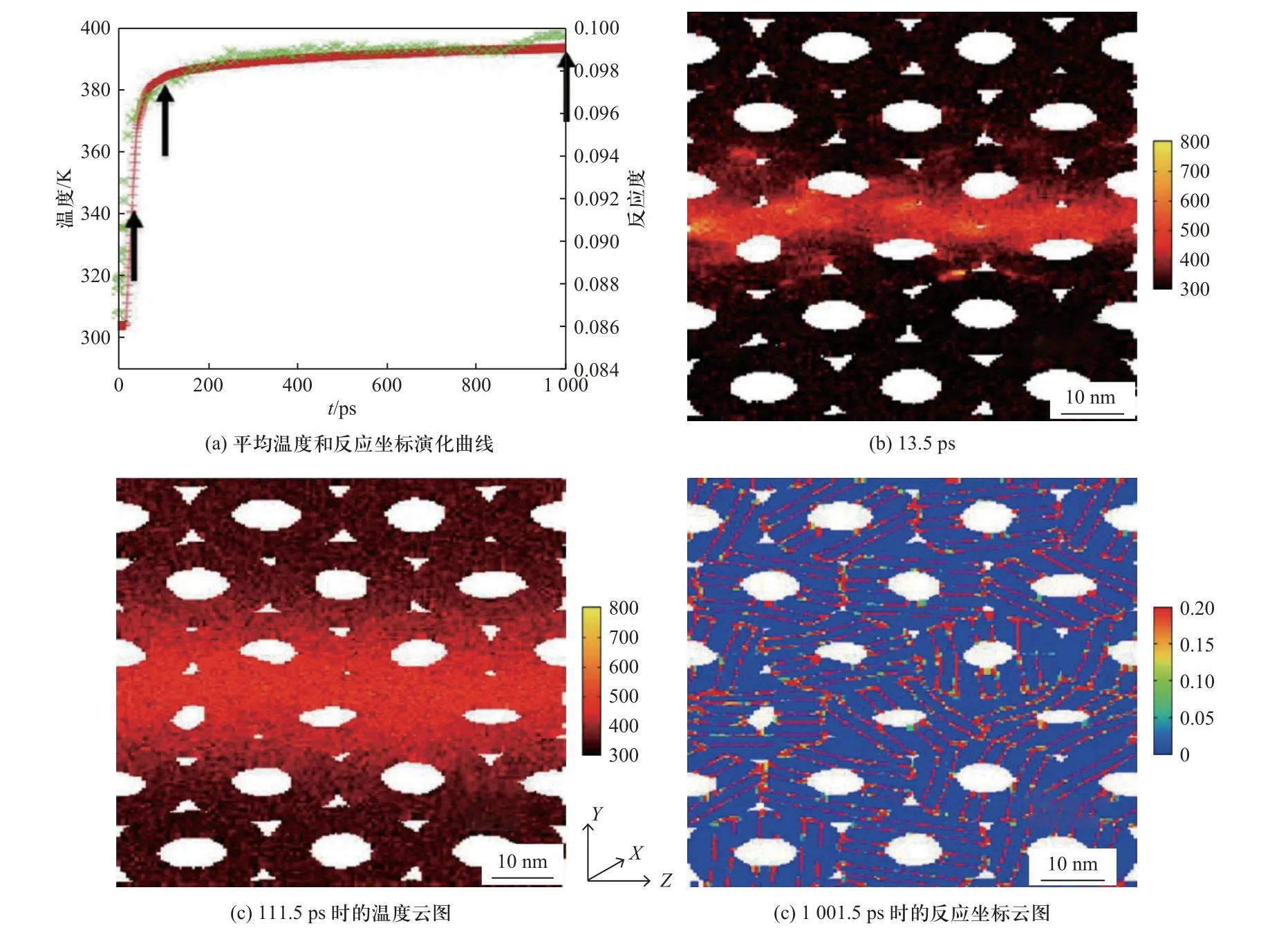
图8 含孔隙Al/Ni 在250 m/s 冲击压缩条件下的分子动力学模拟计算结果[49]Fig.8 MD simulation results of porous Al/Ni samples at shock loading of 250 m/s[49]

2.2 叠层复合活性材料冲击压缩及反应行为分子动力学模拟进展

对于叠层复合活性材料，ZHAO 等[50-52]发展了结合对称冲击方法和收缩周期性边界方法，先后探究了理想Al/Ni 纳米叠层结构和含孔洞结构的冲击反应过程(图9)，研究结果表明，2 km/s 和3 km/s 的冲击速度均能诱发化学反应，孔洞坍缩与原子喷射导致更高的局域温度，加速了原子的扩散与混合，体系内温度高于理想Al/Ni 纳米多层结构.TIAN 等[53]探究了不同冲击强度下Al/Ni 纳米叠层结构的层裂，并指出当冲击速度较高时，化学反应的激活形成Ni-Al 金属间化合物从而提高层裂强度.由于存在自由面卸载，在该研究中化学反应无法持续.

同时，学者们针对具有非平行界面的叠层复合材料也开展了相关研究工作.TERRETT 等[54]的研究结果表明，在相同撞击条件下，碰撞界面处的材料和形貌差异并不会导致长时间下体系整体热力学状态的产生显著差别.谢轶凡等[55]针对具有正弦界面特征的Al/Ni 材料开展分子动力学模拟，探究了非对称碰撞下冲击波从“软”物质入射“硬”物质和“硬”物质入射“软”物质时，界面的Richtmyer-Meshkov(RM)不稳定性增长、原子扩散和化学反应，结果表明界面不稳定性影响了反应的传播机制，典型计算结果如图10 所示.

3 活性材料冲击压缩特性细观模拟方法

分子动力学是基于材料晶体结构建模的确定性模拟方法，在研究材料动力学响应的微观机制方面具有独特优势，尤其在高温高压极端加载条件下更加显示其不可替代的作用.但同时，分子动力学模拟受限于极小颗粒尺度(数十至数百纳米级)和极短时间尺度(纳秒)的计算条件[50]，活性材料在更大时间、空间尺度下冲击压缩变形、破碎及混合等过程需要借助细观尺度模拟手段进行预测分析.目前，活性材料细观模型的生成方法主要有基于分布统计规律的细观模型建立方法和基于SEM 照片的细观建模方法两种.

3.1 满足分布统计规律的细观数值仿真模型

在活性材料冲击响应特性细观模拟中，最常用的手段是结合材料中颗粒细观分布特性(材料配比、尺寸、几何形态)建立相应的数学描述，并利用随机数生成方法、模拟退火算法等方法生成满足细观分布统计规律的模型[57-63].在建模过程中，通常基于活性材料的细观结构特性将其中一种材料组分设置为基体，而其余材料按照其颗粒初始形态进行随机投放，投放过程中需保证颗粒间互不重叠.

以双组分活性材料(Al/Ni、Al/PTFE 等)为例，将其中一种组分A视为基体材料，而另一种组分B均匀分布其中.假设B为等粒径(R)的圆形颗粒，将其颗粒位置(xi，yi)按照随机分布方法进行分配，通过控制颗粒的间距保证其不相互重叠[61,64]

式中：XL和YL为仿真模型的尺寸；i，j为颗粒序号；ui，vi分别为(0,1)和(-1,1)之间的随机数.

通过控制B颗粒的投放数量N，可以严格控制其体积分数[64]

典型的满足分布统计规律的活性材料细观模型及其在典型冲击加载条件下的颗粒变形、压力分布及冲击波速度Us-粒子速度Up曲线如图11 所示.基于该种细观建模方法，可对颗粒尺寸、形状、配比等典型的细观因素进行系统性的研究.近几年，SMITH等[65-66]针对高密实度Al/Ni 类活性材料建立了两种组分均随机分布的细观模型.在该细观模型中，Al、Ni 颗粒为椭圆或圆形，最终建立的模型密实度可达96%.除了材料压缩过程中的塑性变形、颗粒碰撞等过程外，SMITH 等[65-66]还考虑了颗粒间摩擦力的影响，对Al/Ni 材料中的颗粒变形、压力分布和热点形成过程进行了更精细的计算(图12).

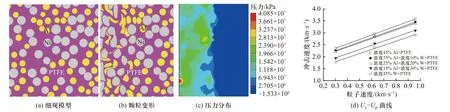
图11 基于材料颗粒分布特性生成的细观模型及其在典型冲击加载条件下的颗粒变形、压力分布及Us-Up 曲线[61]Fig.11 Random granules distribution numerical mode, the deformation morphology, pressure distribution during shock compression and Us-Up relationships l[61]

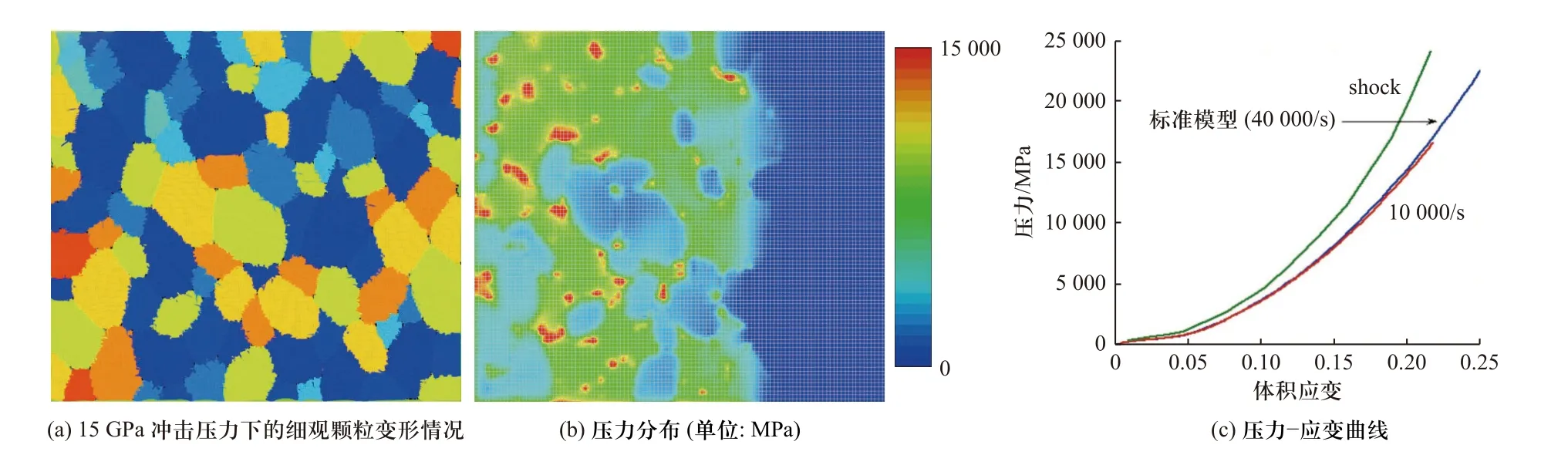
图12 密实度为96%的Al/Ni 材料的细观模拟结果[65]Fig.12 Mesoscale simulation of Al/Ni with 96% of theoretical material density (TMD)[65]

3.2 基于细观照片生成细观尺度数值仿真模型

虽然满足分布统计规律的细观尺度数值仿真模型的建立较为方便快捷，但该方法在体现材料细观尺度上的实际分布特点方面仍存在一定的误差，尤其不适用于各组分材料细观颗粒形状不规则或大量团聚的情况[64].针对该问题，基于细观照片生成细观尺度数值仿真模型的方法更加适用.图13(a)为分别采用球状和片状Ni 颗粒与球状Al 颗粒混合制备的Al/Ni 材料SEM 照片和相应的细观尺度数值仿真模型[39].该模型的建立过程主要有三步[38]：区分相、矢量化、导入仿真软件.首先，基于不同材料在细观照片(SEM 或光学显微镜照片)上呈现的颜色和形态差异，对活性材料各组分占据的位置进行区分.然后，将细观照片矢量化，使之成为能够通过具体数学方法描述的点、线及多线段.其中，细观照片的放大倍数和所选区域必须能反映材料颗粒的分布规律和配比，从而保证由此得到代表性体积单元(representative volume element，RVE)的有效性.通常，SEM 拍摄的区域有限，RVE 的尺寸过小而不足以模拟整个冲击压缩过程中的材料细观尺度上的变形行为及冲击波传播规律，因此需要采用镜像或者复制扩展的方法获取尺寸更大的细观模型.

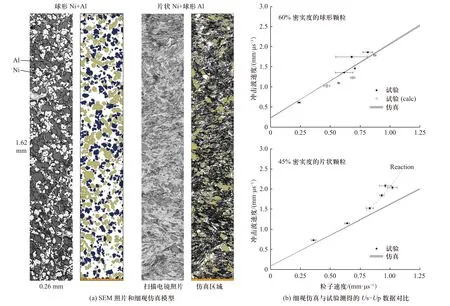
图13 两种典型Al/Ni 材料的细观模型和计算结果[39]Fig.13 The mesoscale model and simulation results for two typical Al/Ni composites[39]

通过该建模方法，EAKINS 等[38-39]研究了材料颗粒形状和密实度等细观特性对Al/Ni 颗粒复合材料冲击响应行为的影响规律.图13(b)为两种典型颗粒形状的Al/Ni 材料细观模拟Us-Up关系与试验结果对比情况.可以发现，在低速冲击条件下，细观模拟结果与试验结果吻合较好；而在更高的速度冲击下，Al/Ni 材料发生了化学反应，试验测得的冲击波速度高于细观模拟结果.另一方面，由于叠层复合的活性材料细观结构不均匀，且颗粒分布具有一定的方向性，基于细观照片生成的细观模型方法对其更加适用，在相关研究中需要同时细观层厚度、冲击加载方向和颗粒间复合物的影响[41-42].随着细观观测手段的发展，微计算机断层扫描等技术手段可获得活性材料的三维细观结构，为活性材料三维细观模型的建立提供了新的技术途径[67-68].

4 活性材料冲击反应特性跨尺度模拟方法

活性材料的细观结构特性对材料的冲击压缩和反应行为均有显著的影响.采用多尺度方法研究活性材料的冲击反应行为本质是建立微观-细观-宏观不同尺度下材料冲击动力学及化学耦合过程的关联机制，为准确预测该类材料在冲击载荷下的力学行为和化学反应特性提供技术途径.关于活性材料冲击反应多尺度方法研究的公开报道较少，究其原因主要有以下几点[69]：

①细观尺度上建立考虑冲击引起化学反应的模型难度较大；

②将化学反应与材料的力学性能结合的过程比较复杂；

③缺乏描述非均匀化学反应的宏观连续化学反应模型.

4.1 活性材料反应扩散模型

对于目前研究比较热门的Al/Ni、Al/PTFE 类活性材料，化学反应主要发生于材料内各组分之间.因此，在该反应类型的活性材料冲击反应机制研究方面，主要采用细观尺度建模的方法，而大多数冲击反应细观模型均建立在考虑物质扩散过程的基础上.随着活性材料化学反应的进行，两种材料的反应产物影响了反应物间的相互接触，反应物需穿过产物层才能与另一边的反应物继续反应，从而会抑制反应的进一步发展.通常采用Fick 第二定律描述该非稳态扩散过程[70]

式中：x、y、z为空间坐标系坐标值；D为扩散系数；C为浓度

式中D0和Ed分别为扩散系数的指前因子和扩散活化能.

随着扩散过程的进行，活性材料内的化学反应得以维持，即活性材料在冲击条件下发生了反应扩散过程，其中扩散是控制因素[70].在此过程中，材料系统始终遵守质量守恒定律，即物质浓度的变化率等于浓度梯度引起的浓度变化率与化学反应引起的浓度变化率之和[70]，由此推导得到材料的反应扩散方程

式中： γK j为组元K参与第j个化学反应的分子量所占的总反应分子量的比例常数；Rj为第j个化学反应的反应速度，从第1个到第r个化学反应引起的K组元总的浓度变化率为.

4.2 基于物质扩散速率无限大假设的活性材料冲击反应行为计算模型

由于缺乏关于冲击加载条件下物质扩散系数的试验数据，部分学者提出了物质扩散速率无限大、且化学反应程度与物质运输过程无关的假设.以DO等[71-72]为代表的学者在BENSON[57,73]提出的基于欧拉算法的动力学仿真代码的基础上加入了化学反应动力学方程，对空间非均匀化学反应过程进行了计算分析.基于相同的假设，乔良等[60-61,74]利用ANSYS/AUTODYN 非线性有限元分析软件在不考虑冲击反应情况下实现了活性材料冲击压缩过程的细观模拟.然后，建立细观冲击响应与宏观反应行为的关联机制，以细观模拟动力学响应结果为输入量，引入冲击反应动力学方程得到了宏观尺度冲击反应计算结果，计算流程如图14 所示.物质扩散速率无限大的假设适用于冲击反应在冲击波传播后极短的时间尺度内完成的情况，但未考虑时间尺度上冲击反应的发展过程和冲击反应对冲击波的影响机制，对颗粒尺度较大的活性材料冲击反应行为的描述存在较大的误差[72].

4.3 基于扩散速率为定值假设的活性材料冲击反应行为计算模型

另一部分学者认为，物质扩散速率是有限的，且为与材料内的压力、温度和应变率等无关的定值.其中，LOMOV 等[75]将冲击加载下的材料扩散速率取为与常规加热试验获得的参数一致，针对纳米级颗粒尺度的活性材料冲击反应行为开展计算，发现其能在百纳秒级时间内完成化学反应，与相关试验结果吻合[75]，相关计算模型和结果如图15(a)所示.基于该假设条件对微米级尺度(2～3 μm)的Al/Ni粉末混合物的冲击反应行为开展细观模拟，能够得到材料细观尺度颗粒变形、物质扩散及进一步的化学反应过程.但从反应产物(图15(b)计算结果的深色部分)分布情况可以看出，基于常规扩散速率的计算模型得到的冲击压缩条件(0.5～0.9 km/s)下的材料反应度不高，反应产物的质量分数仅为1%～12%[75].

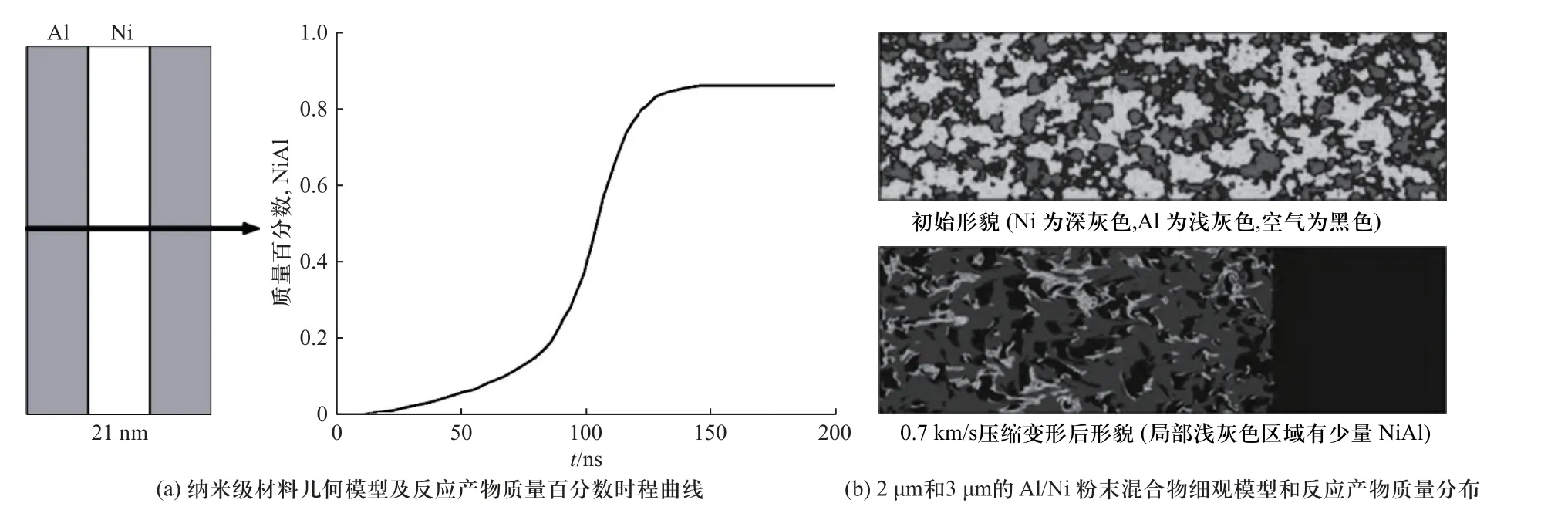
图15 常规扩散速率数值模拟[75]Fig.15 Simulation with regular transport rates[75]

因此，目前大部分学者开始认为冲击反应中的物质扩散速率远大于常规由物质浓度控制的扩散速率.其中，SIVA 等[76]针对冲击条件下的物质高度扩散过程提出了一种“伪扩散”模型，将反应扩散模型(7)的一维模式中的相关参数进行了如下量纲一化处理

式中：下标A、B分别对应材料组分；t0为发生完全化学反应需要的时间；x0为时间t0内物质扩散影响的范围.

SIVA 等[76]针对铌(Nb)/硅(Si)粉末混合物中为一维扩散反应过程进行计算，得到Si 的量纲一化浓度在量纲一化时间t/t0内随着量纲一化距离x/x0变化的曲线如图16(a)所示.基于该“伪扩散”模型，可以推测细观颗粒尺寸为30～50 μm 的材料在800 K 的温度下完成冲击反应过程所需要的扩散速率应为10～35 m2/s.由此进一步确认，冲击加载条件下，活性材料内发生了极高程度的物质扩散过程.SIVA等[76]基于该模型，采用光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)算法对铌(Nb)/硅(Si)粉末混合物的反应扩散过程进行了计算，将物质扩散过程简化为化学反应速率随材料节点到材料界面距离的变化关系，结果如图16(b)所示.通过对化学反应释放的能量进行更新，可以对冲击反应温升行为进行较好的描述.此外，国内相关[37,77]针对Al/Ni类活性材料的冲击反应行为开展了跨尺度计算与讨论，同样得出冲击加载条件下的物质扩散速率远大于常规条件的结论.

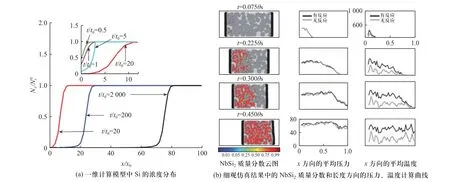
图16 基于“伪扩散”模型的计算结果[76]Fig.16 Calculation results based on “pseudo-diffusion” model[76]

4.4 基于扩散速率与温度/应力状态相关假设的活性材料冲击反应行为计算模型

通过前述总结可知，仅基于物质浓度控制的扩散机制不足以描述活性材料在冲击加载下的反应行为.因此，REDING 等[13,69,78-79]将物质扩散速率与温度和应力状态联系起来，将式(6)修正为

在此假设条件下，REDING 等[13,69,78-79]开展了典型活性材料在颗粒尺度(granular level reaction，GLR)的冲击反应特性计算，同时建立了非均质材料的细观尺度化学反应(mesoscale reaction，MSR)模型.进一步，由MSR 模型计算结果(图17(a))中物质的质量分数确定材料宏观反应速率，由此实现了活性材料冲击反应行为的跨尺度计算.通过对Fe2O3/Al 和Al/Ni两种体系的材料进行跨尺度计算，并将最终得到的宏观尺度计算结果与试验对比(图17(b))，验证了所建立的多尺度模型的可靠性.

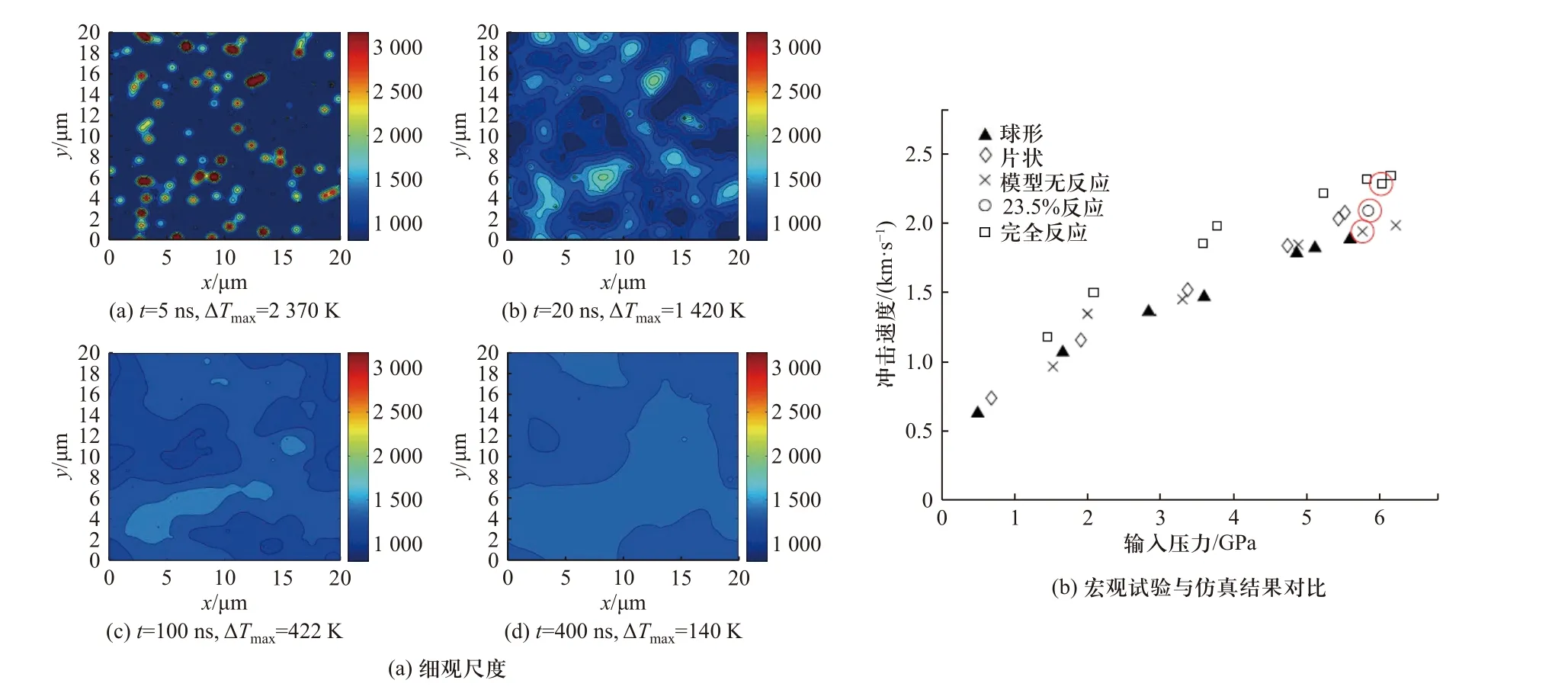
图17 考虑压力和温度对扩散速率影响的Al/Ni 材料冲击反应计算结果[13]Fig.17 The calculation results considering the pressure and temperature effects on the diffusion rate[13]

5 活性材料冲击反应行为宏观尺度模拟方法

基于前述分子动力学模拟、细观尺度及跨尺度模拟方法，可对考虑细观结构特性影响的活性材料冲击反应机制进行深入研究，有助于指导该类材料的设计与应用.为了在毁伤元或防护结构中充分利用活性材料的冲击反应释能特性、实现能量有效调控，考虑其冲击反应行为的数值模拟方法是进行毁伤元结构设计及毁伤效能预测必不可少的重要手段.在此过程中，难点在于活性材料本构模型的选取与构建.

5.1 活性材料冲击动力学本构模型

活性材料的冲击动力学本构模型主要用于描述未反应材料力学响应特性，主要包括强度模型和冲击状态方程.在强度模型方面，对于Al/PTFE、Al/Ni等典型含能结构材料，通常采用Johnson-Cook (J-C)模型描述材料的塑性变形和失效行为[11,80-83].表1 为两种典型活性材料的Johnson-Cook 模型主要参数.其中，A、B、C、n、m为材料常数，D1～D5为材料损伤参数.对于同一种活性材料，由于制备工艺或配方的差异，学者采用的本构模型参数存在差异[81-82].

表1 典型活性材料的Johnson-Cook 模型主要参数Tab.1 Main parameters for the Johnson Cook model of typical reactive materials

此外，对于近几年受到广泛关注的非晶合金材料，由于几乎没有塑性变形阶段，主要采用Johnson-Holmquist II (JH-2)模型描述其脆性特性[86-88].目前，学者们针对锆基非晶合金材料开展了大量的研究工作，三种典型锆基非晶合金JH-2 模型主要参数为见表2.其中，A'、B'、C'、N、M为材料常数，σHEL为材料的Hugoniot 弹性极限；pHEL为材料处于的Hugoniot 弹性极限时的压力分量.

表2 典型非晶合金JH-2 模型主要参数Tab.2 Main parameters for the JH-2 model of typical amorphous alloys

活性材料的冲击响应行为通常由Mie-Grüneisen 状态方程[89]描述.表3 为两种典型的活性材料冲击状态方程参数，其中C0为材料声速；S为材料常数.

表3 典型活性材料冲击状态方程参数Tab.3 Main parameters for the shok equation of state of typical reactive materials

5.2 基于点火判据的冲击反应行为分步计算数值模拟方法

由于活性材料的冲击释能特性较难通过商业有限元软件中已有的材料模型进行描述，前期相关数值模拟主要集中在其力学响应特性方面.结合其在极端加载条件下的力学响应和温度响应结果分析冲击反应行为成为了一种比较常规的手段.随着活性材料在高效毁伤与防护领域的发展，考虑冲击反应释能行为的数值模拟方法逐渐受到重视.

其中，基于活性材料的冲击动力学响应结果，结合点火判据进行“惰性+活性”分步计算是一种常用的仿真手段.在此方法中，应用较多的有弛豫时间(又称点火延迟时间)和点火阈值两种点火判据.

活性材料冲击反应存在弛豫时间[91-92]，MOCK等[93-94]通过泰勒杆撞击实验获得了活性材料反应弛豫时间与撞击压力的关系

式中：t为反应弛豫时间；σTS为发生点火需要的最小应力；a，b，c为与粒径有关的材料常数.

对于聚能装药战斗部中的活性材料药型罩，其射流成型时间小于冲击反应弛豫时间，可近似认为在活性射流成型过程中未发生化学反应；而射流侵彻靶体作用过程较长，活性材料可能发生化学反应，在此过程中考虑化学反应产物的膨胀过程是描述活性材料毁伤增强效应的关键.LI 等[95]在活性药型罩射流对有限厚钢靶毁伤效应研究中，首先采用冲击状态方程和J-C 模型计算了活性射流的成型和侵彻靶板过程；进一步在活性材料作用时间达到弛豫时间后，采用炸药的JWL 模型计算其类爆轰反应过程，分析了活性射流对钢靶穿孔增大的原因.典型活性材料JWL 模型参数见表4.

表4 典型活性材料JWL 模型参数Tab.4 Parameters for the JWL model of typical reactive materials

活性材料化学反应持续时间较长，燃烧速率较慢，产生的超压显著低于高爆炸药，部分学者认为传统的高爆炸药JWL 模型并不适用于活性材料[96]，而选用Powder-Burn 状态方程模拟活性材料的冲击反应行为.张雪朋等[90,96]假设活性材料在射流成型和侵彻阶段保持惰性，侵彻结束后发生爆炸反应，采用分步计算方法分析了活性射流对混凝土靶的毁伤效应.图18(a)、(b)为活性射流侵彻混凝土靶阶段典型损伤云图，图18(c)、(d)为活性射流在孔内发生类爆轰时对混凝土的损伤云图.

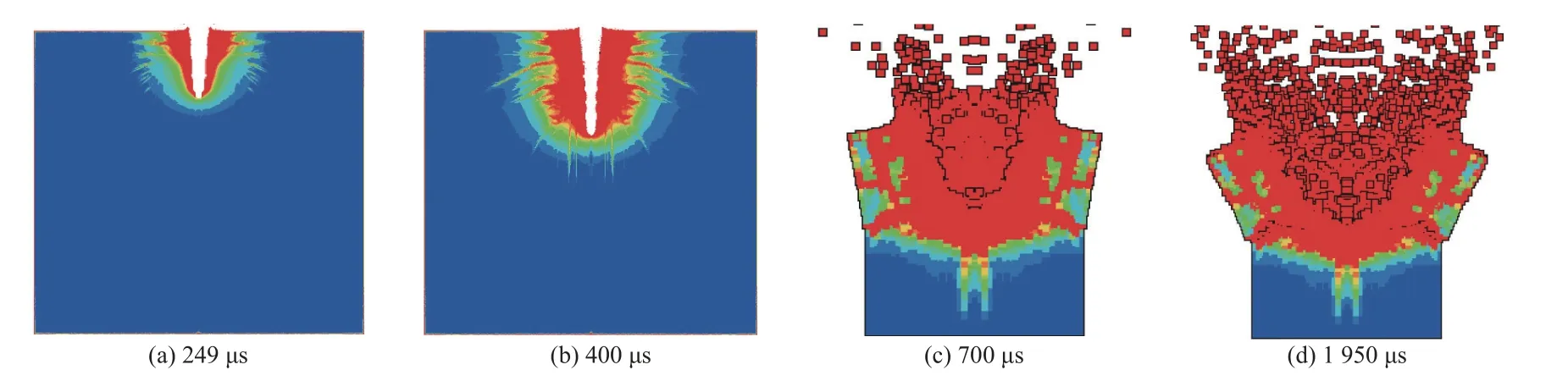
图18 活性射流对混凝土靶毁伤效应模拟[90]Fig.18 Damage effect of the reactive jetting on the concrete target[90]

另一方面，活性材料的冲击反应行为存在阈值条件[98]，根据活性毁伤元与目标作用过程中的压力分布可初步判断其是否化学反应.黎勤[97]、LI 等[99]以活性破片为研究对象，基于其侵彻多层靶过程中的压力分布结果和冲击反应阈值条件确定化学反应被激活的区域.通过重新建模，在反应激活区域使用Powder-Burn 模型开展数值模拟，分析了活性材料反应释能对多层靶的毁伤增强效应.图19 所示为活性破片侵彻双层靶数值仿真模型和典型仿真结果.

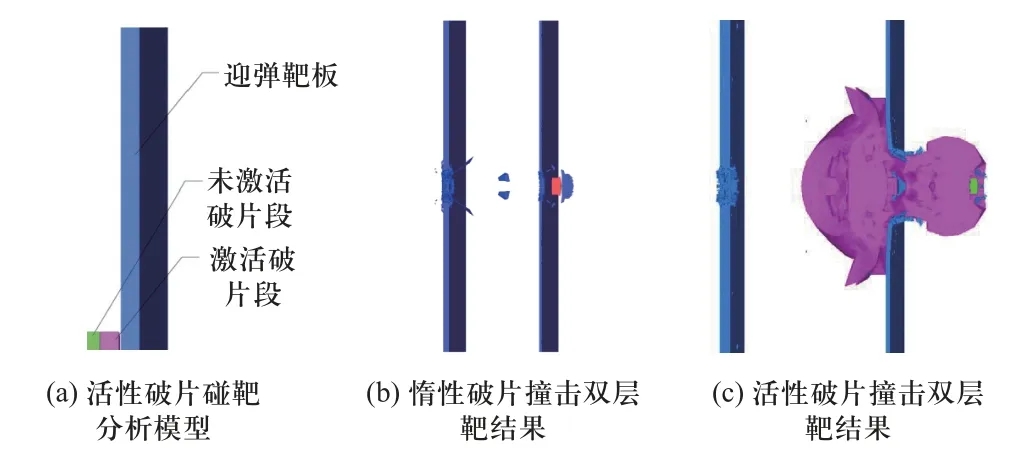
图19 活性破片侵彻双层靶过程模拟[97]Fig.19 The simulation of reactive fragments impact on double-spaced plates[97]

5.3 基于炸药点火增长模型的冲击反应行为数值模拟方法

在不同的冲击加载条件(压力、时间等)下，活性材料将呈现无反应、部分反应到完全反应三种程度的化学反应释能行为[26,100].为了全面考虑活性材料化学反应激发和发展过程，采用Lee-Tarver 三项式点火增长模型或其改进模型建模是目前使用较多的一种数值模拟方法[101].Lee-Tarver 模型中的三项式分别描述材料的热点形成、慢速反应和快速反应过程，由于活性材料的冲击反应速率较低，快速反应过程对冲击波压力影响较小，通常忽略三项式中的快速反应项[102-103].武强、任思远等[10-11,81-82]将活性材料应用于空间碎片防护结构中，基于改进的Lee-Tarver 模型对Al/PTFE 和Ti/PTFE 活性材料的冲击诱发化学反应行为进行描述，计算了破片超高速侵彻活性材料防护结构过程中碎片云形成过程、形貌特征及其对后效靶破坏特性，揭示了活性材料防护结构超高速撞击防护机理.两种活性材料的Lee-Tarver 模型参数和典型计算结果分别如表5 和图20 所示.

表5 典型活性材料Lee-Tarver 模型参数[11]Tab.5 Main parameters for the Lee-Tarver model of typical reactive materials[11]

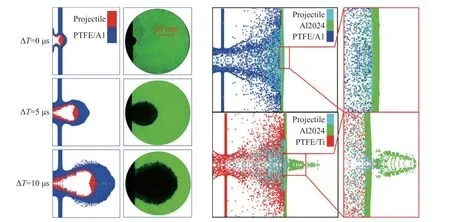
图20 破片超高速撞击活性材料空间防护结构数值模拟[10-11]Fig.20 The simulation of hypervelocity impact of the spherical projectile on reactive material bumper[10-11]

为了进一步考虑活性材料冲击点火弛豫时间和聚合物分解产生点火的问题，肖建光等[104-105]在AUTODYN 显示动力学有限元分析软件中进行二次开发，添加了活性材料的双点火准则[104-105]

式中Td为活性材料中聚合物的分解温度.基于该方法对活性材料弹丸高速侵彻双层间隔铝板冲击释能过程进行数值模拟，获得典型位置压力、温度和反应度随时间的变化曲线，并将反应度变化趋势与试验中活性材料弹丸释能发光过程进行对比.其中，Al/PTFE 活性侵彻体在550 m/s 的点火过程如图21所示.该方法可对冲击引起的活性材料力学响应和化学反应时间尺度耦合过程进行更精确的描述与预测.

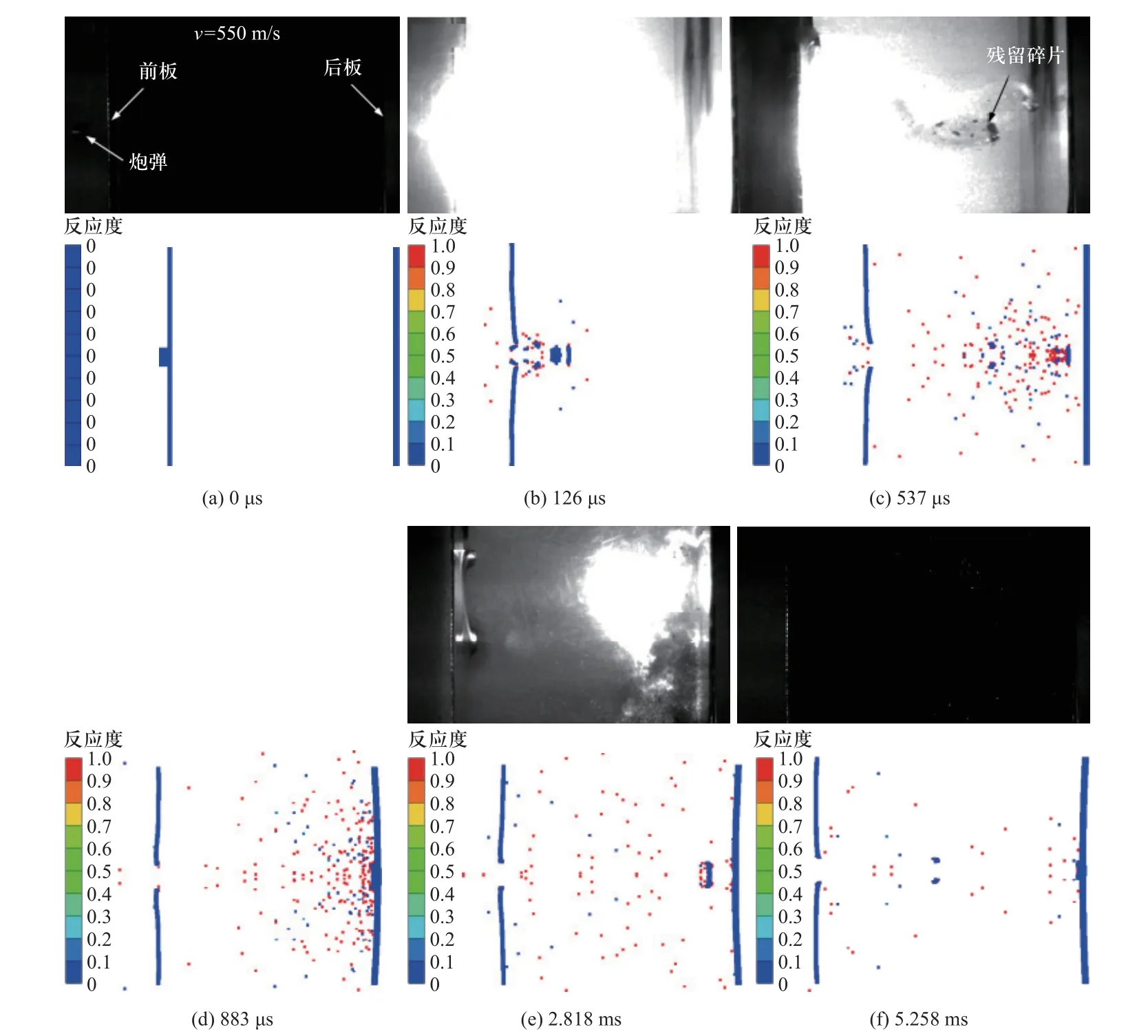
图21 Al/PTFE 活性侵彻体在550 m/s 的撞击点火过程[104]Fig.21 The typical impact-ignition process of Al/PTFE reactive materials projectiles with a velocity of 550 m/s[104]

5.4 基于自定义本构模型的冲击反应行为数值模拟方法

由于活性材料的非自持冲击反应特性不同于炸药的点火增长自持反应过程，基于反应动力学模型计算不同加载条件下的释能效率是目前研究较多的一种数值模拟方法[83,106].该方法通常假设活性材料的冲击诱发化学反应过程由冲击温度控制[22-23]，采用Arrhenius 模型描述固态物质反应动力学行为[107-108]：

式中：y为反应程度，也称反应效率；t为反应持续时间；A为指前因子；Ea为表观活化能；Ru为摩尔气体常数；f(y)为动力学模型函数.

动力学模型函数的表达式通常采用Avrami-Erofeevn维核/增长控制反应模型[23,109-110]：

式中模型中n为反应级数，由反应机制决定.

郑元枫等[111]建立了考虑细观结构特性的活性射流成型数值仿真模型，如图22(a)所示.提取Al/PTFE 活性药型罩在形成射流过程中每个Al 颗粒内部典型区域温度-时间曲线，结合Arrhenius 和Avrami-Erofeev 反应动力学模型，可对计算结果后处理，获得活性药型罩材料中典型时刻反应度分布结果(图22(b)).为了直接使用数值仿真软件开展活性材料的冲击反应行为模拟，任柯融等[83]将反应动力学模型以子程序的方式嵌入LS-DYNA 非线性有限元分析软件中，结合Mie-Grüneisen 状态方程获取冲击引起的压力和温度变化，进一步基于反应动力学模型将由温度控制的化学反应效率进行更新，初步实现了对活性破片撞击靶体反应过程进行了数值仿真计算[83].

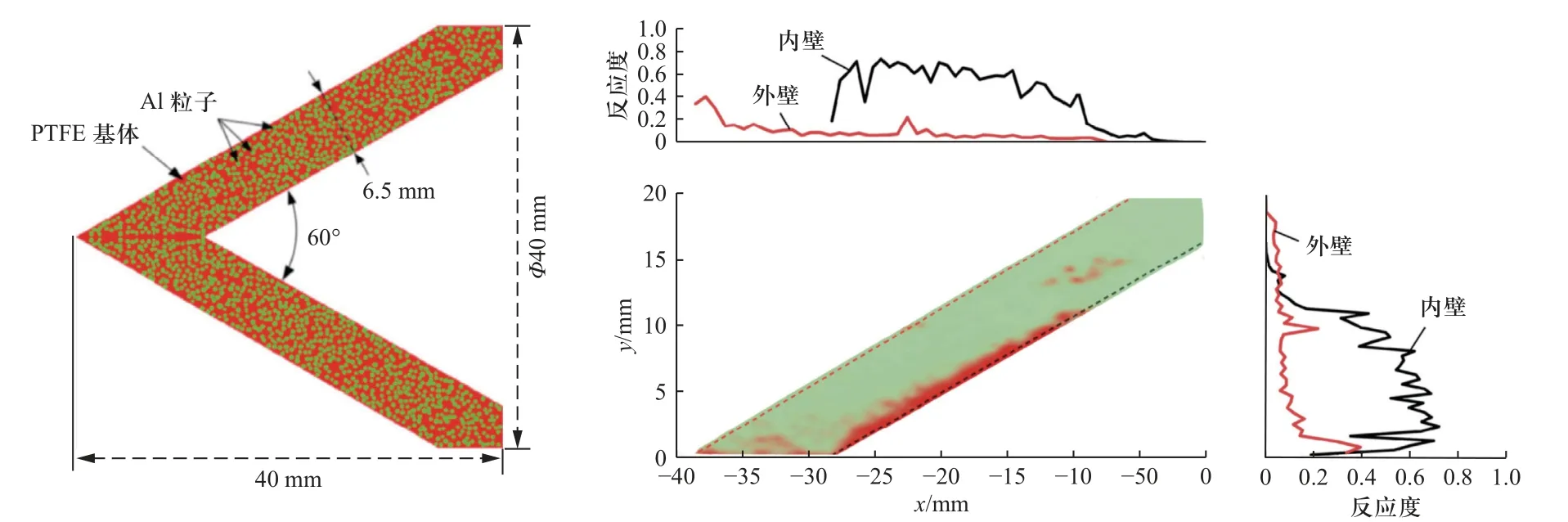
图22 考虑细观结构特性活性药型罩仿真模型和反应度可视化计算结果[111]Fig.22 The mesoscale model of reactive liner and visualization of reaction extent distribution[111]

为了更精细描述活性材料的非自持反应行为，卢冠成等[80]将Al/PTFE 的冲击反应过程分为两步：撞击点火和化学反应.其中，撞击点火主要对应活性材料的破碎和PTFE 的分解过程，后者由微孔塌陷产生的热点控制；而化学反应过程对应于Al 与PTFE 分解物之间的反应行为，由气-固反应模型进行计算，反应过程示意如图23(a)所示.在不考虑冲击反应行为的情况下计算Al/PTFE 长杆撞击钢靶后每个粒子产生的压力、失效参数，以此为输入量求得每个粒子的PTFE 分解度和化学反应效率，并可视化表征出来(图23(b)).

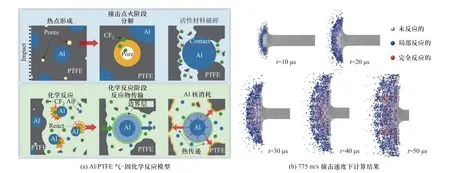
图23 Al/PTFE 气-固化学反应模型和775 m/s 撞击速度下计算结果[80]Fig.23 Impact ignition of gas-solid chemical reaction model for Al/PTFE and reaction morphology of Al/PTFE rods with the impact velocity of 775 m/s[80]

6 结 论

活性材料由于兼具结构强度和冲击反应释能特性而在高效毁伤和防护领域得到广泛的应用.活性材料的冲击反应机制及释能规律是该类材料设计与应用的重要基础科学问题，而复杂载荷下冲击反应及释能行为准确预测是推广其工程应用的关键技术.目前，研究人员在不同时空尺度建立了活性材料冲击压缩及反应行为数值仿真模型，揭示了活性材料宏观冲击动力学响应及化学反应行为与细观结构特性关联机制，同时发展了考虑反应弛豫时间和非自持反应特性的点火模型，基于火/炸药等含能材料本构模型对活性材料冲击反应行为进行了模拟，在相关数值仿真方法上取得了较大的进展.通过对现有研究工作的梳理，得到的主要结论和展望如下：

①活性材料分子动力学模拟和细观模拟工作主要集中于典型含能结构材料，如Al/Ni、Al/PTFE、Al/Fe2O3等复合材料.缺乏关于含能非晶合金和含能高熵合金冲击响应行为模拟方法的相关研究工作.下一步需结合材料细观结构特点重点构建势函数，同时进行细观结构表征，发展适用于该类材料的分子动力学模拟和细观模拟方法.

②关于活性材料冲击压缩特性细观模拟方法已较为成熟，但主要集中于密实态材料二维数值模拟上.获取活性材料真实三维结构特征及非密实材料孔隙几何形态特征，建立能反应真实细观结构的数值仿真模型是实现冲击压力、热点准确预测的重要发展方向.

③目前已基于不同扩散速率假设对活性材料细观尺度上的物质输运与化学反应过程进行描述，分析了不同加载条件下的活性材料冲击反应特性.后续研究中需进一步结合跨尺度模拟方法建立考虑细观结构特性的活性材料本构模型，为活性材料宏观反应行为的预测奠定理论基础.

④活性材料宏观冲击反应行为数值模拟主要基于火/炸药等含能材料本构模型，发展了反应激发与点火增长过程计算方法，但距离对活性毁伤元的毁伤效能的准确预测仍存在一定差距，亟待建立准确描述活性材料冲击加载条件下全时域响应理论模型，并基于此发展该类材料冲击反应行为高可靠性数值模拟技术.