基于群稀疏空间光谱总变分的高光谱混合噪声图像恢复

徐光宪,王泽民,马 飞

(辽宁工程技术大学电子与信息工程学院,辽宁 葫芦岛 125100)

1 引 言

随着高光谱成像传感器的不断发展,高光谱图像(HSI)提供了丰富的光谱信息,在分类[1-2]、超分辨率[3]和解混[4]等方面发挥着重要作用。由于高光谱传感器在采集数据时容易受到外界环境的影响,数据不可避免地会受到高斯噪声、脉冲噪声、死线和条带等各种混合噪声污染,从而降低了HSI的质量,限制了其后续的应用。因此,从已被噪声污染的HSI中恢复干净的HSI是很重要的。

近年来,鲁棒主成分分析框架(RPCA)[5]已被广泛应用于混合噪声的去除。通常,假设HSI沿光谱维数[4]具有低秩性质。同时,死线、条纹和脉冲噪声具有稀疏特性[6]。基于这些假设,Zhang等人的[6]首先提出了经典的低秩矩阵恢复(LRMR),用于HSI混合噪声的去除。此外,还采用低秩矩阵分解的方法进行了HSI混合噪声去除[7],以避免了奇异值分解的计算,提高了效率。由于基于低秩矩阵的方法需要将原始的三维HSI重塑为二维矩阵,会忽略了HSI的空间相关性。因此,许多算法引入基于低秩张量的方法来描述HSI的低秩特性。包括Tucker分解[8];和张量奇异值分解(t-SVD)[9]。然而,如文献[10]所示,低秩正则化并不足以描述HSI的先验空间信息。

总变分正则化是图像处理中保持局部空间分段平滑性常用的工具,因此,许多人提出了基于低秩张量分解框架的各种类型的总变分正则化模型,以同时探索HSI的空间和光谱先验。例如,在文献[11]中,将低Tucker秩模型和3DTV正则化项组合(LRTDTV)分别利用全局空间谱和光谱相关性,增强空间信息;如范等[12]将SSTV正则化加到低秩张量分解框架中(SSTVLRTF),使用张量核范数(TNN)近似HSI的低秩属性并同时利用空间和谱域之间的分段光滑性(SSTV正则项)来完成HSI去噪。然而,Tucker分解的不平衡矩阵化方法难以表征全局相关性[13];T-SVD框架在描述所有HSI模式的不同相关性方面缺乏灵活性,导致恢复性能次优。因此,Zheng等[14]将T-SVD推广到模kT-SVD,提出了纤维秩,并引入了凸代理(3DTNN)和非凸代理(3DLogTNN)来近似张量纤维秩。而在文献[15]中,Liu等直接约束解的张量纤维秩,并证明直接约束纤维秩与凸代理和非凸代理近似形式相比,更接近干净HSI的纤维秩。

因此,提出的FRTCSSTV算法也采用直接对张量纤维秩进行约束的方法来表示HSI的全局低秩,并同时利用群稀疏空间光谱总变分正则化,来增强空间信息。通常SSTV正则项采用L1范数范数对空间差分图像的稀疏先验进行正则化,但这些方法不能利用差分图像的共享行稀疏结构[16]。因此,提出的算法使用群稀疏正则化,用L2,1范数表示,来探索一个差异图像在两个空间维度上的共享稀疏模式,这与之前的SSTV正则化[12]完全不同。并将其嵌入到对应的低秩模型中,到达去除含有条带和死线的混合噪声。

将基于张量低纤维秩约束模型和群稀疏空间光谱总变分正则项结合在一起,对含有混合噪声的去除有很好的效果。具体来说,我们有以下两点贡献。

(1)直接采用张量低纤维秩约束模型并不能很好的去除含有条带和死线的混合噪声,因此,将其与群稀疏空间光谱总变分正则项进行了结合,增强了HSI局部空间信息和光谱维度的分段平滑性,来去除图像中含有的条带和死线噪声。

(2)为了求解该模型,我们采用了ADMM(交替方向乘子法)算法来获得全局最优解,实验结果表明,该算法易于收敛。并与其他模型相比,本文的模型能够取得更好的性能。

2 相关工作

HSI退化模型:被混合噪声污染的HSI数据用Y∈RM*N*p表示,其中M*N为空间域;p为谱带数。它们可以被建模为:

Y=X+S+N

(1)

其中,X∈RM*N*p为干净的高光谱数据;S∈RM*N*p和N∈RM*N*p分别为稀疏噪声和高斯噪声。

2.1 张量纤维秩

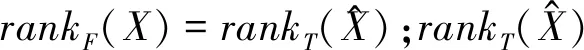
(2)

2.2 SSTV正则项

高光谱图像X的SSTV范数可以表示为[17]:

(3)

其中,Dh是水平方向上的差分算子,Dv是垂直方向上的差分算子,D是在每个像素的光谱特征上的一维有限差分算子。

而L1范数并不能反映HSI的群稀疏这一特征。L1范数只是要求所有元素的绝对值的和是最小的,没有对内部结构特性的进一步稀疏性要求。L2,1范数结合了L1范数和L2范数的优点,可以很好地描述HSI群稀疏的特征。一方面,L2,1范数可以保证梯度张量的光谱维数的每个管都是稀疏的。另一方面,也可以保证空间维数的稀疏性[18]。因此采用L2,1范数代替SSTV中的L1范数,新的SSTV可以写成:

(4)

2.3 FRTCSSTV模型

直接对张量纤维秩进行约束可以表征HSI全局的低秩性,而SSTV是一种研究相邻像素与相邻光谱波段相关性的局部模型。我们受到文献[12]启发,结合这两个互补的模型来恢复高光谱数据。综上所述,提出以下FRTCSSTV模型:

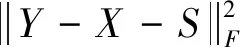
(5)

其中,λ,τ是一个调优参数;r是X的纤维秩的上界。

3 优化FRTCSSTV模型

通过ADMM算法引入辅助变量F,式(5)可以重写为:

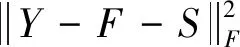
(6)

模型(6)的求解,可使以下的增广拉格朗日函数最小化:

s.t.rank(F)≤r

(7)

更新Fk+1:

(8)

由文献[15]中算法2可知,最优的张量纤维秩近似可由一个截断的T-SVD得到显式解,具体求解算法可参考文献[15]中算法2。

Fk+1=RT-SVD(Q,r,p1)

(9)

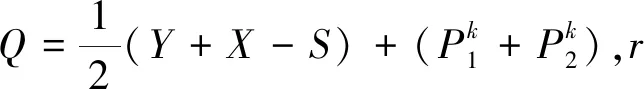
更新Xk+1:

(10)

式(10)可由ADMM算法求解,将上式改写为:

s.t.A=DhXD,β=DVXD

(11)

问题式(11)可分为以下3个子问题:

(12)

(13)

(14)

问题(12)、(13)可通过软收缩算子shrink(,)来解决。

(15)

(16)

在(14)中定义的子问题可以用一个迭代的最小二乘求解器来求解,如最小二乘QR分解方法[17,19]。

更新Sk+1:

(17)

更新拉格朗日乘子

(18)

综上所述,FRTCSSTV模型具体优化求解的步骤如算法1所示。

算法1:FRTCSSTV模型优化

输入:含噪声HSIY

输出:X,S

初始化X=S=F=P1=P2=P3=P4=0,

τ,λ,β,P,收敛条件ε

令k=k+1,迭代以下步骤

(1)通过(9)更新Fk+1

(2)通过(14)更新Xk+1

(3)通过(17)更新Sk+1

4 实验结果与分析

为了证明所提出模型的优势,分别对模拟和真实的HSI数据集进行了实验。实验中采取了3DTNN[14],3DLogTNN[14],FRCTR-PnP[15],3种模型来进行对比。为了方便数值计算和数据可视化,在恢复前,我们将HSI各波段的灰度值归一化。

4.1 模拟实验

模拟实验中,采用由反射光学系统成像光谱仪(rose-03)收集的Pavia城市中心数据集。Pavia城市中心数据集的一些光谱波段被噪声污染严重,不能作为去噪的参考。因此,去掉该数据的前几个波段,选取子图像的大小为200×200×80。由于模拟实验给出了地面真实度的HSI,采用了3个定量图像指标进行比较,包括各个波段平均峰值信噪比(MPSNR)、平均结构相似度(MSSIM)和光谱角度映射(SAM)。MPSNR越大,MSSIM和SAM越小,表示模型的去噪性能越好。

Case1:为了更接近真实场景下不同频段的噪声强度是不同的。我们对HSI每个波段加入不同强度的高斯噪声,高斯噪声的方差在[0,0.2]之间选取。在此基础上,在所有波段加入脉冲噪声。不同波段的脉冲噪声强度不同,其百分比从[0,0.2]选取。 然后在数据集的第44～54波段添加条带噪声。条带噪声的数量在20～40之间随机变化。

Case2:在Case1的基础上,在Pavia City Center数据集的38～48区也增加了死线。上述区域的死线数量在[3,10]之间随机变化,死线宽度在[1,3]之间随机变化。

(1)定量比较:在表1,表2中我们将性能最优值都加粗显示,可以看出,在这两种噪声场景下,该FRTCSSTV模型与其他3种模型相比具有更好的去噪性能;当模拟实验中加入高斯噪声、脉冲噪声和条带和死线噪声后,由于模型中的群稀疏空间光谱总变分可以更好的表示HSI的空间维度的稀疏性,图像中的条带噪声会被抑制;并且直接对张量纤维秩进行约束可以更好的保持HSI原有结构;所以该模型在去除混合噪声后各项指标都取得最优值。在表2中,MPSNR比FRCTR-PnP模型提升了1.4 dB左右;同时也保持了HSI原有的结构,MSSIM值也比其他方法更高;与其他3种模型相比SAM值也到达最低。为了更好显示实验结果,如图1所示,将Case2种每个波段的PSNR和SSIM值进行比较。从图中可以观察到,该模型在每个波段都能取得很好的PSNR和SSIM值;在噪声密集的地方,也能够稳定去除噪声,而其他3种模型都有很大的波动,对噪声的去除不是很理想。这证明了提出的模型去除这类混合噪声的优势。

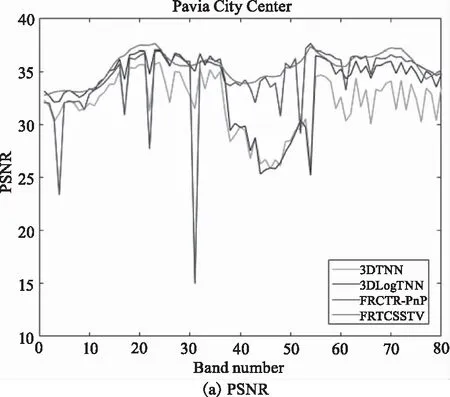
图1 Case2中不同波段的PSNR值和SSIM值

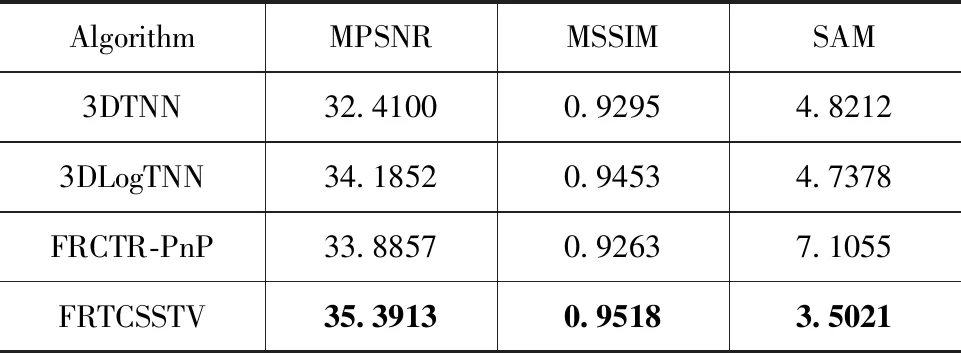
表1 Case1中定量数值评价结果

表2 Case2中定量数值评价结果

(2)视觉质量比较:由于该数据集具有很多波段,从中选取一个同时含有4种混合噪声的波段进行比较。如图2中第46波段所示,从图2(b)中不难看出,图像已经被混合噪声完全覆盖,观察不到图像的特征;通过不同的去噪方法后,噪声都被不同程度的去除。

图2 Case2中第46波段去噪效果对比

然而由图2(c)和2(d)可知,3DTNN和3DLogTNN方法去噪后图像仍会残留大量的条带和死线噪声。在图2(e)中,FRCTR-PnP方法去除了大部分混合噪声,但还有少量的条带噪声会影响视觉效果。在图2(f)中,由于群稀疏空间光谱总变分增强了空间的稀疏性,可以更好的去除条带和死线这类稀疏噪声,因此,去除噪声后的图像的视觉质量与原图像也最为相似,这也说明了该FRTCSSTV模型去除含有条带和死线的混合噪声的优势。

4.2 真实HSI数据实验

由于该模型对含有高斯噪声、脉冲噪声、条带和死线噪声4种混合噪声的去除具有很好的效果,因此,实验中我们采用了具有类似真实噪声的HSI数据集HYDICE Urban进行性能评估。与模拟实验一样,在测试恢复实验之前,将每个图像波段的灰度值归一化。不过在图4(b)、(c)、(d)中,仍然能看到一些条带噪声没能被去除,这说明了3DTNN、3DLogTNN和FRCTR-PnP这3种模型对去除条带和死线这类稀疏噪声具有局限性。然而,我们提出的FRTCSSTV模型不仅保持了HSI原有的结构,同时还增强了HSI的空间谱信息和光谱的分段平滑性,可以很好的去除这类噪声,并同时能保留原图像大部分的细节特征,这一现象表现出该模型对含有条带的混合噪声去除的优势。图3给出了4种不同方法对HYDICE Urban数据集第109波段的恢复结果。从图3(a)中可以观察到,采集到的图像已经被混合噪声污染,很难收集到有用的图像特征。如图3所示,经过各种方法去噪后,大部分噪声被去除,可以得到图像的一些特征信息。

图3 第109波段恢复图像比较

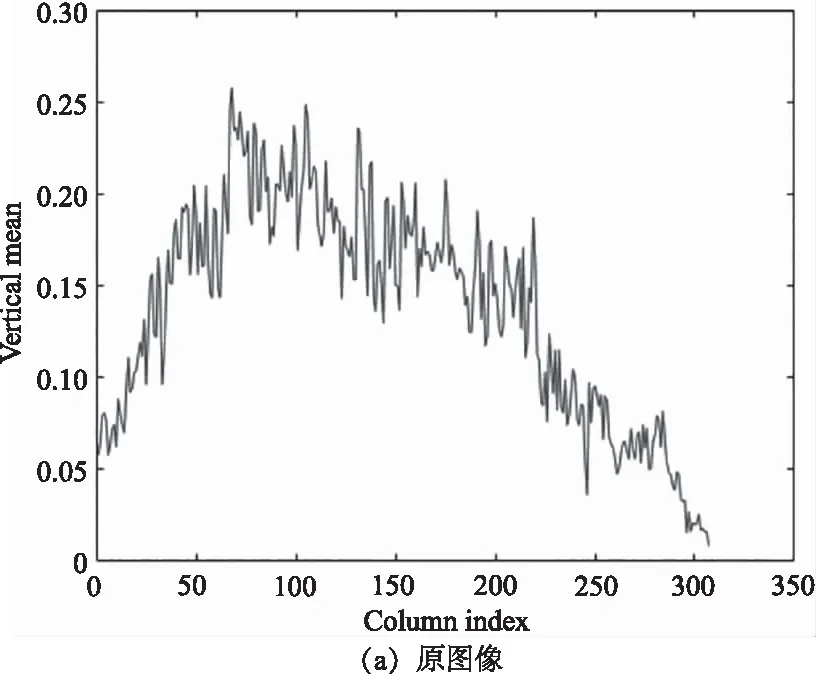
图4 第109波段垂直平均剖面比较

为了更好地显示该模型的去噪性能,如图4所示,我们将109波段去噪后图像的垂直平均剖面进行了比较。当平均轮廓曲线显著波动时,表明存在噪声。如图(a)所示,该图像含有大量噪声,经过去噪后,如图(b)、(c)所示,大部分噪声能够被抑制,但仍含有噪声未被去除。从图(c)中可以看到,虽然噪声被去除,但图像的轮廓曲线会过于平滑。如图(e)所示,提出的FRTCSSTV模型在去除混合噪声的同时,群稀疏空间光谱总变分正则项能够保留图像的细节特征,使轮廓曲线不会过于平滑,相比之下,得到了更好的结果。

5 结 论

提出的基于群稀疏空间光谱全变分正则化的高光谱混合噪声图像恢复的模型在去除含有条带和死线这类混合噪声的高光谱图像时具有很好的性能。该模型在模拟和真实数据的实验中,在去噪后的可以保留图像原有的结构特征和更多的细节特征,对条带等稀疏噪声有很好的抑制作用,在去除含有条带和死线的混合噪声方面与其他3种模型相比的更具优势。未来,也可以通过即插即用框架嵌入一些先进深度学习方面的去噪器[20-21],来提高去噪的性能。