基于LatLRR与NSP分解的红外与可见光图像融合

李云红,李嘉鹏,苏雪平,陈宇洋,刘杏瑞,谢蓉蓉

(西安工程大学电子信息学院,陕西 西安 710048)

1 引 言

不同类型的传感器对同一场景进行图像采集时,得到的采集图像因传感器的类型不同可描述不同的图像特征[1]。红外传感器利用物体的热辐射信息成像,红外图像中目标突出,热辐射信息明显,在恶劣天气环境下成像效果良好,但图像的细节信息、纹理特征缺失较为严重;可见光图像分辨率高且具有丰富外观信息,但其成像效果的优劣与目标场景的反射光线有关,易受天气、光照等因素影响,无法有效突出目标[2-4]。因此,将红外与可见光图像进行融合,结合二者的图像特征,得到目标更突出、细节更明显的融合图像,这对后续开展相关的图像处理工作具有一定的意义。红外与可见光图像融合目前已在机器视觉、航天、军事及电力等领域广泛应用[5-6]。

图像融合技术发展过程中涌现出许多方法,常见变换域基于多尺度(Multiscale Transform,MST)的融合方法有离散小波变换(Discrete Wavelet Transform,DWT)[7],非下采样轮廓波变换(Non-Subsampled Contourlet Transform,NSCT)[8],该方法通过非采样金字塔滤波(Nonsubsampled Pyramid,NSP)完成图像的多尺度分解[9]以及双树复杂小波变换(Dual-tree Complex Wavelet Transform,DTCWT)[10]等。除此之外,还有其他方法,如基于多分辨奇异值分解法(Multi-resolution Singular Value Decomposition,MSVD),该方法用奇异值分解代替小波变换中的高通有限脉冲响应滤波器,与小波变换相比没有依赖数据集的固定基向量集,计算简单便于应用[11-12]。在目标增强多尺度融合算法[13]一文中,给出了一种非线性变换的融合思想,使该法与传统MST融合算法相比,融合图像对比度有了明显的增强。文献[14]则提出了一种梯度转移和总变差最小化的融合方法(Gradient Transfer Fusion,GTF),具体来说,该方法可以调控红外图像像素强度及可见光图像梯度特征的权重,但此法易造成可见光图像细节特征的丢失,最终的融合效果并不令人满意。而文献[15]利用Bayesian回归模型的思想,提出了一种分层Bayesian模型,该模型可实现融合权重的自适应,使融合权重的设置变得不再困难,但该法对融合图像红外特征保留较少。低秩表示(Low Rank Representation,LRR)[16]的提出,实现了数据全局结构信息的提取,但不能保留数据局部结构信息,在LRR的基础上,文献[17]对LRR方法进行了优化,提出了潜在低秩的表示方法(Latent Low Rank Representation,LatLRR)。与LRR相比,LatLRR能捕捉到图像的局部结构信息,使图像信息更为丰富。文献[18]则通过LatLRR对源图像分解,并采用加权平均策略进行低秩部分的融合,但易使图像全局结构信息部分丢失,导致最终融合重构图像质量不佳。文献[19]提出一种多级的LatLRR图像融合框架MDLatLRR,该方法提取了图像多级显著性信息与全局结构信息,在融合效果上有所改善。

针对上述融合算法图像对比度低、红外特征不明显的问题,论文提出了一种结合LatLRR与NSP的分解模型,并在局部结构信息及低频信息融合时选择不同策略,然后通过非线性变换函数调节重构权重比例。该方法使最终融合结果图像既有红外图像特征又有可见光图像的信息。将论文算法与DTCWT、MSVD、Bayesian、LatLRR 及MDLatLRR算法进行对比,验证了论文算法的有效性。

2 相关理论

2.1 LatLRR理论

LatLRR分解[18]这一理论的精髓在于将原始数据(待分解图像矩阵)分解为独立的三个部分:全局结构层、局部结构层、噪声信号,其分解的数学表达如式(1):

W=WQ+RW+E

(1)

式中,W是待分解图像矩阵;Q是全局结构系数;R是局部结构系数;WQ是全局结构层;RW是局部结构层;E是噪声信号。

为寻求最优LatLRR分解,将(1)式的求解转化为式(2)的数据联合最小化问题。

(2)

2.2 NSP原理

NSP是经典MST方法NSCT中图像的尺度分解方法[8-9],可以通过NSP来提取源图像的低频信息。通常由于输入信号的平移使轮廓波变换系数增大,造成输出图像的吉布斯效应,而NSP在处理信号时,并未进行降采样,消除了吉布斯效应对输出图像的影响,其尺度分解由双通道式NSP实现,具体结构如图1所示。该模型包含分解滤波器{Hi(z)}i=0,1及合成滤波器{Gi(z)}i=0,1,NSP满足Bezout恒等式:

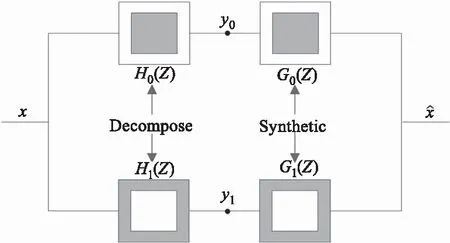
图1 双通道式NSP模型

H0(z)G0(z)+H1(z)G1(z)=1

(3)

式中,H0(z)、G0(z)分别是低通分解及合成滤波器;H1(z)、G1(z)分别是高通分解及合成滤波器;G0(z)、G1(z)值为1;H0(z)+H1(z)=1。

NSP经过1层的分解后,生成低频高频子带图像各1个,各子带图像均与输入的分解源图大小相同。

3 融合算法

融合算法的整体流程框架如图2所示,该算法分3步进行,具体操作包括:(1)分解,红外图I,可见光图V分别经过NSP、LatLRR分解后,提取各自的低频部分Ia(x,y),Va(x,y),局部结构部分Ib(x,y)、Vb(x,y);(2)融合,对低频部分Ia(x,y)、Va(x,y)采取一种红外像素强度权重调控的策略进行融合,生成低频融合图像N′f(x,y),对局部结构部分Ib(x,y),Vb(x,y)采取传统求和策略进行融合,生成局部结构融合图像Mf(x,y);(3)融合图像的重构,对低频融合图像N′f(x,y),局部结构融合图像Mf(x,y)使用非线性变换法进行重构,最终得到融合结果图像U(x,y)。

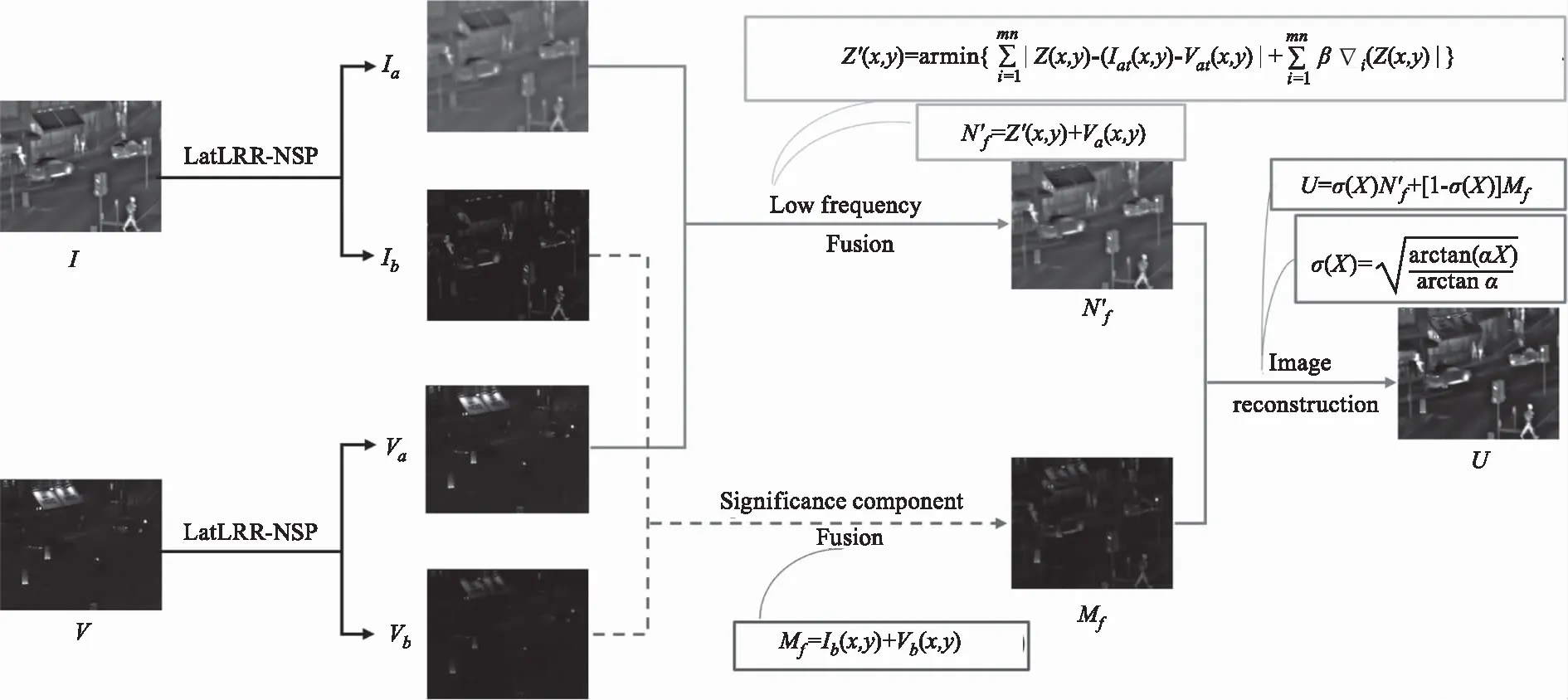
图2 融合算法整体流程

3.1 图像的分解

图像全局结构信息与其低频信息所表征的物理意义相同,即均用来反映图像的主体概况、像素强度等重要特征。与之相同地,图像的局部结构信息与其高频信息均可用来表征图像具体细节特征。融合任务中,使用现有LatLRR方法对源图像分解时,必须在线求解图像对应全局结构系数。为了避免图像全局结构系数的在线求解,对算法运行效率的影响,在图像分解时,采用一种基于LatLRR-NSP相结合的分解方法。以源红外图像分解为例(见图3),预处理后,通过LatLRR获得局部结构系数映射矩阵L,然后直接提取源图像局部结构信息,同时,引入NSP的1次分解,获取与全局结构信息表征含义相同的低频信息。在避免全局结构系数在线求取的同时,结合NSP分解所得良好的图像低频信息,完成源图像的分解。

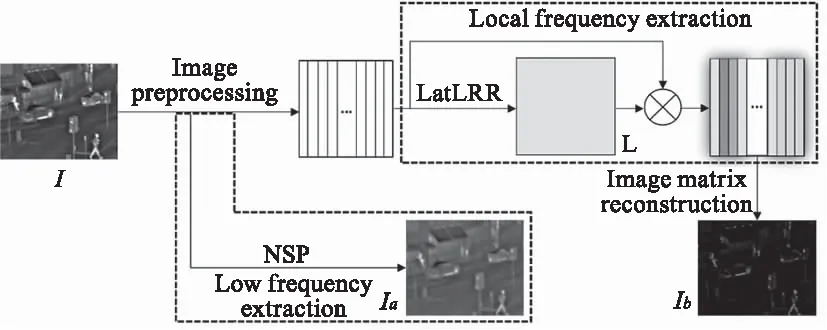
图3 基于LatLRR-NSP的分解过程

3.2 低频部分融合

红外图I,可见光图V通过分解后,所得到的低频分量部分反映了二者图像像素强度的基本灰度等级。低频部分的融合为:

Nf=ξ(Ia)+βξ(Va)

(4)

式中,Nf是低频融合结果;ξ(Ia)、ξ(Va)分别是红外低频与可见光低频的约束分量;β是低频融合平平衡系数,用来对低频红外像素的权重进行调整。

红外低频分量Ia(x,y)中,目标对象与背景间的像素强度差异远远大于可见光低频分量Va(x,y)。红外低频分量图像与可见光低频分量图像相比具有明显的可见性,即更容易在红外低频分量图像中发现目标对象。因此,在低频部分进行融合时,应尽可能应使融合图像的像素强度保持低频红外分量部分的像素强度分布。从而,低频融合结果Nf(x,y)与红外低频分量Ia(x,y)之间的约束分量ξ(Ia)的范数应尽可能小。

(5)

式中,Nf是低频融合结果;Ia是红外低频分量。

可见光低频约束分量ξ(Va)重点是对低频融合图像Nf(x,y)在梯度进行约束,将可见光低频分量Va(x,y)图像的丰富梯度信息反映在低频融合图像Nf(x,y)中,使ξ(Va)约束项达到最优化。

(6)

低频融合结果应保留红外分量的像素强度,这意味着Nf与Ia的差趋近于0,因此,Nf与Ia间的差应为拉普拉斯分布。同时在低频融合时,Va梯度量转移到Nf的过程中使图像部分平滑,这导致了梯度变换的稀疏性,因此,通过L1范数实现最小化梯度差进行优化。文献[20]指出,拉普拉斯分布对应的L1范数能更好地进行数据拟合。将约束项(5)、(6)中的q、p均取值为1的L1范数。对式(4)进行优化。

令Z(x,y)=Nf(x,y)-Va(x,y)可得:

(7)

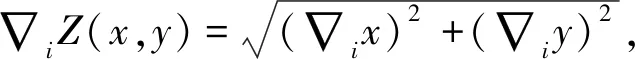
完成上述优化后,低频部分最终融合策略模型可表述为:

(8)

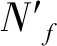
3.3 局部结构部分融合策略

LatLRR可以从源图像中提取局部结构信息。对红外局部结构部分Ib(x,y)与可见光局部结构部分Vb(x,y)采取传统的基于像素灰度值求和的策略进行1∶1融合。

Mf=Ib(x,y)+Vb(x,y)

(9)

式中,Mf是局部结构融合结果;Ib(x,y)、Vb(x,y)分别为红外、可见光局部结构部分。

以1∶1进行融合,这是由局部结构部分所包含的图像局部结构信息所决定的。图像局部结构信息用来衡量图像的细节、纹理等信息,在对其进行融合时,往往需要把红外与可见光图像的局部结构信息进行加和,以保证融合结果中既有红外特征又有可见光特征。

3.4 融合重构策略

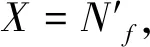
(10)

式中,X为低频部分;α为非线性平衡系数,取值范围(0,∞)。

不同图像的低频部分与局部结构部分的像素强度、细节特征均有差异,通过调整非线性平衡系数α来完成重构图像各分量的权重占比。图4给出了α取值对σ(X)影响的非线性曲线,当α的取值越大,低频部分与局部结构部分权重差值越大曲线越陡,反之则越小,曲线较为平缓。实际应用中,可对不同图像进行有针对的调整α,达到最优重构效果。

图4 α取值对σ(X)影响的非线性曲线

最终融合重构结果表示式为:

(11)

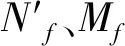
4 实验部分

实验在公开数据集TON与M3FD中选取4组(各两组)已配准的红外与可见光图像进行实验,图5前两列和后两列分别为选取的TON数据集图像及M3FD数据集图像。将本算法与DTCWT[10]、MSVD[11]、Bayesian[15]、LatLRR[18]以及MDLatLRR[19]算法进行对比,不同算法结果对比见图5。实验平台及配置:Windows 10操作系统,MATLAB R2018b,CPUi5-11260H,处理器图像NVIDIA GTX3050,内存16 GB。

图5 实验所用红外与可见光图像

本算法的参数设置具体在低频融合平衡系数β及融合重构时非线性平衡系数α。

β与α的不同取值,分别对低频红外像素权重、局部结构信息与低频信息在融合结果的占比以及相关评价指标有一定的客观影响,二者的取值会对整体融合效果的优劣共同作用,所以,在进行对比实验前,应确定β与α具体取值。

图6为本算法在4组融合结果图像上,β与α取6种不同值时,在互信息(MI)、信息熵(IE)、像素特征互信息(FMI_pixel)、标准差(SD)及视觉保真度(VIF)5种指标上各自的平均值,当β与α取值为2时,算法在MI、IE及VIF指标上取得优势。SD指标相对较好,FMI_pixel指标数据较为平稳。

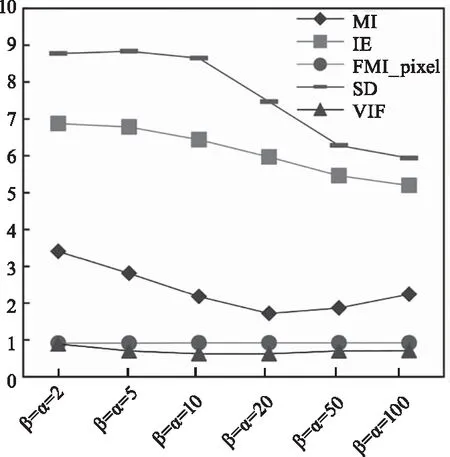
图6 不同取值β与α在4组融合图像上指标平均值曲线

图7则是β与α取值为2、5、10、20、50和100这6种不同值时,算法的融合结果图像,从主观角度来看,当β与α取值增大,融合结果图像的红外特征越来越弱,尤其是在β与α取值为100时,肉眼已经几乎无法在观察到融合之前的源红外图像的具体特征。随着β与α取值的不断增大,尤其是在左下角人物和画面中汽车的轮胎部分的红外特征减弱趋势最为明显,β与α取值为5、10、20、50和100时,均没有取值为2时显著。在β与α取值为5、10和20这3个值的图像中,图像整体较为模糊,图中的细节信息很难察觉。综合图6的客观指标与图7的成像效果,β与α值为2时,融合图像的视觉感知效果相对较好,为保证融合结果图像的定性与定量的优势,故将β与α设置为2。

图7 不同取值β与α融合结果图像对比

对比算法参数设置:MDLatLRR方法level设置为1,其余对比算法参数均按原文献设置。

4.1 主观评价

图8 Group 1中,我们可以看到Bayesian方法的图像画面整体呈现模糊的视觉效果,对比观察画面中左上方坐姿人物以及右下方站姿人物,虽然所对比的5种算法可以看到目标人物,但其目标人物的图像亮度均没有本文算法融合结果的亮度高。在Bayesian方法的结果图像中,目标人物的边缘较为模糊,且画面中的车辆与人物界限不清,较难分辨,而本文算法对画面中目标人物边缘清楚与背景的对比度远高于其他算法,在图像整体较为黑暗的情况下可以清楚的分辨目标人物与车辆以及背景,有利于黑暗场景的目标识别。

图8 不同算法结果对比

图8 Group 2中,DTCWT方法结果图像整体有较为明显的重影,尤其是在房屋侧面的这一部分,我们能清楚的观察到这一现象,图像的整体存在一定失真。在MSVD与MDLatLRR方法中,几乎没有重影,但在画面主体卡车的轮胎部位对红外特征保留较少,而Bayesian方法的融合结果图像车辆轮胎模糊不清,无法观察到轮胎的轮廓,画面整体模糊。本文算法产生的融合结果图像,在所对比的4种算法中红外特征最为明显,并且在车辆轮胎部位能清晰的显现轮胎的轮廓,保留了一定的可见光信息。

图8 Group 3中,所对比5种融合方法的融合结果图像灰度值较低,且融合结果图像均在不同程度上对红外部分的细节的处理效果差于本文算法。在各个图像中,近景的车辆与道路上的行人均清晰可见,但在画面的远景部分,本文算法的融合结果图像对源红外图像画面中远方的两个细长型目标物体这个细节部分保留清晰,而所对比的5种算法中,Bayesian方法最为不明显,其余方法的视觉效果均没有本文算法保留的效果好。

在图8 Group 4所对应的源红外图像中能够看到,图像的左上方有一个摄像头,源图中摄像头本身较为模糊。图8 Group 4中,各个算法的融合结果图像的左上方红框部位均保留了源红外图像中摄像头这个目标,但经过比对,各对比算法的融合效果的对比度均没有本文算法融合效果佳。

4.2 客观评价

在对图像融合的效果进行评价时,除了主观评价外,定量的评价也尤为重要。

通过采用信息论:互信息(Mutual Information,MI)、信息熵(Information Entropy,IE)、像素特征互信息(Feature Mutual Information of pixel,FMI_pixel);图像特征:标准差(Standard Deviation,SD);人类视觉感知:视觉保真度(Visual Fidelity,VIF)3大类的5种指标[21],对本次实验结果进行综合全方位的客观评价。Group 1～Group 4融合结果图像的评价指标数据,如表1所示。

MI是对融合结果图像在源图像保留信息量多少的度量,MI越大,保留信息越丰富;IE的大小可反映图像信息量的丰富程度,其值越大融合效果越佳;FMI_pixel用来衡量融合结果图像与源图像之间基于区域像素的互信息量,其值越大越好;SD代表图像的灰度分布,SD越大融合结果图像对比度越高;VIF用于衡量融合结果图像整体图像质量信息保真度,指标数值越大,图像质量越好。由表1可知,在Group 1、Group 2和Group 4这3组数据中,本文算法在5种评价指标中的MI、EN、SD和VIF这4种指标优于所对比的其他5种算法,特别是在MI与EI这两个指标上,本文算法的指标数据明显高于其他算法。

为更加客观通过指标数据比对算法的优劣性,对使用5种不同对比算法和本文算法产生的Group 1～4这4组不同场景和风格的融合结果图像的5项指标数据分别求其平均值,用平均值表征各指标的整体数值差异,见表2。本文算法5项评价指标中,在MI、IE、SD和VIF数值均高于其他对比算法,而FMI_pixel指标由于实验图像之间的像素差异,使该指标总体平均水平较低。再结合主观定性评价,本文算法能很好利用LatLRR与NSP的特性,并在适当融合策略作用下,使融合结果图像在红外特征上得以增强,对可见光特性也有一定保留,从主观客观上证明了本文算法优越性。

表2 组1～组4融合结果图像评价指标平均值

5 结 论

本文提出了基于LatLRR与NSP分解的红外与可见光图像融合算法,该算法模型很好地结合了LatLRR与NSP在图像分解时的优势,更好地获取了源图像分解产生的低频信息与局部结构信息。在图像融合步骤中,针对低频及局部结构信息的特点,分别采取了不同的融合方法。融合算法的最后,对图像进行重构时添加了非线性变换函数,算法整体实现了融合结果图像在视觉效果上以红外特征为主,同时,与源红外图像相比,其外观细节等特征更加明显。通过在公开数据集的实验,从定性定量两个方面分析验证了本文算法的有效性、稳定性。