面向大口径地基望远镜视宁度检测方法综述

赵文栋,杨 飞,安其昌

(1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)

1 引 言

光的应用领域包括武器、测距、遥感、目标指示、自适应光学等。然而,所有利用可见光学或红外波的系统除了考虑与波本身相关的效应之外,还必须考虑与波在其中传播的介质相关的一般传播效应。在大多数情况下,传播介质是湍流大气,沿传播路径的微小折射率波动会对波产生各种不利影响。

光波在大气中传播时会受到大气折射率波动的影响,而大气折射率的随机波动与微观温度波动直接相关,微观温度波动是由风和对流引起的空气湍流运动引起的。传播中的光波会穿过大量的折射率不均匀体,因此它们对光波的累积效应相当深远。折射率波动导致恒星闪烁,限制了天文望远镜在几秒弧内分辨小物体的能力。而折射率波动导致的光波偏转是影响激光发挥效能的重要因素。因此,研究如何量化并测量这些影响,便成了大型望远镜以及激光大气传输领域需要解决的问题[1]。

2 视宁度及其量化

2.1 视宁度形成

视宁度效应是由大气湍流引起的,通过大气湍流,来自恒星的一些光被折射不均匀性散射。当光波在湍流大气中传播时,它会经历振幅和相位的波动。通过聚焦该波形成的图像表现出强度、清晰度和位置的波动,这通常被称为闪烁、图像模糊和图像运动[2]。

对于望远镜来说,在整个大气的湍流引起的视宁度现象中,根据作用湍流的位置不同,视宁度可以大致分为大气视宁度、圆顶视宁度以及镜面视宁度三种类型[3-5]。

2.2 视宁度量化

在量化视宁度方面,通常使用大气折射率常数、大气相干长度、大气相干时间以及格林伍德频率等参数,其含义为:

大气相干长度或弗里德参数r0,定义为衍射受限的圆形瞳孔的直径图像和视觉受限图像具有相同的角分辨率。其可表示为

(1)

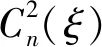
大气相干时间τ0,在时间间隔τ0内,湍流位相变化量的 RMS值为1 rad。大气相干长度与大气相干时间有

τ0=0.314r0/ν

(2)

格林伍德频率fG[7],物理含义为畸变波面上高于该频率的位相功率谱的 RMS值为1 rad。格林伍德频率与大气相干时间有

fG=0.134/τ0

(3)

视盘半高全宽(FWHM)星图轮廓半高处的角直径,一般称为点扩散函数(PSF)

斯特雷尔强度比,实际图像的PSF峰值高度与理想衍射极限图像。

3 视宁度检测技术

视宁度使光线产生偏转和闪烁。从无限远处的点光源通过系统传播的波前会受到到达角和表面亮度的扰动。到达波前中的角偏转与闪烁的比率是沿光源的视宁度发生波前退化的指示器。

在平面波中产生闪烁的小角散射和折射需要相当大的传播距离来积累足够的多径干扰,以产生表面亮度的显著波动。测量闪烁的横向空间尺度以推断到扰动的距离是各种闪烁视宁度测定系统的基本原理。

相比于闪烁,短距离效应不会抑制光束的偏转。平面波中引入的任何波前倾斜都会在焦平面上产生相同的图像运动,而不管它出现在哪里。这表明图像运动对于测定局部视宁度方面可能比测量闪烁更有效,而测量波前倾斜是确定焦平面上的PSF的更直接的途径,使用它来计算光束偏转和图像运动统计是最广泛的方法。

因此,在视宁度检测方面,主要分为三个学术流派,分别是计算流体动力学模拟,测量强度闪烁以及测量图像偏移,并应用于各类视宁度检测中。

3.1 大气视宁度检测方法

现代的大型光学望远镜,其安放的位置对于功能的发挥起着重要的作用。大气视宁度检测技术的发展将不仅为天文台址的选择提供参考依据,而且还可为自适应光学系统的设计、大气光通讯技术等光学工程应用提供支持,也为大气湍流理论研究提供宝贵的基础数据[6]。

3.1.1 闪烁探测和测距技术(SCIDAR)

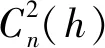
图1 G-SCIDAR技术原理图[8]

Habib 等人提出了一种称为单星闪烁探测技术(single star SCIDAR,SSS)[10]的新方法,该方法利用单星闪烁来反演大气湍流参数。该仪器不使用 GS 双星技术的大口径望远镜,而只需要一个 40 cm口径的望远镜。

图2显示了SSS的原理:每个湍流层在望远镜光瞳上创建一个大气散斑图案,它以相应层的速度移动。v是该层的速度,t是两个连续层之间的时间间隔。那么两个图形之间的距离d=vt。为了测量d,我们计算在不同时间t=nδt拍摄的独立闪烁图像的互相关,其中n=1,2,3,…δt是两个连续帧的间隔。通过计算空间自相关和不少于两个时空互相关图像,实时分析闪烁图案。

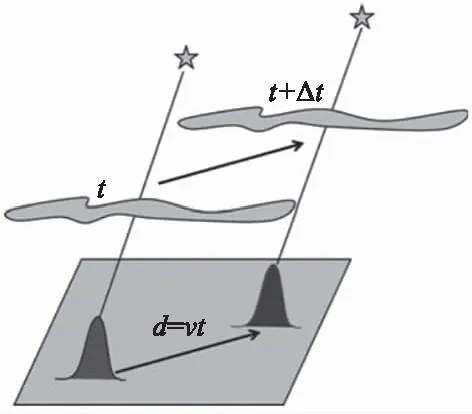
图2 单星闪烁探测技术原理图[10]

3.1.2 多孔径闪烁仪(MASS)

MASS(多孔径闪烁传感器)仪器由一个14 cm的离轴反射望远镜和一个探测器单元组成,该探测器单元使用光电倍增器测量望远镜光瞳四个同心区域中单颗恒星的闪烁。四个同心孔的标称直径选择为2、3.7、7.0、13 cm,MASS模块光学布局如图3所示。

图3 MASS模块光学布局[11]

恒星的光经由望远镜进入探测装置。入射光从折叠式反射镜1反射时,穿过安装在由步进电机控制的盘2上的聚焦孔径。法布里透镜4以大约20的缩小因子在分割器7上形成望远镜光瞳的图像。分割器由四个不同倾斜度的同心反射镜组成,每个反射镜以一定角度反射光束。内镜的直径为1 mm,外镜的直径为6.5 mm(分别为2 cm和13 cm,投影到望远镜光瞳上)。四个反射光束落在球面镜3A～3D上,球面镜3A～3D在PMTs A、B、C和D的光电阴极处对光瞳重新成像。二向色分束器5将波长在600 nm以上的光反射给检测结构,该结构由折叠式反射镜8、透镜9和目镜10组成,10处可放置CCD相机来接收图像。检测光经由胶合到分束器的玻璃滤光器6进行光谱过滤[11]。

3.1.3 差分像运动测量法(DIMM)

现如今,在量化天文视宁度领域,最普遍的方法是差分像运动测量法(DIMM),其概念是由Stock &Keller 于1960年提出,并由Sarazin &Roddier于1990年描述了它的现代实现[12-13]。其原理如图4所示,CCD通过两个子孔径将光线聚集到相聚在x的两个点上,探测经过大气后畸变的波前[12]。大气畸变波前经由两个子孔径探测后,成像在CCD上。短曝光CCD帧上的两个图像的坐标应用中心算法确定。得到坐标后计算径向、横向方差,结合湍流模型来计算视宁度。

图4 传统DIMM的原理图

用于从图像运动方差计算视宁度的公式如下所示:

(4)

(5)

其中,λ为成像波长。常数K取决于孔径间距B与其直径D的比值。

实际上,DIMM真正测量的是Fried参数r0,传统上用视宁度来表示。使用正确的公式将r0从图像运动中导出,计算和观察,并预测大型望远镜中的图像移动的大小,能够实现10 %或更高的绝对精度[13],因此,DIMM是一种简单而可靠的测量视宁度的方法。

3.2 圆顶视宁度检测方法

除了大气视宁度影响天文观测的分辨率以外,由天文建筑结构引起的圆顶视宁度的影响也不可忽视。如果天文建筑设计不当,造成的圆顶视宁度可能会比整层大气造成的像质衰减还要严重,也无法体现出好的天文台址和望远镜的效力。因此,圆顶在设计时,应该考虑采取措施减少圆顶视宁度的影响[14]。一些大型望远镜常使用计算流体动力学(CFD)建模来指导圆顶设计和建立要求,如TMT,LSST,Rubin,GM等。在实际检测方面,除了传统的DIMM外,还使用圆顶视宁度监视器和闪烁仪等设备进行检测。

3.2.1 计算流动体力学

首先对圆顶结构进行模拟,然后在有通风口的情况下重复进行模拟。此外,对于一些望远镜,要考虑其外部影响,如LSST 望远镜[16]、Keck II望远镜[17]等,在建模时,考虑被动通风、围护结构构造和地形对光学性能的影响。因此,其计算流体动力学模型包括望远镜场地的当地地形、建筑和内部有望远镜质量模型的圆顶,还包括辅助建筑在内的外壳几何形状,LSST计算流体动力学模型如图5所示。

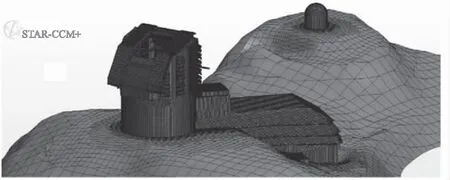
图5 LSST计算流体动力学模型[16]

使用计算流体动力学来估计由于圆顶观测引起的光学湍流和图像质量下降的一般方法如下:首先,运行模拟两次流通时间(2FT),冲洗初始条件,以给定的采样速率在相应的光路网格上保存瞬时温度/速度足够长的时间。然后,计算湍流统计,对于每个时间步长,计算光程长度(OPL),将其折叠为 2D OPD,然后移除活塞,标称OPD坐标为20482。由于初始OPD的分辨率与CFD分辨率相当(0.25～0.5 m),根据给定的频谱分布选择增加高频分量。对于每个时间步长,计算光学传递函数(OTF)和观察时间的平均值。将其乘以大气调制传递函数(MTF,根据给定r0的Kolmogorov大气结构函数计算,名义上为 0.2 m×0.5 m)。最后,计算PSF和FWHM。

目前,计算流体动力学的方法,被广泛应用于大型望远镜圆顶的设计与优化。数值方法与可视模型相结合,可以提供对复杂问题的关键见解,如外壳和镜面的被动通风,并成为下一代超大型望远镜[18](如TMT)的有用设计工具。

3.2.2 圆顶视宁度监视器

相比于大气视宁度,圆顶视宁度很难量化。因此,需要可靠的圆顶观测测量来优化圆顶通风和温度控制,以最小化圆顶视宁度对成像质量的影响。Blanco望远镜[19]为此目的开发了圆顶视宁度监视器,基于测量自准直光束的到达角波动,对圆顶内的湍流进行采样,用以得到视宁度。

该设备的基本原理,是使用一个激光二极管,发出准直光束,并在圆顶内传播,当光线被安装在一个可调节倾斜度的运动支架上平面镜反射回来后,由相同的光学器件聚焦到电荷耦合器件上。此时,湍流产生的像移是单次传播的两倍。圆顶视宁度监视器原理图如图6所示。

图6 圆顶视宁度监视器原理图[19]

该仪器于2017年9月安装在位于塞罗托洛洛4 m的Blanco望远镜上。10 m长(图7(a))的传播路径平行于望远镜轴,带有第一面镜子的试管(图7(b))连接到镜子单元,第二面镜子(图7(c))装在一个盒子里,夹在白色圆形光束上[19]。它从反射镜单元的边缘开始,在那里与第一反射镜通过接口板连接。通过调整第一面M1镜的倾斜角度,使光束在M2中心,并覆盖一张白纸。然后M2被调整以将光束返回到M1。之后,针对返回光束和发射光束的空间重合对调整进行细化。为此,用一张带有2 cm洞的纸挡住出射光束,然后,通过轻微调整M1镜,返回的2 cm光束在纸上的轨迹可以在这个孔的中心。最后,通过观看实时全帧图像来确定光斑的中心,调节激光电流以避免所选曝光时间的电荷耦合器件饱和。

图7 Blanco望远镜的圆顶探测器安装

3.2.3 闪烁仪

为了监测 Keck II 望远镜圆顶环境中的大气湍流,部署了一台光学 Scintec SLS20(A)闪烁仪[17]。图8为Keck II上闪烁仪的位置布局。闪烁仪发射器与双通道探测器并排放置,并支撑在M1镜室结构中。实线和分段线表示光信号从发射器A到最远处的后发射器C,并返回检测器A的路径[17]。

图8 Keck II上闪烁仪的位置

值得注意的是,闪烁仪4信号穿过了湍流两次,一次是在到达折叠式反射镜的途中,另一次是在返回检测器的途中。这表示,在整个信号路径中,检测到的信号强度变化具有两次穿过相同湍流的特征。因此,在折叠路径中观察到的信号强度变化是沿着相同长度的非折叠路径观察到的强度变化的两倍。

3.3 镜面视宁度检测方法

地基式天文望远镜运行时,望远镜镜面与空气有温差并在镜面前方的光路中产生的空气湍流,空气湍流的存在引起空气密度和折射率变化使得光波波前改变,地基式天文望远镜受镜面空气湍流影响而产生的像质衰减程度称之为镜面视宁度。

3.3.1 62 cm镜面视宁度检测

在镜面视宁度检测方面,Iye等人进行了各种实验。在东京的日本国家天文台,Iye等人用62 cm的反射镜装置进行了一次镜面视宁度观测实验[19],该装置最初是为了验证一种新的主动光学系统的可行性而设计的。

测试装置如图所示:主镜是62 cm直径的Pyrex玻璃镜,为球面弯月形,厚度为2.1 cm,曲率半径为300 cm,带有内部光源的Shack-Hartmann波前分析仪位于反射镜曲面的中心。使用CCD照相机作为波前分析仪的检测器,测量放置在望远镜出瞳处的微透镜阵列产生光斑分布。用二分法测量这些光斑的质心,其精度为0.05像素,以评估波前像差。若存在视宁度退化,则图像质量通过以下表达式评估斯特雷尔比率来表示:

(6)

其中,σω是测得的波前均方根误差。然后,通过用于分析镜像质量的计算机程序将斯特雷尔比值转换为FWHM视宁度值。

镜面没有被主动加热或冷却,但是它的温度和周围空气的温度遵循不同的日变化周期,因此大多数时间都存在镜子-空气温差。为了测量强制通风的效果,镜子的上表面被带有导流喷嘴的电风扇产生的气流冲洗,如图9所示。

图9 62 cm镜面视宁度检测布局[19]

最终,通过Shack-Hartmann照相机定量测量由于镜面温度差产生的对流引起的波前扰动。在90多个昼夜的各种条件下进行了大约60000次测量,评估了具有高统计精度的镜面视宁度的定量特征。

3.3.2 4cm镜面视宁度实验

Zago在1997年提出了一项实验来测量镜面视宁度[20]。实验描述为:一束直径为3 cm的平行激光束,照射在直径为4 cm的水平平面镜上,发生反射,并聚焦在位置感测检测器PSD上,实验的光学示意图如图10所示。镜面使用自粘薄膜电阻加热,以产生温差,从而产生视宁度。该视宁度由PSD上图像运动的RMS进行评估,并根据等效FWHM角进行转换。

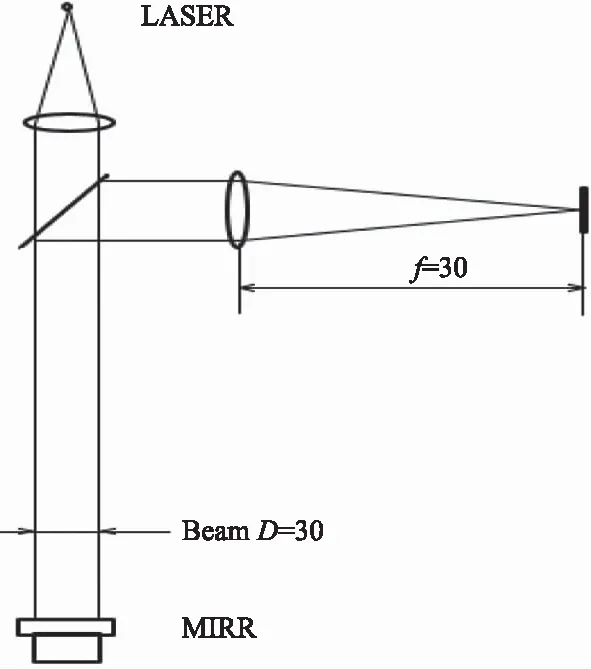
图10 4 cm镜面视宁度实验光学示意图[20]

σ2=0.35λ2D-1/3r0-5/3

(7)

其中,λ是波长,在该实验中是680 nm,D是3 cm的光束孔径。在此实验中,PSD上只测量了沿一个方向的变化:

(8)

得到:

(9)

其中,f是PSD上的焦距,在这个实验中是30 cm。σx是从PSD在大约30 s的积分时间内记录的图像运动数据计算出来的。然后,FWHM角θ的值由公式计算:

(10)

利用下述公式,将短曝光角像运动的方差与长曝光的弗里德参数r0联系起来:

(11)

测试以两种配置进行:1.在第一种配置中,镜子被简单地放置在实验室的地板上,处于“露天”状态,第二种配置包括用直径30 cm的八边形纸板圆顶和6 cm宽的狭缝包围镜子。

根据FWHM或图像大小评估结果,并假设湍流遵循科尔莫戈罗夫定律。从结果来说,由于镜面对流与内部圆顶表面的相互作用,圆顶结构显示出比露天结构更低的ΔTs。这表示视宁度数值的增加是由于镜子正上方的空气对流的某种影响,即镜面视宁度。

3.4 其他检测与视宁度

除了三种视宁度的检测方法之外,在其他相似领域的一些检测方法,对视宁度的检测也可起到一定的启发,如海洋湍流的检测,三维光学测量技术等,这些方法,对之后各类视宁度检测方法的创新,将有一定帮助。

3.4.1 海洋湍流与视宁度检测

近年来,基于激光的光学成像、传感和通信系统在沿海和深水应用中越来越广泛。与大气类似,海洋中也存在光学湍流,对海洋探测激光束传播造成影响。因此,需要对海洋中的光学湍流进行检测,而海洋湍流检测的构想,也可以应用于大气湍流的检测中去,对于各类视宁度检测也有所启发。

为了测量清澈海水中光学湍流对激光束传播的影响,并定量表征这些对光学通道的影响,研究了一种装置。这种装置在自然产生的湍流中,在一定距离的垂直路径上,向光束剖面仪投射密集的激光束。从光束偏转中提取折射率结构常数[21]。

(12)

2011年进行的巴哈马光学湍流检测(BOTEX)[22-23]利用测量装置研究了光学湍流对激光束在8.75 m路径长度的清澈海水中传播的影响。通过光学湍流区域传播的激光束遭受相位前沿的随机变化,导致光束形状的扭曲以及光束偏转。

图11展示了接收器和发射器的详细视图,图11(a)中的插入显示了摄像机从磨砂玻璃背面记录的投射光点,图11(c)是发射器和接收器设置的示意图。发射器向有源区域投射21×21光束网格,形成高速位置敏感光探测器或光束剖面仪。21×21光束由衍射光学元件形成;激光被扩展以填充整个DOE,然后通过一组透镜聚焦到光束轮廓仪上。大面积光束轮廓仪由一个CCD单色高速摄像机组成,该摄像机配备了一个8 mm的物镜,从磨砂玻璃片的背面记录强度图像。由于21×21光束网格的扩展(相邻光束之间的间距为0.17)和探测器的有限尺寸,只有大约20束单独的光束落在磨砂玻璃板上,并被摄像机记录下来。每个激光点由光束直径上大约10个电荷耦合器件像素分辨。

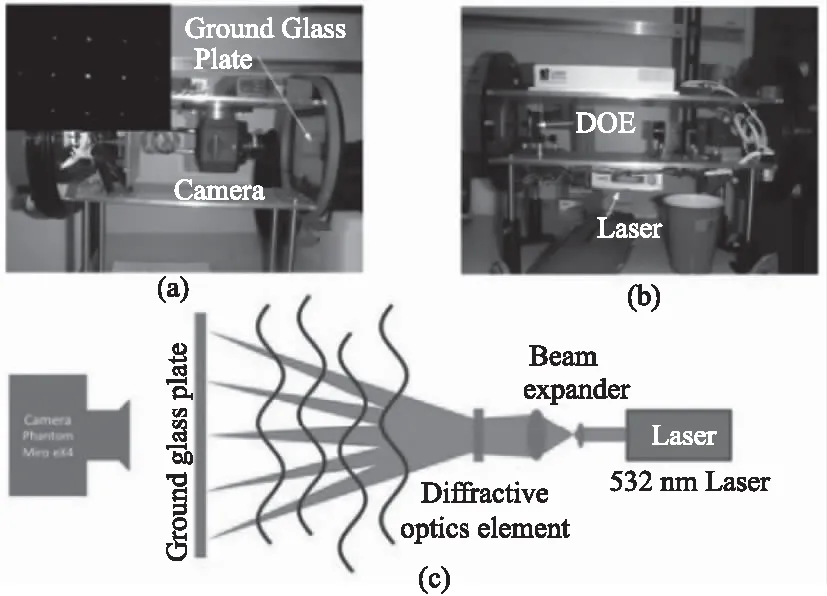
图11 接收器和发射器的详细视图[21]

3.4.2 条纹投影轮廓术(FPP)

在静态物体的图像重建领域,三维光学测量技术的应用十分广泛。在众多三维光学测量技术中,基于相位测量的条纹投影轮廓术(FPP)因其非接触、高空间分辨率、高测量精度和良好的系统灵活性而成为最有前途的三维成像方法之一。目在一些重要的应用中,在不断变化的动态场景中获取高质量的三维信息是必不可少的,而应用条纹投影轮廓术能够快速和精确地获取这些信息,进行三维重建。这项技术能够将条纹图像恢复为被测物体相位信息,甚至是三维重构。

条纹投影轮廓术(FPP)的原理如图12所示,投影仪将一系列条纹图案投射到目标物体上,然后相机捕捉这些被物体调制和变形的图像。利用捕获的条纹图,可以通过条纹分析算法提取被测物体的相位信息。

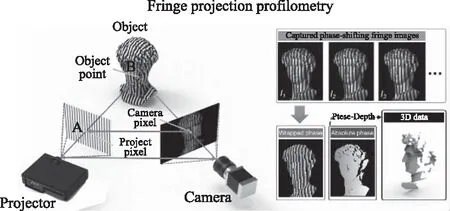
图12 条纹投影轮廓术的基本原理[24]

传统的多频合成方法无法保证单帧高精度三维成像,受深度学习在FPP成功应用的启发,南京理工大学陈钱、左超教授课题组提出了一种基于单次深度学习的双频合成条纹投影轮廓术[24],该方法可以在只有单幅条纹投影图像的前提下,实现无频谱混叠的高质量相位信息检索、鲁棒的相位模糊消除和高精度的动态三维面形测量。

基于深度学习的双频复用结构光条纹解调技术的发展,实现了真正意义上的单帧高精度无歧义三维重构,为复杂、高速运动物体的三维面型准确的测量开辟了新途径。基于这种方法,结合冻结湍流假设,在一定时间内把湍流看作是一个静态的物体,那么利用条纹投影轮廓术,就能快速对湍流信息进行测量,获取相位信息,然后进行三维重建,从而获得视宁度。

4 结论与展望

综上所述,经过几十年的发展,在大气视宁度探测方面,现有的方法与仪器,如SCRDAR[25-26]、DIMM[27]、MASS[28-30]等,都已经相当成熟。而在圆顶视宁度模拟检测方面,CFD的应用在该领域取得了重要的成果。随着日渐普及的自适应光学技术应用的需要,以及天文选址的迫切需求和重点发展,在该领域的研究也将进一步进行。

目前地基式天文望远镜对口径和分辨率的追求已经发展到一个新的阶段,望远镜自身引起的空气湍流对像质的影响变得更为突出。天文学家通过差分像运动法等方法测量望远镜光路上整个大气层的视宁度,通过闪烁仪等测量近地面的圆顶视宁度。而测量镜面附近空气的实时视宁度参数,则主要是通过测量波前斜率或到达角波动来计算镜面视宁度[31-34]。随着望远镜的口径不断增大,镜面视宁度的影响越发的不可忽视,因此,对于镜面视宁度检测方法的研究,将是未来几年到几十年内,在大口径望远镜建造方面,需要重点解决的问题。