基于小增益和Lipschitz条件的闭环EIV系统稳定性分析

王建宏,张金龙,罗熙

(江西理工大学电气工程与自动化学院,江西 赣州 341000)

系统是普遍存在、随处可见的,目前许多实际的系统都是在反馈控制的情况下运行。实际系统中,由于传感器故障、测量方法及周围环境的干扰等很多因素,测量误差十分普遍地存在于很多领域,例如经济、医疗、工业过程等[1]。对于输入和输出都受到外界噪声干扰的系统称为变量误差(EIV)系统,目前对EIV线性系统动态辨识的研究比较广泛。Söderström[2]对EIV系统做了调查,给出了EIV系统识别的背景、动机和识别的几种方法。Söderström等[3]提出了当测量噪声相互关联时,EIV的识别方法,并将广义工具变量估计器(GIVE)推广到输入噪声和输出噪声相互关联的白噪声变量误差模型中。 Kreiberg等[4]将结构方程模型(SEM)应用到EIV系统中,提出了如何将EIV单输入单输出(SISO)系统表示为SEM的2种方案。Söderströ等[5]讨论研究了当无噪声输入没有周期性为任意信号时EIV模型的识别问题,提出了最大似然方法。Kang等[6]使用图形子空间方法处理EIV系统参数的估计,提出了一种比常用的最小二乘法更为通用的估计算法。Zhang等[7]在变量误差框架内对线性动态系统的非参数识别。Khorasani等[8]研究了EIV系统参数的非渐近置信区域的构造问题,后面又研究了变量误差系统传递函数的非渐近置信区域[9]。Zhang等[10]研究了干扰为有色噪声、输入为准平稳的线性动态EIV的问题,提出了扩展的频域极大似然估计的新公式,它减少了非线性正态方程的解的数量要求。

目前许多研究大部分都是对EIV线性系统进行识别,而没有对其稳定性进行分析。本文在EIV系统的基础上加点改进,在其输出端加上负反馈,那么系统的输入和输出噪声干扰会影响到系统的稳定性。对于一个系统而言,稳定性是第一位,而李雅普诺夫函数是验证系统稳定性的一种常用方法。但是,该方法是一个充分条件,很难构造一个满足充分条件的李雅普诺夫函数。因此,针对闭环变量带误差系统使用以下2种方法。第1种是直接使用输入输出稳定的小增益定理,避免了构造李雅普诺夫函数的困难。第2种是使用Lipschitz条件推出系统是有界输入有界输出稳定的,这2种方法本质上相同。第2种是受到了关于非线性闭环系统结构的稳定性分析的启发,特别是使用Lipschitz对系统稳定性的推理[11]。

小增益定理超越了李雅普诺夫理论,在过去50年里对不确定系统的稳定性分析和综合控制发挥了重要作用,是现代控制理论历史上的一个里程碑[12]。Liu等[13]将小增益定理改进并应用到以外部干扰为输入的闭环事件触发系统的输入状态稳定性(ISS)分析。Bao等[14]将输入输出稳定的小增益定理应用到混合子系统所组成的大型互联系统中。Liu等[15]在事件触发控制的研究中利用了输入到状态稳定的小增益定理,将事件触发控制问题转化为输入状态稳定问题,并利用ISS的小增益参数来严格检验事件触发控制的前向完备性,提出了一种控制非线性不确定系统事件触发控制设计的新方法,解决了非线性基准测试系统的事件触发控制问题。Wu等[16]将输入到状态稳定的小增益定理应用到自适应反馈控制器的设计。将自适应神经设计、输入状态稳定分析和小增益定理相结合,解决了非仿射纯反馈系统控制的难题,避免了闭环系统整体李雅普诺夫函数的构造,从而克服了纯反馈系统神经网络控制中的循环设计问题[17]。

1 小增益定理的基本知识

在研究闭环变量带误差系统的稳定性分析之前,先了解有关小增益的一些基本知识[18],首先给出以下定义。

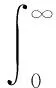
(1)

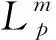
考虑从输入信号u∈Lm到输出信号y∈Lq的映射。由于按信号范数的定义,只有有界的或稳定的信号u∈Lm和信号y∈Lq才有定义。考虑处理不稳定的系统,因此对信号空间Lm和Lq进行扩充,把不稳定的信号扩充进去。

定义2u的截断函数定义为

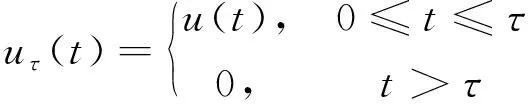
(2)

1.1 系统有限增益L稳定

‖(Hu)τ‖L≤γ‖uτ‖L+β

(3)

满足式(3)的最小增益γ被称为系统增益,系统有一小于或等于γ的L增益,有限增益L稳定性是一个输入输出意义上的稳定性。

因信号空间的不同,有限增益L稳定可分为L1、L2、Lp、L∞稳定,其中L∞稳定对每个有界输入u(t),其对应的输出Hu(t)是有界的,因此L∞稳定也被称为输入有界输出有界稳定,或称系统具有有界输入有界输出稳定性。

对定义4说明:

1)定义中β项为偏移项。包含β项是为了便于在u=0时Hu≠0的系统使用。

2)系统增益γ取值应尽可能小。

3)范数是在信号函数空间定义的,下标L不能省略,在全时间过程进行度量。

4)对于因果的且有限增益L稳定的系统,作如下推导:

则有

u∈Lm⟹Hu∈Lq

5)定义是以映射y=Hu是因果的为前提的。

1.2 反馈互联系统的小增益定理

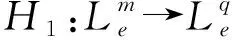
图1 反馈互联系统Fig.1 Feedback interconnection system

(4)

(5)

互联后,各信号可以向量表示为

反馈互联系统有限增益L稳定被定义为u→y有限增益L稳定,其向量表示为

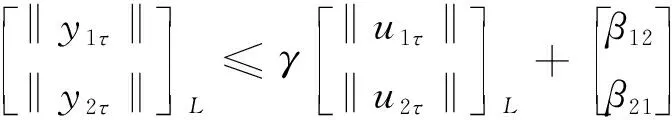
(6)

式中:γ为一正值常数矩阵。

‖y1τ‖L≤γ11‖u1τ‖L+γ12‖u2τ‖L+β12

(7)

‖y2τ‖L≤γ21‖u1τ‖L+γ22‖u2τ‖L+β21

(8)

易证明,u→e有限增益L稳定当且仅当u→y有限增益L稳定。因此当u→e、u→y中任何一个是有限增益L稳定时,反馈互联系统都是有限增益L稳定的。

参与互联的子系统H1和H2分别满足有限增益L稳定条件式(7)和式(8)并不一定能保证整个反馈互联系统有限增益L稳定。为了研究什么条件能够实现有限增益L稳定,引出了小增益定理。小增益定理如下:在前述系统假设下,如果反馈互联系统回路总增益γ1γ2<1,则反馈互联系统是有限增益稳定的。证明如下。

证明在图1的反馈互联系统中,假设e1、e2存在,由互联关系得

e1τ=u1τ-(H2e2)τ

(9)

e2τ=u2τ+(H1e1)τ

(10)

由于其子系统是有限增益L稳定的,满足式(4)、式(5),联合式(9)和式(5)可得:

‖e1τ‖L≤‖u1τ‖L+‖(H2e2)τ‖L≤‖u1τ‖L+

γ2‖e2τ‖L+β2≤‖u1τ‖L+γ2(‖u2τ‖L+

γ1‖e1τ‖L+β1)+β2=γ1γ2‖e1τ‖L+

(‖u1τ‖L+γ2‖u2τ‖L+β2+γ2β1)

(11)

因为γ1γ2<1,所以对所有的τ∈[0,∞)有

β2+γ2β1)

(12)

同理,联合式(10)和式(4)可以得到

β1+γ1β2)

(13)

证明完毕。

注:该方法是充分条件,具体见仿真分析。

2 闭环变量带误差系统稳定性分析

对于一个系统而言,稳定性处在第一位,而系统含有扰动是不可避免的,所以对含有扰动的系统进行稳定性分析至关重要。

2.1 闭环变量带误差系统结构

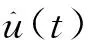
图2 闭环变量带误差系统结构Fig.2 Closed-loop variable with error system structure

根据图1反馈互联系统和图2闭环变量带误差系统结构,两图相比较,假设u(t)+d1(t)看作u1,d2(t)看作u2,那么闭环变量带误差系统的稳定性等同于反馈互联系统的稳定性。

2.2 线性时不变闭环变量带误差系统稳定性

从能量观点出发,使用L2稳定性对系统做稳定性分析,假设子系统是线性时不变系统,对于线性时不变系统

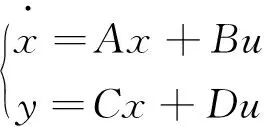
(14)

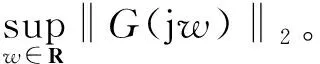
证明由于是线性系统,不失一般性,令x(0)=0,则y的Fourier变换是

(15)

输出y的L2范数

(16)

由Parseval定理得

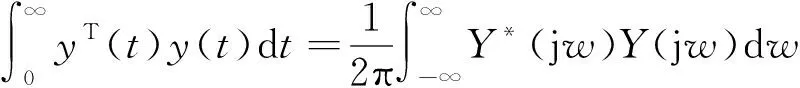
(17)

根据式(15)～式(17)可得输出y的L2范数平方为

(18)

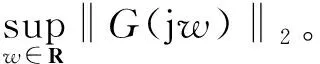
2.3 非线性闭环变量带误差系统稳定性分析

上面是对线性时不变的变量带误差系统求系统增益。接下来对于非线性的闭环变量带误差系统,同样可以求系统增益并利用小增益定理判断系统稳定性。但是除了直接用小增益定理之外,还有另外一种方法,即假如子系统是Lipschitz的,可以使用Lipschitz条件直接对整个系统的输入输出性质进行推导,从而确定系统的有限增益稳定性。本节主要使用Lipschitz条件确定系统的有界输入有界输出稳定性,其等同于系统的有限增益L∞稳定性。

以图1反馈互联系统为例,作如下假设条件:

1)子系统H1、H2满足Lipschitz条件,即系统是Lipschitz的。以子系统H1为例,必然∃γ∈[0,∞)和∀u1、u2满足

‖H1(u1)-H1(u2)‖∞≤γ‖u1-u2‖∞

式中:u1、u2为子系统H1的输入;γ为非负实数,也称Lipschitz常数,Lipschitz常数与使用的范数有关,如式(19)使用的是无穷范数。本节主要以无穷范数为例进行推导运算。

2)u1、u2有界,即‖u1‖∞≤εu,‖u2‖∞≤εy。

根据图1所示反馈互联系统的结构,得到

y1(t+1)=H1(e1(t))=H1(u1(t),y2(t))=

H1(u1(t),H2(e2(t)))=H1(y1(t),u1(t),u2(t))

(19)

为了方便,对式(19)符号变换,即

y(t+1)=f(y(t),u1(t),u2(t))

(20)

假设此时f(y(t),u1(t),u2(t))是满足上述假设条件1)和条件2),则有

‖f(y1(t),u1(t),u2(t))-f(y2(t),u1(t),u2(t))‖∞≤

γ‖y1(t)-y2(t)‖∞

(21)

(22)

(23)

‖u1(t)‖∞≤ε1,‖u2(t)‖∞≤ε2

(24)

此时

‖y(1)‖∞=‖f(y(0),u1(0),u2(0))‖∞=

‖f(y(0),u1(0),u2(0))-f(0,u1(0),u2(0))+

f(0,u1(0),u2(0))-f(0,0,u2(0))+

f(0,0,u2(0))-f(0,0,0)+f(0,0,0)‖∞≤

‖f(y(0),u1(0),u2(0))-f(0,u1(0),u2(0))‖∞+

‖f(0,u1(0),u2(0))-f(0,0,u2(0))‖∞+

‖f(0,0,u2(0))-f(0,0,0)‖∞+‖f(0,0,0)‖∞

(25)

联合式(21)～式(25)可得

‖y(1)‖∞≤γ‖y(0)‖∞+γu1‖u1(0)‖∞+

γu2‖u2(0)‖∞+‖f0‖∞≤

γ‖y(0)‖∞+γu1ε1+γu2ε2+‖f0‖∞

(26)

其中f0=f(0,0,0),同样地,经过一些计算,可以得到以下结果

‖y(2)‖∞≤γ‖y(1)‖∞+γu1‖u1(1)‖∞+

γu2‖u2(1)‖∞+‖f0‖∞≤

γ(γ‖y(0)‖∞+γu1ε1+γu2ε2+‖f0‖∞)+

γu1ε1+γu2ε2+‖f0‖∞≤

γ2‖y(0)‖∞+(γ+1)γu1ε1+

(γ+1)γu2ε2+(γ+1)‖f0‖∞

(27)

继续计算,最终得到

(28)

如果γ<1,则γt→0,式(28)可化简为

(29)

故该反馈互联系统是输入输出稳定的。该方法与反馈互联系统的小增益定理进行比较,相当于有限增益L∞稳定,下面将2种方法进行比较。

对于小增益定理,将反馈互联系统按输出形式展开,根据式(7)～式(10)得到

‖y1τ‖L∞≤γ1‖e1τ‖L∞+β1=

γ1(‖u1τ-y2τ‖L∞)+β1≤

γ1(‖u1τ‖L+‖y2τ‖L∞)+β1≤

γ1(‖u1τ‖L+γ2‖e2τ‖L∞+β2)+β1≤

γ1(‖u1τ‖L∞+γ2‖u2τ+y1τ‖L∞+β2)+β1≤

γ1‖u1τ‖L∞+γ1γ2‖u2τ‖L∞+γ1γ2‖y1τ‖L∞+

γ1β2+β1

(30)

将式(30)进一步化简得到

(31)

故系统的输出y1对有界输入u1和u2是输出有界的。这意味着可以从能量角度(2范数)和输入有界输出有界(无穷范数)的角度判断闭环变量带误差系统的稳定性,当然也可以其他范数形式判断稳定性。除了可以直接使用小增益定理证明稳定性外,还可以使用Lipschitz条件直接进行推导来实现稳定性判断。

接下来本文给出两者的联系。通过将式(29)和式(31)相比较可以发现

(32)

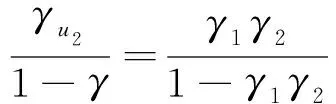
(33)

(34)

联合式(32)～式(34)可以轻易得到

γ=γ1γ2

(35)

γu1=γ1

(36)

γu2=γ1γ2

(37)

‖f0‖∞=γ1β2+β1

(38)

因此这2种分析方法本质相同,相互联系,当一种方法不好分析系统稳定性时,可以用另外一种。

3 仿真算例

在本节中,为了验证所提出的闭环变量带误差系统稳定性分析的可行性和有效性,本文分别对线性闭环变量带误差系统和非线性闭环变量带误差系统展开数值仿真并对仿真结果进行分析讨论。

3.1 线性闭环变量带误差系统仿真

下面进行数值仿真验证,对于图2结构形式的线性闭环变量带误差系统,将其看作反馈互联系统,则u(t)+d1(t)看作u1,d2(t)看作u2,闭环变量带误差系统的输出看作y1。假设输入u(t)=10,干扰是白噪声并将其放大10倍,并且d1(t)=d2(t),其中

G(s)=

(39)

(40)

将式(39)和式(40)转化为如式(14)形式的状态方程,可以得到子系统的系统矩阵AG和AC都是Hurwitz的。将扰动看作反馈互联系统的输入,可直接使用小增益定理判断系统稳定性。

以子系统C(s)为例,令s=jw

则

(41)

根据式(41)可求得

(42)

其中:H表示共轭转置。同样地,‖G(jw)‖2也是如此。‖G(jw)‖2和‖C(jw)‖2的图形如图3所示,则其增益为

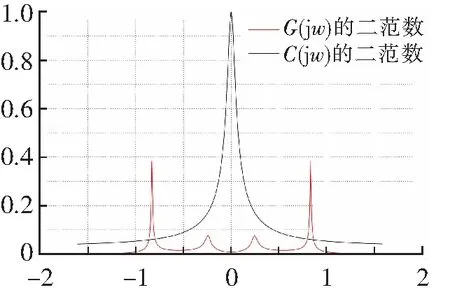
w图3 系统传递函数频域二范数Fig.3 System transfer function frequency domain two norm

故γ1γ2<1,整个闭环变量带误差系统是有限增益L2稳定的。系统扰动误差与系统输出仿真结果如图4所示,可以看出输出有界。如图5所示,将系统扰动误差与系统输出放在一起比较,发现系统可以在很大扰动下保持输出有界稳定。

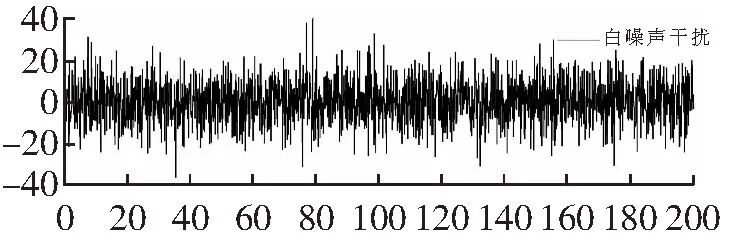
t/s

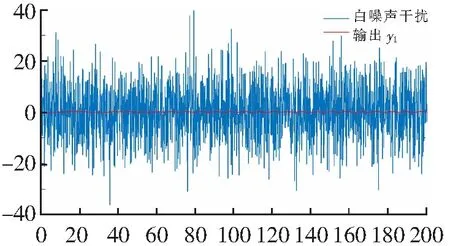
t/s图5 系统扰动和输出曲线对比图Fig.5 System disturbance and output curve comparison diagram

为了验证小增益定理对闭环变量带误差系统的稳定性分析是充分条件,可以保持其子系统G(s)不变,将子系统C(s)变为

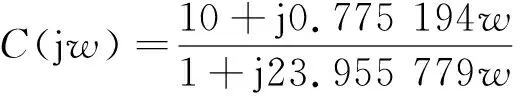
则可取

由于G(s)不变,可以得到

故γ1γ2>3,不满足小增益定理。此时系统扰动和输出曲线如图6所示,系统扰动和输出曲线对比如图7所示,整个系统仍然是有界输入有输出稳定的,故小增益定理是充分条件。

t/s

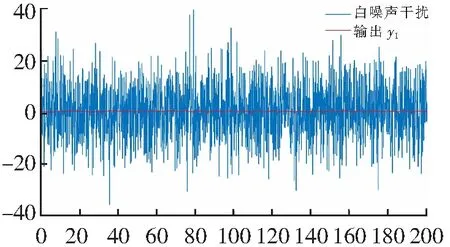
t/s图7 γ1γ2>1时系统扰动和输出曲线对比图Fig.7 When γ1γ2>1 system disturbance and output curve comparison diagram

3.2 非线性闭环变量带误差系统仿真

对于非线性闭环变量带误差系统,其子系统是非线性的,不能写成传递函数的形式,接下来本文使用L∞增益的小增益定理来对系统的稳定性进行分析,并对结果进行讨论验证。

将非线性闭环变量带误差系统看作反馈互联系统,同理3.1小节。此时u(t)+d1(t)看作u1,d2(t)看作u2,非线性闭环变量带误差系统的输出看作y1。假设输入u(t)=1,干扰d1(t)=d2(t)且是白噪声的0.1倍,则有

(43)

‖u1‖L∞=‖u(t)+d1(t)‖L∞=1.4

(44)

‖u2‖L∞=‖d2(t)‖L∞=0.4

(45)

假设子系统H1的输入输出关系为

(46)

子系统H2的输入输出关系为

y2=h2(u)=ud

(47)

其中a、b、c、d是非负常数。

下面推导输出和输入之间的不等式关系,对于子系统H1,对双曲正切函数求导,得

(48)

当u=0时,函数斜率有最大值,故有

|tanh(cu)|≤|tanh'(cu)|max×|u|≤

(49)

根据式(46)和式(49)得

‖y1‖L∞=‖au+btanh(cu)‖L∞≤

(a+bc)‖u‖L∞

(50)

根据式(3)或式(4)可知H1的系统增益为

γ1=a+bc

(51)

同理,对于式(47),对于子系统H2可以得到

‖y2‖L∞≤d‖u‖L∞

(52)

其系统增益为

γ2=d

(53)

如果使用Lipschitz的分析方法,会发现2个子系统的Lipschitz常数就是γ1=a+bc和γ2=d。

在对参数a、b、c、d赋值之前,先作如下分析,根据式(31),将不等式的右端设为f(γ1,γ2),则

(54)

根据式(50)和式(52)得

β1=0,β2=0

(55)

令‖u1τ‖L∞=M1>0,‖u2τ‖L∞=M2>0可得

(56)

其中M1和M2是常数,γ1>0,γ2>0,γ1γ2<1。

将式(56)中f(γ1,γ2)对γ1求偏导数得

(57)

对γ2求偏导数得

(58)

根据式(31)、式(57)、式(58),f(γ1,γ2)随γ1和γ2的增大而增大。当γ1和γ2的值变小,f(γ1,γ2)会变小,从而整个反馈互联系统的输出上界会变小。因此γ1和γ2的值越小越好,但是对于系统实际的输出上界并不是这么简单的规律,具体分析如下。

在非线性闭环变量带误差系统中,子系统如式(46)和式(47),对参数a、b、c、d取不同的值,可以得到不同的系统增益γ1和γ2。则在子系统构成的非线性闭环变量带误差系统中,令γ1和γ2取0.5或0.2,对于不同的γ1和γ2值输出y1的曲线如图8～图11。

t/s图8 γ1=0.5,γ2=0.5系统输出曲线图Fig.8 γ1=0.5,γ2=0.5 system output curve diagram

其中γ1取0.5,有

a=0.2,b=0.3,c=1

γ1取0.2,有

a=0.1,b=0.1,c=1

对于γ2取0.2或0.5,有γ2=d=0.2或γ2=d=0.5。图8中:

γ1=0.5,γ2=0.5,γ1γ2=0.25

(59)

根据式(44)、式(45)、式(54)、式(55)、式(59)得

0.4≈1.066 7

(60)

同理,图9中:

t/s图9 γ1=0.5,γ2=0.2系统输出曲线图Fig.9 γ1=0.5,γ2=0.2 system output curve diagram

γ1=0.5,γ2=0.2,γ1γ2=0.1

(61)

0.4≈0.822

(62)

同理,图10中:

t/s图10 γ1=0.2,γ2=0.5系统输出曲线图Fig.10 γ1=0.2,γ2=0.5 system output curve diagram

γ1=0.2,γ2=0.5,γ1γ2=0.1

(63)

0.4≈0.355 6

(64)

同理,图11中:

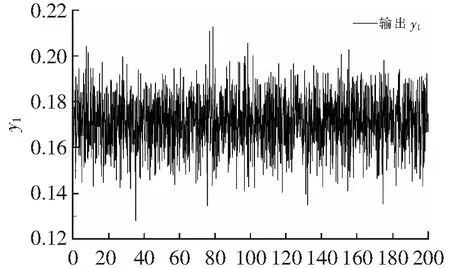
t/s图11 γ1=0.2,γ2=0.2系统输出曲线图Fig.11 γ1=0.2,γ2=0.2 system output curve diagram

γ1=0.2,γ2=0.2,γ1γ2=0.04

(65)

0.4≈0.308 3

(66)

根据式(60)、式(62)、式(64)、式(66)得

f(0.2,0.2)

f(0.2,0.2)

由此可以得出有限增益γ值越小,根据式(31)中小增益定理得出的输出的上界f(γ1,γ2)越小。

如图8～图11所示,图中曲线是系统的实际输出,可以得到不同的‖y1‖L∞值,该值是实际输出的最小上界且满足式(31),证明了小增益定理的有效性和可行性。

将图8和图9对比,图10和图11对比可以得到当γ1不变,γ2越小时实际输出的最小上界变大,但这并没有违反小增益定理中γ越小越好的结论,因为小增益定理中是上界而非最小上界。对比图8和图11可以发现当γ1和γ2一起变小,此时实际输出的最小上界同样变小。

对于γ1不变,γ2变小而最小上界变大的情况进行如下讨论,根据式(30)得

‖y1τ‖L∞≤γ1‖e1τ‖L∞+β1=

γ1(‖u1τ-y2τ‖L∞)+β1

(67)

将数据代入,则u1>0。当γ2变小时y2会缩小,造成上述情况的原因是γ2变小时‖u1τ-y2τ‖L∞变大,设γ1=0.5,γ2从0.5变到0.2时e1=u1-y2的曲线如图12所示,增益变小后上界变大。

t/s

4 结束语

本文研究了闭环变量带误差系统的输入输出意义上的稳定性分析。在分析之前,将系统视为黑盒子,只过问输入、输出,不过问系统内部状态,并给出了输入输出意义上的稳定性概念L稳定性和反馈互联系统的小增益定理。对于含有输入输出扰动误差的闭环系统,将其看作是一个反馈互联系统,可以直接应用小增益定理对闭环变量带误差系统进行稳定性分析。除此之外,还可以使用Lipschitiz常数并利用几何级数的收敛性进行稳定性分析。另外,针对这2种稳定性分析方法给出了其中的联系。最后,使用数值分析证明了该方法的有效性和可行性,并对仿真结果进行讨论。同样地,该稳定性分析方法可以扩展到其他闭环控制系统中,比如模型预测控制和自适应控制等。