基于LS-DYNA动力电池包底部球击失效分析

程生,吕希祥,韦助荣

(合肥国轩高科动力能源有限公司,安徽 合肥 230011)

近年来,随着新能源汽车的迅猛发展与广泛应用,其动力电池包的安全保障,常常成为汽车安全的热议话题,也是制约着新能源汽车整体安全水平、技术能力的提高、成本精准控制和推广应用的核心问题。在行车过程中,动力电池包的底部受到剐蹭、挤压时,会产生较大冲击力。相关研究表明,底部受到向上撞击事故占比较多,占车底部碰撞总事故率约46%[1]。下箱体底部需要良好的刚度和强度保障锂电池模组不受到挤压,避免短路、电芯内部锂晶体穿刺等化学反应,导致热管理性能与续航能力的下降[2-3]。

目前,文献[4-8]将GISSMO(generalized incremental stress dependent damage model)理论引入数值模拟中,作为材料失效本构模型,文献[9]针对汽车用6016铝合金板材为研究对象,设计6种可呈现不同应力三轴度水平的样件模型,利用LS-DYNA软件将GISSMO失效本构模型用于汽车发动机罩内板在冲压过程的断裂失效问题,数值模拟与试验结果的高度吻合性,产品均未出现裂纹区域,表明GISSMO失效模型适用于准确预测6016铝合金板材的断裂行为;文献[10]采用物理试验和仿真对标的方法,开发了基于GISSMO材料失效的螺栓分析模型,仿真中的断裂力值、断裂时间和失效模式的一致性,表明其在整车仿真分析中具有较高实用性;文献[11]从连续介质损伤理论出发,进行高强度热冲压淬火后材料损伤行为的研究,将损伤因素引入到典型车身薄壁结构的抗撞性能分析当中,可有效预测实际热成形车身结构碰撞变形行为。

因此,本文基于LS-DYNA显动力学分析软件,将GISSMO理论引入到动力电池包底部球击分析中,预测材料失效行为。

1 电池包结构与材料失效分析方法

1.1 电池包箱体结构介绍

目前乘用车常用的电池包多为铝合金型材件进行拼焊而成,如图1所示,模组直接通过螺栓安装于箱体上,与上底板之间垫有可起缓冲作用的泡棉。当电池包底部受到侵入破坏时,上底板的突起变形会直接侵入模组底部,带来安全风险。故底板采用双层底板的设计方案,底板分上底板和下底板2层,可起到双层保护。

图1 某款动力电池包铝合金箱体结构Fig.1 Structure of a power battery pack aluminum alloy box

该款电池包箱体底板材料参数如下:材料型号为AL6005 T6,弹性模量为67 GPa,泊松比为0.33,屈服强度为240 MPa,抗拉强度为278 MPa,材料断裂延伸率为0.09,密度为7.8×10-6kg·mm-3。

1.2 GISSMO损伤失效模型

准确预测下底板的破坏,对整包安全性能的评估有着十分重要的作用。借助于先进的仿真技术手段,是最为可行的方法。较为常用的仿真失效本构模型包括Johnson-Cook 断裂准则、成形极限图、CrachFEM模型以及GISSMO模型[12-14]。本文采用可考虑材料在不同受力状态下不同失效应变值、非线性应变路径成形及非线性损伤积累方式的GISSMO模型,作为失效本构模型。

GISSMO连续介质材料失效本构模型基于J-C模型发展而来[8],综合考虑材料在不同应力三轴度下累积损伤。应力三轴度定义为静水压力与Mises等效应力的比值,表征材料塑性变形能力的约束程度,同时也是影响材料失效时微孔洞演变规律的重要指标。应力三轴度计算公式如下:

损伤准则采用路径相关断裂准则,则损伤累积增量ΔD为

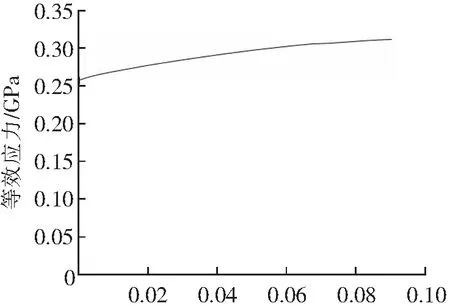
式中:ID为非线性损伤累积指数DMGEXP;εf为等效塑性应变失效值;D为损伤值(0

2 标准样件力学性能实验

力学性能试验通过实验机获得板材力学性能参数,样件为AL6005 T6铝合金板材,板料厚度为1.5 mm,如图2所示。室温环境下,通过准静态拉伸试验获得材料拉伸力-位移关系曲线,处理得到应力-应变关系曲线,如图3所示。

图2 铝合金板材样件Fig.2 Aluminum alloy sheet sample

塑性应变图3 等效应力-塑性应变关系曲线Fig.3 Relationship curve of equivalent stress and plastic strain

仿真拉伸力与位移关系变化趋势与实验结果数据吻合度较高,如图4所示,最大误差值低于0.6 mm,通过进行误差分析,均方差值为0.079,如图5所示,该计算模型满足失效分析计算精度要求。

(a) 单轴拉伸实验

(b) 模拟仿真结果(标准尺寸1.8 mm)图4 单轴拉伸实验与模拟仿真结果变形情况Fig.4 Deformation of uniaxial tensile experiments and simulation results

位移/mm图5 单向拉伸实验仿真与实验的误差分析Fig.5 Error analysis of unidirectional tensile experiment and simulation

3 CAE仿真分析

3.1 无失效本构模型分析结果

分析模型暂未设置材料失效本构,观察箱体底板塑性应变与等效应力分布情况。箱体底部塑性应变云图如图6所示,最大塑性应变主要位于刚性球与箱体底部接触区域,已超过材料断裂极限。箱体应力三轴度云图如图7所示,接触区域应力三轴度数值超过0.5,最大达到0.667。观察图8,位移达到9 mm时,破裂点塑性应变值超过材料断裂延伸率0.09,材料模型的累积损伤开始计算。观察图8发现,达到12.4 mm时,完全产生裂纹(仿真即网格单元的删除)。

图6 箱体塑性应变云图及局部放大图Fig.6 Plastic strain cloud and local enlarged diagram of box

图7 箱体应力三轴度云图Fig.7 Stress triaxiality cloud diagram of box

位移/mm图8 破裂点塑性应变值与位移关系曲线图Fig.8 Relationship between plastic strain value and displacement at rupture point

3.2 考虑失效本构模型分析结果

通过LS-DYNA软件仿真对标(图9),获得不同应力三轴度所对应的失效应变值。并绘制在二维图上,用光滑曲线拟合得到失效曲线,如图10所示。

位移/mm(a) 剪切实验拉伸曲线与变形情况对比 位移/mm(b) 拉伸实验拉伸曲线与变形情况对比

应力三轴度图10 应力三轴度与失效塑性应变关系曲线Fig.10 Curve of relationship between stress triaxiality and failure plastic strain

基于AL6005 T6铝合金板材对标分析所得GISSMO失效本构模型,对底板材料设置失效参数,失效模拟仿真过程即裂纹的演化过程,如图11所示,起始时下层底板底部与刚性球接触区域出现短小的一字型裂口,随着裂纹不断的向两端拓展,裂纹的长度不断增加,最后形成一段长长的裂缝。上层底板无明显裂缝,略有微微凸起。

图11 底板失效仿真过程Fig.11 Simulation process of bottom plate failure

4 试验验证与对比分析

4.1 试验验证

如图12所示,将电池包安装于工装上,标记球击球击位置点,安排底部球击实验。挤压刚性球直径150 mm,挤压速度为1 mm·s-1,待挤压力达到18 kN时,停止测试,记录停止时的挤压力和位移。电池包箱体底面变形与内部变形情况如图13所示,球击位置处,下层底板有破裂,上层底板黏结的保温棉未有明显变形痕迹。

图12 底部球击实验工装安装Fig.12 Tooling installation of bottom ball hit experiment

(a) 电池包箱体底面 (b) 电池包箱体内部

4.2 对比分析

如图14所示,通过底板失效位置对比发现,材料失效裂缝均呈一字型形式,仿真预测与实验的结果一致。从图15实验曲线观察可知,位移为15.1 mm左右,力位移曲线出现较大幅度陡降,此时底板开始撕裂,裂缝开始形成,这与图8仿真结果中材料破裂起始点结果较为接近。模组电芯无明显挤压迹象。模拟仿真曲线表明,同样出现一字型裂缝,位移为12.4 mm左右,力位移曲线亦出现陡降,各项数据对比分析如表1所示,整体误差较低,准确度满足设计要求。

图14 底板失效位置对比Fig.14 Comparison of the failure positions of the bottom plate

位移/mm图15 挤压力与位移关系曲线Fig.15 Relationship curve between the extrusion force and displacement

表1 实验与模拟仿真数据对比Tab.1 The comparison of experimental and simulation data

5 结论

通过本文所述试验和仿真模拟结果分析可得到如下结论:

1)通过采用LS-DYNA软件里GISSMO材料失效本构模型,针对6005 T6铝合金进行失效分析。单项拉伸实验的断裂形式可以得到较为准确的模拟,满足模型计算结果的一致性及准确性。

2)观察到力位移曲线,关于材料开始撕裂的时间点的预测,仿真模拟结果(12.4 mm)与实验结果(15.1 mm)的误差低于17.9%,已经满足工程应用的需求。故采用GISSMO失效本构模型,可以较为准确地判断材料破裂时间点。

3)通过底部球击实验结果及仿真模拟分析,材料失效裂缝均呈一字型形式,吻合度较高,裂缝长度的预测,误差为9.1%,表明采用GISSMO失效本构模型,可以较为准确地模拟实际裂纹的细节特征。