基于深度强化学习的微电网内多侧储能协同调度方法

谢 旭，张 哲，喻 乐，刘秉祺，李彦宾，陈 曦，张庭祥

（1.国家电网有限公司华北分部，北京 100083；2.北京清大科越股份有限公司，北京 100102；3.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

近年来，由可再生能源组成的混合发电系统发展迅速，广泛应用于分时定价（Time of Use，TOU）下的工业用户[1]。可再生能源发电的间歇性和不可预测性会导致电力系统的运行安全问题[2]，需要更好地了解可再生能源渗透率下所需的运行储备[3]。储能系统（Energy Storage System，ESS）通过转移负荷及平滑需求，可以促进可再生能源更好的并网，也可以改善供电质量、降低电力成本[4]。容量较高的存储系统可以提供更多的服务支持，如参与平衡、辅助服务等，同时需要为ESS部署各种控制器，如开/闭环、多智能体系统、优化方法等多侧储能方法[5]。

许多地区采用动态TOU形式，能源供应商通过TOU降低高峰期的需求[6]。通常TOU价格每年变化不超过两次，可能有2～3个价格水平，例如非高峰期、中高峰期和高峰期。ESS将在实行动态价格的住宅区发挥重要作用，在低价期储存能源，在高价期使用储存的能源，降低消费者的费用。

近年来，ESS的调度问题引起了研究人员的关注[7]。C D Korkas[8]提出了基于动态规划的ESS运行优化方法，在不牺牲用户偏好和满意度的情况下，获取最低的能源成本。G Zhang[9]利用随机非凸优化最小化并网微电网的总体运行成本，将非凸随机优化问题转化为凸优化问题进行求解。文献[10]提出了一种随机动态规划，利用现有的预测量优化储能系统的运行。文献[11]为储能业主制定了一个随机优化问题，在市场价格不确定的情况下实现套利利润最大化。这两项研究均需要预测电价，然而，很难在实时市场中得到准确的预测值[12]。

本文基于Q学习方法开发出一种易于实现的套利政策，以增强储能系统的价值积累。在没有明确假设分布的情况下，所提出的方法能够在不断变化的价格下运行。随着时间的推移，通过在不同的实时价格下反复执行充电和放电行为，达到累积奖励最大化。本文所提出的方法是不需要任何系统模型信息的无模型方法，对于TOU调度和节点边际电价（LMP）能源套利的组合，遵循通过Q学习获得的政策，极大地降低了多种能源成本。

1 储能系统调度模型

电力系统的边际成本往往随着需求的增加而增加，例如高峰时的电力需求决定了输电总容量，因此扁平化的电力需求被认为是降低电力公司成本的重要因素之一。具有反映需求变化动态价格的费率结构，如实时定价（Real Time Pricing，RTP）、日前定价（Day Ahead Pricing，DAP）和TOU模式，可以通过消费者对价格变化的反应来帮助平抑高峰需求，降低电力生产成本。

本文从用户角度解决实时储能系统充电/放电调度问题。假设储能系统的额定功率为5 kW，额定电池容量为14 kW·h，并假设储能没有退化，调度效率为100%，充电状态（State-of-Charge，SOC）限制为额定电池容量的10%和90%。一个具有离散时间步长的有限Markov决策过程可用于描述这个问题。假设两个相邻步之间的时间间隔为0.25 h，在时间步骤t，观察系统状态s（t），其中包括剩余能量和过去24 h的电价信息。基于这些信息，将选择充电/放电的动作a（t）。a（t）代表了储能系统在这个时间间隔内将被充电或放电。在执行这个动作后，可以观察到新的系统状态s（t+1），并为时间步骤t+1选择新的充电/放电动作a（t+1）。为防止同时进行充电和放电，或从多个来源进行充电/放电，在t时刻储能装置的充放电策略定义如下：

式中：cm（t）为t时刻来自LMP的充电功率，当a（t）=cm（t）时，表示以当前LMP价格购买能量为ESS充电；cu（t）为t时刻来自TOU的充电功率，当a（t）=cu（t）时，表示以TOU价格充电；du（t）为t时刻来自TOU的放电功率，当a（t）=du（t）时，表示以TOU价格放电；dm（t）为t时刻来自LMP的放电功率，当a（t）=dm（t）时，表示以当前LMP价格出售从ESS放出的能量；当a（t）=0（t）时，表示ESS既不充电也不放电。

从年初到时间t的累计收入V可以定义为

式中：h为数据的周期，本文中h=0.25 h；m（Δt），为Δt时刻LMP；u（Δt）为Δt时刻TOU；l（Δt）为Δt时刻负荷。

对于基于TOU的调度策略，ESS仅在最低电价时以全额额定功率充电，而在最高电价时放电。如果最低电价的时间段形成了Tlow集，最高电价的时间段形成了Thigh集，则累计收入表达式如下：

式中：Cmax为最大充电功率；Dmax为最大放电功率。

对于基于LMP的调度策略，假设p（t）为t时刻的LMP，s（t）=dm（t）-cm（t），则累计收入为如下优化问题的解：

式中：Emin为最低限度的SOC；Emax为最大限度的SOC；E（t）为t时刻储能的SOC；r（t-1）为前一时刻的回报值。

2 基于深度强化学习的储能协同调度方法

2.1 基于强化学习的调度方法

Markov决策过程是一个五元组[S，A，P.（·，·），R.（·，·），γ]，其中，S为系统状态，A为一个有限的行动集合，P.（·，·）为状态转换概率，R.（·，·）为奖励，γ为衰减率。考虑到能源的TOU成本、LMP价格、ESS的SOC状态和负荷情况，采用Q学习的方法优化ESS调度行为。

首先，将系统在t时刻的状态定义为向量s（t）=[du（t），E（t），cu（t），l（t）]，这包括了4个部分：TOU，SOC，LMP和负荷。给定状态s（t），a（t）定义为a（t）=[cm（t），dm（t），0（t），cu（t），du（t）]。在每个动作中，ESS试图以最大的允许速率进行充电或放电。在ESS没有过度/不足充电风险的情况下，即充电/放电不会导致E（t）超过Emax或低于Emin，那么调度将以全额定功率5 kW进行。

t时刻，在状态s（t）∈δ下采取动作a（t）∈A后，为了评价动作的好坏，储能器将收到一个奖励。储能的目的是通过在低价位充电和在高价位放电实现套利利润最大化。因此，可以将这种奖励定义为

式中：m（t）为LMP的移动平均值；上标a1，a2，a4，a5表示动作只保留当前项，令其他项为0，这确保了奖励来自于所定义的动作域。

式中：η为一种用于决定奖励重要性的参数。

在给定系统状态s（t）条件下，充电/放电调度质量由K个时间步长的未来奖励的预期总和来评价，如下所示：

式中：Qπ（s，a）为动作值函数；π为充/放电政策，表示从系统状态到一种充/放电调度的映射；E（·）为计算期望值；γ为衰减率，0＜γ＜1，用以平衡当前奖励和未来奖励之间的重要性。

调度问题的目标在于寻找一个最优的政策π*，使得动作值函数达到最大，即：

2.2 深度网络近似的最优动作值函数

由于未来的电价和用户行为都是未知的，所以很难以解析的方式确定出最优政策π*。强化学习（RL）的解决方案是根据Bellman方程迭代式地更新Qπ（s，a）。

随着迭代次数i→∞，Q（s，a）将收敛到最优动作值函数Q*（s，a）。通过一个贪婪策略确定最优调度：

Q*（s，a）通常由一个检索表来近似。在本文的问题中，电价是连续且高维的，需要一个极其庞大的表来近似Q*（s，a），而更新这样一个表是难以做到的。为此，本文利用一个深度卷积神经网络来近似Q*（s，a），更新公式可以表示为

式中：α为学习率；w为网络权重。

在均方误差条件下，利用梯度下降法更新网络参数，可使得动作值函数达到最优。

3 案例分析

发电侧储能模式需要利用负荷数据、TOU数据，而电网侧储能模式涉及到LMP数据。负荷数据采集于Pecan Street Dataport数据库，从中获取一处建筑从2014-07-08T00：00-2015-06-30T23：45的数据，采样周期为15 min，负荷功率和光伏发电功率分别如图1（a），（b）所示，TOU数据采集自电力公司，如图1（c）所示。LMP数据采集于COVID-EMDA数据库[13]，选择了该时间段内San Diego URBAN-N005节点的数据，如图1（d）所示。

图1 测试数据中微电网出力情况Fig.1 Microgrid power output in test data

为验证本文所提出的方法的有效性，在上述场景下，将所提出的方法分别与TOU策略方法、优化的TOU策略方法[14]及LMP策略方法[15]进行对比。对于TOU策略，储能系统仅在最低电价时以全额额定功率充电，而在最高电价时放电。对于优化的TOU策略，储能系统以减少峰值电费和最小化直流电费总额为目标，同时考虑了电池漏电、转换损失等约束。LMP策略是将现货市场中的储能系统建模为马尔可夫决策过程，并推导出一个Q-学习策略来控制储能的充电/放电。模型中的衰减率γ=0.99，学习率α=0.000 1，训练时的批次大小为32，随机初始化网络权重w，隐层和输出层的单元数量分别为64和10，迭代次数设置为1 000。

图2显示了根据本文所提出的方法及其他方法所产生的累计运行成本。从图中可以看出，由Q-学习策略所导致的动作比TOU策略下的总能源成本有着较大程度上的降低。实际上，Q-学习策略在大多数情况下选择用TOU的方式释放储能，抵消了负载的分时能源成本，而在少数情况下以LMP的方式出售能源，如图3所示。由于本文所提出的方法综合考虑了TOU和LMP，能够从这两部分成本中选取较便宜的部分，所以进一步降低了能源成本。

图2 不同方法在测试数据上的累积运行成本Fig.2 Cumulative operating costs of different scheduling strategies on test data

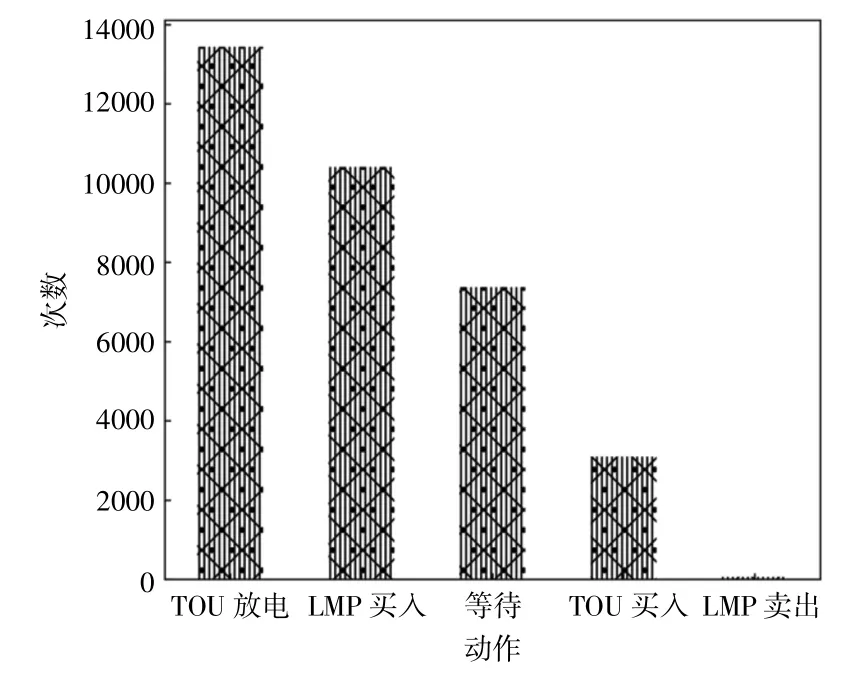
图3 本文所提出的方法中Q-学习行动策略全年的分配Fig.3 Distribution of Q-learning action strategies throughout the year in the proposed method

为了进一步研究本文所提方法的性能，图4展示了负荷较高的2 d内储能系统调度。可以看到，在第1天06：00-18：00，储能系统的能量主要来自于PV发电，所以储能系统的充电模式处于0值附近，在夜间受分时电价、节点边际电价、光照等因素的影响，储能系统的能量存储主要来源于放电模式。在第2天，由于电价的调整，06：00-18：00储能系统的能量来自于PV发电和放电模式。因此，本文所提出的方法能够在TOU和节点边际电价较低时进行充电，在分时电价和节点边际电价高峰期时进行放电。这些充电/放电模式验证了本文所提出的方法具有降低能源成本的能力。

图4测试数据中负荷较高的2 d内储能系统调度结果Fig.4 Results of energy storage system dispatch during the 2 days of higher load in the test data

4 结论

本文从用户的角度出发，将储能系统调度问题表述为一个具有未知过渡概率的Markov决策过程。考虑了TOU调度和LMP能源套利，提出了一种基于深度强化学习的方法来确定实时调度问题的最优策略。所提出的方法是一种无模型的方法，不需要任何系统模型信息。在提出的方法中，对于TOU调度和LMP能源套利的组合，遵循通过Q学习获得的政策，利用不同成本的多种能源，使得能源成本极大地降低。对比结果表明，所提出的方法优于基准解决方案。此外，所提出的方法可以满足不同用户对节约成本目标和减少范围焦虑目标的偏好。