结构参数约束下的磁场补偿式双层时栅角位移传感器研究

杨继森 周 润 张天恒 卢 渝 吴 灼 张 迪 张 静

重庆理工大学机械检测技术与装备教育部工程研究中心,重庆,400054

0 引言

近年来,我国制造业正迅速向高质量制造转型升级,高质量制造对位移传感器的测量精度提出了更高要求,研究高精度位移传感器显得愈发重要与紧迫[1-5]。时栅位移传感器作为一种新型位移传感器,以匀速运动的场为参考系,将空间位置测量转化为相对时间测量,提供了一种新型位移传感思路,提高了传感器测量精度。传感器以抗干扰能力强、精度高、抗油污、抗抖动等特点广泛用于数控机床、工业机器人以及军用领域等[6-8]。

场作为时栅位移传感器测量过程中的重要部分,场的匀速性与均匀性直接影响了传感测量精度,在研究进程中一直作为重点研究对象。如今印刷电路板(printed circuit board,PCB)工艺成熟,布线精度高,灵活度强,制造周期短,有助于优化传感器布线结构,增强场的匀速性,提高传感器的测量精度[9-11]。时栅位移传感器也从以前“开槽绕线式”结构转变为由PCB工艺制造的平面线圈阵列结构。文献[12]中提出了反向串联“回”字形阵列结构,对传感器结构上进行了一定的优化,消除了齿槽效应,提高了行波磁场的运动匀速性,减小了测量结果的四次谐波误差;文献[13]在文献[12]的结构基础上采用非线性规划遗传算法对其结构参数进行优化,使得感应信号谐波畸变率减小了90%,测量精度得到了提高;文献[14]通过分析测量模型得到感应信号与平板间隔无关的规律,通过一系列结构变换将双排差动平板结构优化为单排差动平板结构,消除串扰与安装所带来的影响,提高传感器的信号稳定性、抗干扰能力,在200 mm的测量范围内测量误差值从300 nm减小至150 nm。笔者所在课题组在优化时栅位移传感器工作中,通过分析磁场式时栅的时变磁场产生原理,提出采用双层互补式线圈的时栅传感器设计方案,有效抑制了时变磁场“端部效应”,提高了测量精度[15]。后续的研究中发现,仿真过程均在理想的情况下进行,忽略了上下层线圈间距,进一步研究发现,线圈间距会引起上下层线圈在感应线圈平面产生的磁场不对称,使得理论上均匀对称的磁场在感应平面内分布不对称,该现象将导致传感器感应电动势在互补位置的幅值不等,最终影响测量精度。针对上述问题,本文提出了一种新优化思路,采用磁场补偿驱动方案提高磁场对称性和均匀性,弥补结构上的不足,以达到提高传感器测量精度的目的。

1 测量原理及数学模型搭建

1.1 双层时栅角位移传感器测量原理

双层时栅角位移传感器总体结构如图1所示,传感器由激励部分与感应部分组成,两部分均采用双层互补式结构。激励部分由节距为w的矩形线圈组成,共有6个扇区,相邻扇区相差四分之一个节距,以实现传感器激励线圈在空间上的正交,感应部分由节距为w的正弦型结构组成。

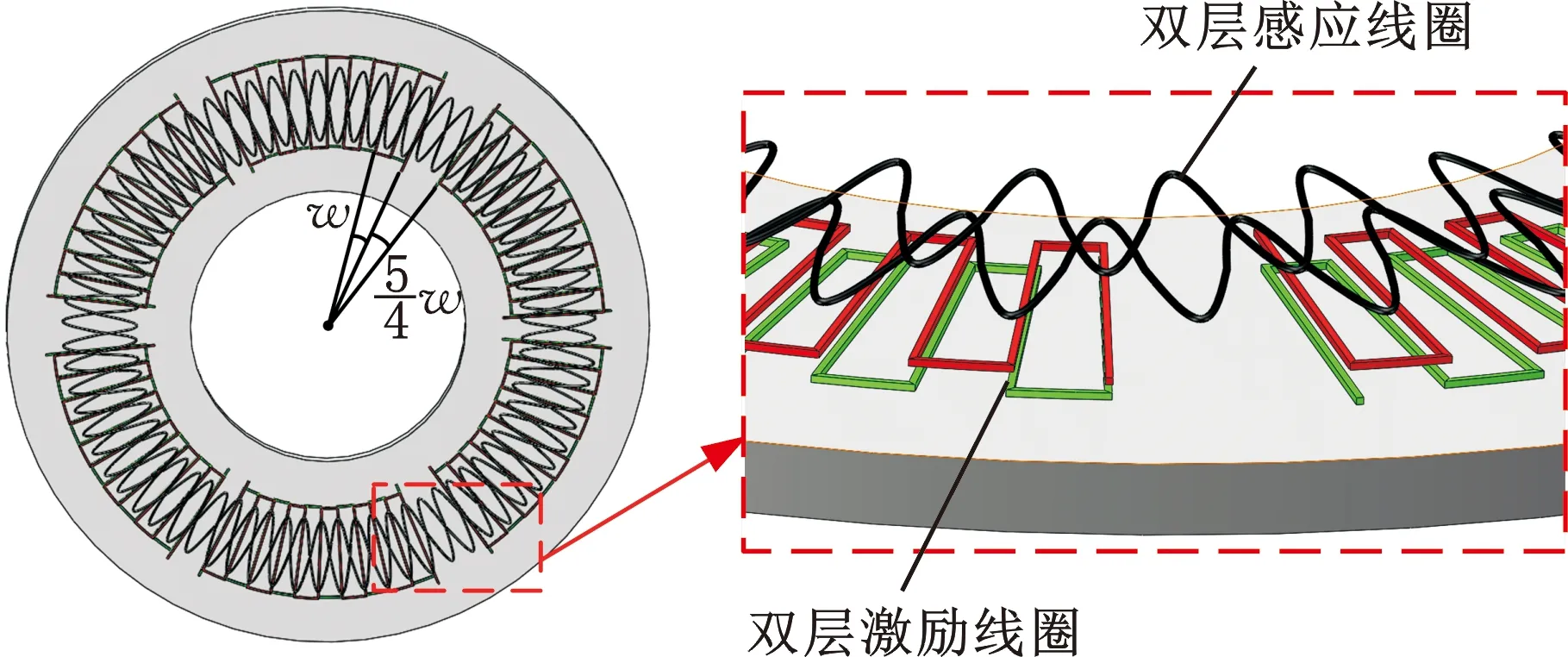
图1 双层时栅位移传感器结构示意图Fig.1 Schematic diagram of double layer time gate displacement sensor

相邻扇区激励线圈分别通入相位差为π/4的两路激励信号,以实现驱动信号在时间上的正交。传感器的测量原理如图2所示。在感应线圈所在平面上,根据毕奥-萨法尔定律对通电导线产生的磁场进行叠加形成时变磁场,图2a为感应线圈平面时变磁场分布与感应线圈内部磁通量变化示意图,其中圆点表示磁场方向为垂直平面向外,叉号表示磁场方向为垂直平面向内,Hc为感应线圈高度。由图2a可知,当感应线圈沿着X轴正方向移动θ时,此时感应线圈内部有正负磁场强度同时作用,负磁场所穿过的面积抵消了部分正磁场所穿过的面积,正好对应正弦函数阴影部分半个周期的积分形式。根据法拉第电磁感应定律,感应线圈上将感应生成一路感应电动势,感应电动势与磁通量和位移量的关系为

(1)

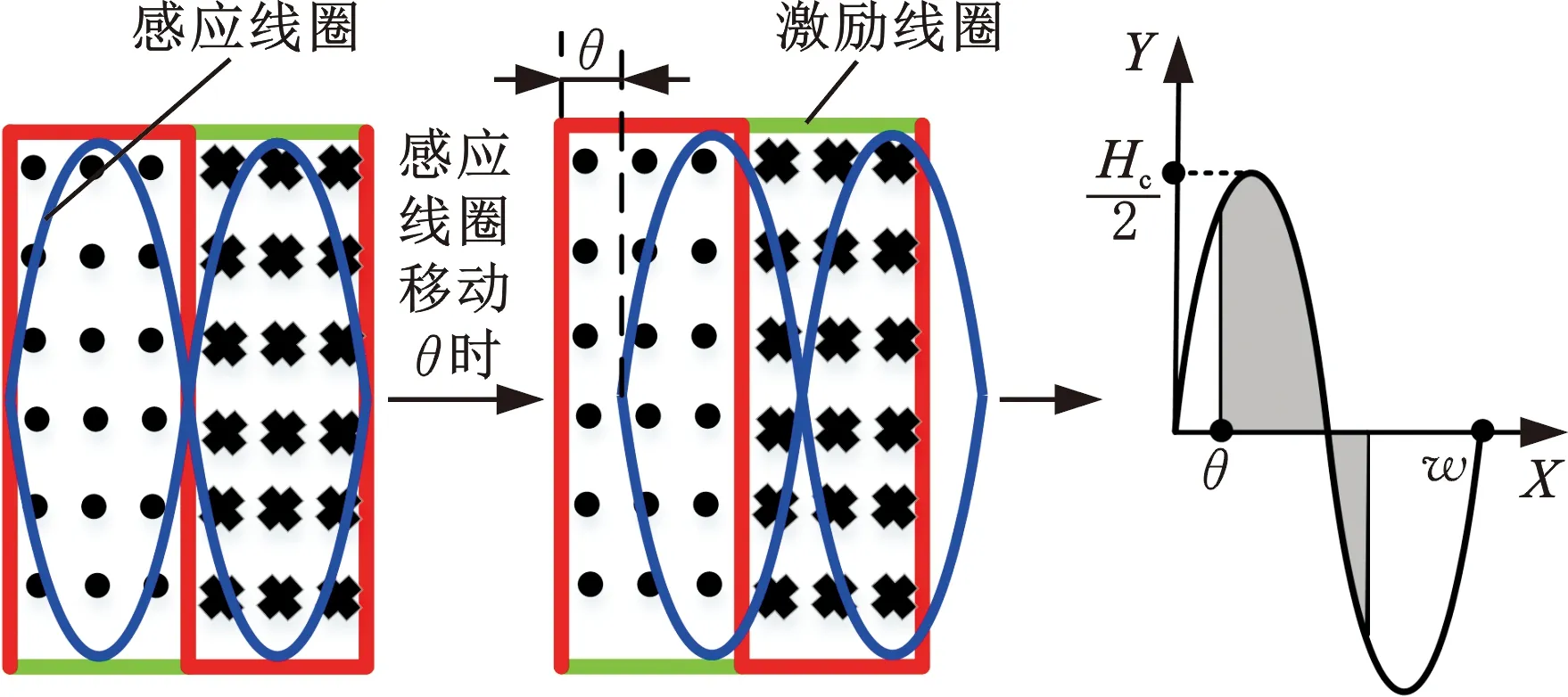
(a)时变磁场平面分布与感应线圈内部磁通量示意图

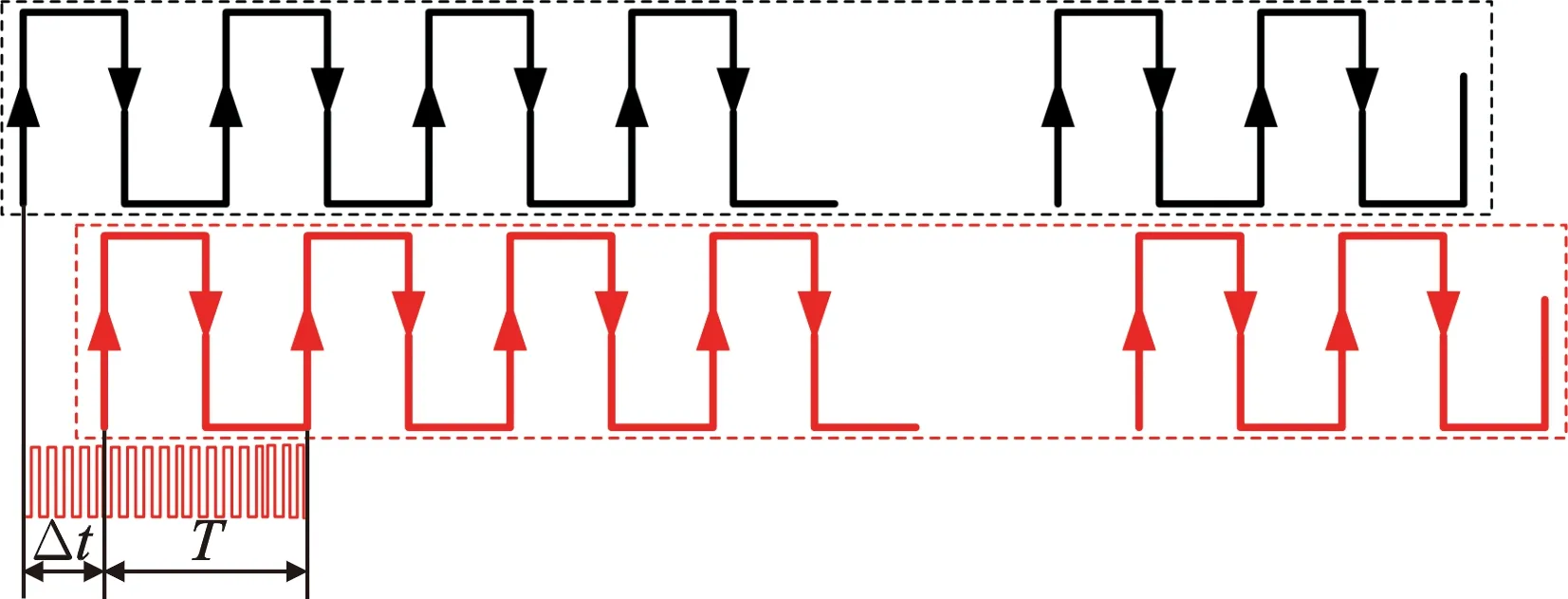
(b)传感器感应信号计时原理图2 传感器测量原理示意图Fig.2 Schematic diagram of sensor measurement principle

式中,ΔΦ为穿过感应线圈的磁通量的变化量;Δtx为位移前后时间差;K1为感应电动势的系数;ω为角频率;t为时间;w为感应线圈节距;θ为感应线圈与激励线圈的相对角位移量。

传感器激励信号在时间上正交,激励线圈结构在空间上正交,由此得出另外一路感应电动势表达式为

(2)

由于传感器感应线圈相互串联,因此传感器输出的行波信号是两路感应电动势之和,则行波信号表达式为

(3)

由式(3)可知,位移量的表达式为行波信号的相位值,因此测量行波信号与参考信号的相位差能实现位移量的解算。行波信号经过放大、滤波、整形处理之后,形成一路带有位置信息的方波信号,方波信号在处理器中与参考信号作数字信号处理,采用高频时钟插补技术测量该方波信号周期T以及与参考信号的时间差Δt,Δt与T可得相位差,从而实现对位移量θ的解算。计数原理如图2b所示。θ与Δt和T的关系可表示为

(4)

式中,M为移动节距数。

1.2 双层时栅角位移传感器数学模型

在1.1节测量原理介绍中,时变磁场均在理想的条件下进行计算,忽略了上下层激励线圈间距。本文在考虑线圈间距的基础上,重新建立双层正交型结构的数学模型,对时变磁场作进一步分析。由于传感器结构精细,在较大对极数的情况下,外径线圈弧度与内径线圈弧度近似于平行线,因此根据图1中激励线圈建立磁场仿真模型,如图3所示。线圈沿Y方向长度为2b,沿X轴方向长度为2a,两层激励线圈相距为c,在感应线圈平面内将任意场点设为P(m,n,k),场点P到导线B′C′的距离为H,P′为场点投影到OXY平面的坐标点。原有驱动方案是将上下层激励线圈进行串联并通入幅值为I的电流,P点的磁场强度由6根通电导线BC、CD、DA、D′A′、A′B′、B′C′共同叠加而成。Q为通电导线B′C′中的一点,Q点电流元在P点处产生的元磁场(元磁场方向为垂直于平面QPC′)根据毕奥-萨法尔定律可矢量表达为

(5)

式中,B为磁感应强度;μ0为真空磁导率;Idl为导线上Q点的线电流元;dl为电流的微小线元素;QP为Q点指向场点P的向量。

图3 激励线圈磁场仿真模型Fig.3 Magnetic field simulation model of excitation coil

根据图3设点Q的坐标为(a,y,0),y为Y轴上的位移,则dB可用向量的方式表示为

dB=(dBX,dBY,dBZ) =

(6)

式中,dBX、dBY、dBZ分别为沿坐标轴三个方向的分量。

由于感应线圈平面与激励线圈平面相平行,因此只需要考虑感应线圈平面的法线方向(Z轴)上的磁场dBZ。

根据三角公式可得

(7)

(8)

式中,θ1为线段B′P与线段B′C′的夹角;θ2为线段C′P与线段B′C′的夹角。

采用积分法联立式(7)和式(8)可求得通电导线B′C′在场点P处沿Z轴方向上产生的磁场强度BB′C′Z为

(9)

其中,x、z分别为X轴和Z轴上的位移。同理可得其余5条导线在场点P处沿Z轴方向上产生的磁场强度BA′B′Z、BD′A′Z、BBCZ、BCDZ、BDAZ。

由磁场叠加定理可得场点P沿Z轴方向的磁场强度为

BZ=BB′C′Z+BA′B′Z+BD′A′Z+BBCZ+BCDZ+BDAZ

(10)

2 磁场补偿驱动方案设计

2.1 磁场仿真

根据式(10)所建立的数学模型不能直观地反映时变磁场的不对称性,因此在数学模型的基础上结合MATLAB软件进行磁场仿真,仿真参数如表1所示,仿真结果如图4所示。

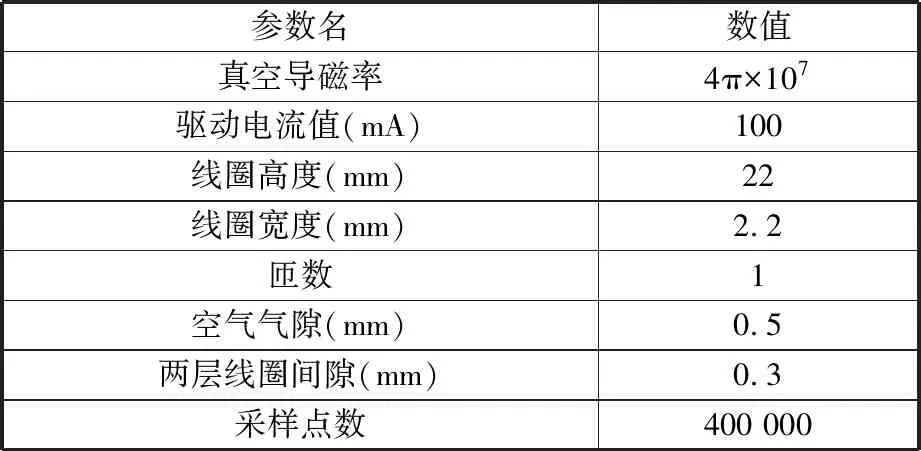
表1 仿真参数设置

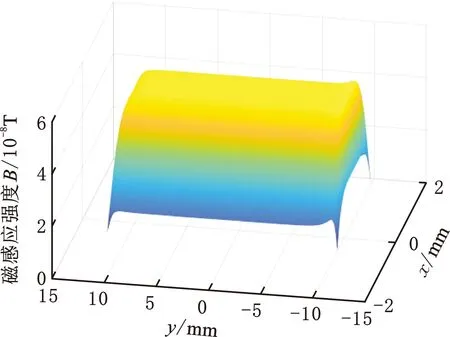
(a)磁场强度三维图

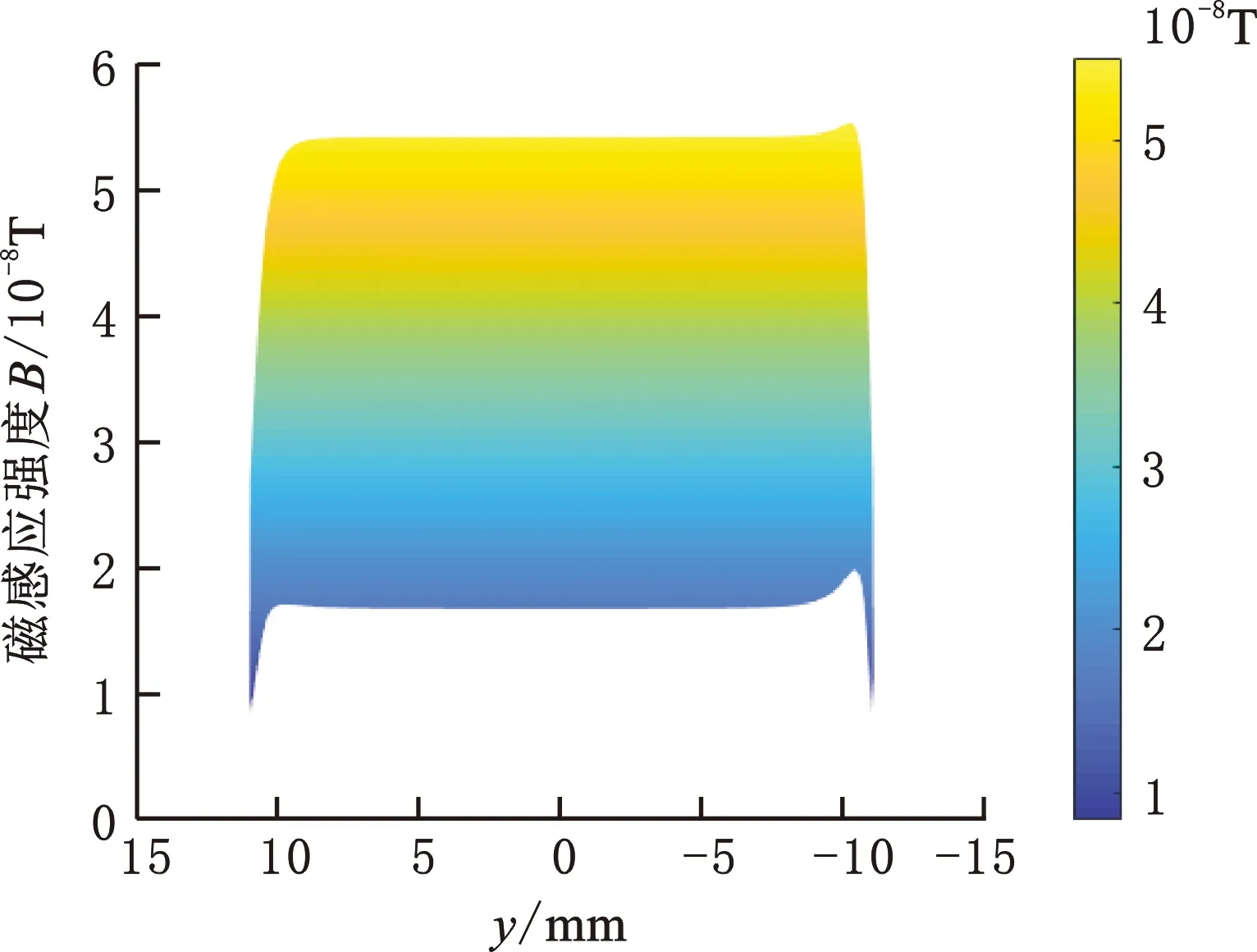
(b)沿Y轴方向平面磁场强度分布图图4 感应线圈平面磁场分布图Fig.4 Planar magnetic field distribution diagram of induction coil

由图4可知,该平面中心区域的磁场强度为5.3×10-8T,在Y方向上越靠近线圈端部磁场分布愈发不对称,若以中心区域的磁场强度为平均值时,Y方向上位于两边端部位置的磁场强度相对误差最大为10%,因此考虑线圈间距时激励线圈所产生的时变磁场分布不对称。

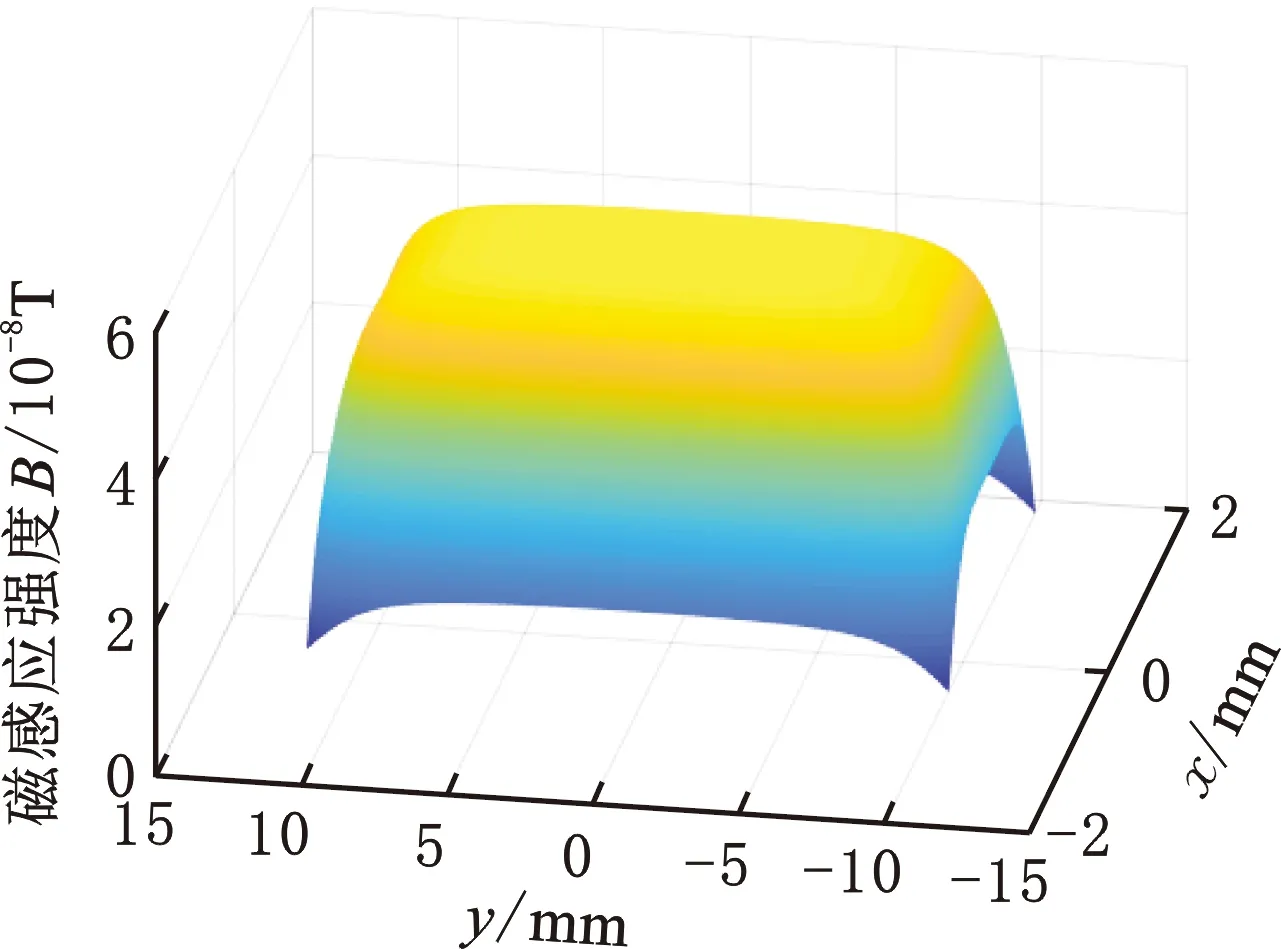
(a)磁场强度三维图(中部四根通电导线)

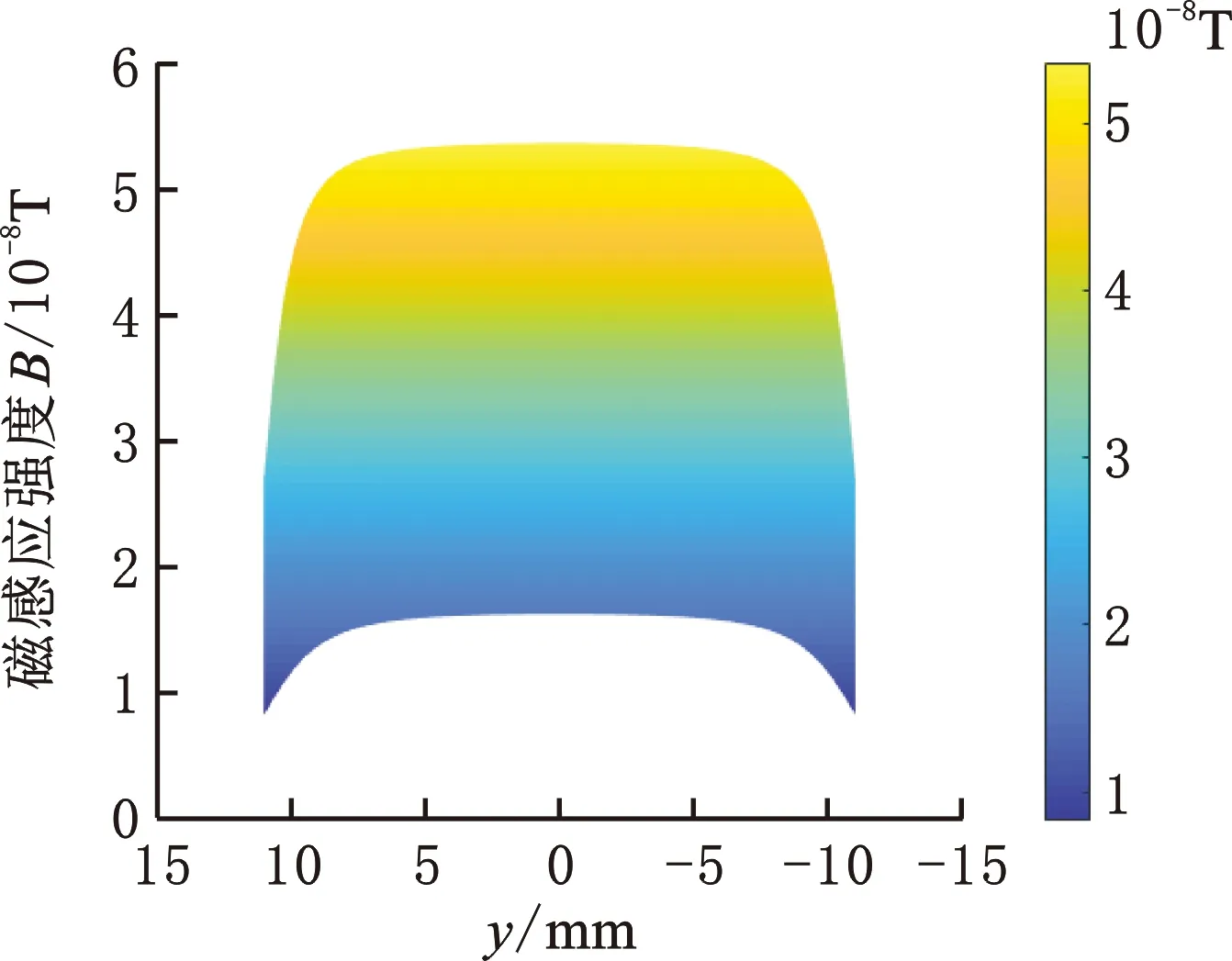
(b)沿Y轴方向平面磁场强度分布图(中部四根通电导线)

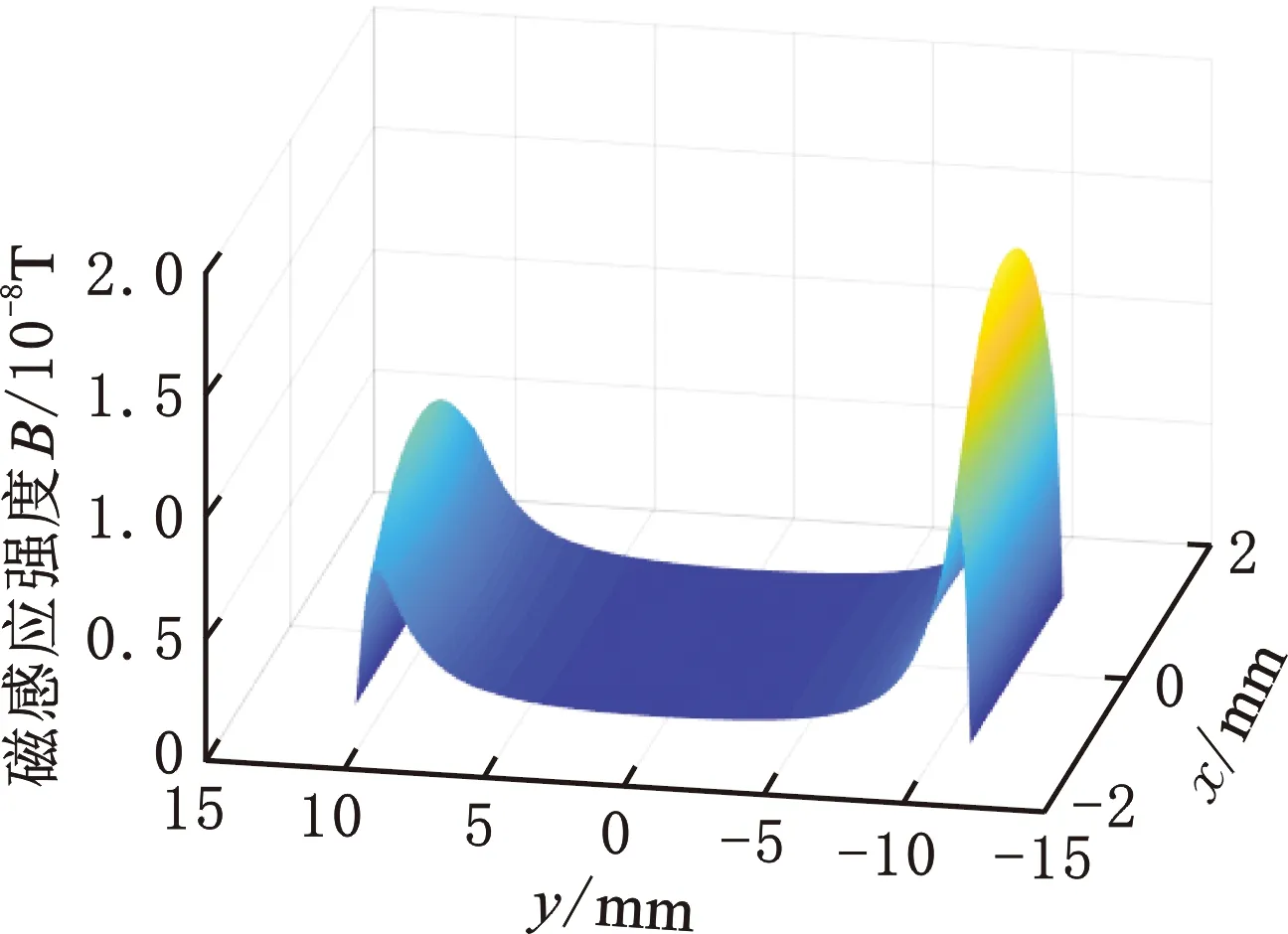
(c)磁场强度三维图(端部两根通电导线)

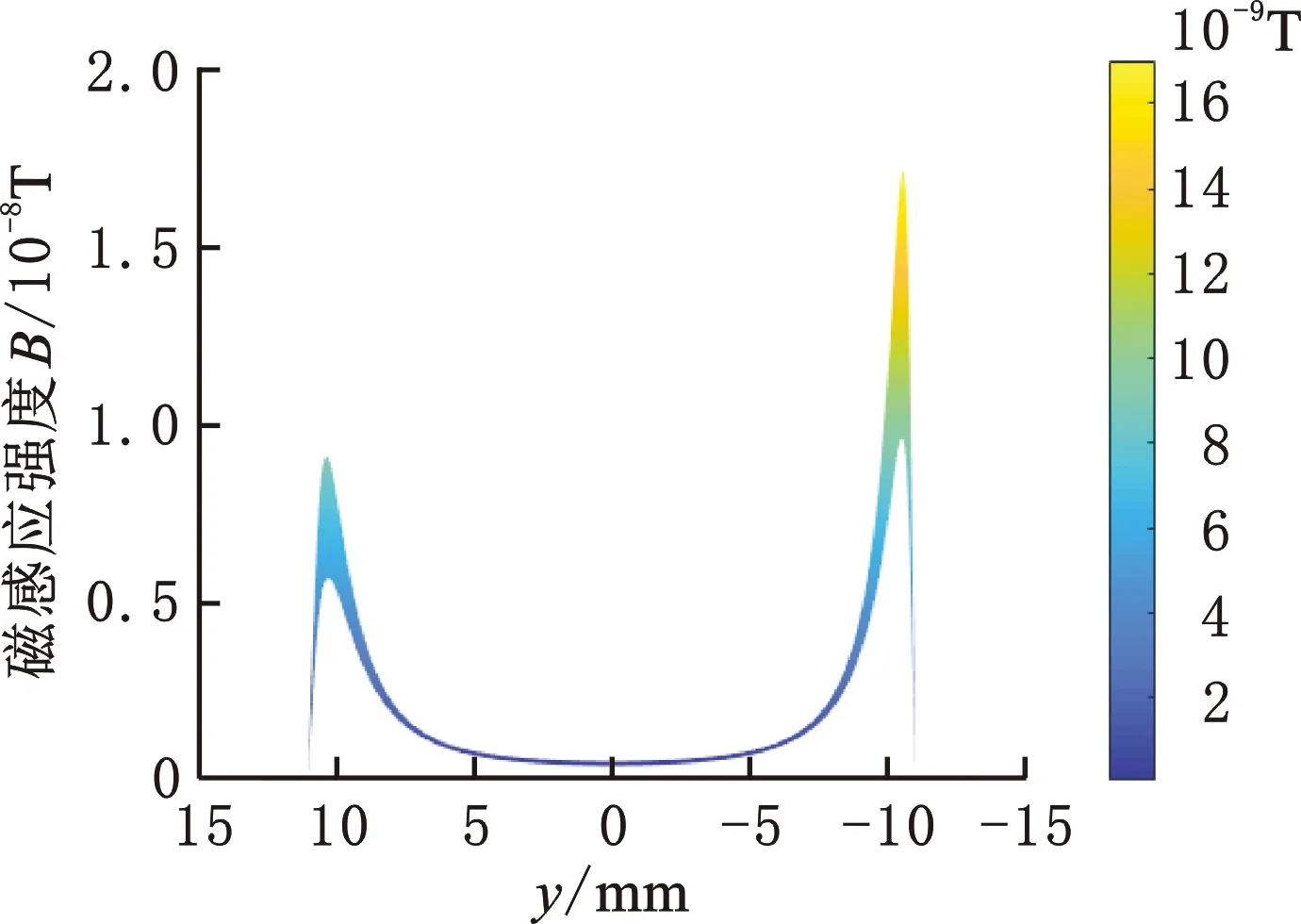
(d)沿Y轴方向平面磁场强度分布图(端部两根通电导线)图5 分层分析时感应线圈平面磁场分布图Fig.5 Planar magnetic field distribution diagram of induction coil during stratified analysis

为进一步分析导致该现象的因素,对激励线圈进行了分层讨论,上层激励线圈与下层激励线圈各自单独作用时的磁场分布如图5所示。上层线圈lD′A′和lB′C′与下层线圈lBC和lDA产生的磁场分布分别如图5a和图5b所示,从图中可知中部四根通电导线在感应线圈平面产生的磁场强度约为5.3×10-8T,四根导线所产生的磁场关于坐标轴对称,由此可知这四根导线并不是导致磁场不对称的原因。图5c、图5d所示分别为导线lA′B′和lCD通入相同激励电流时在感应平面所产生的磁场强度,从图中可以看出,两根通电导线在感应平面产生的磁场强度左右不对称,这是由于lA′B′和lCD位于端部远离中心区域,在线圈中部影响不大,只对接近端部的磁场影响较大,且上层端部线段lA′B′产生的磁场强度较大,约为1.7×10-8T,因此可以得出影响磁场不对称的因素为不在同一平面的两根通电导线lA′B′和lCD。

2.2 磁场补偿式驱动方案与结构参数的关系

根据磁场强度表达式,感应线圈所在平面的磁场强度与激励线圈高、激励线圈宽、空气间隙、上下层线圈间距以及驱动电流有关。传感器结构与各个参数相对应,其中线圈高、线圈宽和上下层线圈间距与传感器线圈结构有关。当传感器结构确定时,感应平面上的磁场强度仅与电流相关。

通过对6条通电导线的磁场分析可知,远离感应线圈平面的通电导线lCD产生的磁场强度弱于lA′B′产生的磁场强度,最终导致时变磁场不对称。为了解决时变磁场不对称的问题,通过增大下层激励线圈电流使得下层感应线圈磁场强度增大,以抵消通电导线与lCD所产生的不对称磁场,并以此作为磁场补偿式驱动方案的核心思想。当传感器的结构确定时各个参数均已确定,则感应平面场点磁场强度表达式为关于x与y的二元二次表达式,可以根据关于二元二次的极值求解方法求得中部磁场强度的最大值及其对应坐标A(x1,y1),同理可得整个结构在端部所产生的磁场最大值及其对应坐标B(x2,y2),将A和B点的磁场强度分别作为中间部分磁场强度和端部的磁场强度的参考点,增大下层线圈电流使得A、B两点磁场强度相等,以达到抵消端部磁场的不对称性的目的。

将下层激励线圈电流设为I2,则生成的新的磁场强度BZ1为

BZ1=BB′C′Z+BA′B′Z+BD′A′Z+

(BBCZ+BCDZ+BDAZ)I2/I

(11)

根据磁场补偿驱动方案的核心思想可得

BZ1(x1,y1)=BZ1(x2,y2)

(12)

结合式(11)和式(12)即可得电流I与I2的关系表达式为

I2=I(BB′C′Z(x1,y1)+BA′B′Z(x1,y1)+

BD′A′Z(x1,y1)-BB′C′Z(x2,y2)+BA′B′Z(x2,y2)+

BD′A′Z(x2,y2))/(BBCZ(x2,y2)+BCDZ(x2,y2)+

BDAZ(x2,y2)-BBCZ(x1,y1)+BCDZ(x1,y1)+

BDAZ(x1,y1))=If(a,b,c,z)

(13)

其中,f(a,b,c,z)表示关于传感器结构参数的函数。将表1中的结构参数代入式(13),可求得I2为118 mA。

为了验证磁场补偿思路的可行性,将得出的电流幅值结合仿真模型再次进行磁场仿真,设置的参数如表2所示,磁场分布如图6所示,由图可知,当下层激励线圈电流为118 mA时磁场强度增大到5.8×10-8T,磁场强度相对误差减小为0.3%。对比图4可知,与原有的驱动方案相比,利用这种磁场补偿驱动方案得到的磁场分布更加对称,可以抵消端部导线所带来的磁场不对称性。

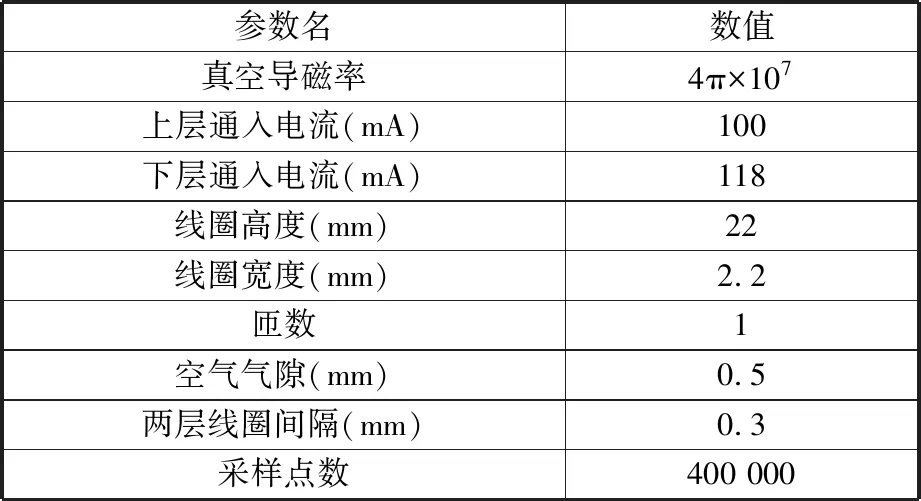
表2 磁场仿真参数设置

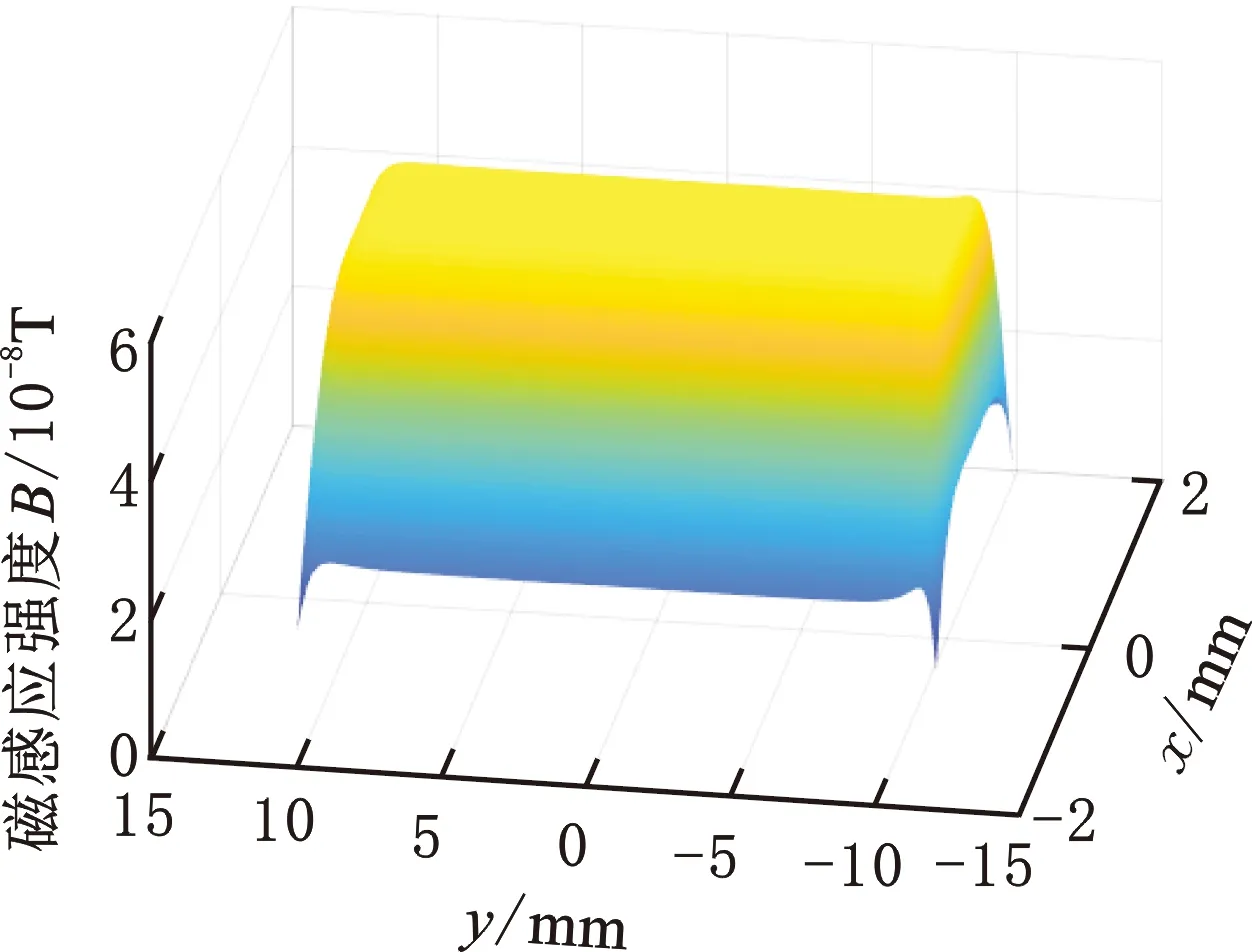
(a)补偿后磁场强度三维图

(b)补偿后沿Y轴方向平面磁场强度分布图图6 补偿后感应线圈平面磁场分布图Fig.6 Magnetic field distribution diagram of induction coil after compensation

3 有限元仿真与误差分析

3.1 有限元对比仿真

根据第2节的磁场仿真结果,实际情况下传感器节距内时变磁场存在不对称,但在测量原理中磁场强度均是采用理想状态下的均匀磁场进行计算的。根据式(1)所示的感应电动势的表达式,当传感器感应线圈处于激励线圈节距内的互补位置时,面积变化量不变,但传感器激励线圈节距内时变磁场并不是呈理想的对称分布,从而造成感应信号在互补位置时幅值不相等。实际情况下两路感应电动势为

(14)

(15)

式中,kc为互补位置的幅值差值。

由于行波信号是由两路感应电动势合成的,则合成后的行波信号可表示为

(16)

式中,K为行波信号的幅值;φ1、φ2为行波信号的相位值。

根据三角函数变化可得

(17)

根据式(16)、式(17)得出,不对称时变磁场影响了相位差,进一步导致解算出来的位移量出现偏差,因此为了验证磁场补偿驱动方案的可行性,采用分析软件Maxwell对传感器的结构模型进行有限元仿真,分析该方案对感应电动势幅值以及测量误差的影响,仿真结构模型如图1所示。本文的仿真采用两种不同驱动方案进行对比,仿真参数如表3所示,仿真结果如图7所示。

表3 有限元仿真参数

(a)正弦信号激励感应电动势

(b)余弦信号激励感应电动势

(c)行波信号图图7 感应电动势与行波信号图Fig.7 Induced electromotive force and traveling wave signal diagram

3.2 误差分析

仿真产生两路感应电动势,每一路有50个采样点。根据感应电动势的表达式,感应电动势的幅值与空间位移量和节距有关,一个节距内转子在互补位置时幅值相等符号相反。取25对互补位置的感应电动势幅值进行取模作差,两种不同驱动方式下互补位置的感应电动势幅值相对误差如图8所示。

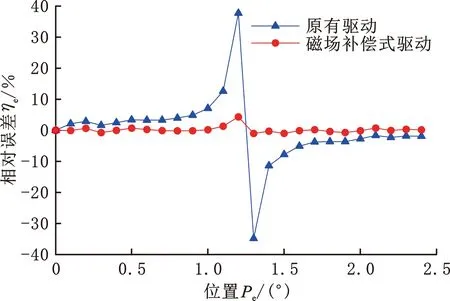
图8 互补位置感应电动势幅值误差Fig.8 Amplitude error of complementary position induced electromotive force

由图8可以看出,不同驱动方案下感应电动势幅值差值曲线的变化趋势相似,原有驱动方案激励下,幅值的相对误差整体偏大,最大值出现在1.3°,磁场补偿驱动方案激励时,互补位置的感应电动势幅值相对误差明显减小,说明磁场补偿驱动方案可以减小转子在互补位置上感应电动势的幅值相对误差。

通过将两路感应电动势相加可得带有位置信息的行波信号,如图7c所示。根据图2中的求解原理可得行波信号的相位差与传感器的位移量。故可将0°位置处行波信号的相位作为初始相位值,以此计算每个角度行波信号的相位与初始相位的相位差,进而求解出各个角度相对于0°位置的相对位移。将测量位移量与真实位移量作比较可得每个位置的角度误差。两种不同驱动方案激励时传感器模型的角度误差曲线见图9。

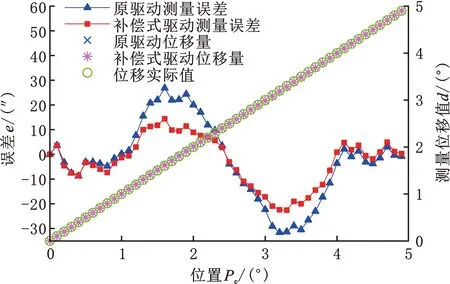
图9 两种不同驱动方案下传感器误差曲线Fig.9 Sensor error curves under two different driving schemes

由图9可知,两种驱动方案驱动时误差曲线呈相同的周期性变化,当磁场补偿驱动方案作用时,转子在1.3°～2.4°与2.9°～4°时测量误差明显减小。从仿真数据分析中可以得到,没有补偿电流时,测量误差范围为(-31.6″,26.9″),当有补偿电流作用时测量误差范围为(-22.4″,14.2″)。由此可以得出,当磁场补偿驱动方案激励时测量误差峰峰值从之前的58.5″变为36.6″,误差峰峰值减小了37.4%。

4 实验验证

4.1 实验台的搭建

根据图1中的传感器结构模型,采用PCB工艺加工传感器样机。安装时栅角位移传感器并搭建对比实验平台,为测量时栅角位移传感器精度,采用更高精度等级的海德汉光栅进行误差标定,光栅型号为RON-866,传感器整周刻有36 000个栅线,系统精度为±1″;采用电子细分盒处理光栅输出信号,可以将光栅分辨率提高100倍。安装时将角位移编码器与时栅角位移传感器同轴安装,从而使两者同步运动,信号处理电路同步采集两个传感器数据,通过串口上传到上位机进行误差标定,实验现场如图10所示。

图10 双层时栅角位移传感器对比实验台Fig.10 Double layer time grating angular displacement sensor contrast experimental platform

4.2 对比实验

双层时栅角位移传感器驱动频率为10 kHz,根据磁场补偿驱动方案可得两层驱动电压分别为4.25 V和5.02 V,本次实验将两层驱动电压设置为4.3 V和5.0 V进行驱动,与原有驱动方案中上下层驱动电压均为4.3 V展开对比实验。设置一个节距内采样点个数为50,得到不同驱动方案下的误差曲线见图11。

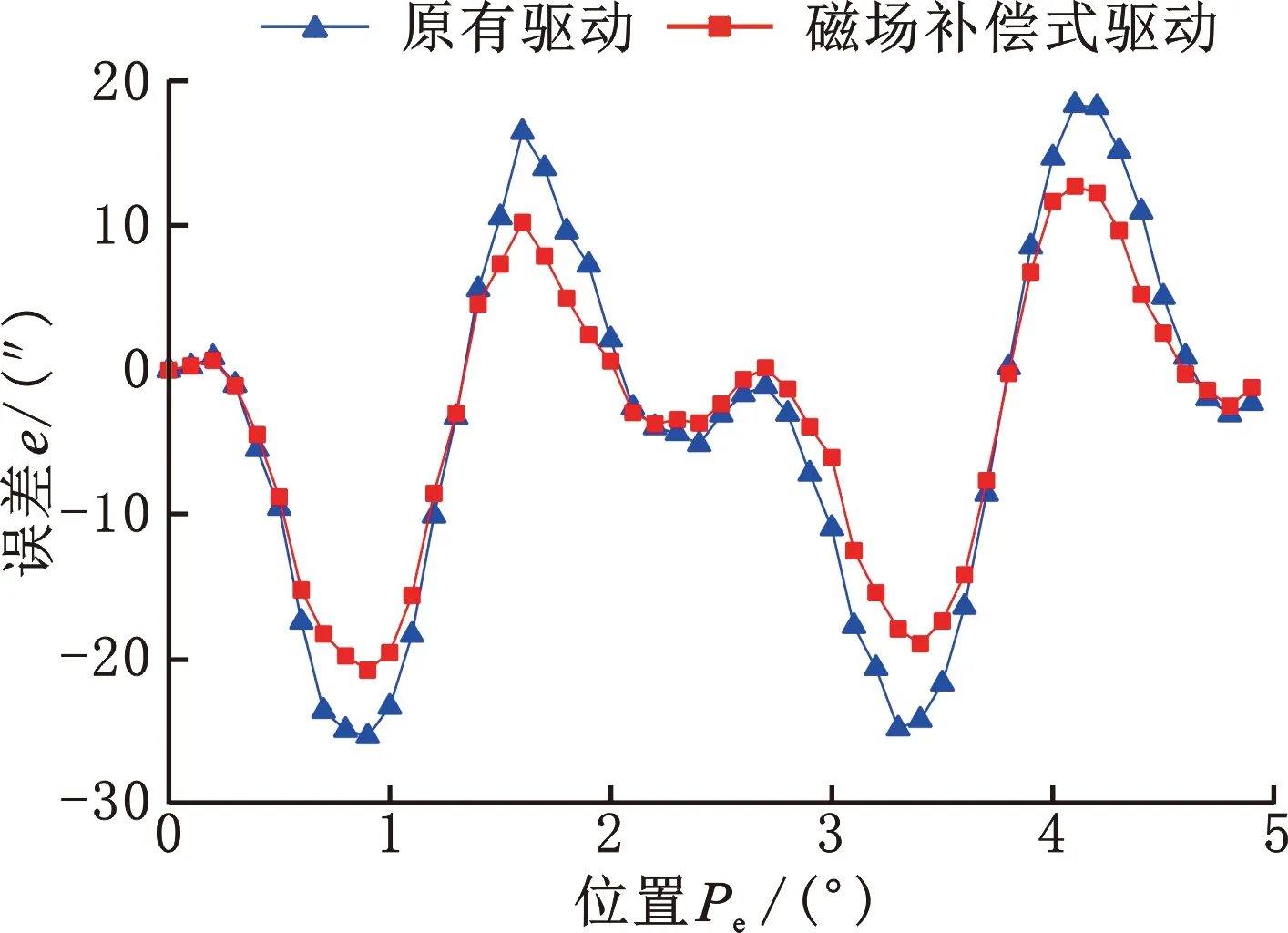
图11 节距内实验误差曲线对比Fig.11 Comparison of error curves in polar experiment

实验误差曲线表明,节距内测量出的误差从(-25.5″,18.3″)减小到(-20.8″,12.6″),磁场补偿驱动方案提高了传感器测量精度,实验结果与仿真结果基本一致。

5 结论

(1)本次研究通过对双层时栅角位移传感器结构建模与时变磁场的仿真,发现上层激励线圈与下层激励线圈的间隙会对时变磁场产生影响,从而导致在互补位置时感应电动势幅值不等。由此引出一种磁场补偿驱动方案,该方案将上下两层激励线圈通入不同幅值电压以消除间隙对时变磁场的影响,通过磁场补偿思路与传感器的结构参数确定了与之对应的上下层激励线圈驱动电压关系。同时经过数学分析、建模仿真、实验对比,验证了磁场补偿驱动方案的有效性。该驱动方案提高了行波磁场的对称性,经对比研究后,节距内测量误差从(-25.5″,18.3″)减小到(-20.8″,12.6″)。

(2)本次研究更贴近实际情况下的传感器研究,通过优化驱动方案来弥补结构上的不足,并且适用于不同结构参数的双层时栅位移传感器,为高精度传感器优化设计提供了新思路。