永磁轨道参数优化和悬浮力特性研究

张明亮 杨大伟 李明远 杨新梦 刘丽茹 张连朋

1.石家庄铁道大学机械工程学院,石家庄,050043 2.西南交通大学轨道交通运载系统全国重点实验室,成都,610031 3.兰州交通大学光电技术与智能控制教育部重点实验室,兰州,7300704.中国铁路哈尔滨局集团有限公司三棵树车辆段,哈尔滨,150000

0 引言

区别于传统轮轨交通技术,高速磁悬浮列车依靠磁力进行悬浮导向、利用直线电机进行驱动,能够摆脱轮轨和弓网对运行速度的限制[1],因此,磁悬浮轨道交通技术具有运行速度快、安全、环保等诸多优点,受到很多国家的青睐,投入了大量的资金进行科学研究[2]。按照磁悬浮原理的不同,磁悬浮技术主要分为4类:常导电磁悬浮、电动磁悬浮、高温超导钉扎磁悬浮、永磁磁悬浮[[3-5]。常导电磁悬浮技术是基于铁磁原理,依靠车载电磁铁与铁磁性轨道之间的磁吸力来平衡重力,通过反馈控制电磁铁的电流使车体稳定悬浮;电动磁悬浮又分为永磁铁作为磁源的永磁电动磁悬浮和低温超导线圈作为磁源的低温超导电动磁悬浮,两者都是基于楞次定律,依靠车载磁体与轨道线圈相对运动时轨道线圈产生感生电流,电流产生磁场,与车载磁体的磁场之间产生磁力从而平衡重力,使车体稳定悬浮;高温超导钉扎磁悬浮是基于高温超导体在混合状态时特有的磁通钉扎效应,使永磁轨道(permanent magnet railway,PMR)部分磁场被高温超导体捕获而产生引力,同时由于其抗磁性而产生斥力,引力和斥力与重力相互作用,使高温超导体能够稳定悬浮在永磁轨道上方[6-9];永磁磁悬浮利用同性相斥原理产生斥力来平衡重力,使车体稳定悬浮。以上4类磁悬浮各有优缺点,常导电磁悬浮结构较简单,但控制精度要求高;永磁电动磁悬浮不需要低温环境,但磁力较小,低温超导电动磁悬浮的悬浮高度大,但需要极低温度(液氦4K);高温超导钉扎磁悬浮无需控制自稳定,但永磁轨道铺设较昂贵;永磁磁悬浮作用力较大,但侧向不稳定,需辅助接触装置,影响悬浮效果。针对上述优缺点,本文选择高温超导钉扎磁悬浮进行研究。

自1911年发现超导现象以来,超导材料不断发展,随着超导材料的临界温度、临界电流、临界磁场等性能不断提高和完善,尤其是高温超导材料性能的提升,人们能够较低成本地开展超导应用技术的研究,其中一个重要领域便是高温超导钉扎磁悬浮列车的研究[10-13]。早期磁悬浮研究以结构简单的单峰永磁轨道为磁源[14-15],直至2008年,DENG等[16]提出一种基于“Halbach”阵列的双峰永磁轨道,并将单峰永磁轨道与Halbach型双峰永磁轨道进行比较,结果表明双峰永磁轨道具有明显的优势。JING等[17]提出了一种“T”形轨道,但因其稀有材料用量多造成造价成本高,从而未进行深入探究。随后永磁轨道的研究集中于Halbach型双峰型永磁轨道,里约热内卢联邦大学小组提出一种磁场较平滑的“Halbach”型永磁轨道,但其悬浮效率较低[18]。HEKMATI等[19]提出通过改变磁化角度来优化永磁轨道的新思路,并对已有的Halbach型双峰永磁轨道进行了分析。梁星等[20]研究了三极对顶式永磁轨道(即双层单峰轨道)表面磁感应强度,得到中间纯铁越薄、下方永磁体越长,磁感应强度越大的结论。高温超导钉扎磁悬浮列车配对使用的永磁轨道主要包括单峰结构和双峰结构,学者们对其磁场性能进行了比较分析[21-23]。

永磁轨道磁场大小及分布直接决定着该类磁悬浮系统的悬浮能力,悬浮力的大小直接决定列车载重的能力。任仲友等[24]研究了单峰型永磁轨道与YBCO(钇钡铜氧)高温超导体之间的悬浮力,研究发现,轨道中心的磁场强度和磁场梯度与悬浮力成正比关系,悬浮间距与悬浮力成反比例关系。任仲友等[25]也研究了超导体横向偏移与导向力之间的关系,研究发现,当超导体宽度略大于永磁轨道宽度时,导向力不再继续增大。申政等[26]研究得到高温超导块与永磁体之间间隙越小、两者的半径越大、永磁体的厚度越大,则磁悬浮力越大的结论。吴爽等[27]研究表明,当永磁体和高温超导体截面相同时捕获磁场最大,从而悬浮力也最大。其他多位学者也对永磁轨道磁场进行研究,也得出了磁场越大悬浮力越大的结论[28-31]。

尽管目前对永磁轨道的磁场进行分析的研究较多,但对其综合性能指标对比研究较少。本文选用能提供较强磁场的Halbach型双峰永磁轨道为研究对象,以磁场综合性能最佳为目标,基于田口正交法对永磁轨道的多个影响因素进行优化,寻求最佳参数组合。然后基于冻结镜像模型[32]提出等效处理高温超导体的方法(简称等效处理方法),计算高温超导体和永磁轨道之间的悬浮力,并通过实验验证方法的正确性。

1 高温超导钉扎磁悬浮列车的工作原理

高温超导钉扎磁悬浮列车主要由车载高温超导体及冷却系统、地面永磁轨道与驱动系统组成,高温超导体和永磁轨道间通过磁通钉扎效应产生相互作用从而提供悬浮力和导向力,驱动系统提供前进动力[33-35]。高温超导体经过液氮(-196 ℃)冷却后由常态转化为超导态,产生特有的磁通钉扎效应,使其同时具有捕捉磁场和抵抗磁场的特点,即在外磁场中高温超导体能捕捉部分磁场,使其通过钉扎点,同时未被捕获的磁场很难穿透超导体。其原因在于位错、沉淀物等使高温超导体内部产生了位能势阱,位能势阱能捕捉部分磁通线同时阻止另一部分磁通线进入,其示意图见图1。

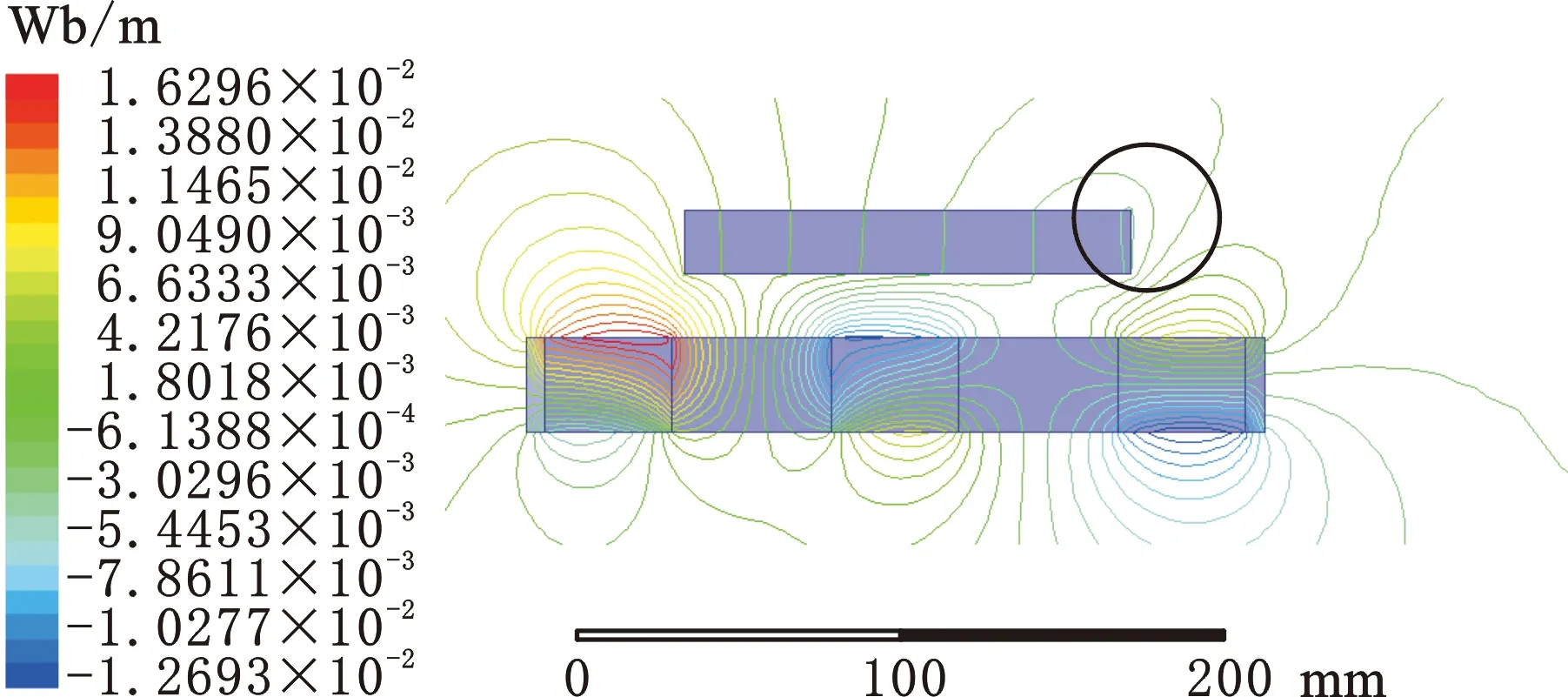
图1 高温超导体磁通钉扎效应示意图Fig.1 Schematic diagram of high temperature superconductor flux pinned effect

当高温超导体在重力作用下产生位移变化时,在钉扎中心点周围超导区域因磁场的变化将感生强电流,超导强电流产生的磁场与外磁场相互作用,作用力除与重力平衡的悬浮力外,还有能够提供横向稳定所需的导向力[27,36]。永磁轨道为高温超导体提供磁源,是高温超导钉扎磁悬浮列车的重要组成部分[37],故本文首先对永磁轨道进行优化研究。

2 Halbach型双峰永磁轨道磁场仿真及参数优化

2.1 磁场正交设计分析

为了得到更大的悬浮力,通常采用Halbach型双峰永磁轨道。该轨道由永磁体A、永磁体B和纯铁组成,其中所有的永磁体A尺寸相同,所有的永磁体B尺寸相同,两边为纯铁,充磁方向(箭头方向)如图2所示。其磁感应强度云图和磁力线分布如图3和图4所示。

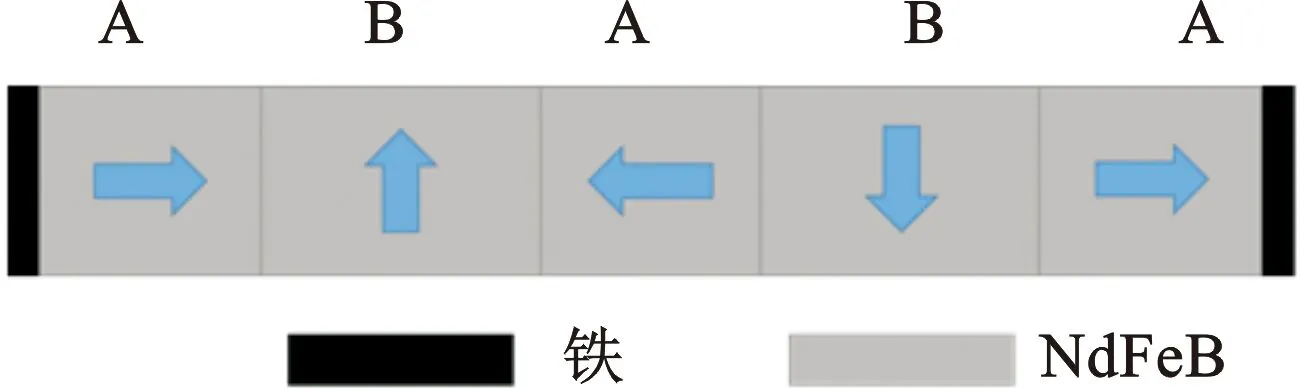
图2 Halbach型双峰永磁轨道结构示意图Fig.2 Schematic diagram of Halbach type bimodal PMR structure

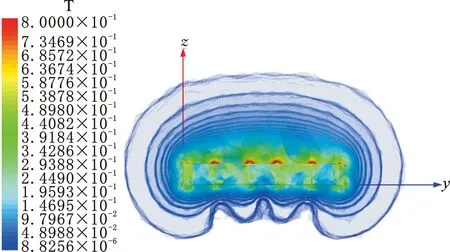
图3 Halbach型双峰永磁轨道磁感应强度云图Fig.3 Cloud image of magnetic induction of Halbach type bimodal PMR

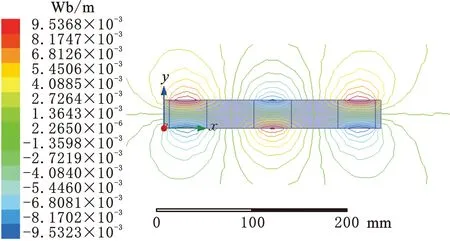
图4 Halbach型双峰永磁轨道磁力线分布图Fig.4 Magnetic field lines distribution of Halbach type bimodal PMR

由图3和图4可以观察到,双峰轨道主要磁场集中在中间位置。为更好地量化磁场特性,本文将其中一块纵向充磁永磁体上20 mm处的磁场作为磁场评估线,同时为避免断面效应的影响,截取中间线段上的平均磁感应强度Bda作为评价指标。

为了评估双峰永磁轨道材料对磁场的贡献,需计算单位质量平均磁感应强度Bdam。在此需要得到Halbach型双峰永磁轨道的质量,其计算公式如下:

md=3ρ1bdA1hdld+2ρ1bdB1hdld+2ρ2bd2hdld

(1)

式中,ρ1为永磁铁的密度;ρ2为纯铁的密度;bdA1为双峰永磁轨道中永磁体A截面的宽度;hd为双峰永磁轨道截面的高度;ld为双峰永磁轨道的长度;bdB1为双峰永磁轨道中永磁体B截面的宽度;bd2为双峰永磁轨道中纯铁截面的厚度。

由此可以得到双峰永磁轨道的单位质量平均磁感应强度:

(2)

田口方法是以正交表为基本工具,将工程经验与统计原理相结合的一种数据分析方法,它可以确定出使产品稳健的最优控制因子组合。采用田口方法可以大大缩短研发时间并能确保产品质量。基于田口正交方法利用4因子5水平对双峰永磁轨道参数进行优化,在试验中4个因子设为A截面宽度(bdA1)、B截面宽度(bdB1)、截面高度(hd)和纯铁厚度(bd2),同时根据后续悬浮力实验用的永磁轨道参数确定每个因子的5水平,在此需要进行25次试验,即L25型试验。根据式(1)和式(2)结合有限元法仿真得到不同工况(L25)下磁场性能结果,见表1。

2.2 磁场性能对比

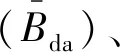
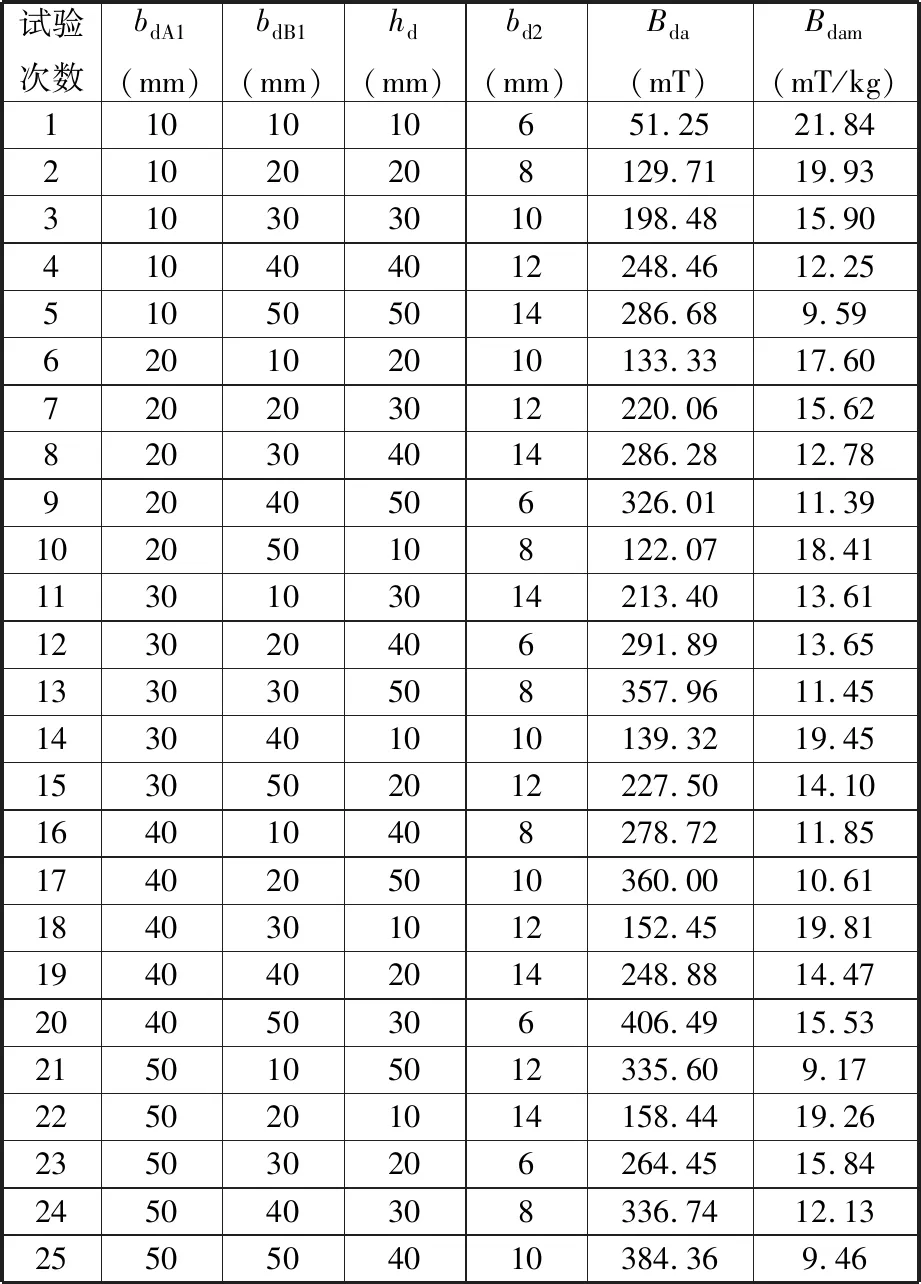
表1 双峰永磁轨道田口正交试验结果

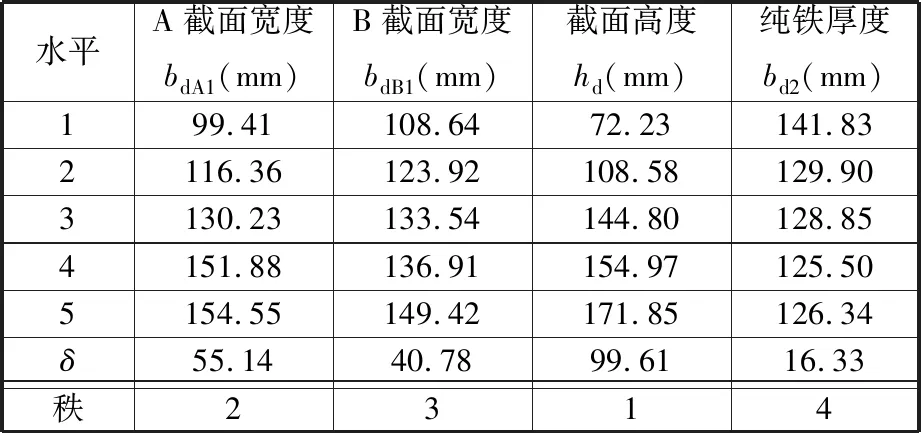
表2 平均磁感应强度均值响应表

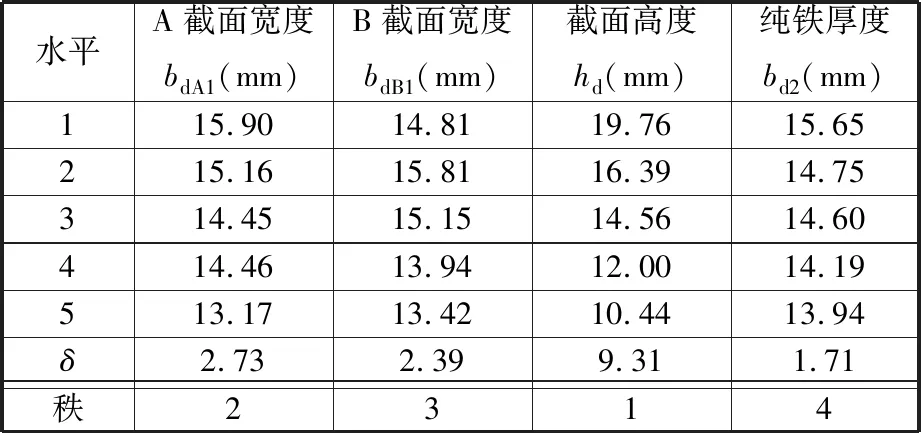
表3 单位质量平均磁感应强度均值响应表

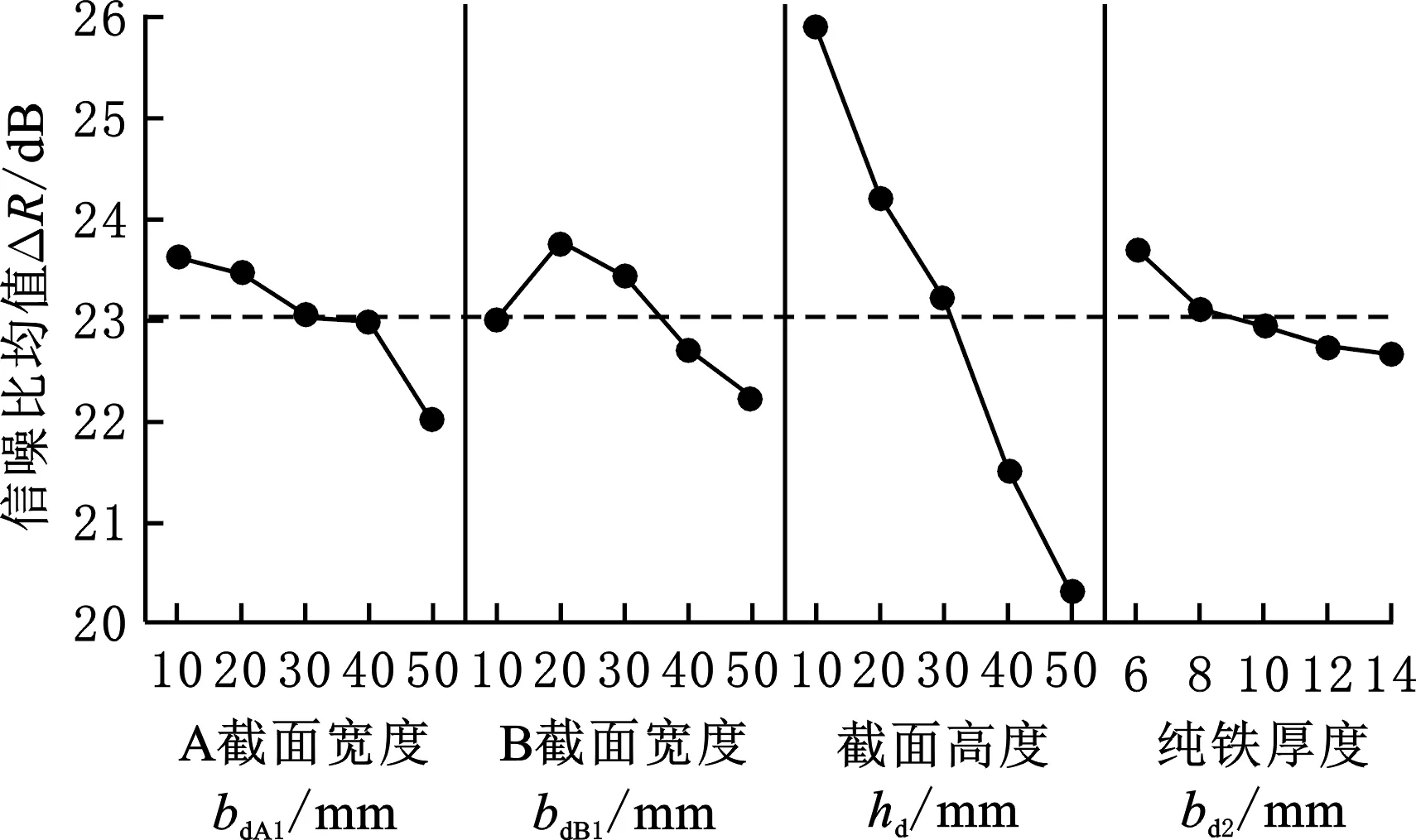
图5 平均磁感应强度信噪比主效应图Fig.5 Main effect plot of the mean magnetic induction intensity SNR

图6 单位质量平均磁感应强度信噪比主效应图Fig.6 Main effect plot of average magnetic-to-induced intensity SNR per unit mass

由表2、表3可以观察到截面高度秩都为1,A截面宽度秩都为2,B截面宽度秩都为3,纯铁厚度秩为都4,表明对平均磁感应强度和单位质量平均磁感应强度的影响顺序为hd>bdA1>bdB1>bd2。

要确定平均磁感应强度、单位质量平均磁感应强度指标响应结果与模型中因子之间的关联在统计学意义上是否显著,需将该项的P值与显著性水平进行比较,通常显著性水平为0.05。显著性水平大于0.05表示该因子为不显著影响因子,小于0.05表示该因子为显著影响因子。根据表1的数据得到标准差响应表,见表4、表5。

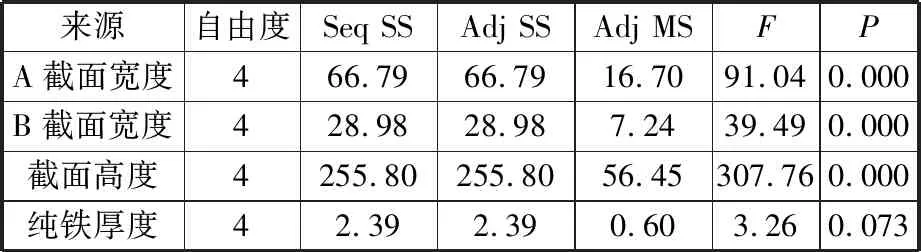
表4 平均磁感应强度标准差响应

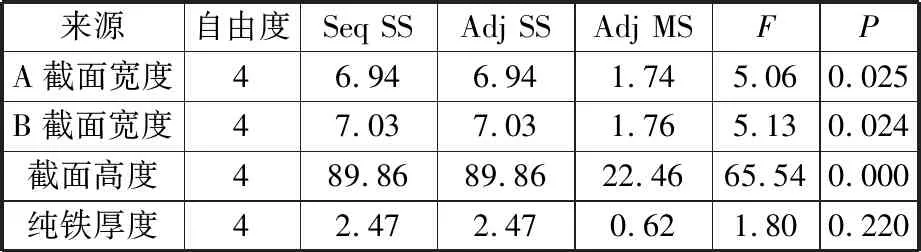
表5 单位质量平均磁感应强度标准差响应

由表4、表5中连续平方和(Seq SS)、调整平方和(Adj SS)、调整均方和(Adj MS)用于计算P值。可以观察到纯铁厚度的P值分别为0.073、0.220,已经大于0.05,表明纯铁厚度对指标响应的影响不明显,其余因子都小于0.05,故都对平均磁感应强度、单位质量平均磁感应强度影响显著。为了验证上述分析的正确性,分析了信噪比主效应图(图7、图8)。由图7、图8可以观察到,残差的正态概率图(图7a,图8a)大致为一条直线,正态概率图用来验证残差呈正态分布的假设;由残差与拟合值图(图7b、图8b)可看出残差在“0”的两端随机分布,残差数值点中无可辨识的模式,残差与拟合值图可验证残差随机分布且具有常量方差的假设;残差的直方图(图7c,图8c)无朝着一个方向的长尾与远离其他条形的状态,使用残差的直方图可确定数据是偏斜的还是包含异常值;残差与观测值顺序图(图7d、图8d)中残差围绕中心线随机分布,验证了残差具有独立性的假设。图7、图8无异常情况,表明上述分析是正确的。

(a)正态概率图

(b)残差与拟合值图

(c)残差直方图

(d)残差与观测值顺序图图7 平均磁感应强度信噪比残差图Fig.7 Residual map of the SNR of mean magnetic induction intensity

(a)正态概率图

(b)残差与拟合值图

(c)残差直方图

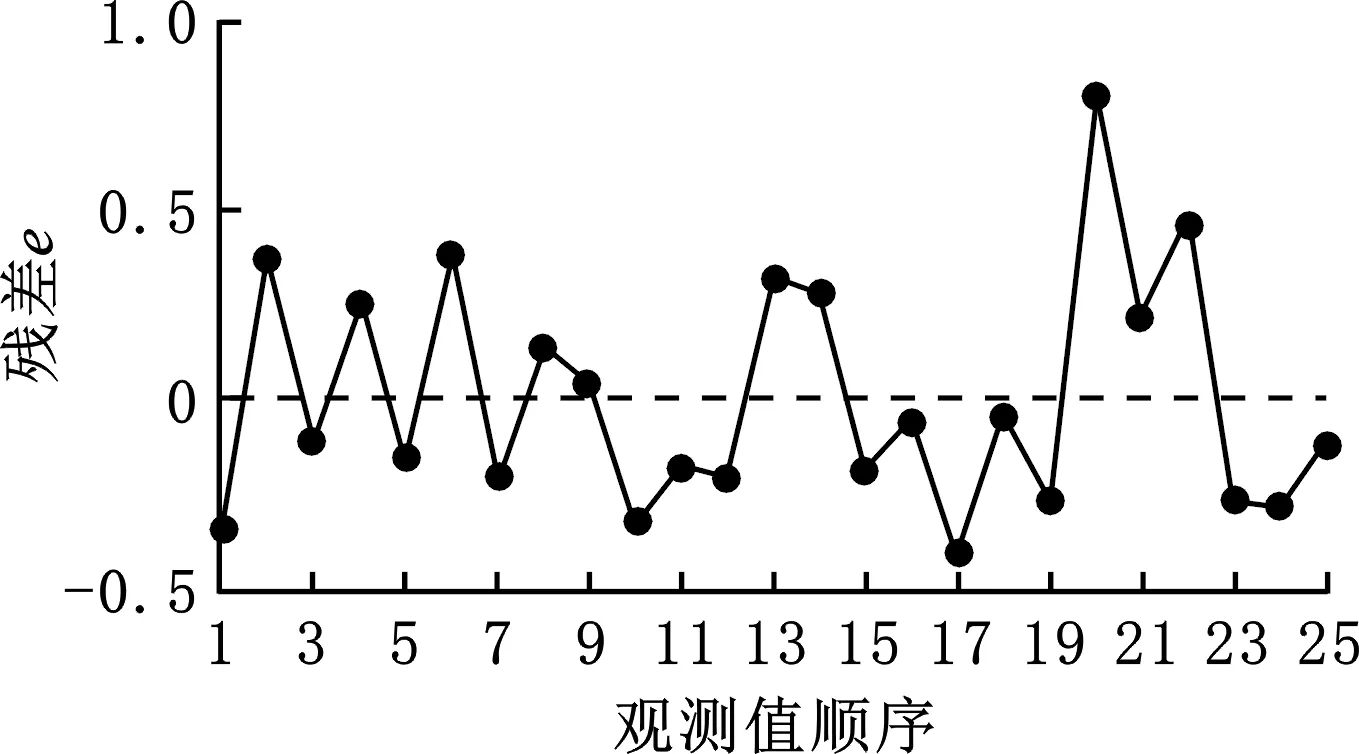
(d)残差与观测值顺序图图8 单位质量平均磁感应强度信噪比残差图Fig.8 Residual map of the SNR of the average magnetic induction intensity per unit mass

2.3 磁场综合性能评估与讨论

通过平均磁感应强度和单位质量平均磁感应强度及显著因素分析可知,截面高度、A截面宽度、B截面宽度3个影响因素的排秩顺序相同,即影响因素的影响效果从大到小的顺序相同,故在设计双峰永磁轨道时,需优先考虑截面高度,其次A截面宽度,再次B截面宽度。从25组工况参数中选择一组最优参数时,需要同时考虑平均磁感应强度和单位质量平均磁感应强度的综合性能。从平均磁感应强度角度观察,排在前5位的是工况20、工况25、工况17、工况24和工况21;从单位质量平均磁感应强度角度观察,排在前5位的是工况1、工况2、工况18、工况14和工况22,两者没有公共交集工况,因此单纯从一个角度评估双峰永磁轨道的磁场性能和选择永磁轨道参数会不合理。将表1中的平均磁感应强度、单位质量平均磁感应强度分别比上每一列的最大值作为磁场相对性能指标,由此得到不同工况平均磁感应强度相对关系、单位质量平均磁感应强度相对关系,如图9和图10所示。

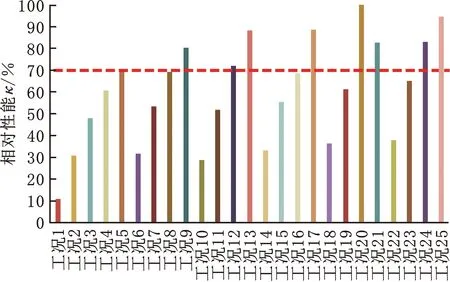
图9 平均磁感应强度对比图Fig.9 Comparison of mean magnetic induction

图10 单位质量平均磁感应强度对比图Fig.10 Comparison of mean magnetic induction per unit mass

取相对性能70%为标准时,出现公共交集,具体为平均磁感应强度的工况5、8、9、12、13、17、20、21、24、25在70%以上;单位质量平均磁感应强度的工况1、2、3、6、7、10、14、18、20、22、23在70%以上。公共交集工况为20,因此根据综合磁场性能确定工况20的尺寸为最佳尺寸。

2.4 优化双峰永磁轨道和实验用双峰永磁轨道磁场性能分析与讨论

实验使用的双峰永磁轨道(A截面宽度为30 mm、B截面宽度为20 mm、截面高度为30 mm、纯铁厚度为10 mm)与仿真得到的优化双峰永磁轨道(A截面宽度为40 mm、B截面宽度为50 mm、截面高度为30 mm、纯铁厚度为6 mm)磁场性能对比关系如图11所示。由图11可以观察到优化得到的最佳结构尺寸Halbach型双峰永磁轨道无论是平均磁感应强度还是单位质量平均磁感应强度都优于实验使用的永磁轨道,故对其优化设计是有效的。

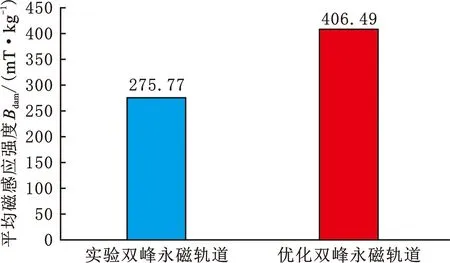
(a)平均磁感应强度

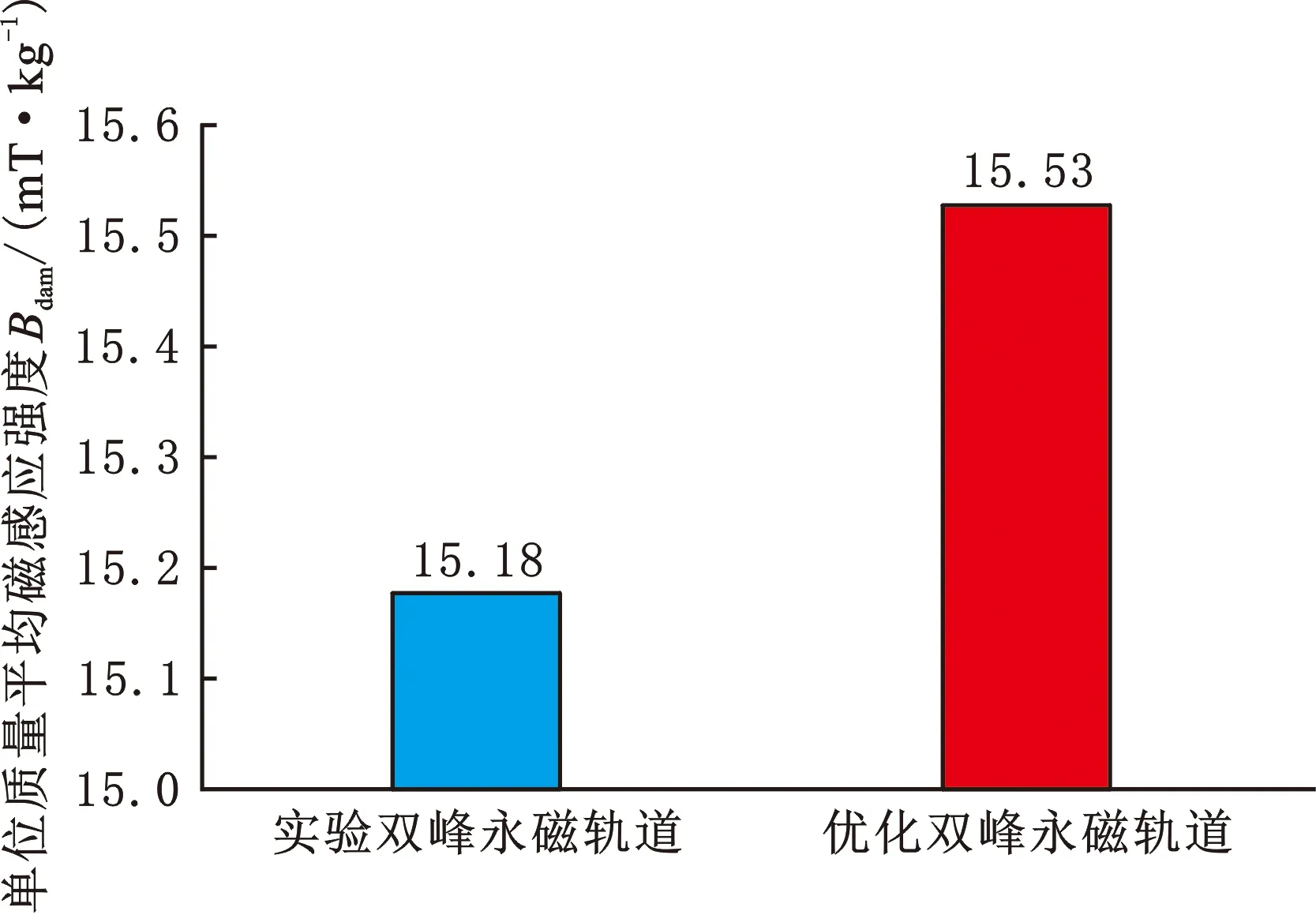
(b)单位质量平均磁感应强度图11 永磁轨道性能对比图Fig.11 The performance comparison diagram of PMR

3 悬浮力特性研究与讨论

3.1 实验装置

列车的稳定悬浮与平稳运行等指标主要由高温超导体与永磁轨道产生的悬浮力决定。本文实验研究场冷条件下高温超导块组合与Halbach型永磁轨道间的悬浮特性,采用的悬浮力实验装置实物和测试工作原理示意图见图12和图13。

图12 悬浮力实验装置Fig.12 Levitation force test device

图13 悬浮力测试装置的结构示意图Fig.13 Schematic diagram of levitation force test device

悬浮力实验装置主要由位移传感器、电机、低温容器(含高温超导块组合)、固定板、压力传感器组成。悬浮力实验测试装置的基本工作原理为:高温超导块组合固定在低温容器中,低温容器固定在电机的端部;位移传感器安装在电机上,通过电机转动得到移动的位移;压力传感器位于永磁轨道的固定板和底板之间;电机带动高温超导块组合上下往复移动,改变永磁轨道与高温超导块组合间的距离,该距离由位移传感器进行测量;压力传感器利用变形反推得到悬浮力,将原始实验数据传给数据采集卡,经过数据处理得到悬浮力。具体实验步骤为:①高温超导块组合接近永磁轨道,设定高温超导块组合和永磁轨道之间的距离即为场冷高度;②将液氮倒入低温容器中,使高温超导块组合在永磁轨道的磁场中冷却(即为场冷情况)进入超导态;③在电机带动下向下移动高温超导块组合,位移传感器测量向下移动的悬浮间隙,压力传感器测量得到高温超导块组合与永磁轨道间的悬浮力,即可完成悬浮力测量实验过程。

实验采用Halbach型双峰永磁轨道,实物见图14,其尺寸和磁化方向如图15所示。单个高温超导块直径为30 mm,厚度为14 mm,而高温超导块组合由10块高温超导块双列排布,即5×2排列方式,示意图见图16。

图14 永磁轨道实物Fig.14 The picture of PMR

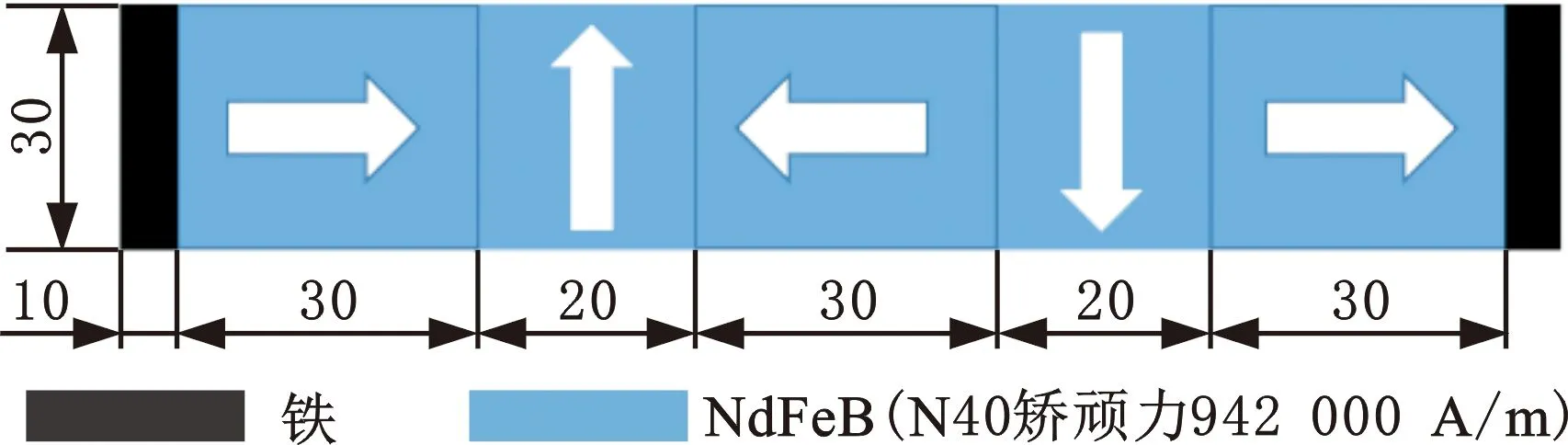
图15 永磁轨道尺寸和磁化方向示意图Fig.15 Diagram of dimension and magnetic direction of PMR

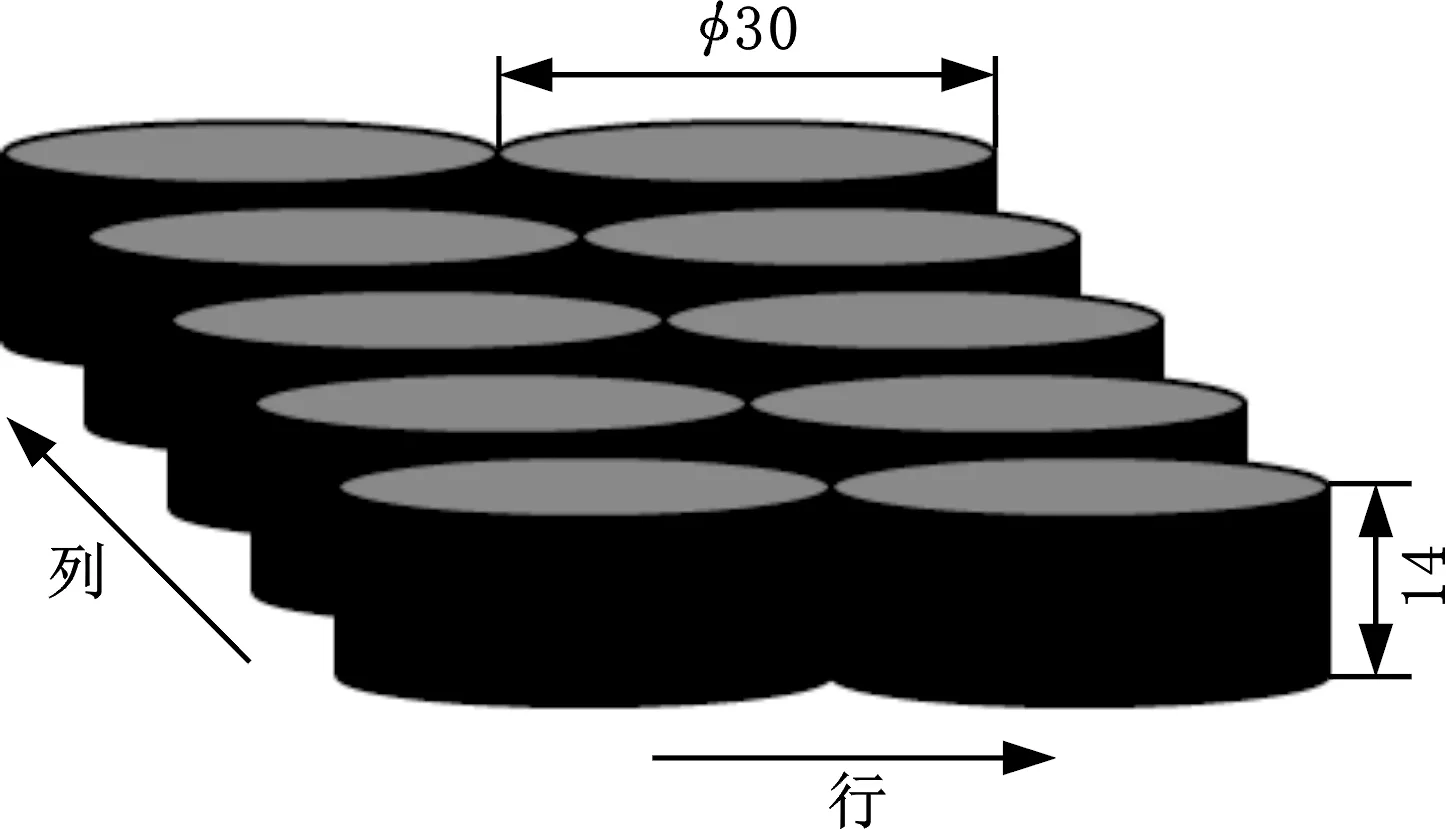
图16 高温超导块组合方式示意图Fig.16 Diagram of high temperature superconductor bulk combination mode

3.2 等效处理方法提出及验证

基于冻结镜像模型[32],高温超导体场冷时在超导体表面和内部同时产生冻结镜像和移动镜像。当高温超导体移动时,冻结镜像保持不动,移动镜像随高温超导体的移动而呈镜向关系移动。冻结镜像等效于高温超导体的捕获磁场,移动镜像等效于高温超导体的抗磁性,因此基于冻结镜像模型提出了等效处理方法,即将高温超导块组合等效处理成具有小的相对磁导率磁体的方法,具体为:利用设定高温超导块组合为小的相对磁导率模拟移动镜像,这时高温超导块组合与永磁轨道产生斥力;利用设定高温超导块组合捕获的磁场模拟冻结镜像,这时高温超导块组合与永磁轨道产生引力;通过斥力和引力矢量求和即可计算高温超导块组合和永磁轨道之间的悬浮力。在该方法中,高温超导块组合捕获磁场的计算依据为场冷高度处悬浮力为0的现象,利用二分算法通过迭代方式得到。将高温超导体磁导率μHTS设为0.01,磁感应强度云图中最大磁感应强度Bmax与最小磁感应强度分别赋值为a和b,计算流程见图17。

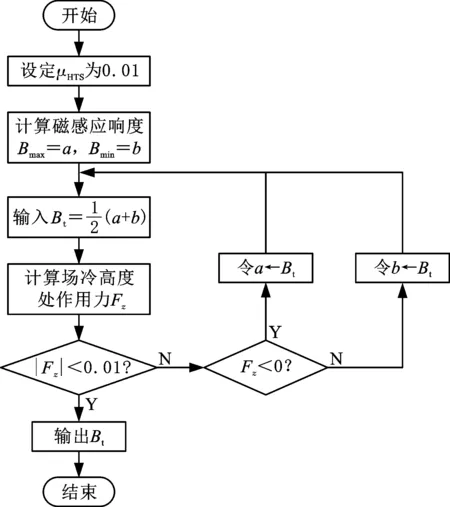
图17 捕获磁场的流程图Fig.17 Flow chart of captured magnetic field

基于等效处理方法计算可以得到高温超导块组合和永磁轨道在场冷高度为22 mm时不同悬浮间隙s下的悬浮力Flev,利用实验装置测得的悬浮力实验数据和基于等效处理方法得到的仿真数据对比关系如图18所示。

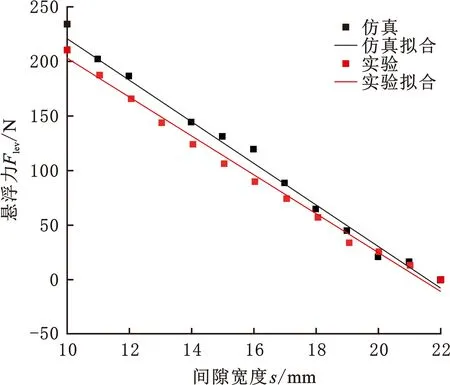
图18 悬浮力实验和仿真对比关系Fig.18 Comparison of experimental and simulated levitation force

由图18可以观察到仿真计算的结果与实验结果趋势相同,悬浮力随着悬浮间隙的减小近似线性增大,仿真与实验结果定量吻合较好,验证了等效处理方法的正确性。因此利用等效处理方法计算了场冷高度为22 mm时优化永磁轨道和5×2排列的高温超导块组合间的悬浮力仿真数据,仿真数据与在相同场冷高度下实验永磁轨道与同样高温超导块组合间的悬浮力实验数据对比如图19所示。

由图19可以观察到,优化永磁轨道悬浮力随悬浮间隙的增大而减小的幅度大于实验永磁轨道悬浮力随悬浮间隙增大而减小的幅度,且在相同的悬浮间隙下能够提供更大的悬浮力,故优化永磁轨道与高温超导块组合配合使用时具有更好的悬浮能力。

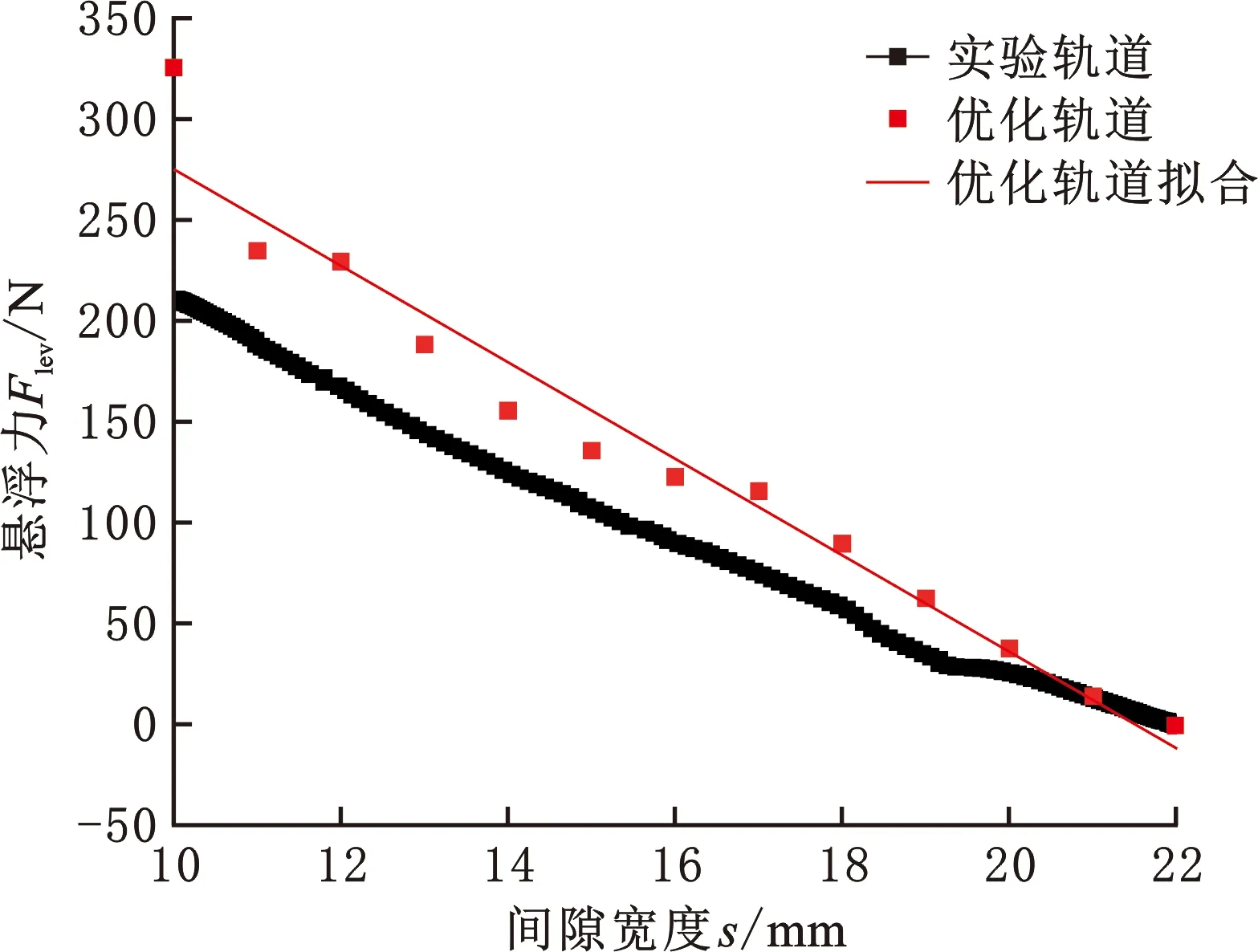
图19 实验轨道与优化轨道悬浮力对比关系Fig.19 Levitation force comparison between experimental PMR and optimized PMR

3.3 不同排列高温超导体的悬浮力仿真与分析

为满足高温超导钉扎磁悬浮列车巨大悬浮力的要求,需改变高温超导块组合排列方式。基于等效处理方法计算不同排列方式的高温超导块组合和优化永磁轨道之间的悬浮力,计算结果如表6所示。由表6可以看出,随着高温超导体行数的增大,最大悬浮力(10 mm处)也随之增大。为了评估悬浮变形能力,根据刚度定义得到悬浮刚度计算公式如下:

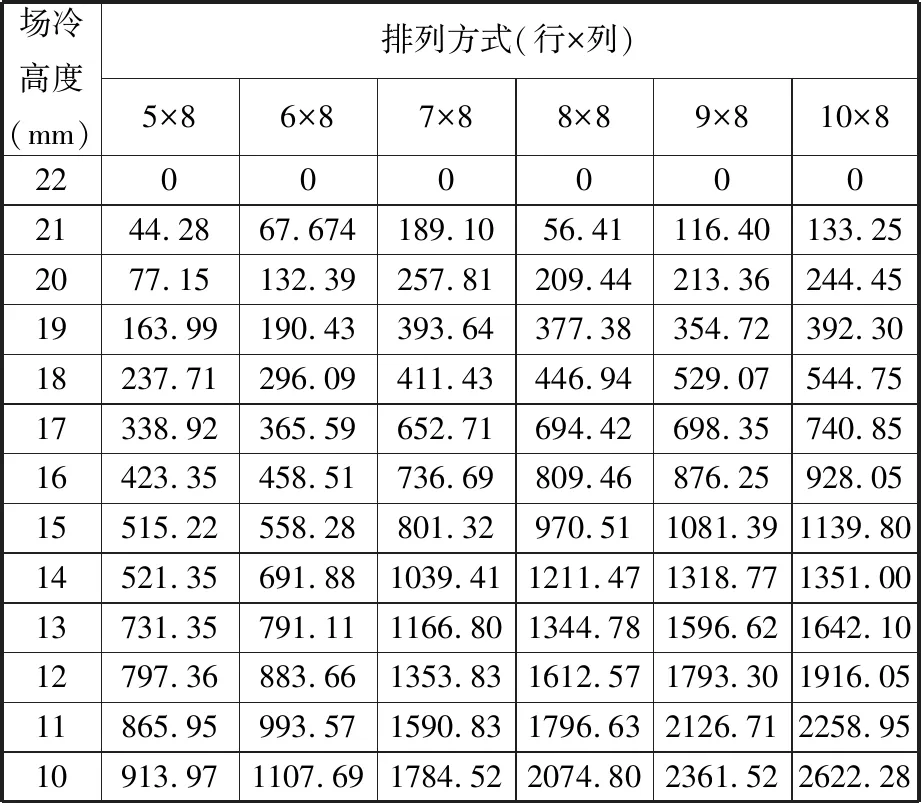
表6 不同排列方式高温超导块组合的悬浮力仿真结果

(3)

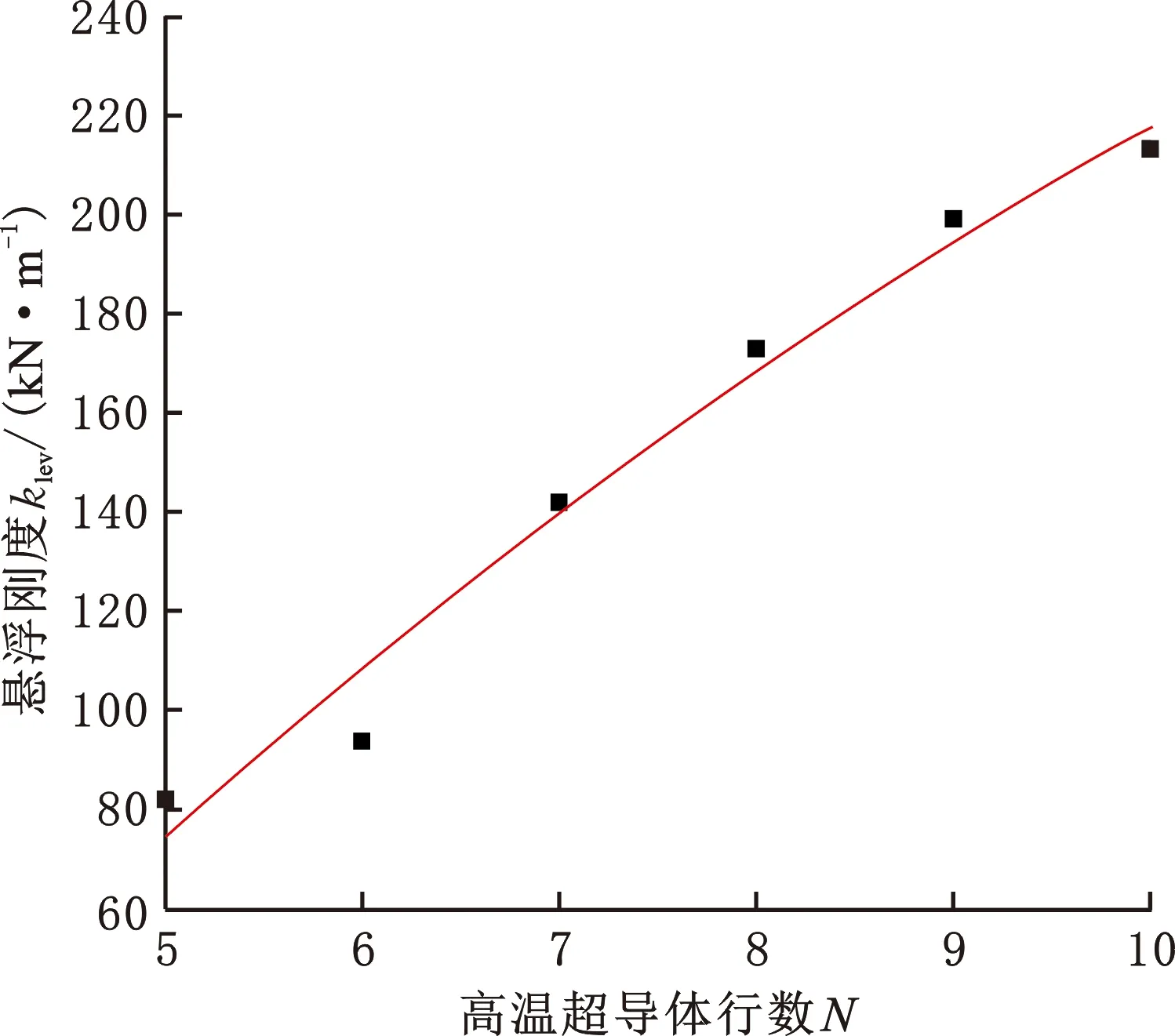
图20 悬浮刚度和排列方式的关系Fig.20 The relationship between levitation stiffness and arrangement

由式(3)可以得到优化永磁轨道和不同行数高温超导块组合间的悬浮刚度,如图20所示。由图20可以看出,随着行数的增大,悬浮刚度迅速增大,因此需要巨大悬浮力时应该布置多行数的高温超导块组合。

4 结论

本文对高温超导钉扎磁悬浮列车中Halbach型双峰永磁轨道的磁场性能进行了研究,基于田口正交方法分析了各结构尺寸对磁场的影响,以综合性能最优为目标找到了各结构的最佳尺寸,通过等效处理方法研究了高温超导体和优化永磁轨道的悬浮特性,得到以下结论:

(1)截面高度对平均磁感应强度和单位质量平均磁感应强度的影响远超A、B截面宽度的影响,纯铁厚度为非显著因素。A截面宽度为40 mm、B截面宽度为50 mm、截面高度为30 mm、纯铁厚度为6 mm时双峰永磁轨道的综合磁场性能最佳。

(2)基于冻结镜像模型提出了等效处理方法,通过实验数据验证了等效处理方法的正确性,利用该方法可计算高温超导块组合和永磁轨道的悬浮力。

(3)优化永磁轨道场冷高度为10 mm处悬浮力是实验永磁轨道场冷高度为10 mm处悬浮力的1.5倍,表明优化永磁轨道悬浮特性明显优于实验永磁轨道,且悬浮刚度随高温超导块行数的增加迅速增大。