精确预测近平面应变载荷下各向异性行为的屈服准则参数识别策略
都 凯 任彦强 侯 勇 李小强 陈帅峰 孙 亮 左晓姣 袁晓光
1.沈阳工业大学材料科学与工程学院,沈阳,110870 2.首尔国立大学材料科学与工程学院,首尔,08826 3.北京航空航天大学机械工程及自动化学院,北京,1001914.中国科学院金属研究所师昌绪先进材料创新中心,沈阳,110016
0 引言
在现代汽车工业中,随着燃油经济性和碰撞安全性要求的不断提高,轻质高强板材在主机厂得到了广泛的应用。然而,这些商用汽车板材经过复杂的热机械加工后具有明显的各向异性,对板材成形性能有显著的影响[1]。为此,精确表征材料的塑性各向异性行为对冲压过程中避免出现开裂、颈缩、起皱和回弹等缺陷具有重要的理论意义与工程价值[2-3]。
过去几十年,许多能够描述金属板材塑性各向异性行为的材料模型得到研究和发展。其中,Hill48二次各向异性屈服准则[4]最为著名,它数学形式简单,校准成本低廉,直到现在仍然在工业界和学术界广泛应用。为了精确描述铝合金的各向异性行为,BARLAT等[5-6]在Hosford各向同性屈服准则基础上提出了一系列非二次形式的各向异性屈服准则。受到“等效各向同性”概念的启发,BARLAT等[7]又进一步建立了著名的Yld2000-2d屈服准则,并开创性地使用等双轴拉伸塑性应变比识别了屈服准则的各向异性系数,为丰富校准策略作出了重要贡献。基于Hershey各向同性屈服准则,BANABIC等[8]通过引入权重因子开发了BBC2003屈服准则,这一屈服准则的改进版本被称之为BBC2005[9]。然而,这些屈服准则一般无法描述筒形件深拉延试验中观察到的六凸耳或八凸耳现象。因此,为了继续提高屈服准则的灵活性,研究人员相继开发出多种能够进一步精确反映板材面内各向异性的先进屈服准则,如Yld2004-18p[10]、BBC2008[11]、Yld2011-27p[12]、Yoshida2013[13]和Poly4*Hosford[14]等。
通常情况下,上述屈服准则的指数被认为是一个固定的常数,主要取决于材料的晶体学结构。事实上,恒定指数应该理解为一种指导原则,并不具备物理基础,即没有考虑到指数对屈服轨迹曲率的潜在调节作用。PILTHAMMAR等[15]指出,基于瑞典沃尔沃汽车公司对大量材料反向建模的实际经验,如果允许指数的取值为正数而不是正整数,则BBC2005屈服准则能够更精确地描述材料的变形行为。宝马集团和蒂森克虏伯欧洲钢铁公司的研究人员开发了一系列小型冲压模具,并将拉延深度的预测精度作为指数校准标准[16]。然而,实验过程中的润滑与摩擦行为会显著影响成形结果,导致通过逆向识别方法标定指数有可能无法准确反映材料的本质成形属性[17]。考虑到近平面应变载荷与屈服面上所有应力状态中主应力最高的极值点相关,并且以近平面应变载荷结尾的应变路径变化在金属板材成形过程中最为常见[18],因此,对于建模精度具有特殊要求的车身覆盖件(如门内板、翼子板和轮罩等)仿真分析工作,进一步引入近平面应变数据校准屈服准则的指数能够全面提高材料各向异性屈服行为的描述能力。HOU等[19-20]通过十字形双轴拉伸试验测量的近平面应变数据标定了CQI2022和mKB93屈服准则的指数与形状控制项,显著提高了先进高强钢与铝合金板材塑性各向异性行为的预测精度。然而,目前大多数工业级实验室中,一台标准单轴拉伸试验机以及一台能够开展液压胀形和成形极限曲线测定的板成形万能试验机是当前的标准配置,几乎很少配备双轴拉伸试验装置(例如宝马集团铁西工厂TWA材料分析测试中心)。因此,为了获得可靠的双轴力学性能并将其用于校准屈服准则的指数和材料参数,一方面可参考AN等[21]或LOU等[22]提出的方法通过单轴拉伸试验机测量近平面应变状态下主应力方向数据,另一方面可通过液压胀形试验获取等双轴拉伸力学性能和大塑性应变条件下的硬化曲线。对于液压胀形试验不适合确定双轴各向异性系数的问题,可通过MIN等[23]提出的方法对液压胀形测量数据进行修正。
本文提出一种基于单轴拉伸、等双轴拉伸和近平面应变力学性能标定先进各向异性屈服准则指数和材料参数的高效率校准策略,通过4种商用汽车板材(MP980、SPCE、5182-O和A6XXX-T4)定量评估应用本文提出的新校准策略的BBC2008屈服准则和其他几种工业界广泛使用以及与BBC2008灵活性相当的材料模型(包括Hill48、Barlat89、Yld2004-18p、Yld2011-27p、Yoshida2013和Poly4*Hosford)对法平面屈服轨迹、对角线平面剪切屈服轨迹、等双轴和单轴拉伸屈服应力与塑性应变比(r值)的描述能力。
1 试验材料与方法
1.1 试验材料
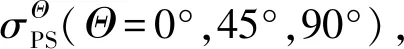

表1 MP980、SPCE、5182-O和A6XXX-T4的力学性能
1.2 参数识别策略
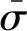
ωs-i||M(i)+N(i)|2k+|M(i)-N(i)|2k|}
(1)
ω=(3/2)1/s
(2)
(3)
(4)
(5)
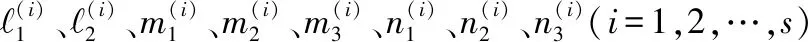
沿轧制方向呈不同角度的单轴和等双轴拉伸屈服应力与r值在COMSA等[11]的研究中提供了详细的理论推导过程。对于近平面应变加载条件,根据应力坐标变换公式,沿0°、45°和90°方向的近平面应变屈服应力对应的柯西应力张量的分量可分别表示为
(6)
(7)
(8)
式中,Ψ0°、Ψ45°和Ψ90°分别为与轧制方向成0°、45°和90°的平面应变拉伸试验中横向与纵向应力的比值。
在关联流动法则的框架下,考虑到平面应变状态无横向应变的事实,即
(9)
(10)
(11)
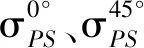
(12)
{θ1,θ2,…,θ7}={0°,15°,…,90°}
{Θ1,Θ2,Θ3}={0°,45°,90°}
式中,量符号的上标“cal”与下标“exp”分别表示理论预测值与试验测量值。
其他几种屈服准则(Hill48、Barlat89、Yld2004-18p、Yld2011-27p、Yoshida2013和Poly4*Hosford)识别材料参数所需的力学性能被列于表2,“{}”中的数字表示校准屈服准则所需力学性能的数量。在全部考察的屈服准则中,Hill48和Barlat89的材料参数可由应力各向异性数据或r值各向异性数据分别解析计算[28-29],本文选取工程领域经常使用的r值各向异性数据求解方法。Yld2004-18p和Yoshida2013的标定策略与传统BBC2008屈服准则的校准方法一致,即通过单轴和等双轴拉伸屈服应力与r值进行标定。Yld2011-27p的校准程序可参考图1,唯一不同之处在于近平面应变数据参与到了材料参数的识别当中,指数仍然根据不同的晶体学结构进行选择。Poly4*Hosford为解析屈服准则,不需要通过任何插值和优化技术校准材料参数。

表2 识别不同屈服准则的材料参数所需的力学性能
2 结果和分析
本节通过比较理论预测与试验测量的法平面屈服轨迹、对角线平面剪切屈服轨迹以及等双轴和单轴屈服应力与r值,定量评估应用新参数识别策略的BBC2008屈服准则与其他几种屈服准则(包括Hill48、Barlat89、Yld2004-18p、Yld2011-27p、Yoshida2013和Poly4*Hosford)对MP980、SPCE、5182-O和A6XXX-T4各向异性屈服行为的描述能力。
2.1 校准结果
表3~表9分别总结了基于Hill48、Barlat89、Yld2004-18p、Yld2011-27p、Yoshida2013、Poly4*Hosford和BBC2008屈服准则的材料参数标定结果,其中,包含指数形式的非二次屈服准则(如Barlat89、Yld2004-18p、Yld2011-27p和Poly4*Hosford)仅考虑了经常在体心立方和面心立方材料中推荐使用的整数指数M=a=m=n=6和M=a=m=8、n=10。
2.2 不同屈服准则的描述精度评估
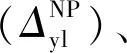
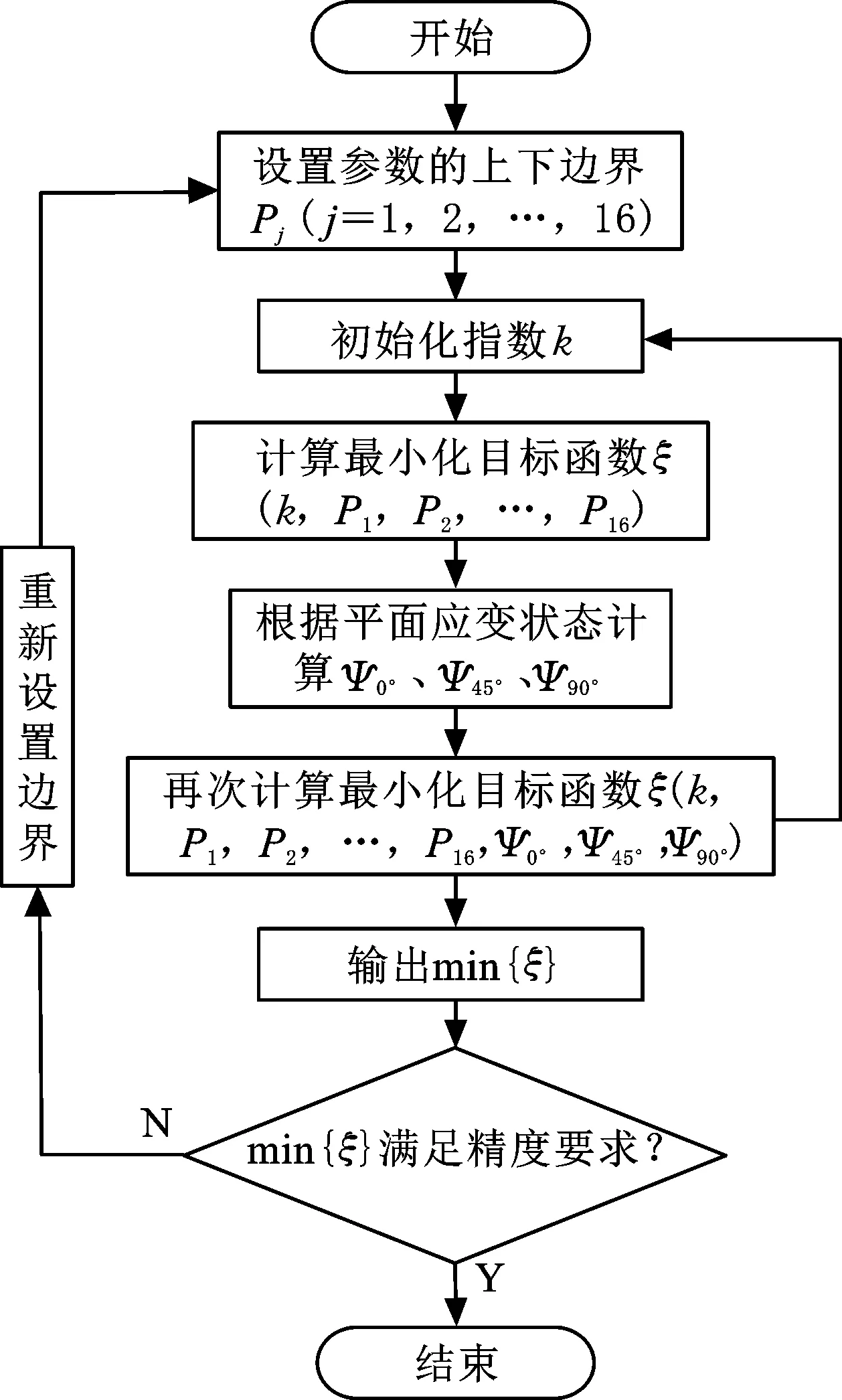
图1 应用新参数识别策略校准BBC2008屈服准则指数和材料参数的流程图Fig.1 Flow chart for calibrating the exponent and material parameters of the BBC2008 yield criterion using a new parameter identification strategy

表3 Hill48屈服准则各向异性系数F、G、H、N的计算结果

表4 Barlat89屈服准则各向异性系数a、c、h、p与指数M的计算结果
(13)
(14)
(15)
α,β=x,y

表5 Yld2004-18p屈服准则各向异性系数 (i1=1,2,3,6;j1=1,2,3,6)与指数a的计算结果

表6 Yld2011-27p屈服准则各向异性系数ci2j2‴ (i2=1,2,3,6;j2=1,2,3,6)与指数m的计算结果
式中,“NP”、“DP”分别表示法平面和对角线平面;下标“yl”表示屈服轨迹;“σαβ(m)”表示第m个实验屈服应力的应力分量;“M”表示测试加载路径的数量,在本文中,MNP=9、MDP=3或5。
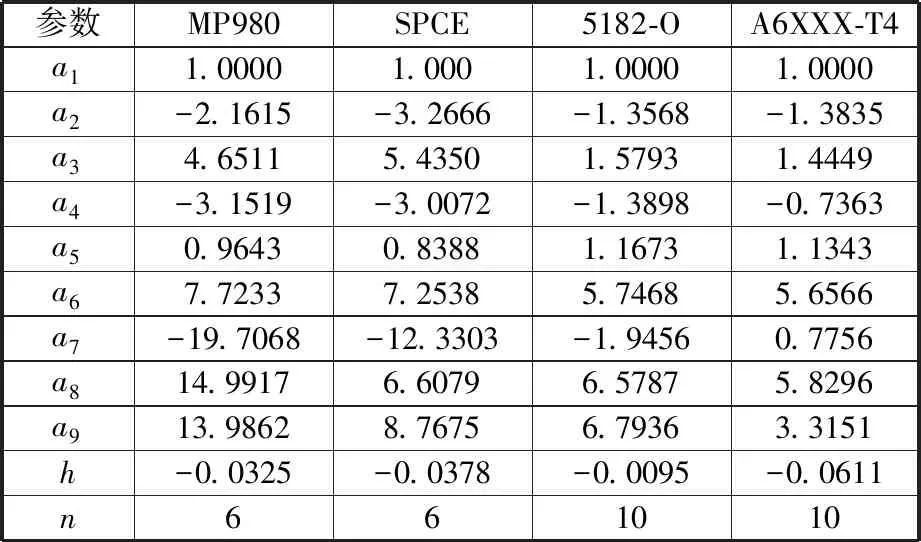
表8 Poly4*Hosford屈服准则各向异性系数ai4(i4=1,2,…,9)、过程参数h和指数n的计算结果

表9 BBC2008屈服准则各向异性系数和指数k的计算结果(s=2)
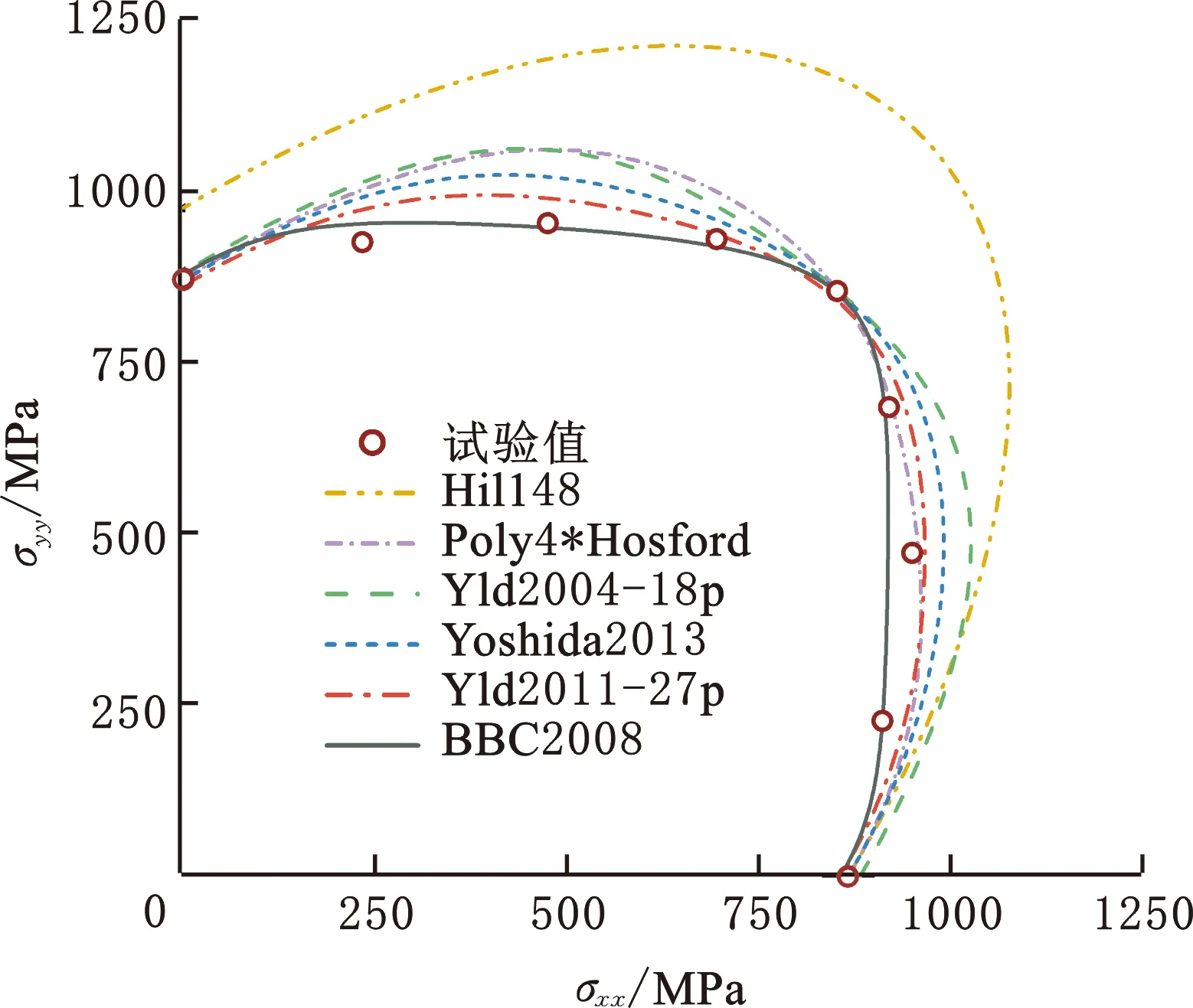
(a)MP980
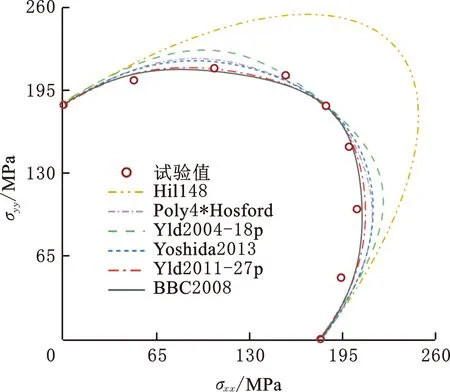
(b)SPCE
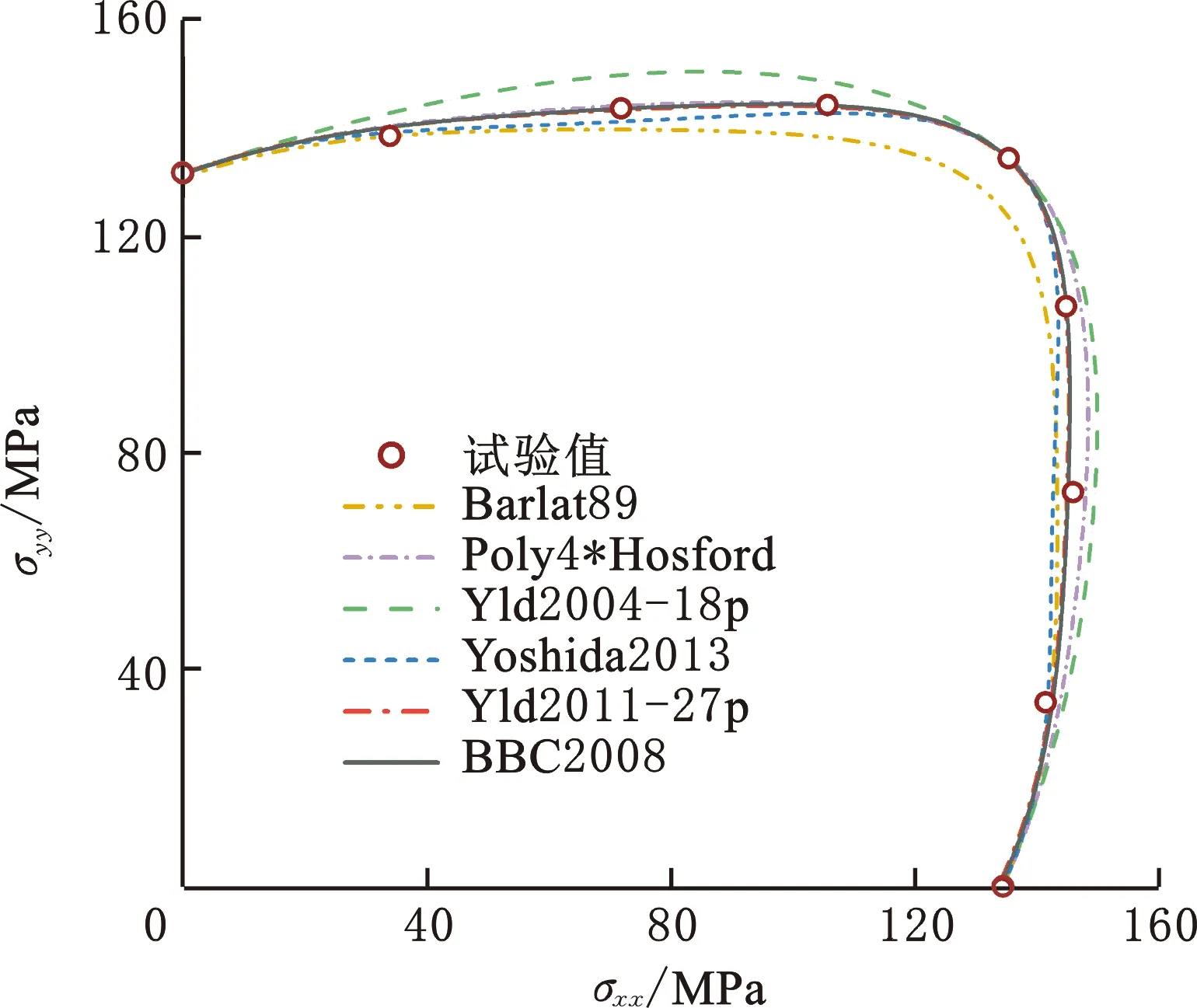
(c)5182-O
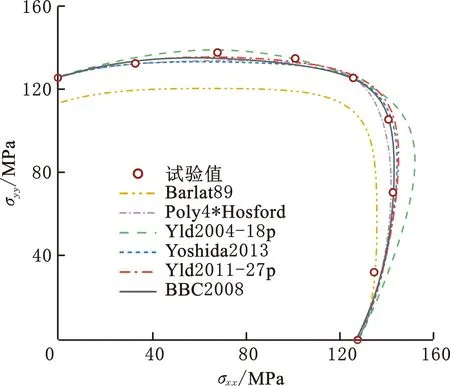
(d)A6XXX-T4图2 不同屈服准则预测的法平面屈服轨迹Fig.2 Normal plane yield loci predicted by different yield criteria

(a)MP980 (b)SPCE
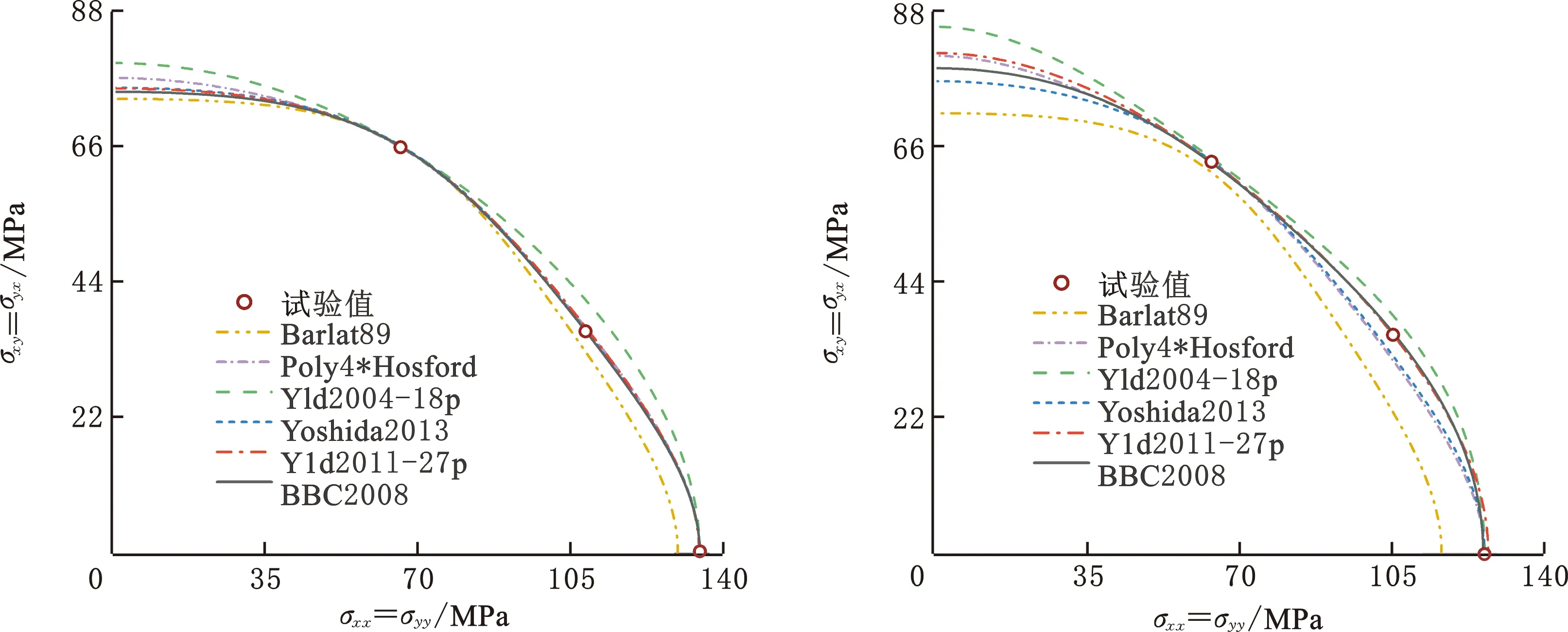
(c)5182-O (d)A6XXX-T4图3 不同屈服准则预测的对角线平面剪切屈服轨迹Fig.3 Diagonal plane shear yield loci predicted by different yield criteria
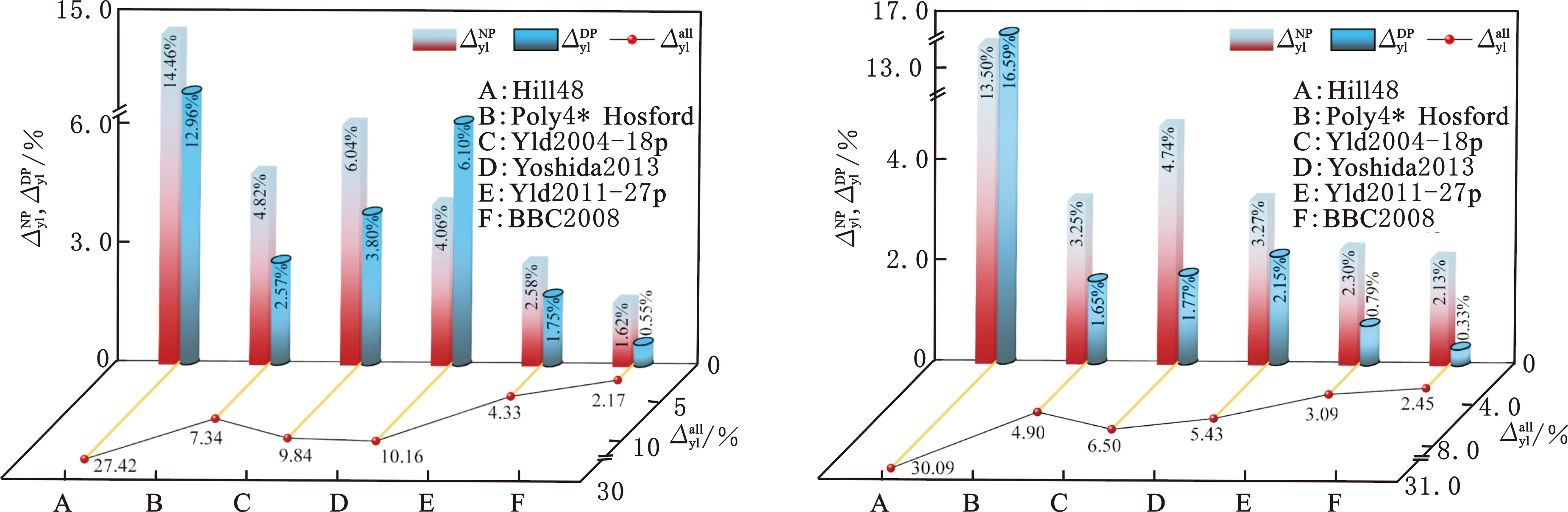
(a)MP980 (b)SPCE
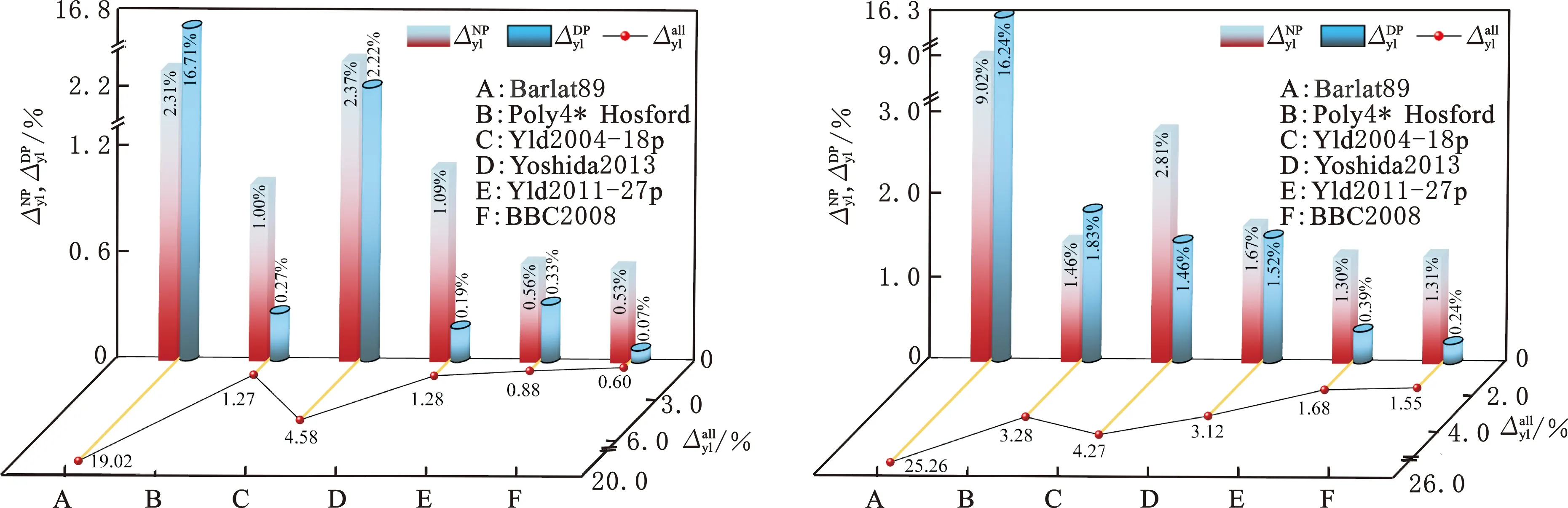
(c)5182-O (d)A6XXX-T4图4 不同屈服准则计算的法平面误差对角线平面误差和累积误差Fig.4 Normal plane plane cumulative calculated by different yield criteria
图5和图6分别显示了不同屈服准则预测的等双轴拉伸应力状态下MP980、SPCE、5182-O和A6XXX-T4的σb和rb,并与试验数据进行比较。可以看出,Hill48和Barlat89的预测精度最不理想,因为这两个屈服准则并未使用等双轴拉伸数据进行校准。然而,尽管Yld2004-18p和Yld2011-27p使用了σb和rb,但在预测σb方面却显示出一定的预测误差,如图5所示。这可以归因于校准使用的试验数据数量与屈服准则所能容纳的材料参数数量不匹配,导致误差的择优分配要以牺牲σb的预测精度为代价。因此,在不附加额外数学约束的前提下,如改变σb在最小化目标函数中的权重,Yld2004-18p和Yld2011-27p只能提供当前全部校准试验数据的全局最优解。此外,Poly4*Hosford在参数校准过程中使用了rb,并且校准数据与材料参数的数量保持了一致。但是对于rb还是显示出相当大的计算偏差,如图6所示。这可以归因于rb仅为过程参数h的校准提供判据,并未直接参与到计算中。因此能够得出结论:高阶模型对减小rb的预测误差无帮助,仅在等双轴拉伸力学性能被使用并且直接参与到材料参数的校准当中才能获得精确的预测结果。

(a)MP980 (b)SPCE
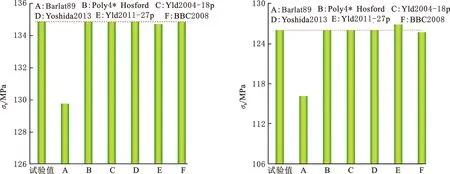
(c)5182-O (d)A6XXX-T4图5 不同屈服准则预测的σbFig.5 σb predicted by different yield criteria
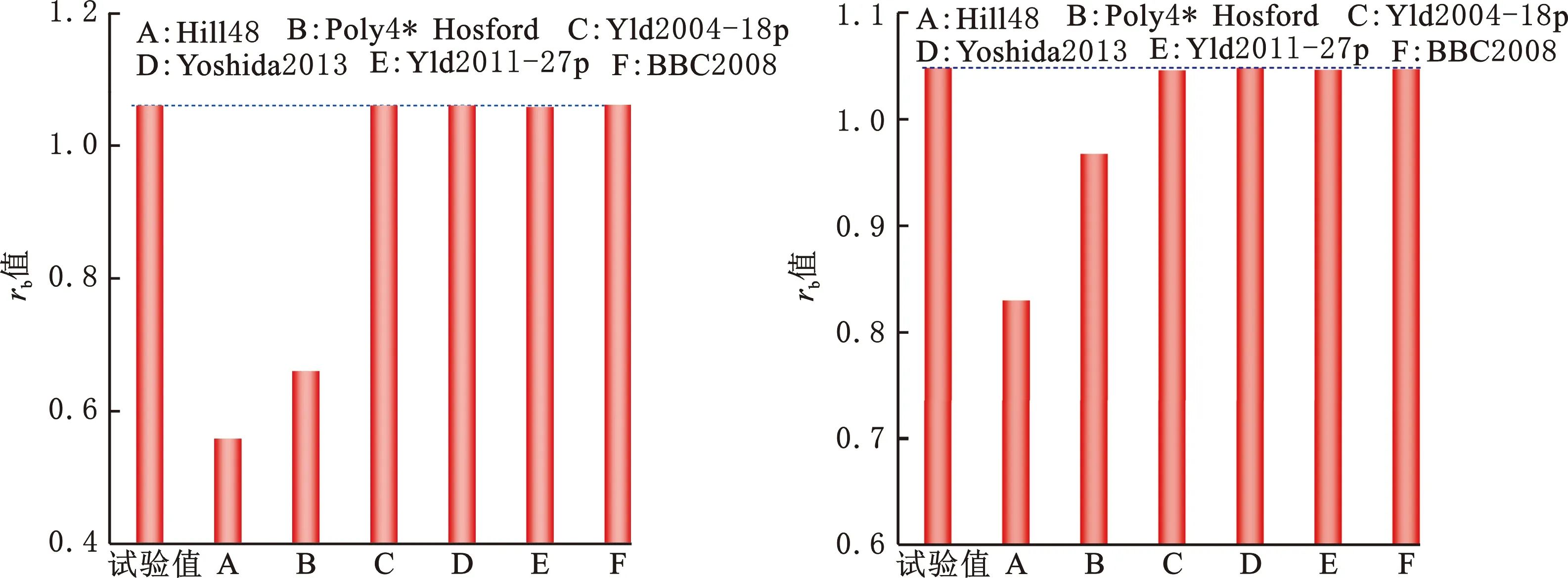
(a)MP980 (b)SPCE
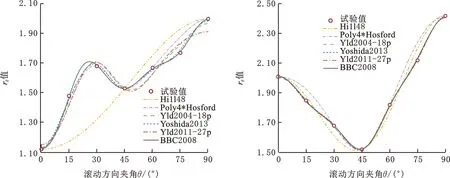
图7和图8分别比较了不同屈服准则预测的随加载角度变化的单轴拉伸屈服应力σθ和r值。能够观察到,不同屈服准则预测的σθ波动性要强于rθ的波动性。为了进一步定量评估不同屈服准则对σθ和rθ的预测精度,采用DU等[32]提出的分析指标计算单轴拉伸屈服应力误差ΔU与r值误差Δr:
(16)
(17)
式(16)、式(17)中分别增加了15°、30°、45°、60°和75°方向的权重,目的是反映105°、120°、135°、150°和165°方向的贡献。
图9显示了采用不同屈服准则计算的ΔU与Δr。能够观察到,Yld2004-18p、Yoshida2013、Yld2011-27p和BBC2008在描述不同材料的单轴拉伸各向异性屈服和塑性流动时,表现出更高水平的预测精度,这是因为上述4种屈服准则均使用了以15°为增量的单轴拉伸力学性能校准材料参数(表2),因此,对σθ和rθ的预测精度显著高于使用力学性能数量较少的Hill48、Barlat89和Poly4*Hosford的预测精度。此外,Poly4*Hosford与Hill48和Barlat89相比,虽然额外增加了r30°和r60°校准屈服准则的材料参数,但对SPCE和A6XXX-T4的rθ预测精度并未见提高,见图9b和图9d。这可能是因为SPCE和A6XXX-T4的rθ各向异性数据表现出先下降后上升的有序变化,而不像MP980和5182-O,必须要施加更多的面内r值约束来捕捉跌宕起伏的复杂变化趋势。因此,仍然可以将使用更多单轴力学性能校准材料参数但预测精度未得到改善的根本原因归结为对材料特性的高度依赖。
上述定量分析结果表明,与众多先进的屈服准则相比,通过本文方法校准的BBC2008屈服准则能够更加精确地描述几种商用汽车板材的各向异性屈服行为,如图4和图9所示,这表明所开发的参数识别策略的有效性和先进性。此外,应该强调的是,本文方法具有良好的可移植性,不仅限于BBC2008屈服准则。同时,由于本文提出的参数识别策略只需通过当前工业级实验室配置的标准测试设备即可实现,因此该方法具备良好的工业应用前景。

(a)MP980 (b)SPCE

(c)5182-O (d)A6XXX-T4图7 不同屈服准则预测的σθFig.7 σθ predicted by different yield criteria
(a)MP980 (b)SPCE
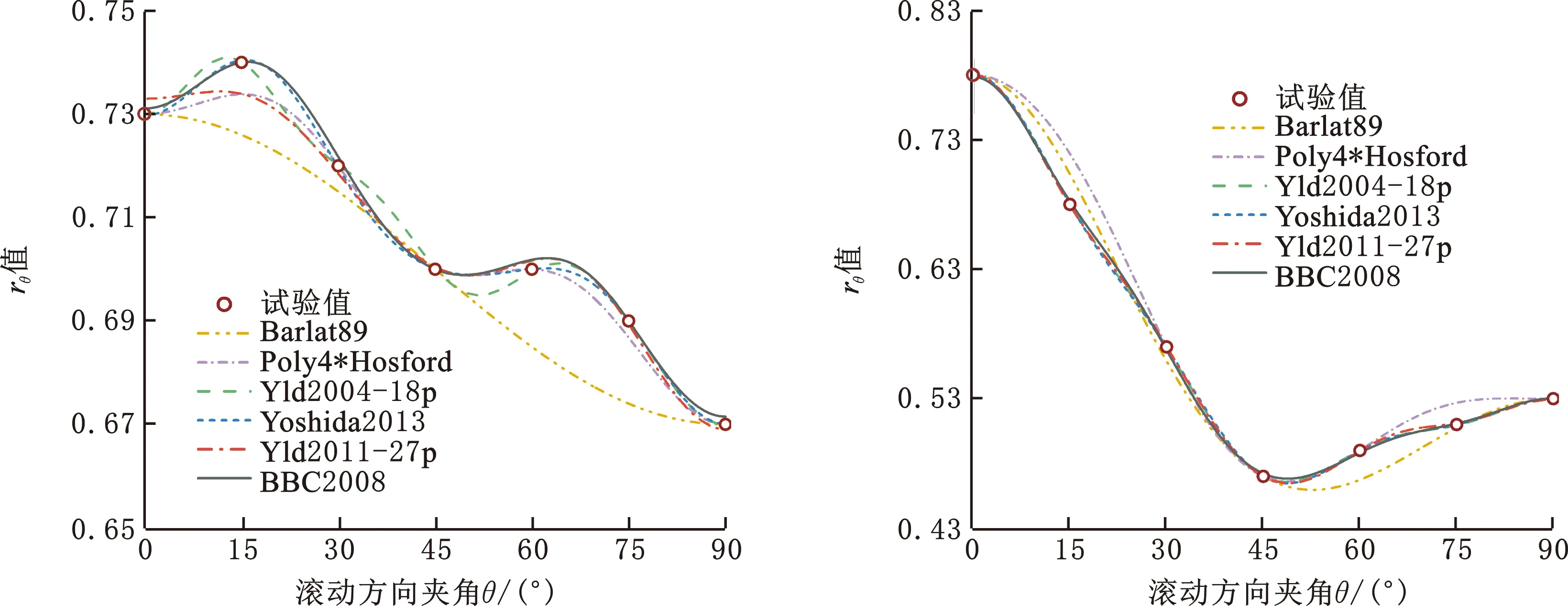
(c)5182-O (d)A6XXX-T4图8 不同屈服准则预测的rθFig.8 rθ predicted by different yield criteria

(a)MP980 (b)SPCE

(c)5182-O (d)A6XXX-T4图9 不同屈服准则下的单轴屈服应力误差ΔU和rθ 误差ΔrFig.9 Uniaxial yield stress error ΔU and rθ errors Δr for different yield criteria
3 结论
基于4种商用汽车板材(MP980、SPCE、5182-O和A6XXX-T4)系统性地评估了几种关联屈服准则对材料塑性各向异性方面的描述能力,提出并检验了一种适用于当前工业级实验室检测水平的先进各向异性屈服准则参数识别策略,可以得到如下结论:
(1)在单轴和等双轴拉伸力学性能基础上,进一步引入近平面应变数据校准屈服准则的指数,能够显著提高复杂载荷下各向异性屈服行为的描述能力。
(2)在校准屈服准则所使用的全部力学性能数据中,应特别重视45°方向近平面应变屈服应力对对角线平面剪切屈服轨迹的约束作用。
(3)在预测单轴和等双轴拉伸力学性能时,相应的试验性采样点如果没有直接参与到屈服准则的参数识别当中,即使使用灵活性更强的高阶模型也无助于减小预测误差。
(4)在使用相同试验数据校准屈服准则材料参数的前提下,释放指数的潜在调节能力比增加材料参数的数量更加重要。
(5)与其他各向异性屈服准则相比,施加了新参数识别策略的BBC2008屈服准则可以为MP980、SPCE、5182-O和A6XXX-T4的塑性各向异性行为提供最佳的预测精度。

