基于概率相关慢特征分析的高速列车牵引系统故障检测

张瑞婷, 翟 双, 程 超, 曹文松

(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)

0 引 言

高速列车因其快速舒适的优点,逐渐成为人们出行的首选工具,列车的安全也与人们的生命财产安全关联愈发紧密。虽然列车事故发生概率较低,但是因其速度快、乘客多,一旦发生事故往往会造成巨大损失。而牵引系统作为高速列车的核心,如何准确、快速地检测出其故障显得尤为重要[1]。

故障检测技术依照传统分类方法可分为三类:基于模型分析方法[2-6]、基于信号分析方法[7-8]和基于数据驱动方法[9-12]。近年来,基于数据驱动方法尤其是多变量统计方法因其易于实现被广泛应用在高速列车牵引系统的故障检测方法中[9-12]。

主元分析方法(Principal Component Analysis, PCA)是多元统计方法中最经典的方法。文献[13]在PCA和核方法的基础上提出一种改进的深度主元分析方法(Deep Principal Component Analysis, DePCA),在深度学习基础上设计一种分层统计模型来提取多层数据特征。PCA的应用要求数据满足高斯分布和线性相关,显然实际列车运行的情况下很难满足。

为了解决非高斯问题,引入独立主元分析方法(Independent Component Analysis, ICA),ICA设计的初衷是为了解决经典鸡尾酒问题(盲源分离问题)[14]。文献[15]将ICA和PCA相结合,可以同时提取多变量过程的高斯信号和非高斯信号。ICA方法通过尽量去除数据间的相关性解决非高斯问题,但同时也使其很难达到最优效果。

考虑到故障信息有明显的时间相关性,慢特征分析方法(Slow Feature Analysis, SFA)被引入故障检测领域[16]。文献[16]将SFA应用于高速列车齿轮系统,考虑早期故障对齿轮系统的影响,提出基于海灵格距离的解决方案。

文中基于对多元统计方法和高速列车牵引系统的研究,设计一种基于概率相关的改进SFA方法(Probability Related Slow Feature Analysis, PRSFA),并在仿真平台加以验证,结果表明,PRSFA有效提高了故障检测性能。主要工作如下:

1)提出SFA与KLD结合的方法,降维筛选出时间序列的慢速特征,利用故障信息的时间相关性,计算离线与在线慢特征的概率分布距离实现故障检测。

2)将文中所提方法应用于中南大学的列车牵引控制模拟仿真系统,与已有算法进行对比,结果表明,改进的SFA算法具有更低的误报率和漏报率,有效提高了故障检测性能。

1 高速列车牵引系统介绍

考虑CRH2型高速列车,其电气原理如图1所示。

图1 CRH2型牵引系统电气原理图

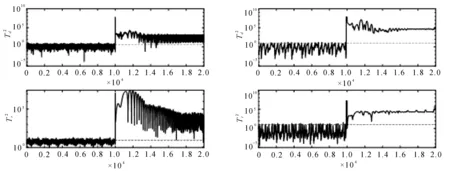
(a) SFA (b) PRSFA

CRH2型高速列车牵引系统主要由牵引控制器、牵引电机、三电平逆变器、牵引变压器、滤波器等组成,采用的控制策略为空间矢量脉宽调制,在设定了给定的牵引速度后,控制单元可以通过基于空间矢量脉宽调制策略调整三电平逆变器的门控制信号来控制牵引系统[17]。

CRH2型高速列车的牵引系统安装了如速度传感器、电压传感器、电流传感器等不同类型传感器,用于监控列车运行状态。根据故障发生位置,一般将高速列车的牵引系统故障分为电机故障、传感器故障、变流器故障、控制单元故障等。监控单元通过比较在线采样和预先设定的阈值来监测故障,然后激活自动保护系统,现实中,由于存在误报和漏报的可能,监测单元可能无法正确监测故障,仍需要大量人力沿线排查。因此,尽可能降低误报率和漏报率尤为重要。

2 概率相关慢特征分析方法

2.1 Kullback-Leibler散度

Kullback-Leibler 散度[18]用于测量两个概率分布之间的差异,文中使用KLD度量慢特征矩阵概率分布之间的距离。对于关于随机变量x的两个连续概率分布函数g0(x)和g1(x),它们的KL散度通常表述为

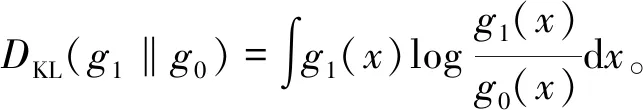
(1)

DKL(g1‖g0)越小,代表概率分布函数g0(x)和g1(x)越相似,DKL(g1‖g0)≥0,当且仅当g0(x)=g1(x)时,DKL(g1‖g0)=0。

由于KL散度是一个非对称的度量,从g0(x)到g1(x)的KLD不一定与从g1(x)到g0(x)的KLD相同,不适用于距离测量,实际应用中我们采用其改进的对称形式

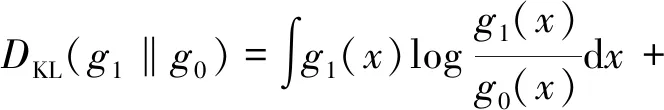
(2)

当概率密度函数g0(x)和g1(x)服从正态分布,即g0(x)～N(μ0,σ0),g1(x)～N(μ1,σ1),DKL(g1‖g0)可计算为

DKL(g1‖g0)=

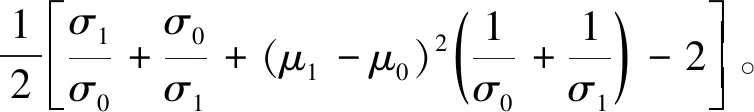
(3)

在数据非高斯的情况下,σ1和μ1可由滑窗计算为

(4)

2.2 慢特征分析方法

慢特征算法的核心思想是从变化速度较快的时间序列信号中提取出变化最为缓慢的特征,也是一种特征提取和降维的方法。

对于牵引系统中传感器输入数据X(t),将其归一化得到数据矩阵为

x={x1,…,xm},x∈RN×m,

(5)

式中:N----样本数;

m----变量数。

对x的协方差矩阵进行SVD分解,

〈xxT〉t=UΛUT,

(6)

式中:〈·〉t----在时间序列的均值。

数据矩阵x的白化过程可以表示为

(7)

白化过程的目的在于消除数据之间的相关性,根据

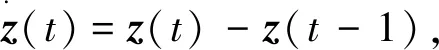
(8)

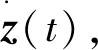
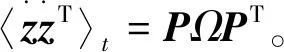
(9)

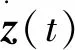
s=xW,

(10)

其中W=QpT,同时,z的协方差矩阵可以计算为

〈zzT〉t==pΣpT,

(11)

式中:Σ----特征值矩阵,Σ={ζ1,…,ζm}。

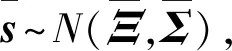
一般认为慢特征s可分为主元部分sr和残差部分sd, 其中,sr主要包含牵引系统状态变化的主要信息,而sd包含较多噪声信息。

2.3 概率相关慢特征分析方法

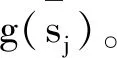
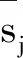
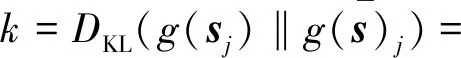
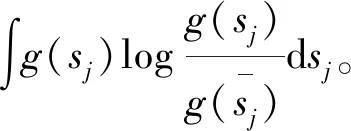
(12)

当s为非高斯,其核函数计算为

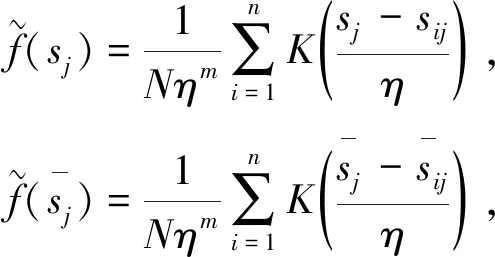
(13)

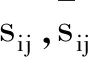
K(·)----核函数。

η可为

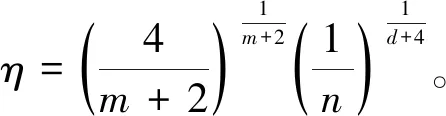
(14)

由此,根据慢特征的概率密度分布,式(12)可以进一步写为

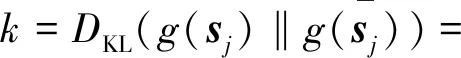
(15)

2.4 故障检测

基于PRSFA,新的T2统计量为

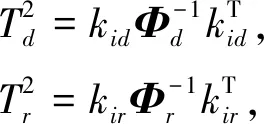
(16)

式中:kir,kid----分别表示训练数据的主元部分sr和残差部分sd的KL散度,kir∈RM,kid∈RMe;

Φr,Φd----分别表示kir和kid的协方差矩阵;

M,Me----分别表示主元部分和残差部分的样本数量,m=M+Me。

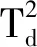
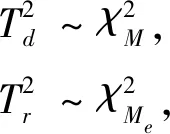
(17)

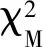
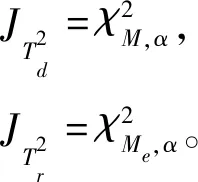
(18)

故障判别如下:

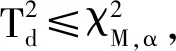
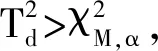
3 仿真实验

3.1 仿真系统介绍

为了验证提出方法的有效性,文中采用中南大学针对某类高速列车牵引控制系统(TDCS)建立的模拟仿真系统TDCS-FIB2.0进行仿真实验。电路参数见表1。

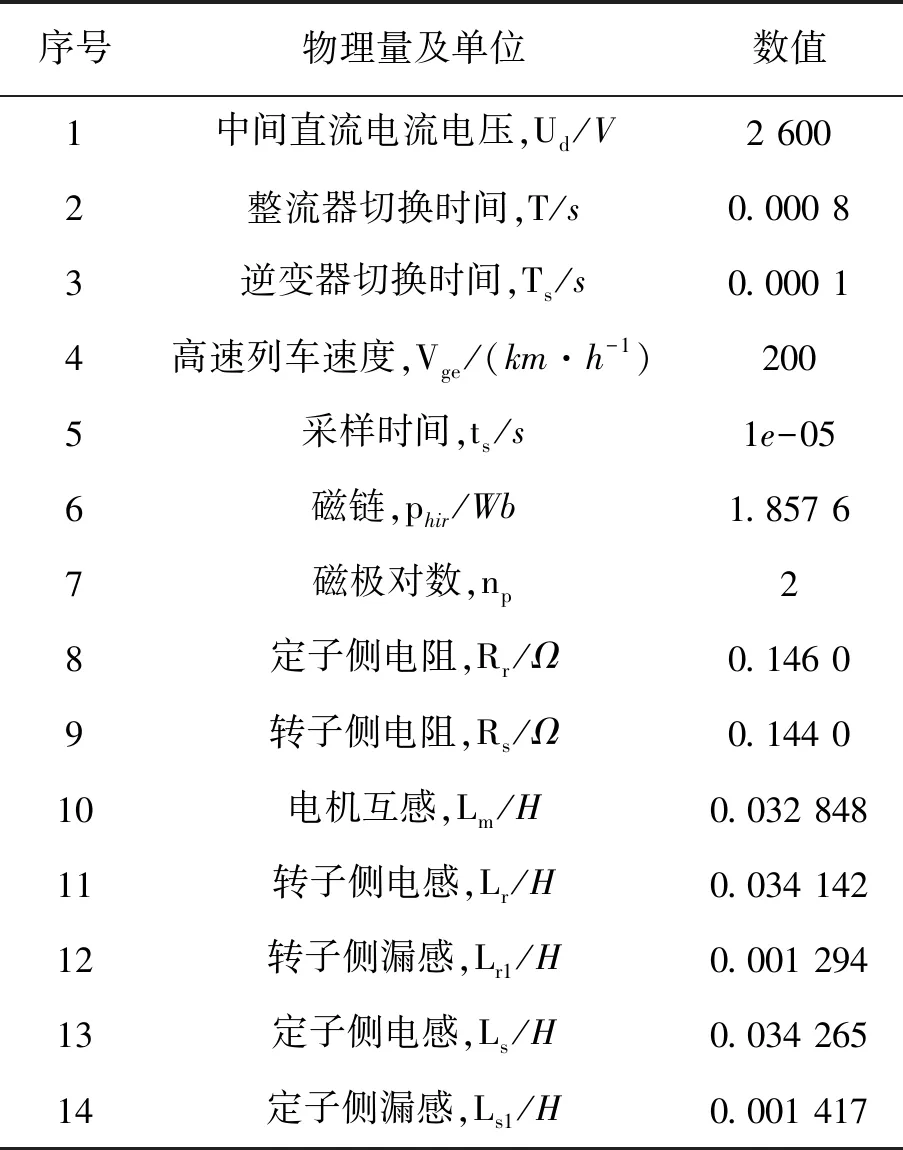
表1 仿真平台电路参数

3.2 故障注入

基于仿真平台注入四种传感器故障,在信噪比30 dB,窗长n=30的条件下进行仿真。

第一类故障f1为传感器,输出值偏离正常值。

第二类故障f2为短路故障,相电压传感器输出值为0。

第三类故障f3为增益故障,输出信号成比例增强。

第四类故障f4为冲击故障,传感器的输出值在某个时刻发生冲击,默认冲击值为100。

每组数据采集20 000个样本,第10 000个样本时注入故障,其中第四类故障f4较为特殊,第10 000个数据时传感器输出值受到冲击,冲击于第12 000个数据结束。

3.3 结果与讨论

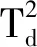
表2 检测性能对比表%

故障f1注入时,如图 2所示。

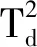
故障f2注入时,如图 3所示。

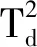
(a) SFA (b) PRSFA

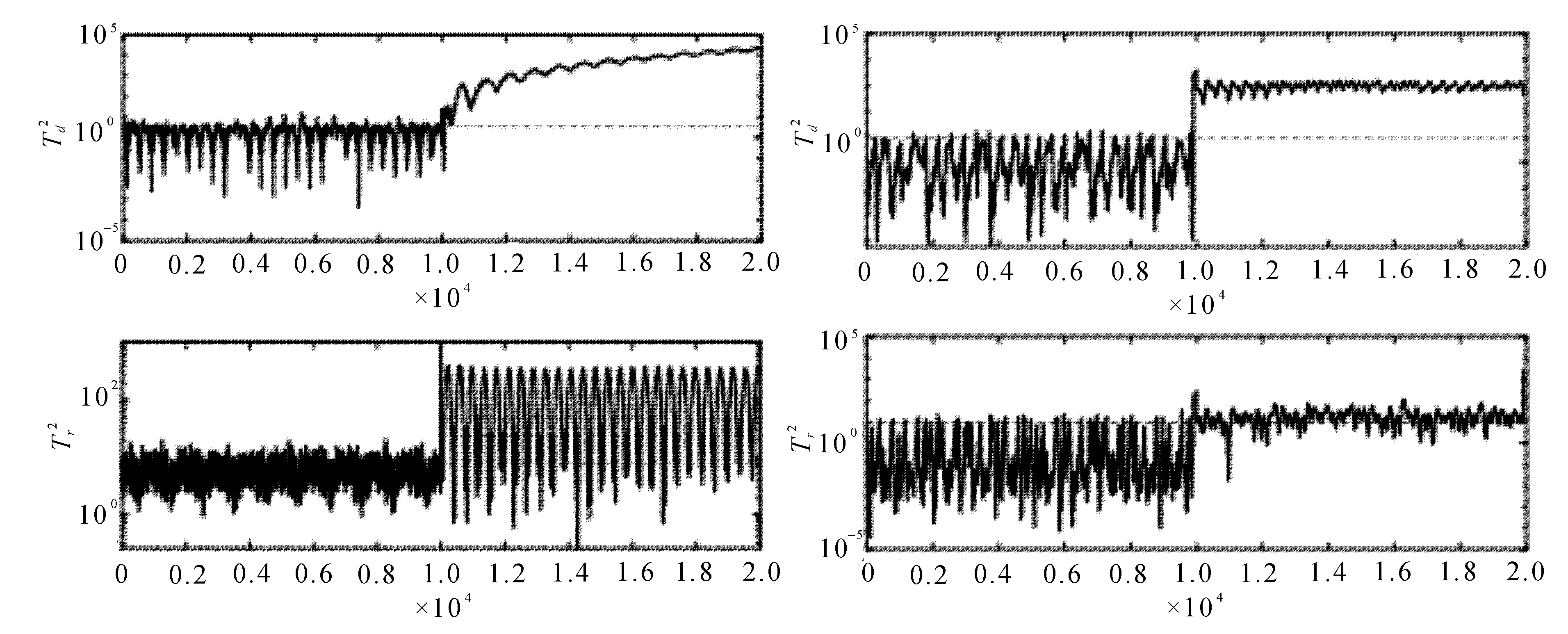
(a) SFA (b) PRSFA

故障f3注入时,如图 4所示。

故障f4是一个传感器冲击故障,如图 5所示。

(a) SFA (b) PRSFA

在第10 000个数据时传感器输出值受到冲击,第12 000个数据时冲击结束,SFA方法和文中提出方法均能表现出其特性,而文中方法显然在故障检测性能上表现更好。

从图表中可以明显看出,四种故障使用SFA方法和文中提出方法均能成功被检出,并具有较低时延。相较于SFA方法,提出的基于概率相关慢特征方法在成功检出故障的同时具有更低的FAR(误报率)和MAR(漏报率),并且文中方法很好地将MAR降低到0,有效地提高了故障检测性能。

4 结 语

对高速列车牵引系统和数据驱动的故障检测方法展开研究,提出PRSFA方法用以减少牵引系统故障检测中漏报和误报问题。文中将KLD散度引入到故障检测方法中,在SFA提取到数据慢特征的基础上,用KL散度计算慢特征的概率密度函数的KL散度距离,充分利用牵引系统故障数据的时间相关性,其有效性在中南大学设计的牵引系统仿真平台的测试中进行了验证。与传统SFA方法相比,文中提出方法有更好的检测性能,更低的FAR和MAR,更加适用于高速列车牵引系统的故障检测。文中工作为高速列车牵引系统的故障检测问题提出一种可执行方案,同时也为后续研究其牵引系统的寿命预测等方面提供了一个新思路。