基于自适应邻域的非均匀点云数据封装方法
郭 敏, 张文丽, 吕源治, 李贞兰
(1.长春工业大学 计算机科学与工程学院, 吉林 长春 130102;2.中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033;3.吉林大学白求恩第一医院, 吉林 长春 130012)
0 引 言
随着三维激光扫描技术的日益成熟,极大地推动了三维重建技术在文物保护、虚拟现实和逆向工程等领域的发展[1-3]。近年来,点云网格化作为三维重建技术的重要处理步骤,被众多研究人员关注。
目前,常用的点云网格化方法主要有3类:基于隐式曲面的方法、基于投影的方法和基于区域生长的方法[4-7]。其中,基于区域生长算法由于思路简单、时间复杂度低的优点被广泛应用。区域生长算法从种子三角形[8]开始,根据一定的约束准则获取最优点[9],实现网格生长。许多学者针对如何选取网格生长范围进行了研究,Bernardinit F等[10]提出BPA方法,通过人为定义滚球半径获取网格生长范围,在点云稀疏区域会出现孔洞。邱春丽等[9]提出基于动态球搜索邻域的算法,能够构建平滑曲面,但是在孔洞周围会生成错误三角形。付永健等[11]提出根据内在属性因子和扩展边关系自适应确定网格生长范围的方法,对于含有孔洞的点云,网格曲面质量会降低。实际应用中,在扫描形状较为复杂的模型时,由于存在视线死角或模型表面粘贴标识点,导致获得的点云数据存在孔洞,且点云分布不绝对均匀[12]。张丽艳等[13]、李松等[14]基于最小角度法修补孔洞,其过程主要分为识别边界、计算孔洞边界夹角和修补孔洞三个步骤。传统的区域生长方法在处理密度非均匀点云时,难以控制网格生长范围,易出现孔洞和网格错乱现象,降低重建精度。
针对上述问题,提出一种基于自适应邻域的非均匀点云数据封装方法,该算法通过点云密度自适应选择合适的空间搜索球半径,控制网格生长范围,优化了最优扩展点的选取,从而减少网格孔洞数量,避免了网格错乱现象。
1 基于自适应邻域的点云网格化算法
基于自适应邻域的非均匀点云数据封装算法整体流程如图1所示。
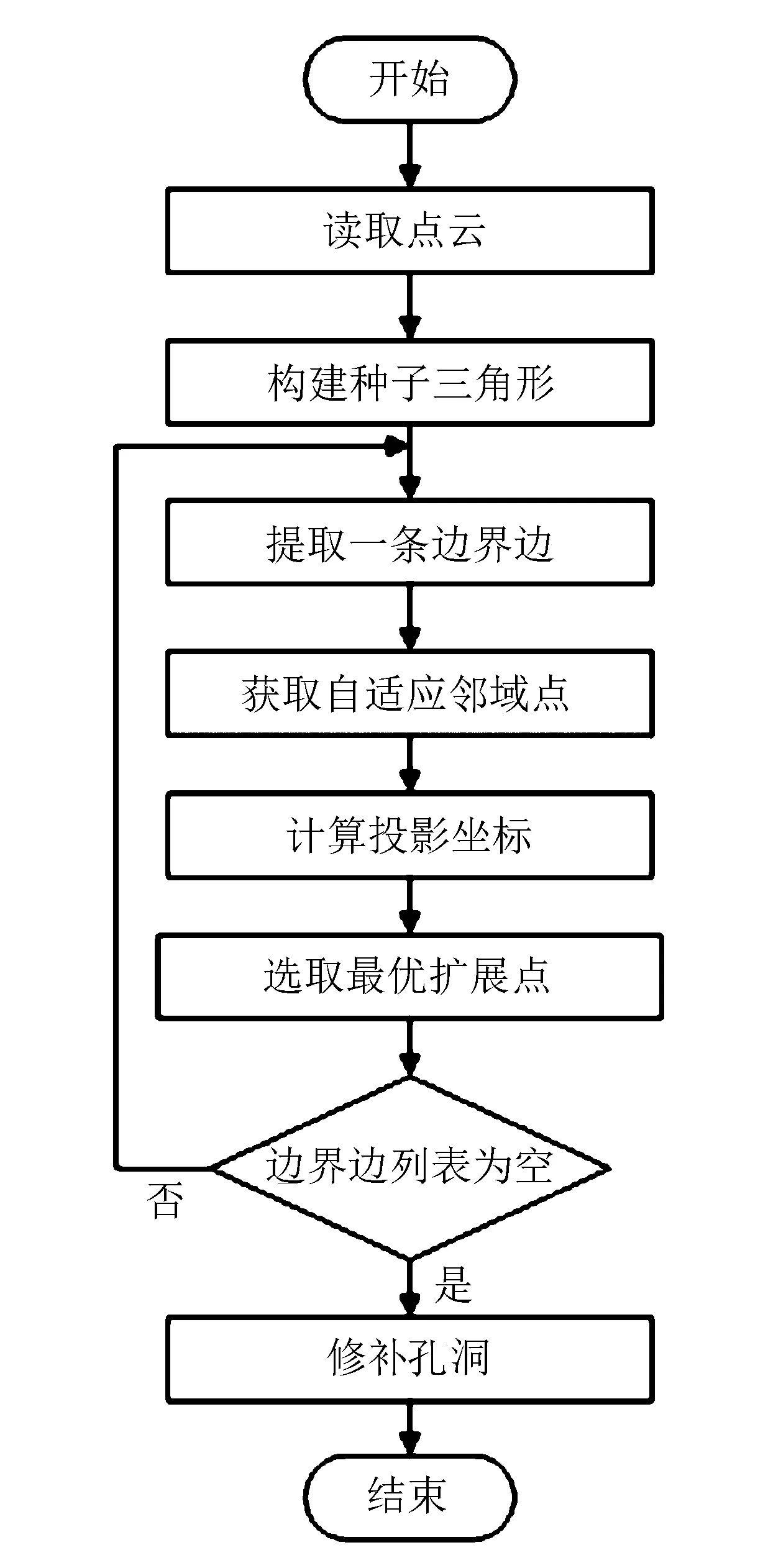
图1 算法整体流程
首先构建种子三角形;其次提取一条边界边,并自适应搜索边界边顶点的邻域;然后将邻域投影到二维平面,计算出投影坐标;再根据约束准则找出最优扩展点,与边界边形成新的三角形,重复之前的步骤,直到边界边列表为空;最后修补网格曲面中的孔洞。
网格质量的评价指标通常为三角形的正则度,即三角形接近正三角形的程度。文中通过三角形内角的余弦和进行计算,
g=2*(cosα+cosβ+cosλ-1),
(1)
式中:α,β,λ----三角形的内角;
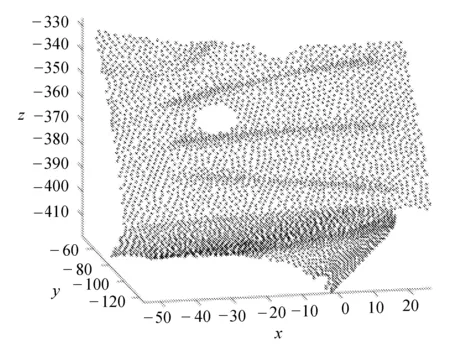
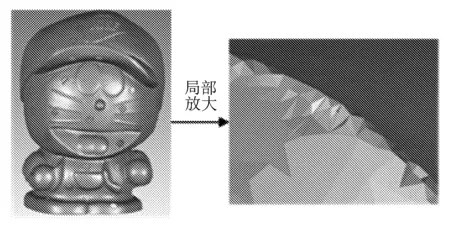
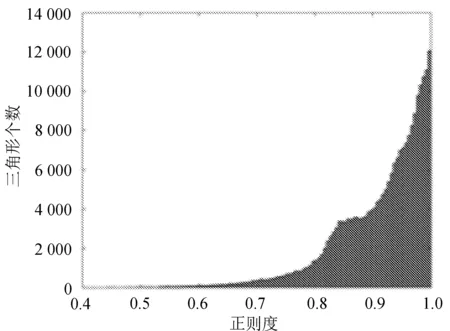
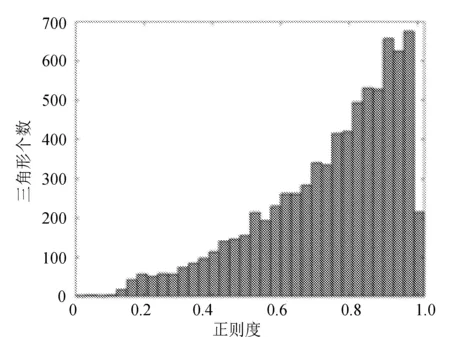
g----三角形正则度,0 为了避免种子三角形穿过网格内部,首先在网格模型的平坦区域选择一点Q1作为种子点,然后找出距离Q1最近的点Q2,再找出与Q1、Q2距离和最小的点Q3,则Q1、Q2、Q3就是种子三角形的三个顶点。Q1作为种子点要求所有邻域点的法向量与Q1法向量的夹角均小于90°。 采样后的三维点云数据如图2所示。 图2 三维点云(机器猫胡须部分) 从图2可以看出,在细节特征丰富的地方点云分布相对密集,其它地方的点云分布相对稀疏。 由于点云密度不均匀,当网格生长范围限定不适当时,容易出现孔洞,而且会影响后续的最优点选择,导致网格出现交叠。因此,文中根据点云密度设置自适应的搜索球,以优化网格生长范围。 通过计算点云中各点的距离平均值来估算点云密度,点云的平均距离密度一般为 (2) 式中:d----点云中某一点与距离这点最近点的距离; N----点云中数量。 平均距离E越大,表示点云分布越稀疏,平均距离E越小,点云分布越密集。 设PC为点云集合,Pi(Pi∈PC|i=1,2,…,N)为目标点,作球心为Pi,半径为r的空间搜索球。根据点云平均距离密度E确定空间搜索球的初始半径为 R1=S*E, (3) 式中:S----倍数。 由目标点Pi的初始空间搜索球可以确定Pi的邻域点Qj(j=1,2,…,M),定义Pi的邻域平均距离为 (4) 文中算法的r值仅与S相关,参数只有S一个,自动化程度较高。由于S的大小影响r的大小,如果S过小,此时模型重建不完整;如果S过大,此时程序运行时间增大。文中为了确定合适的参数S,对点云进行多次曲面重建实验,最终根据三角形的正则度、数量以及网格孔洞数量选取曲面质量最优时的S值为3.5。 将边界边顶点P1、P2的邻域Qj(j=1,2,…,M)投影到平面时,可分为两个步骤: 1)将邻域点投影到切平面。计算P1、P2的中点P(Px,Py,Pz)的法向量n1=(nx,ny,nz),由P点的坐标和法向量可以确定切平面方程为 nx*(x-Px)+ny*(y-Py)+nz*(z-Pz)=0, (5) (6) 式中:θ----局部平面法向量n1和xoy面法向量n2的夹角; k----向量n1和n2的叉积。 I是3×3的单位矩阵,若 则 (7) 选取最优扩展点就是在扩展边顶点的邻域中,利用约束准则选取一个最优的邻域点,与扩展边形成新的三角网格。 1.4.1 平面约束准则 三角形空外接圆准则、三角形内角约束准则和小三角形准则。 1.4.2 空间二面角准则 空间二面角示意图如图3所示。 图3 空间二面角示意图 △ABC是已生成三角形,AB是生长边,D是扩展点,计算△ABC和△ABD的夹角,即计算它们法向量nABC和nABD的夹角,夹角越接近180°,相邻三角形的过渡越平稳。此外,二面角过小时,三角形之间可能会形成交叠,因此需要设置一个最小阈值βmin,文中阈值βmin设置为π/3。 由于重建曲面存在部分孔洞,为了获得完整的模型,需要对孔洞区域进行修补。 基于最小角度法修补孔洞,该方法主要包括识别边界、计算孔洞边界夹角和修补孔洞三个步骤。如图4所示。 图4 孔洞修补示意图 (8) 当f≥0时,孔洞多边形是逆时针方向,否则是顺时针方向,进而求出夹角大小。在计算孔洞边界夹角后,通过孔洞边界长度、边界点的距离和孔洞边界夹角计算新增点Enew,并去除边长和内角不满足阈值的三角形。 1)为验证文中算法,以机器猫石膏像点云为实验数据,该点云由中国科学院长春光学精密机械与物理研究所自主研发的SVision751B型三维激光扫描仪扫描得到。 2)为验证文中算法的有效性,将其与传统区域生长网格化算法的结果进行对比分析。 两种方法的对比结果如图5所示。 (a) 传统区域生长网格化算法 图5(a)是传统区域生长网格化算法结果,存在局部区域网格错乱现象,图5(b)是文中算法结果,在图(a)的相同位置,没有网格错乱现象,且三角形形态良好,能够准确地表达眼睛、鼻子等细节特征信息。 文中采用正则度对网格质量进行评价,两种结果的正则度直方图反映了正则度大小与三角形个数的关系,如图6所示。 (a) 传统区域生长网格化算法 通过比较图6中的两幅图可知,两种方法的正则度大小及所占三角形数量基本相同,大多数正则度在0.8~1.0,极少数小于0.5,狭长三角形数量不多。网格化结果数据见表1。 表1 网格化结果数据 由表1可知,与传统区域生长网格化算法相比,文中算法更大程度地利用了点云数据,同时三角形个数增加0.213 5%,相应的孔洞数量减少20.114 9%。 综上,文中算法略优于传统区域生长网格化算法。 孔洞修补效果如图7所示。 (a) 孔洞修补前 图7(a)是孔洞修补前的网格曲面,含有若干由于模型表面粘贴标识点而形成的孔洞,图(b)是孔洞修补后结果,网格孔洞基本修补完成。 孔洞修补结果数据见表2。 表2 孔洞修补结果数据 结合表2可知,修补过程中三角形数目增加3.551 3%,网格顶点个数增加2.599 3%,且修补前点云平均密度为1.442 6,修补后孔洞区域网格顶点平均密度为1.478 3,网格密度接近周围网格。修补孔洞产生的三角形的正则度分布情况如图8所示。 图8 孔洞修补网格正则度直方图 由图8可知,正则度在0.8~1.0的占比49.839 5%,0.5~1.0的占比86.416 7%,狭长三角形较少。 针对密度非均匀点云重建时难以控制网格生长范围问题,文中对基于自适应邻域的非均匀点云数据封装方法进行了研究,在保证正则度和三角形数量的前提下,减少了狭长三角形和网格孔洞的数量,有效解决了局部网格错乱问题。实验结果表明,文中算法可以有效、准确地构建出质量较好的三角网格模型,具有一定的实用性。1.1 构建种子三角形
1.2 基于点云密度的自适应邻域选择

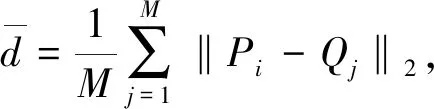
1.3 投影到平面

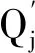
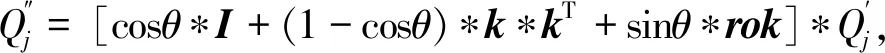
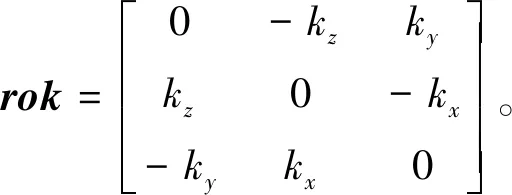
1.4 选取最优扩展点

1.5 修补孔洞
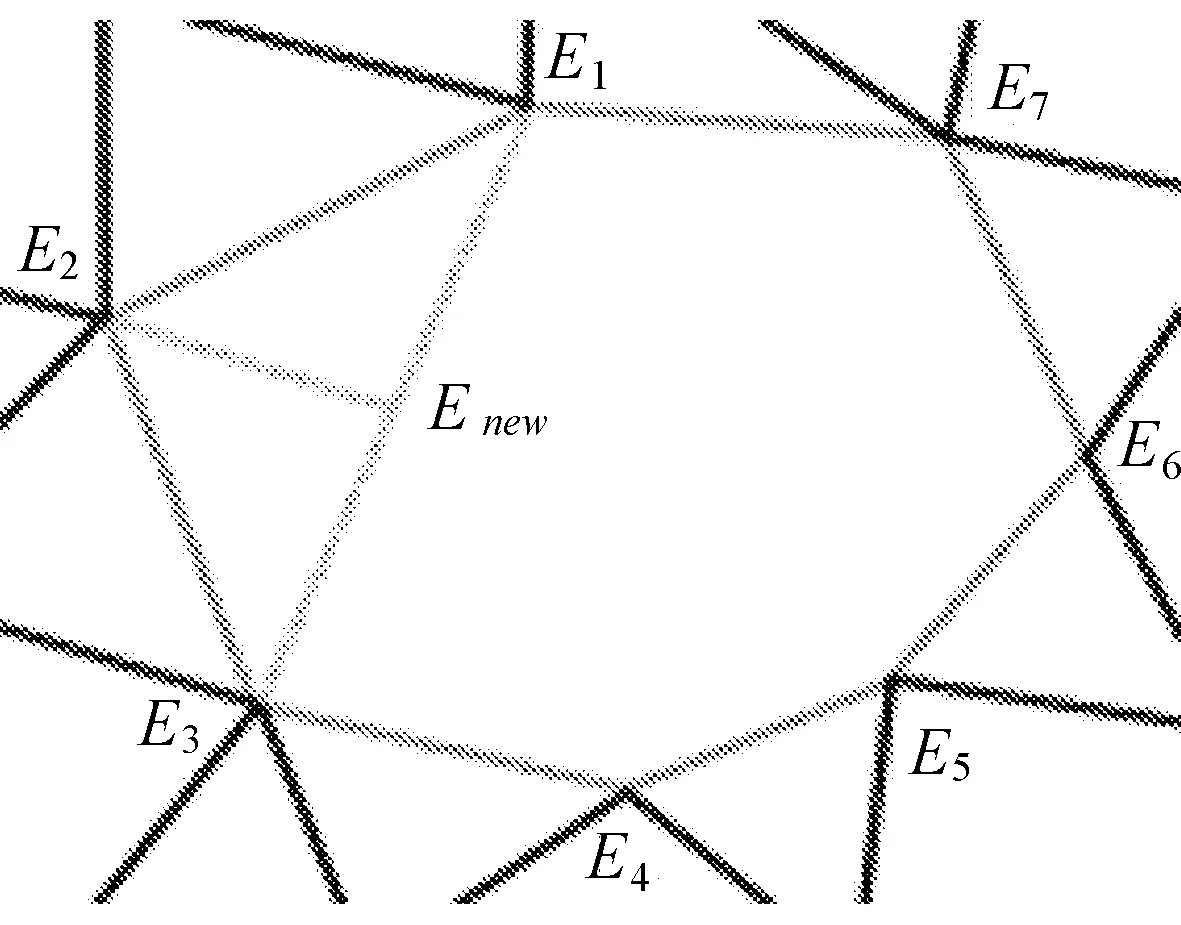
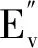
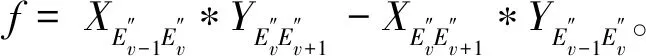
2 实验结果与分析



3 结 语

