运用格子Boltzmann方法求解空间分数阶方程

李 康, 张建影

(长春工业大学 数学与统计学院, 吉林 长春 130012)

0 引 言

近年来,分数阶偏微分方程受到越来越广泛的关注,学者对于不同方程的数值解进行了大量研究,如分数阶扩散方程[1-6]、分数阶Navier-Stokes方程[7]、分数阶平流扩散方程[8-11]、分数阶反应扩散方程[12]等。对于导数项是分数阶的偏微分方程,一般来说,求解方法主要为数值求解,因为只有极少数特殊的分数阶偏微分方程可以得到解析解[11],应用范围并不广泛,因此主要通过数值方法得到方程的近似解。

对于计算分数阶偏微分方程,部分学者采用有限差分法[1,2,9],也有部分学者用有限元法[5]、有限体积法[4]。近年来,由于格子Boltzmann方法在求解其他的线性和非线性偏微分方程[13]取得了满意的成果,所以部分学者开始对格子Boltzmann方法求解分数阶偏微分方程进行研究[14-18]。从目前研究结果看,用格子Boltzmann方法构建的模型可以准确恢复出宏观连续方程,并且通过数值模拟验证了数值计算的准确性和有效性,所以LBM在分数阶微分方程上的应用还具有广阔前景。

文中主要采用格子Boltzmann方法,对扩散项含有分数阶导数的情况进行处理后,求解如下形式的一维Riesz空间分数阶偏微分方程:

(1)

式中:α----Riesz空间分数阶导数的阶数,1<α<2;

kα----扩散系数;

s(y,t)----源项;

g(y)----初始条件;

h1(t),h2(t)----边界条件。

1 Riesz空间分数阶Navier-Stokes方程的预处理

首先,需要将方程中Riesz空间分数阶导数项进行处理。文中采取将Riesz空间分数阶导数进行离散化处理的方法。

Riesz空间分数阶导数的定义式为

(2)

其中

(3)

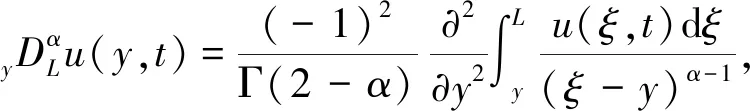
(4)

分别是左侧和右侧的Riemann-Liouville分数阶导数。

方程(1)中Riesz空间分数阶导数项为

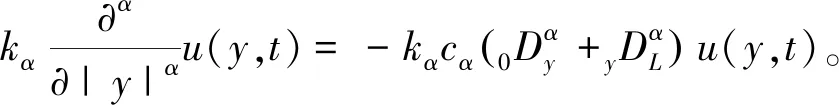
(5)

根据Riemann-Liouville分数阶导数定义,利用数值积分公式可将式(5)化简为

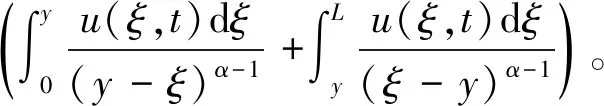
(6)

式(6)中左积分又可以化简为

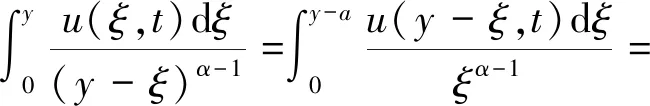
(7)

令

则式(6)中左积分

同理,式(6)中右积分也可化简为

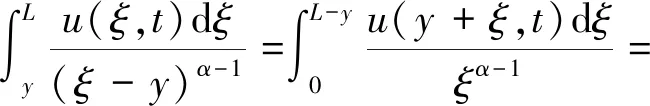
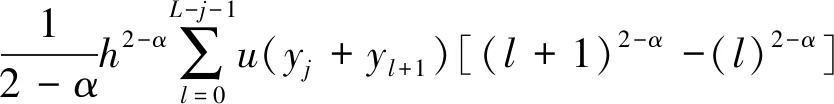
(8)

令

则式(6)中右积分

通过以上处理,方程(1)中的扩散项可以变为

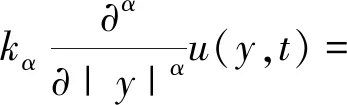
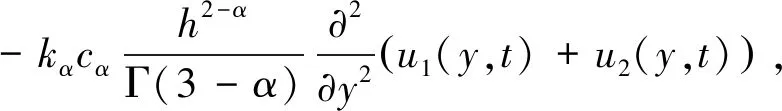
(9)

再令

则方程(1)可以变为

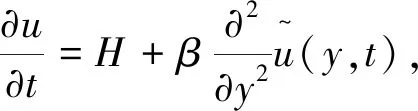
(10)

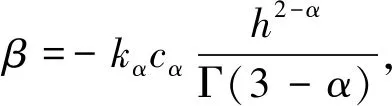
(11)

式中:H----源项;

β----扩散系数。

2 构造格子Boltzmann模型

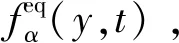
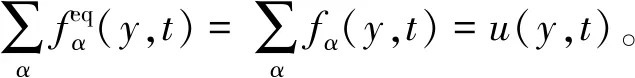
(12)

格子Boltzmann方程可以写成

fα(y+εeα,t+ε)=fα(y,t)-

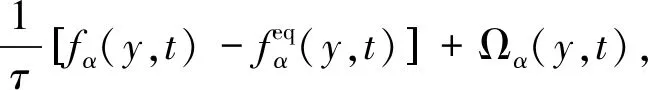
(13)

式中:τ----单松弛时间因子,是一个常数;

L----特征长度。

我们假设在数值模拟中,克努森数ε等于时间步长Δt。

对式(13)进行Taylor展开,可以得到

fα(y+εeα,t+ε)-fα(y,t)=

(14)

在小的克努森数ε的假设下,对上述式子中的fα(y,t)进行Chapman-Enskog展开

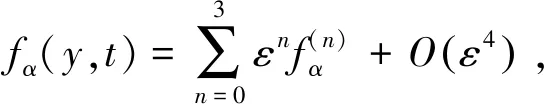
(15)

为了讨论不同时间尺度的变化,采用多尺度分析,引入t0,t1,t2,t3作为时间尺度。

tn=εnt,n=0,1,2,3,

(16)

并且

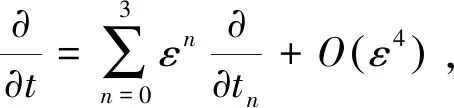
(17)

同时假设源项为

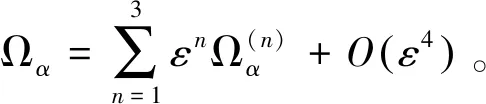
(18)

将上述展开式(12)、式(13)、式(15)、式(16)都代入格子Boltzmann方程中,可以得到关于ε阶的方程

(19)

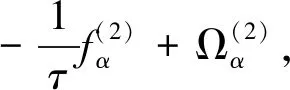
(20)

其中,系数Ci为

偏微分算子

将式(17)+式(18)×ε,并且令

可得

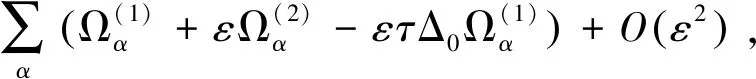
(21)

为了恢复出宏观方程(1),我们假设平衡分布函数满足以下条件

(22)

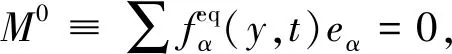
(23)

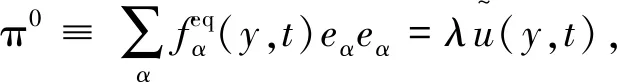
(24)

则可以推出平衡分布函数为

(25)

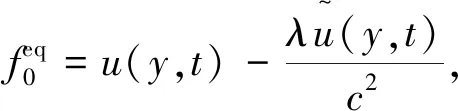
(26)

β=-ελC2,

(27)

式(21)可以变为

（二）从材料包含的知识深度上看，要做到“三个思考”，即是什么，为什么，怎么样。深层次解读信息，是什么（什么现象、问题的实质）、为什么（原因、作用、危害等）、怎么样（措施、建议、态度等）。当然，不一定每题都同时回答三个层次，通常用在认识、评价类试题，要根据问题并结合材料做到具体问题具体分析。

(28)

其中β=-λεC2是扩散系数,

我们选择

所以

3 数值模拟

为了说明该算法的有效性,我们用下面的数值算例去验证。

算例1 两平行板间的压力驱动流动(Riesz空间分数阶Navier-Stoke方程)

(29)

这个方程的精确解是

u(y,t)=y2(1-y)2tα。

我们给出全局相对误差(R)和最大绝对误差(E)的定义

(30)

(31)

式中:u(yi,t)----在(yi,t)处u的数值解;

u*(yi,t)----在(yi,t)处u的精确解。

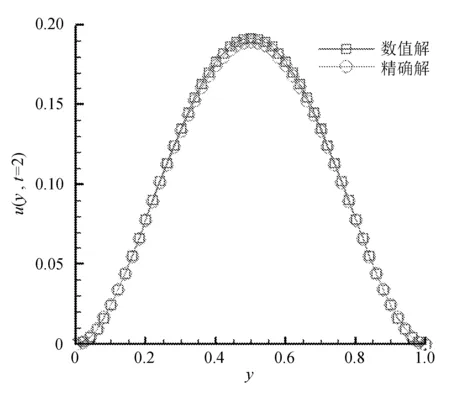
图1 数值解与精确解对比

图中空间步长h=0.02,时间步长Δt=0.025,空间分数阶α=1.6,Re=1 000,时间t=2时,数值解与精确解的对比。

从图1可以看出,数值解与精确解比较吻合,该算法适用于Riesz空间分数阶方程。

该算例收敛阶的对数图像如图2所示。

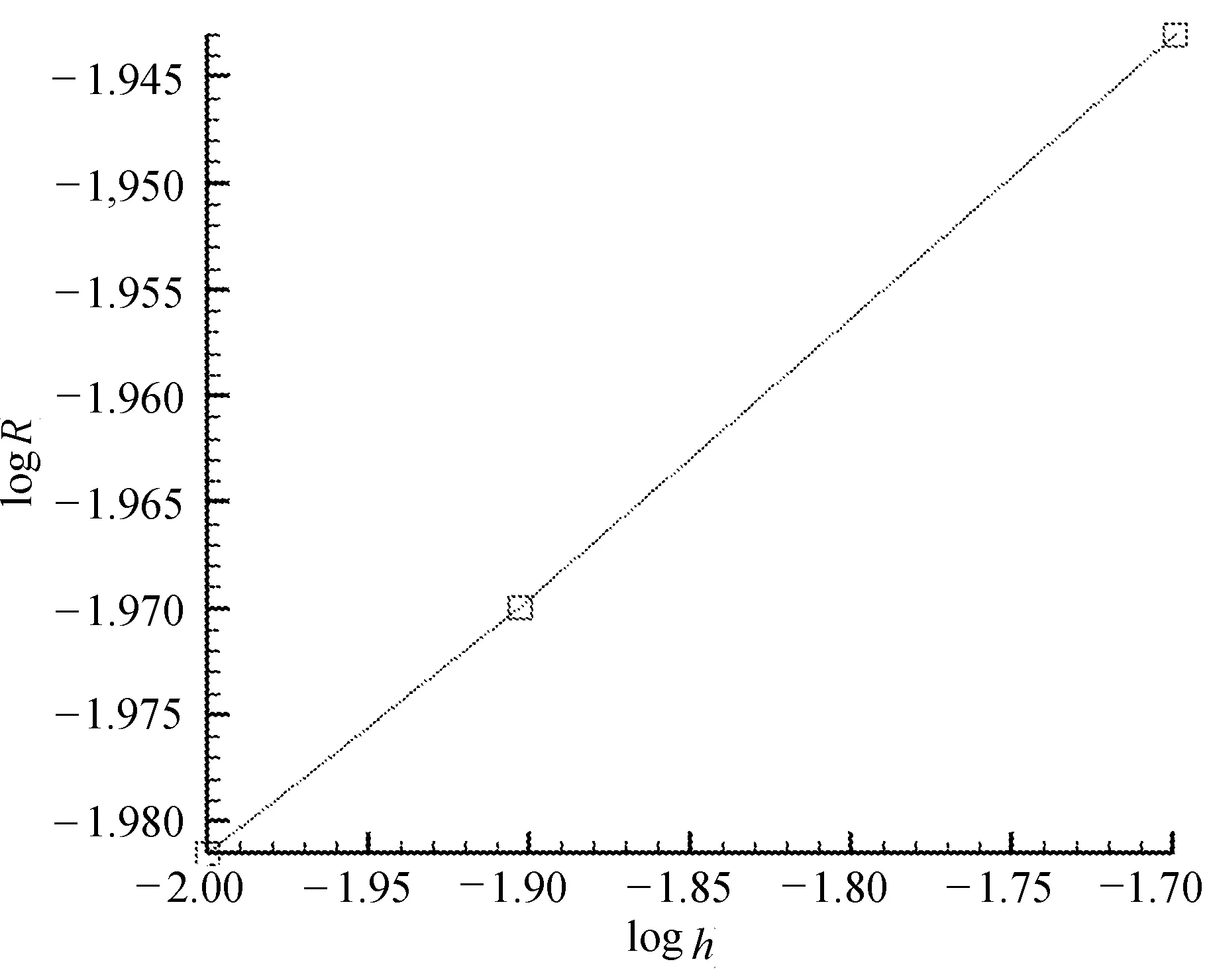
图2 算法收敛阶的对数图像

图2中横坐标是空间步长h的对数,纵坐标表示全局相对误差R的对数。经过数据拟合后得出的收敛阶为1.286。改变参数时数值解的对比如图3所示。

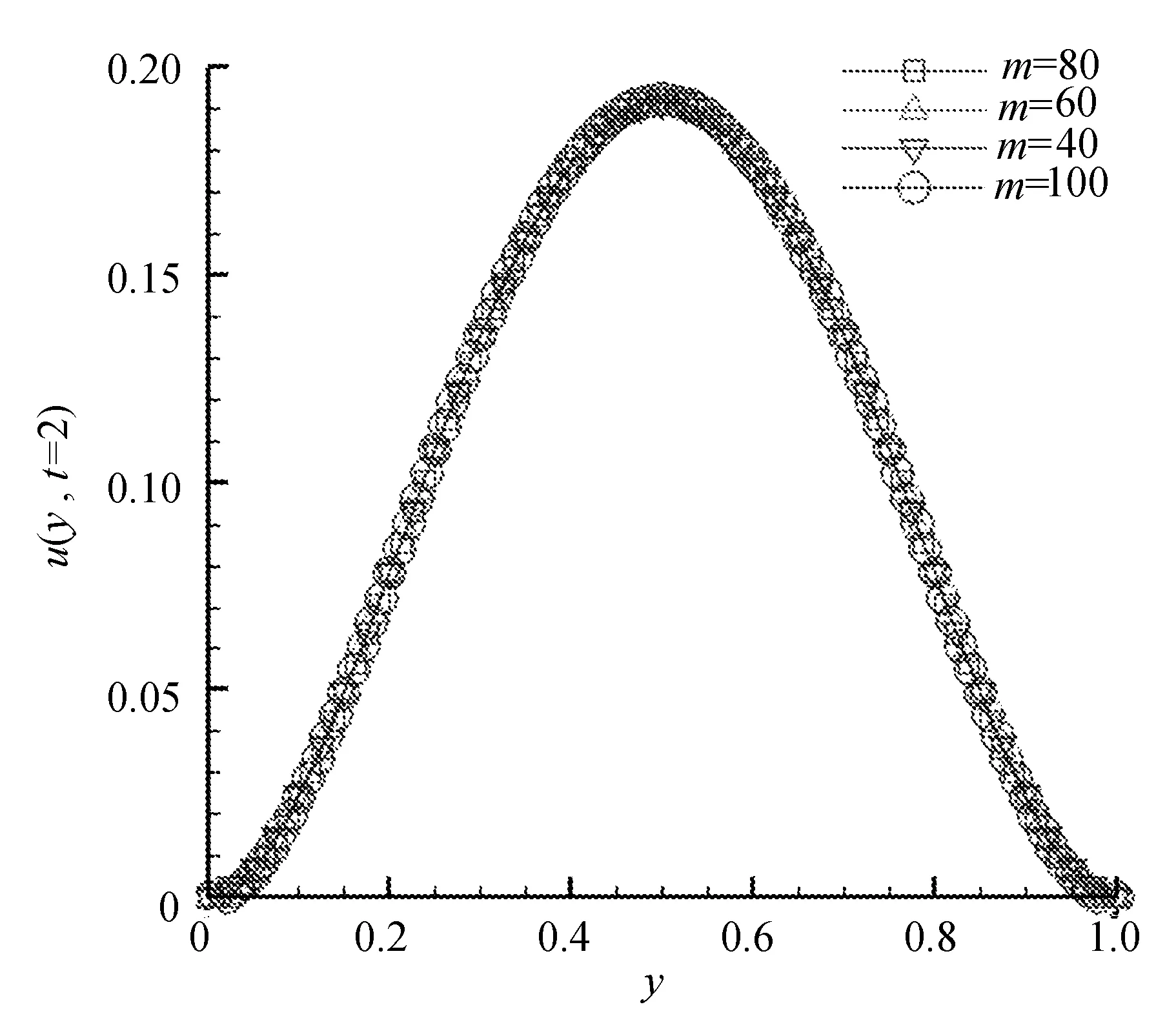
(a) 改变网格数m

从图3可以看出,改变网格数m以及时间步长Δt数值解并没有明显变化。与传统的数值方法(有限差分法、有限元法)求解Riesz空间分数阶方程相比,格子Boltzmann方法求解方程时物理意义更加清晰,边界条件易于处理,可以模拟各种复杂的宏观现象,同时编程比较容易,计算前后处理也比较简单,避免了冗长复杂的网格划分过程,可以提高计算效率。

图3(a)中m取值分别为40,60,80,100,其余参数取值不变。图(b)中Δt取值分别为0.01,0.02,0.05,其余参数取值不变,(b)中dt表示为Δt。

算例2 Riesz空间分数阶扩散方程

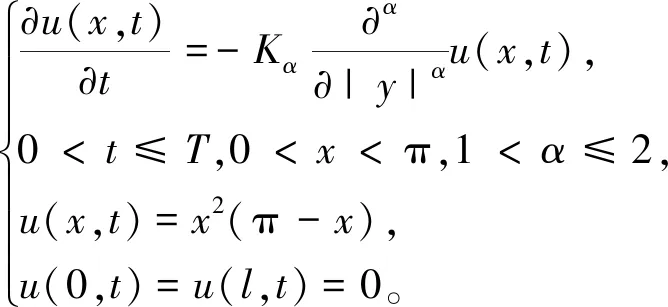
(32)

这个方程的解析解为

其中bn的表达式为

数值解与解析解对比如图4所示。

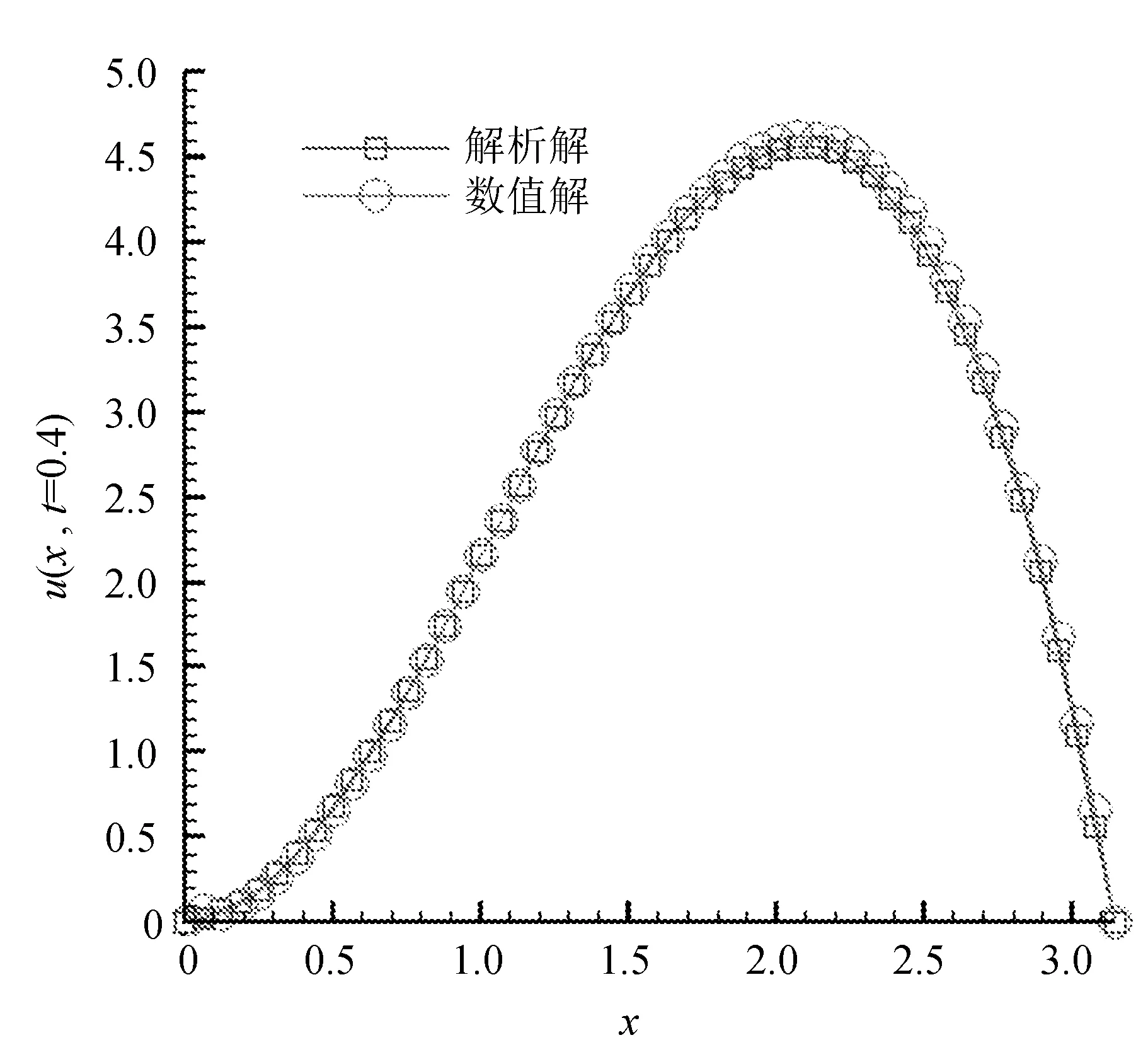
图4 数值解与解析解对比

图4是网格数m为50,时间步长Δt为0.015,时间t为0.4,扩散系数kα为0.01,空间分数阶α为1.8时,通过该方法所得的数值解(RJ)与解析解(R)的对比图,从图中可以看出,该方法得到的数值解与解析解比较吻合,适用于求解此方程。

改变参数时,数值解的对比如图5所示。

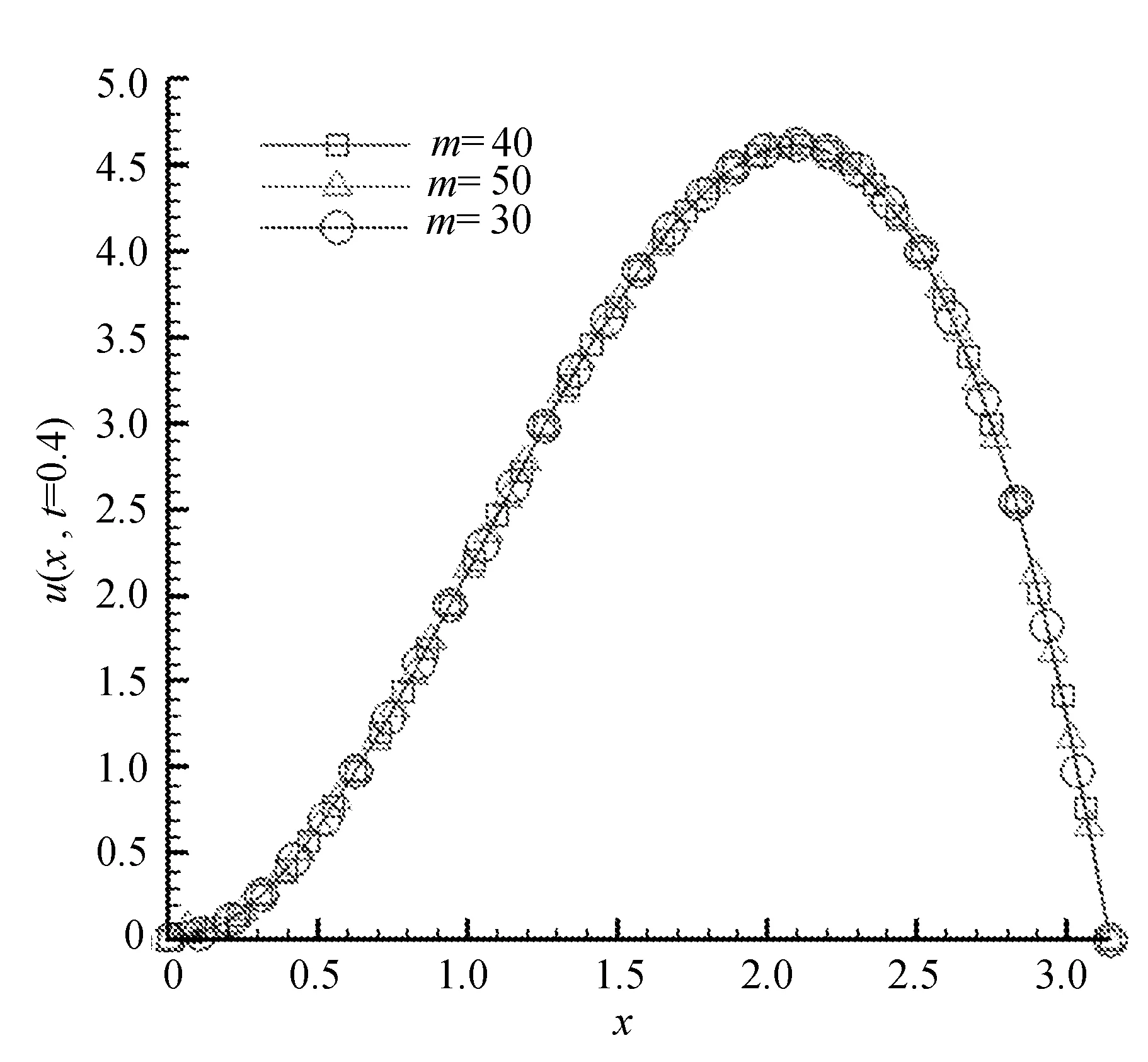
(a) 改变算法中的网格数m

图5(a)中m取值分别为30,40,50,其余参数取值不变。图5(b)中Δt取值分别为0.005,0.015,0.025,0.050,其余参数取值不变,(b)中dt表示为Δt。

从图中可以看出,改变网格数m以及时间步长Δt数值解并没有明显变化。

4 结 语

通过格子Boltzmann方法求解一维Riesz空间分数阶偏微分方程,通过对Riesz空间分数阶进行离散化处理,得到近似标准的扩散方程,并且通过LBM的D1Q3模型,恢复出宏观方程,同时计算出平衡态分布函数。通过两个带有解析解的Riesz空间分数阶偏微分方程进行数值验证,对比发现数值解与解析解能够很好吻合。格子Boltzmann方法求解Riesz空间分数阶方程时物理意义更加清晰,边界条件易于处理,编程计算过程比较简单,避免了冗长复杂的网格划分过程,可以提高计算效率。