基于改进遗传算法求解容量约束车辆路径问题
刘祥坤, 李万龙, 李东升, 牛家冰
(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)
0 引 言
车辆路径问题(VRP)最早由Dantzig G B等[1]于1959年提出,该问题也被证明属于NP-hard问题,随着研究的深入,该问题的研究范围也不仅仅局限在简单的车辆路径问题,如容量限制车辆路径问题、有时间窗口限制的车辆路径问题等。
文中主要研究了容量约束车辆路径问题(CVRP),CVRP是在传统CRP问题的基础上,加入了车辆容量约束,主要解决多辆有容量约束的配送车辆向多个服务点进行服务,如何设计配送车辆的行驶路径,使得服务成本最低的问题。由于该问题属于NP-hard问题,精确算法并不能在合理的时间内得到满意的结果,人们的研究也从精确算法转向了启发式算法。Wu Y F等[2]提出一种基于蚁群优化的改进混合ACO-VNS算法和可变邻域搜索算法,该方法在更短的时间内取得了更好的性能;Asma M等[3]通过萤火虫算法与两种类型的局部搜索和遗传算子结合,提高了解的质量,并加快了收敛速度;蔡延光等[4]提出一种带分裂机制的帝国竞争算法求解,结合2-opt局部搜索算法,有效求解CVRP问题;王丹等[5]采用新染色体表示和不同交叉操作、变异操作策略,依据基准数据集和测试数据验证了NGA算法,有效解决了问题;曹炳汝等[6]提出在多车型动态需求车辆配送模型,采用遗传算法求解一条最优路线;韩孟宜等[7]根据实际条件构建了有时间限制的应急物资配送模型,遗传算法通过结合节约算法、大规模邻域搜索算法,设计了一种混合遗传算法。
目前对该模型的求解主要用到的启发式算法为蚁群算法[8-10]、遗传算法和粒子群算法[11-12]等。文中在传统遗传算法的基础上对种群初始化和选择操作、交叉操作、变异操作进行了改进,同时结合邻域搜索算法进行改进,以达到最短时间内求出最优解或次最优解。
1 CVRP数学模型
CVRP问题描述:设某仓库有m辆配送车,该仓库需要向N个客户运输物资,每个客户的物资需求量为Qi(i=1,2,…,N),每辆车的最大载货重量为Qmax,dij为节点i和节点j之间的距离。如何使所有车辆行驶的总距离最短是本问题研究目标,对该问题进行如下假设:
1)仓库以及各个客户位置已知,且所有客户与仓库之间互通,配送车辆从仓库出发,最后返回到仓库;
2)每个客户只能由一辆配送车辆进行配送,不能由多辆车进行多次配送;
3)单个客户的需求量小于等于车辆的最大配送量;
4)所有车辆规格相同,每辆车只安排一次配送任务。
本问题目标函数为配送过程中所有配送车行驶的总路径长度,则问题模型如下:
目标函数为
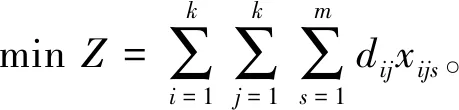
(1)
约束条件为
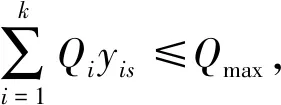
(2)
s=1,2,…,N,
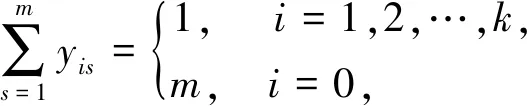
(3)

(4)
j=1,2,…,N;s=1,2,…,m,

(5)
i=1,2,…,N;s=1,2,…m,
其中,式(2)是保证每辆车的配送物资不超过配送车辆的最大载货重量,式(3)~式(5)是保证每个客户只能由一辆车提供配送。
2 求解过程
传统遗传算法随着迭代次数的增加,种群多样性下降迅速,导致算法搜索能力降低,文中通过对基本遗传算法的操作进行改进,增加搜索范围,避免陷入局部最优,提高解的质量。
2.1 染色体编码
文中选用实数编码进行染色体的构造,将客户点和车辆分别进行编码,客户编码为(1,2,…,N),车辆编码为(1,2,1,3,…,k),其中N为客户数量,K为该次运输所需要的车辆数。如客户染色体为“1,2,3,4,5,6,7”,车辆染色体为“1,3,1,2,3,1,2”表示的路线为:
子路线1:仓库0-客户1-客户3-客户6-仓库0;
子路线2:仓库0-客户4-客户7-仓库0;
子路线3:仓库0-客户2-客户5-仓库0。
2.2 种群初始化
先采用随机生成法生成一条合理的路径,然后通过变邻域搜索算法对该路径进行不断交换、替代、倒置等优化操作,直至所有客户点遍历完成,形成一条更加合理的路径,将该个体加入到种群中,循环重复该过程直到达到种群数量。通过该方法构建种群,提高了初始种群的质量,从而加快了算法的求解速度。
2.3 计算适应度值
个体的好坏由个体的适应度值决定,个体在种群的适应度值越大,则代表该个体在种群中越优秀,被保留下来的概率也越大,由于CVRP的目标是使总的运输距离最小,所以需要将目标函数进行转换,适应度函数为:

(6)
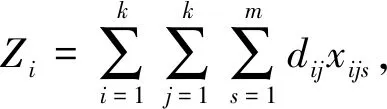
(7)
式中:Zi----该个体对应的目标函数值(该个体的运输距离);
N----客户的个数。
2.4 选择操作
通过精英保留策略和轮盘赌对个体进行选择,算法初期由于种群个体较差,不宜保留过多精英个体,通过动态调整精英个体数量来加快算法的求解速度,其基本步骤为:
1)计算种群所有个体适应度值,并按照从大到小依次排序;
2)根据式(8)确定当前保留优秀个体数量,剩余个体则按照轮盘赌的方式进行选择。
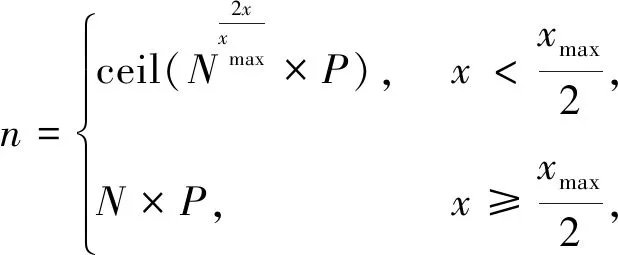
(8)
式中:ceil----向上取整;
N----种群个体数量;
P----优秀个体占总个体的比例;
x----当前迭代次数。
由于算法迭代初期不存在优良个体或优良个体较少,若使用固定数量的保留策略,则会影响种群的多样性,从而造成搜索范围的减少,而动态精英保留策略在算法迭代初期,保留数量较少,不会对种群多样性造成破坏。到了算法后期,个体达到最优或接近最优,此时保留数量增加,又可以避免个体被破坏。
通过该选择策略,既避免了轮盘赌导致的随机误差,又提高了种群的多样性,保证了算法的收敛速度。
2.5 交叉操作
交叉操作是种群新个体产生的主要来源,遗传算法在开始时由于种群种类丰富,但是解的质量并不高,适当提高种群的交叉概率以提高寻优速度,而到了算法后期,个体解的质量都接近最优解,此时适当减小种群的交叉概率可以避免交叉对优质解的破坏。
文中对交叉概率进行改进,改进的交叉概率为

(9)
式中:Ps----初始交叉概率;
fa----当前种群的平均适应度值;
f′a----种群初始平均适应度值。
文中对染色体的交叉采用单点交叉与两点交叉结合方式,其基本步骤如下:
1)以一定的概率Pc随机选择单点交叉或两点交叉。
2)若选取单点交叉,以父亲染色体起点到切点之间的基因作为孩子染色体的初始状态。依次遍历母亲染色体,若当前孩子染色体长度小于L,将孩子不存在的基因在孩子初始染色体头部依次加入,否则在当前孩子染色体的末尾加入,如图1所示。
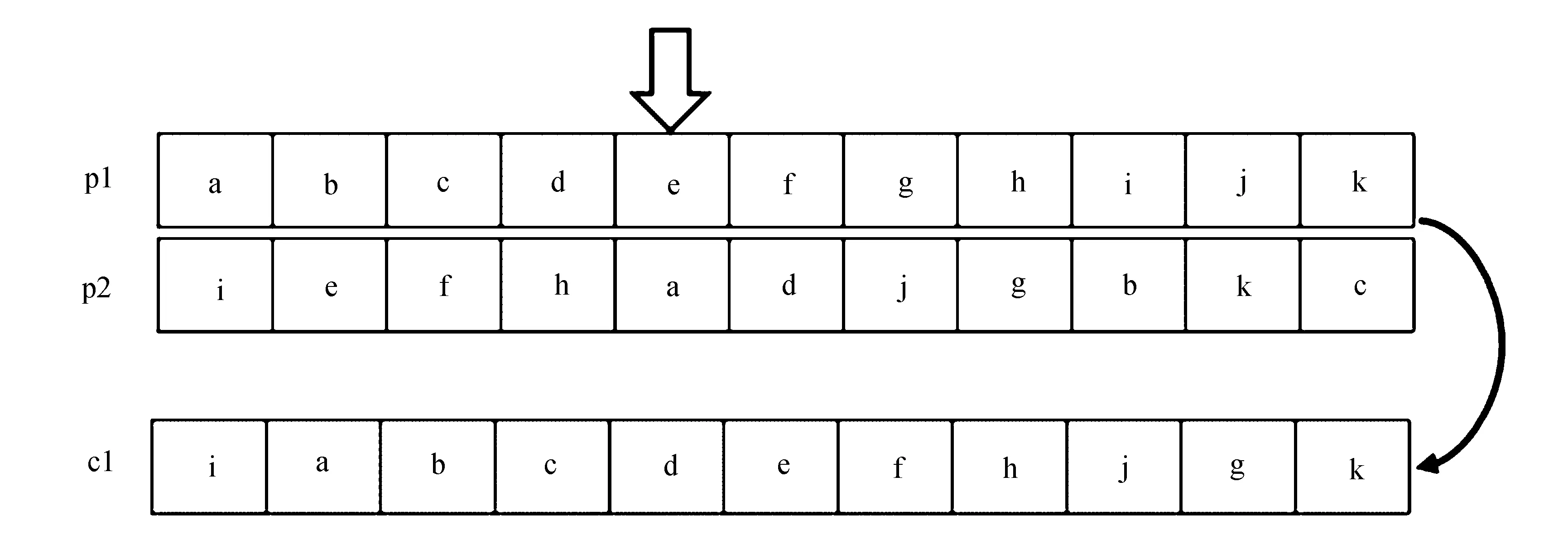
图1 单点交叉示意图
3)若两点交叉,以父亲染色体切点X与Y之间的基因作为孩子染色体的初始状态。依次遍历母亲染色体,若当前孩子染色体长度小于L,则在切点X前依次加入,否则在当前孩子染色体末尾加入,如图2所示。

图2 两点交叉示意图
L=N-X,
(10)
式中:N----客户数量;
X----第一个切点的位置。
2.6 变异操作
变异操作是种群产生新个体的另一种方法,若变异概率恒定,则可能造成优秀个体的丢失,为了保存种群的优秀个体,文中采用动态调整变异概率的方式来实现优秀个体的保留。每个个体的变异概率为

(11)
式中:fi----当前个体的适应度值。
采用两点互换的操作进行染色体的变异操作,即在个体中随机选择两个不同的基因位置进行交换,如图3所示。
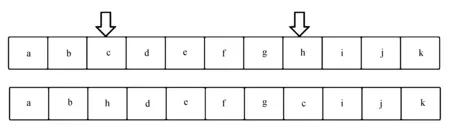
图3 变异操作示意图
2.7 变邻域搜索算法
由于遗传算法本身存在局部搜索能力不足的缺点,虽然也能够以一定的概率找到最优解,但是要花费很大的时间代价,为了扩大搜索算法的搜索空间,文中在遗传操作之后加入了变邻域搜索算法,通过将遗传算法与邻域搜索算法进行结合,更好地提高解的质量与求解速度。文中设计了2-opt法、两点交换法和单点插入法,这些算法不仅无需复杂的参数设置、设计简单,而且加快了遗传算法寻优的速度。
1)2-opt是求解路径最常用的局部搜索算法,即
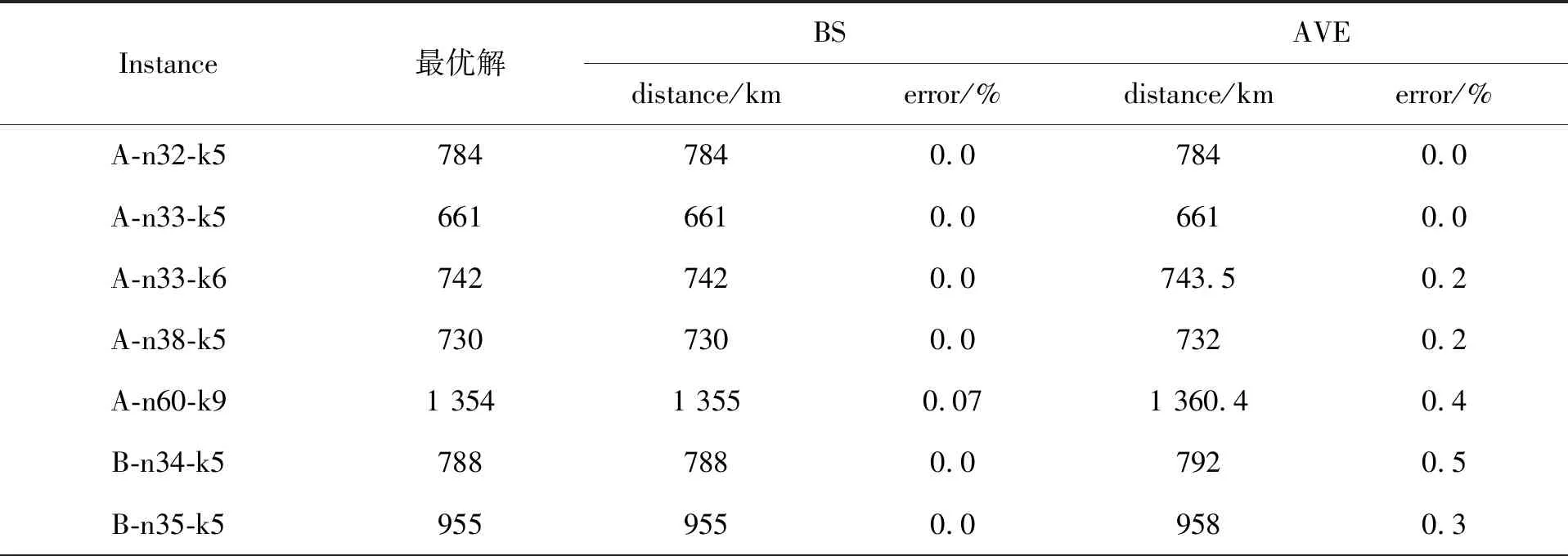
ab+cd 则删除边ac与bd,连接ab与cd,并把顶点b与c之间的边反向,如图4所示。 图4 2-opt示意图 2)两点交换法是从路径间或路径内随机选择两个客户点,如果交换有效,则交换两个客户点在路径中的位置,即 db+bc+ca 如图5所示。 图5 交换法示意图 3)单点插入法是从路径间或路径内随机一个客户点插入到最佳位置。即 da+ab+bc 如图6所示。 图6 单点插入法示意图 1)初始化参数,种群规模为M,最大迭代次数Tmax,交叉概率Ps和变异概率Pmu,交叉点选择概率Pc,当前迭代次数0。 2)采用变邻域搜索算法对种群进行初始化。 3)计算个体适应度值大小,进行从大到小排序。 4)根据动态精英保留策略和轮盘赌的方式选择个体。 5)根据交叉概率公式决定被选择个体是否进行交叉操作,并根据概率选择交叉方式。 6)若Prand_mu 7)遗传操作完成后,对新生成的染色体进行变邻域搜索,选择合适的调整方法对新染色体进行调整。 8)当前迭代次数加1,判断是否达到最大迭代次数,若没有达到,继续从3)开始执行,否则输出最优结果。 为了验证该算法在求解有容量车辆路径问题的准确性,文中选用20个CVRP的算例进行测试。实验环境:CPU为AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz,内存选取为8 GB,操作系统为64位Windows10,采用整数运算,实验误差定义为 已知最优解为测试数据集提供的最优解。 实验过程对算法参数进行初始化,最大迭代次数Tmax为100,初始种群数量M为10,交叉概率Pcro为0.6,变异概率Pmu为0.1,交叉点个数选择概率Pcro_num为0.7,当前迭代次数0。选取了CVRPLIB数据集中部分算例运行结果如图7所示。 图7 部分实例结果图 由图7可知,改进后的遗传算法无论是在求解准确率,还是在求解速度上都有明显提高。 对每个实例统计20次,CVRP实验结果见表1。 表1 改进遗传算法求解CVRP实验结果 由表1可以看出,当客户节点在50个以内时,可以求出最优解,且平均误差也能保证在1%以内,随着客户节点个数的增加,该算法也能够得到最优解或者接近最优解,且平均误差可以保证在1.8%以内。 在实验环境相同的情况下,为进一步验证算法的准确性,文中与AGGWOA[13]、ISA[14]、VNSS[15]算法进行比较,结果见表2。 表2 混合遗传算法同其他算法比较 由表2可以看出,文中提出的混合遗传算法在求解A类数据集时,无论是在求解最优解还是平均值,都要优于遗传算法与灰狼算法结合的算法AGGWOA和改进后的模拟退火算法ISA,但要弱于改进后的邻域搜索算法。 随着客户节点个数的增加,所有算法的求解能力都有所下降,文中算法的下降速度要低于其他算法。 在传统遗传算法的基础上进行了改进,通过采用变邻域搜索算法完成对种群的初始化,并将分组策略和轮盘赌相结合进行染色体的选择,避免了算法陷入局部最优。将单点交叉和两点交叉结合的交叉方式在算法后期仍然能够保证种群的多样性,文中通过CVRP的案例,与其他启发式算法进行比较,无论是在求解效率和求解质量上都有明显提高,对今后车辆调度问题的研究有很大帮助。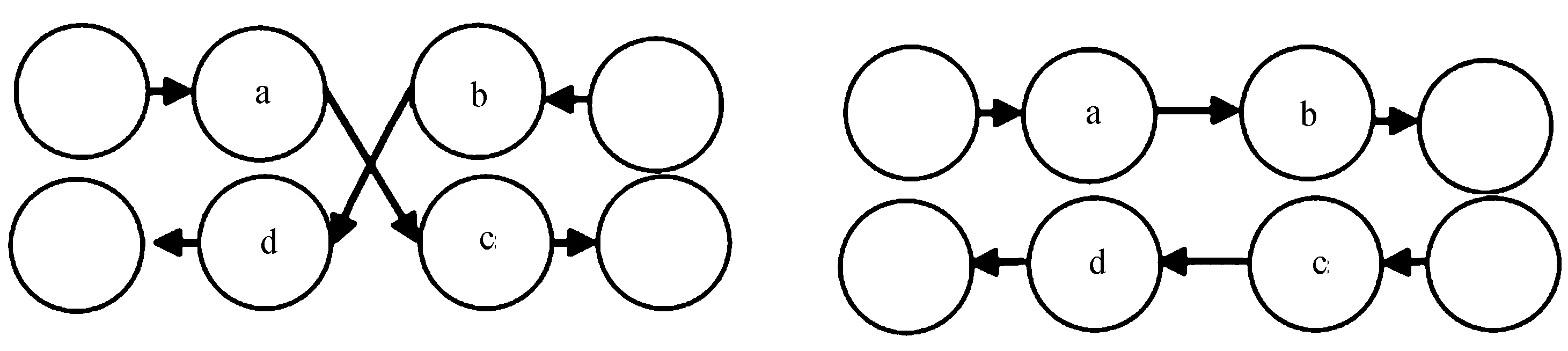


2.8 算法流程
3 实验结果
3.1 测试用例与环境

3.2 数据分析


4 结 语

