河南省财政收入影响因素分析

刘 怡, 徐平峰

(长春工业大学 数学与统计学院, 吉林 长春 130012)

0 引 言

财政是实行宏观经济调控的重要杠杆,探究地方财政收入发展变化情况,对政府而言,能够帮助其进行合理的财政收支计划安排和统筹相应的预算,更好地服务经济发展;对社会而言,能够促进社会公平、稳定社会经济,并提高人民生活幸福程度。因此,对财政收入的研究具有十分重要的意义。

一些学者使用回归方法对财政收入的影响因素进行研究,李波等[1]针对我国财政收入可能存在的影响因素,基于LS多元线性回归模型预测中国财政收入未来增长趋势。杨涵等[2]通过多元线性回归方法分析了河北省财政收入影响因素。江星等[3]通过计量经济学相关知识,就安徽省财政收入及其相关经济数据使用Eviews软件建立多元回归模型进行计量经济学分析,并提出相关建议。更多的学者使用机器学习的方法建立模型,进而对影响因素进行探究。倪杰[4]首先利用统计学中的变量筛选方法与机器学习中的变量筛选方法分别对初步选择的21个自变量进行筛选,然后利用自适应Lasso-半参数模型进行后续的预测。刘倩[5]为实现江浙沪财政收入的预测,用神经网络模型来拟合财政收入与影响因子之间复杂的非线性关系,建立LASSO-RBF、岭回归-RBF、弹性网-RBF三个组合预测模型,为江浙沪未来的经济发展提供了重要启示。连强[6]建立了兼具灰色GM(1,1)模型和多元线性回归模型优点的河南省财政收入多因素灰色模型,模型预测结果显示,河南省未来几年财政收入将持续大幅增加。卢荣伟等[7]利用Adaptive-Lasso变量选择方法识别影响财政收入的关键因素,在此基础上,建立改进的灰色神经网络预测模型,对南宁市财政收入值进行预测。

1 数据选取

为预测河南省财政收入变化趋势,选取1998-2020年间的数据,根据相关资料,选取15个影响财政收入(Y)的主要因素:X1为就业人员数;X2为城镇非私营单位就业人员年平均工资;X3为社会消费品零售总额;X4为城镇居民人均可支配收入;X5为城镇居民人均消费性支出;X6为年末总人口;X7为全社会固定资产投资增速;X8为地区生产总值;X9为第一产业增加值,第一产业是我国的基础产业;X10为第二产业增加值,第二产业是指工业和建筑业;X11为第三产业增加值,第三产业是指流通和服务行业;X12为税收收入;X13为进出口总额;X14为居民消费水平总指数;X15为居民消费水平。

相关数据来源于河南省统计年鉴[8]。

1.1 描述性分析

首先对河南省地方财政收入及影响因素的原始数据进行描述性分析,给出了变量数据的最小值、最大值、25%临界值、中位数、75%临界值和均值6个主要统计量结果,见表1。

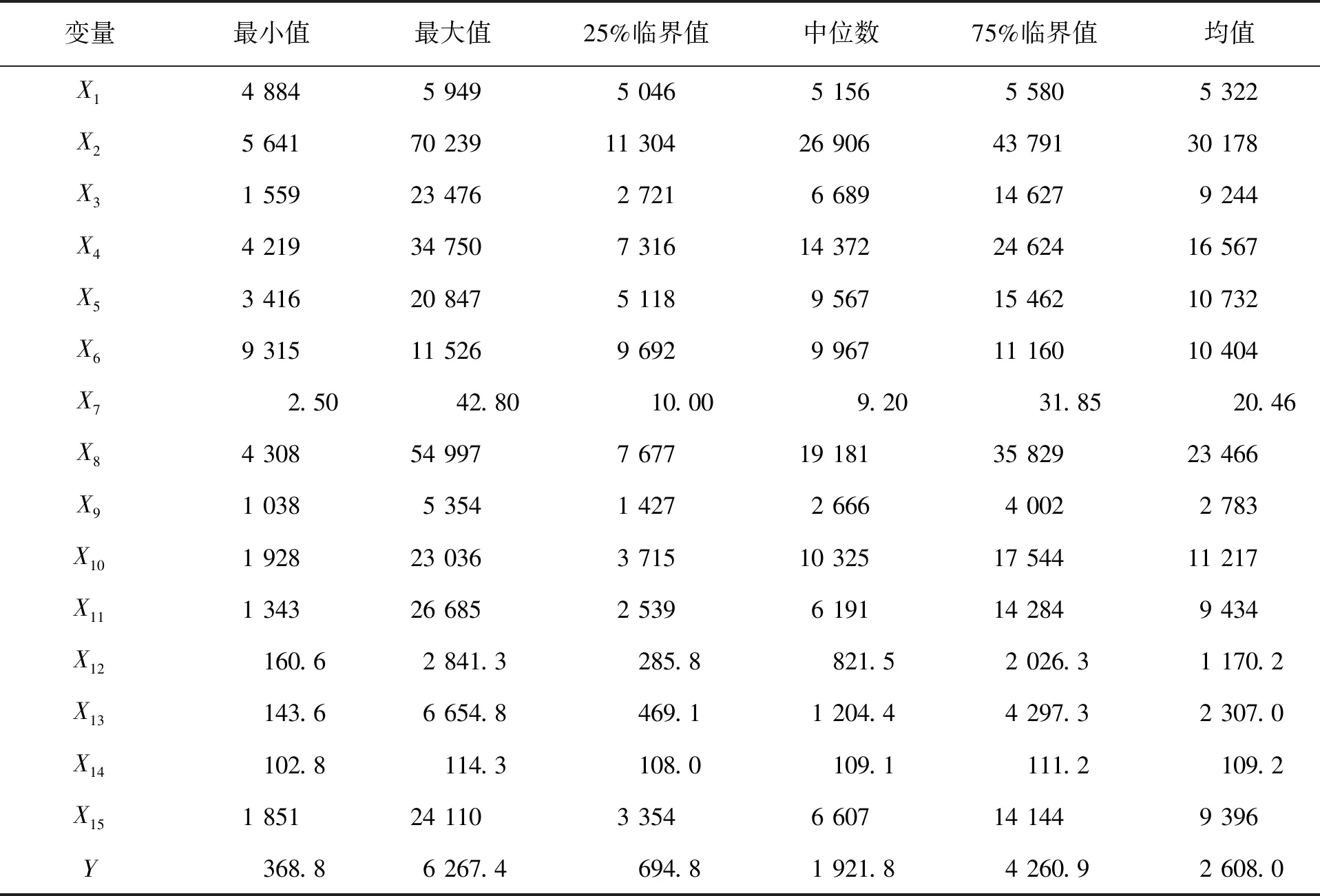
表1 描述性统计分析结果

由描述性统计分析结果可以看出,从1998-2020年,河南省财政收入翻了20多倍,从1998年河南发生特大洪水,经济遭受重创,到2021年河南在全国率先开展大规模高标准农田建设,党的十八大以来,河南瞄准高质量发展主攻方向,三大产业协同向中高端迈进,推进河南产业体系加速形成,再到最后的财政收入飞速上升,这中间既离不开国家层面的有效引导和支持,也离不开地方政府的统筹规划。除此之外,在众多影响因素中,城镇非私营单位就业人员年平均工资(X2),社会消费品零售总额(X3),地区生产总值(X8),第二产业增加值(X10),第三产业增加值(X11),税收收入(X12),进出口总额(X13),居民消费水平(X15)也均翻了10倍以上,财政收入激增的背后是人民生活水平的提高,地方产业水平的提升,以及消费投资的不断增长,各个环节之间相辅相成,共同促进了河南省朝着更富、更强、更美的方向迈进。

1.2 相关性分析

通过定性分析对影响河南省地方财政收入的因素进行了初步探讨,但仍然需要对数据进行定量的相关分析,主要利用简单的相关系数作初步分析,绘制相互两个变量之间的热力图,如图1所示。

图1 两个变量之间的热力图

由图1结果可以得出,全社会固定资产投资增速(X7)与财政收入以及其余变量之间的相关系数均在[-0.4,0]之间,任意两个变量间的相关性也很小,且变量之间是负相关关系。居民消费水平总指数(X14)与财政收入以及其余变量之间的相关系数也均在[-0.4,0]之间,任意两个变量间的相关性很小,同样,变量之间是负相关关系。这说明二者变量与河南省地方财政收入之间的关系不够强,而其余因素变量的相关系数较高,与河南省地方财政收入都表现出高度的相关关系。

在最开始进行变量选择时,往往选择尽可能多的变量,以使得模型预测更加准确,预测结果更具有可靠性与准确性。但若变量选择得过多或者不合理,也会增加预测成本,而变量之间也可能存在多重共线性,导致预测结果不尽如人意,所以,变量的选取至关重要,需要采用适合的方法进行变量的筛选。

2 多元线性回归

2.1 逐步回归变量选择结果

作为经典的统计方法之一,多元线性回归是将两个或两个以上变量的集合联系起来的最常用的统计技术。引入多元线性回归模型探究因变量(Y)和各个自变量之间的关系,由于选取的15个自变量之间一定存在着高度的多重共线性问题,若直接进行拟合,则无法选出相关性较强的变量,模型方程也会因为存在高度的多重共线性而存在问题,因此选用逐步回归的方法先进行变量选择,再使用最小二乘估计来求得回归系数,得出预测模型。逐步回归选取的变量结果及对应的回归系数和检验P值见表2。

表2 逐步回归变量选择结果

由表2可以看出,逐步回归选择出来的变量是:城镇居民人均可支配收入(X4)、第二产业增加值(X10)、第三产业增加值(X11)、税收收入(X12)、进出口总额(X13)。其中,城镇居民人均可支配收入(X4)所对应的回归系数为-0.034 470,且检验P值大于0.01,没有通过检验;除此之外,其余4个变量均为正值,且P值检验的结果都小于0.01,通过了显著性检验。

2.2 回归诊断

回归诊断结果如图2所示。

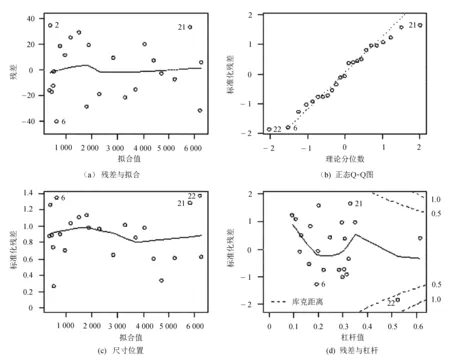
图2 回归诊断结果

图2(a)用于验证因变量与自变量是否线性相关,所有的点应该均匀地落在[-2,2]之间,而图中的点落在了[-40,40]之间,远超合理范围,所以认为该模型不满足线性假设。图2(b)用于判断因变量是否呈正态分布,当自变量值固定时,若因变量满足正态假设,则残差值也应该是一个均值为0的正态分布,正态Q-Q图是在正态分布情况下的标准化残差概率图,可以看出图上的点基本都落在呈45°角的直线上,满足正态假设。图2(c)用于验证同方差性,可以看出水平线周围的点在前半部分更密集,在后半部分更稀疏,并没有十分均匀地随机分布,所以认为该模型不满足同方差假设。图2(d)用于判断是否存在离群点、高杠杆点和强影响点,通过Cook可以看出,存在Cook距离大于0.3的点,即有强影响点。

综上所述,在建立多元线性回归模型中,筛选出来的变量X4不通过显著性检验,整个模型不通过线性检验和同方差检验,并且存在强影响点,所以认为该模型的建立不合理,接下来将使用其他方法来建立新的模型。

3 岭回归

3.1 模型实现

岭回归分析法是通过牺牲估计的无偏性来换取估计方差的大幅减小,以修正最小二乘法在多重共线情况下的估计效果[9]。岭回归与多元线性回归的最大不同是,多元线性回归对变量使用最小二乘估计的方法求得回归系数,而岭回归是在最小二乘估计的基础上加了一个L2惩罚项,其中包括一个岭回归参数k。

建立岭回归模型的关键点在于确定好岭回归参数,这个岭回归参数称为最佳岭回归参数,它是通过岭迹图来判断的。首先,对样本数据进行标准化处理,然后画出岭迹图,根据迹图确定最佳岭回归参数k,结果如图3所示。

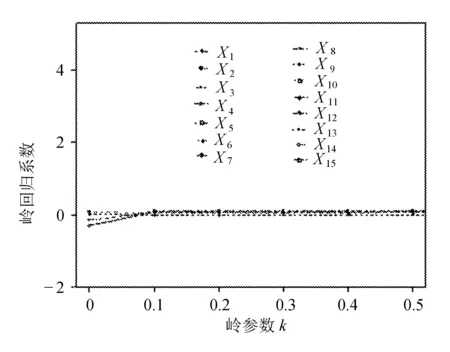
图3 岭迹图

图3中横轴表示岭参数k,纵轴表示岭回归系数,取不同的k值,对应不同的岭回归系数,一般k的取值范围是0到1,当k取0时,对应的岭回归系数就是普通线性回归中通过最小二乘估计得到的回归系数,随着k的增大,模型对共线性处理的效果越来越好,但是拟合精度会有所下降,因此必须找好平衡点,确定出最佳岭回归参数。

综上所述,根据最佳岭回归参数的选取原则,即在岭轨迹变化趋于稳定时选取其最小值,最终决定选择最佳岭回归参数的取值为0.1。

通过R软件得出在最佳岭回归参数确定下的模型方程的各自变量对应的岭回归系数,见表3。

表3 岭回归变量的回归系数

由于将数据进行了标准化,所以模型中不含截距项。

3.2 模型拟合

得到模型方程后,将数据代入得到每一年份河南省财政收入的估计值,然后与真实值作对比,得到的真实值与拟合值如图4所示。

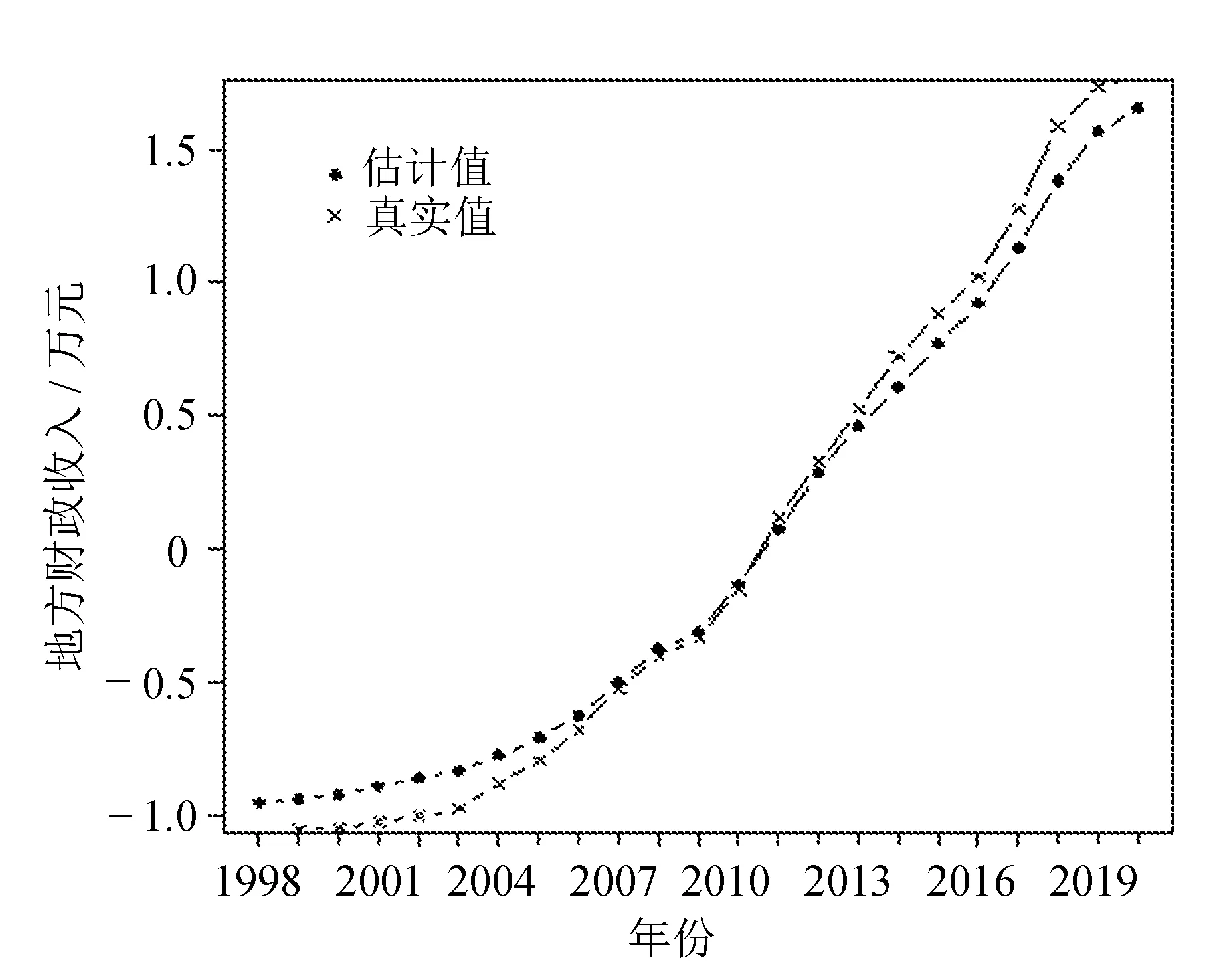
图4 真实值与拟合值(岭回归)

通过图4可以发现,估计值与真实值之间的拟合效果还是不错的,这表明通过岭回归建立的模型方程可以用于实际预测,当给出新一年自变量的取值后,可以拿来预测该年份对应的河南省财政收入的值。

4 自适应Lasso

4.1 自适应Lasso变量选择

Lasso是一种常用的同时估计和变量选择的技术,相对于岭回归方法的优点在于可以做变量选择,Adaptive-Lasso方法是在进行运算的过程中将不同的惩罚给予不同的变量,变量不重要,惩罚就大;变量越重要,惩罚越小[10]。因此可以很容易地选择重要的变量,而不重要的变量就会被剔除,从而达到变量选择的目的,而同时也能对变量进行参数估计,这就在根本上改进了Lasso方法,Adaptive-Lasso 方法在弥补其不足的基础上具有更广泛的应用前景[11]。

通过R软件调用Lasso包,得到的选择变量结果及系数见表4。

表4 自适应Lasso的变量选择结果

由表4可以发现,某些自变量的系数被压缩成0,可以将这些被压缩成0的系数所对应的自变量从模型中剔除出去,将剩余的变量纳入到模型中。地区生产总值与第一产业、第二产业、第三产业齐头并进,共同决定和衡量河南省地区的财政收入水平。

4.2 灰色神经网络检验

灰色预测检验一般有残差检验、关联度检验和后验差检验。这里采用后验差检验,根据后验差检验判别标准表检验各变量预测好坏。当计算结果C<0.35时,表示模型精度好;当0.350.65时,表示模型精度不合格。针对自适应Lasso选取的变量计算C值,得出结果见表5。

由表5结果发现,通过自适应Lasso选取的4个变量中,针对X8(地区生产总值),X9(第一产业增加值),X11(第三产业增加值)计算出的C值均小于0.35,所以对预测模型的精度是好的,只有变量X10(第二产业增加值)计算出的C值是0.469,大于0.35,但是依旧小于0.50,可以判断是合格的。

综上所述,通过灰色模型检验判断,可以将通过自适应Lasso筛选出来的变量全部放到模型中。

4.3 模型拟合

通过自适应Lasso模型得出每一年的河南省财政收入分析的估计值,同样将其与真实值作对比,得到拟合结果如图5所示。

图5 真实值与拟合值(自适应Lasso)

从图5可以看出,通过神经预测模型得到各期的估计值与真实值之间很接近,两条直线几乎重叠,表明拟合效果较好。

5 模型比较

单从两条曲线的拟合度来看,自适应Lasso拟合的结果会比岭回归拟合的结果更好,但为了进一步说明,文中通过RMSE准则来判断,即计算两个模型的均方根误差,结果见表6。

表6 模型比较

通过计算结果发现,使用自适应Lasso进行变量选取来建立模型,得到模型结果的均方根误差要小得多。

综上所述,在针对河南省财政收入的分析所建立的模型中,最终选择了后者。