交叉熵蒙特卡洛法在含风电场电力系统小扰动稳定性评估中的应用

蒋 慧

(淮南联合大学 智能制造学院, 安徽 淮南 232038)

0 引 言

风电作为最具有开发潜力的可再生能源在世界范围内迅速发展。根据全球风能理事会《2022年全球风能报告》发布的数据,2021年,全球新增风电装机容量93.6 GW,累计风电装机容量达837 GW,同比增长12%。2021年,中国风电新增并网装机容量47.57 GW,占全球当年新增装机容量的50.91%。截至2022年底,中国风电累计装机容量395.6 GW,占全球风电总装机容量三分之一以上。随着风电场装机规模的不断增加,产生的风功率波动致使风电输出功率不稳定,甚至造成风力发电机组脱网,特别是随着渗透率的不断提升,风电功率随机性和波动性被视为随机扰动注入电网,从而对电网的稳定性产生影响[1-2]。

电力系统小扰动稳定性分析方法主要包括确定分析法和概率法两类,目前多采用概率分析方法[2-4],随机理论中的随机响应面法、点估计法、蒙特卡洛法相继被应用于分析随机电力系统的随机小扰动稳定性问题[5-9]。文献[5]考虑风速相关性的风电场群模型,运用随机响应面法分析了系统的小扰动稳定性。文献[6]将风速作为威布尔分布的随机变量,基于2m+1点估计法和Cornish Fisher展开法,采用正交变换技术处理风电场之间的相关性,提出一种对具有相关风源的电力系统进行小信号稳定性分析的概率方法。其中,由于蒙特卡洛仿真(Monte Carlo Simulation, MCS)对系统输入概率函数模型无特殊要求,且收敛性与系统维数无关,所以被广泛应用。文献[7]将系统的发电方式、负荷水平和网络拓扑的不确定性作为随机扰动,基于蒙特卡洛状态抽样方法,通过分析系统特征参数的概率特性和失稳概率研究了电力系统小扰动概率稳定问题。文献[8]针对小扰动稳定概率评估问题,利用特征值分析法结合蒙特卡洛模拟法对系统进行评估。通过建立负荷水平和网络拓扑随机变量的概率模型和小干扰稳定概率指标,对新英格兰系统进行了评估。但是传统的蒙特卡洛算法在计算精度和计算时间两个方面存在矛盾,为了克服这一矛盾,常采用分层抽样法、重要抽样法、等分散抽样法、拉丁超立方抽样法等减方差技术提高收敛速度和仿真效率[9]。其中,重要抽样法最为常用,基于交叉熵的蒙特卡洛法(Cross Entropy Monte Carlo Simulation, CEMCS)作为一种高效的重要抽样法,可以克服传统蒙特卡洛法对稀有时间的不敏感问题,引入到电力系统可靠性分析中,有效地克服了传统蒙特卡洛仿真收敛满的缺点[10-11]。文献[10]提出一种基于交叉熵的蒙特卡洛法,并将其应用于发电系统充裕度评估中,使用重要抽样密度函数,通过求解最优问题获得该函数的最优参数,从而提高传统蒙特卡洛法的抽样效率。文献[11]提出一种计及多状态离散型和连续型随机变量的蒙特卡洛扩展交叉熵法,融合预抽样阶段和最优抽样阶段的样本信息得到综合可靠性指标,进一步提升了电网可靠性评估扩展交叉熵法的计算效率。

文中将风电功率波动和负荷变化作为随机小扰动源,构建基于特征值的小扰动稳定性概率指标,通过交叉熵非序贯蒙特卡洛法对系统小扰动稳定性进行仿真。

1 小扰动稳定性概率指标

小扰动稳定分析即在系统稳定运行点时受到随机小干扰后的系统稳定性。

综合文献[3-8,12]对基于特征值的小扰动稳定性进行论述。

设电力系统描述一阶微分-代数方程组为

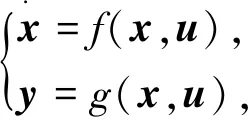
(1)

式中:x----系统状态向量;

u----系统输入向量;

y----系统输出向量。

在稳定运行点(x0,y0)处对上式进行线性化可得

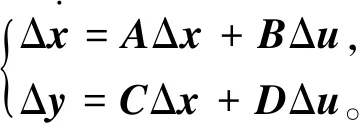
(2)

当零输入状态时,式(2)变换为

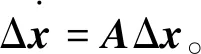
(3)

其特征方程为

|λI-A|=0。

(4)

特征方程的每个解为共轭复数

λi=σi±jωi,

(5)

式中:σi----特征值的实部,反映了阻尼振荡模式;

ωi----振荡频率,ωi=2πfi。

由于阻尼比与特征值存在以下关系,

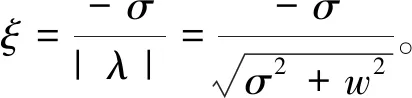
(6)

可知阻尼比和特征值的实部互为异号,根据李雅普诺夫稳定性第一定理可知,状态矩阵A的特征值有负实部,则系统小扰动稳定性,同时,在电力系统中,阻尼比反应的是系统振荡模式,综合两个参数的关系以及系统稳定状态见表1。

表1 小扰动稳定性对照表

由表1可知,阻尼比小于零为系统小扰动失稳的条件,即小扰动失稳指数(Index of Small Signal Instability, ISSI)为

(7)

式中:f(ξ)----阻尼比ξ的概率密度函数。

当ISSI>0时,系统不稳定。

实际情况下,只有当ξ>0.03时,才能保证系统具有足够的低频振荡稳定性,所以,当ξ∈(0,0.03)时,属于弱阻尼振荡模式,存在不稳定风险,确定不稳定风险指标,

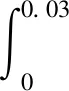
(8)

当IR>0时,存在不稳定风险。

2 交叉熵非序贯蒙特卡洛算法

2.1 非序贯蒙特卡洛法

非序贯蒙特卡洛法是一种大量随机试验法,在电力系统稳定性分析应用中,非序贯蒙特卡洛法不考虑故障时间和维修时间,主要采用按照某种概率密度函数随机抽样系统各元件的状态,继而组合成系统的状态,通过系统分析和稳定性判定[7-8]。

设变量x的期望值μ=E(x),x按照某种概率密度分布函数随机抽样获得互相独立的样本空间为x=(x1,x2,…,xN),计算平均值为

(9)

根据大数定律可知

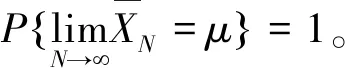
(10)

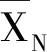
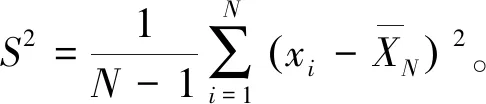
(11)

由中心极限定律可知,随着样本数N的增加,样本均值的概率分布趋于正态分布N(μ,δ2),即样本均值在期望值附近的概率最大。则样本均值方差为

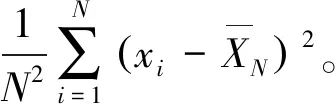
(12)

定义方差系数β作为收敛精度和条件为

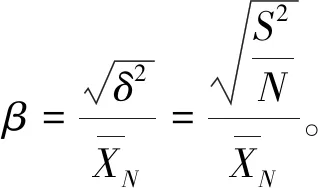
(13)

2.2 交叉熵算法

在大多数情况下,小扰动稳定指标ISSI=P{ξ<0}属于稀有事件的概率,采用传统非序贯蒙特卡洛算法进行无偏估计需要大量样本才能获得足够的计算精度。

交叉熵法作为重要抽样法的一种,其核心是构造一个重要抽样概率密度函数g(x)代替原概率密度函数f(x),计算均值与期望值的距离,以交叉熵距离最小为收敛依据,表示g(x)与最优gopt(x)越相似,g(x)具体构造过程如下[9-11]：

理论上,系统失稳指标的期望值为

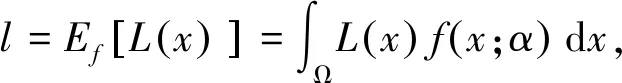
(14)

式中:f(x;α)----随机抽样概率密度函数;

L(x)----状态变量x对应的系统失稳测度函数,满足以下关系:

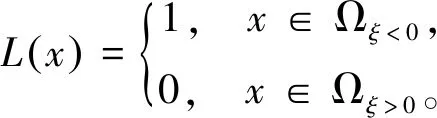
(15)

构造的重要抽样密度分布函数g(x;ν)需满足,

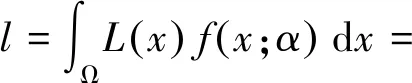
Eg[L(x)W(x;α,ν)],

(16)

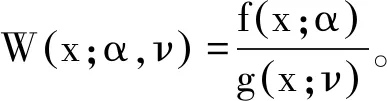
则式(16)的无偏估计为

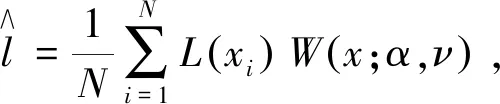
(17)

式中:xi----通过概率密度函数g(x;ν)随机抽取的独立同分布样本。

(18)

然而,实际值l是未知量,无法直接得到最优重要抽样密度函数,因此在寻优阶段,通过迭代减小待更新的重要抽样概率密度函数g(x;ν)和理论上最优的重要抽样概率密度函数gopt(x;ν)的交叉熵来寻找到近似最优的重要抽样概率密度函数。具体为

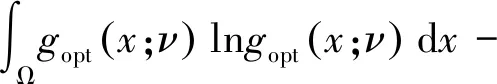
(19)

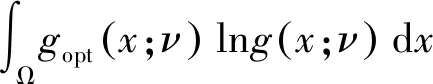
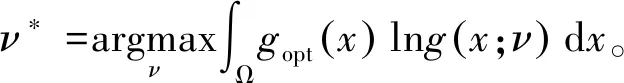
(20)

将式(18)代入式(20)可得

(21)

在重要抽样概率密度的交叉熵寻优阶段,按照式(20)进行随机抽样,式(17)进行小扰动失稳指标的无偏估计。

3 基于交叉熵蒙特卡洛的含风电场电力系统小扰动失稳判定

通过上述分析可知,基于交叉熵蒙特卡洛算法的核心是构造以交叉熵距离最小为依据构造重要抽样概率密度函数g(x)替代原初始抽样概率密度函数f(x),则文中的随机小扰动考虑风电功率波动和负荷变化,两者的初始随机抽样概率密度函数构造有以下几点。

3.1 风电功率随机抽样

考虑因风速随机波动引起风电功率输出随机波动作为随机小扰动。由于双参数Weibull分布的曲线形状与现实状况很匹配,被广泛用来描述风速的分布。风速波动可以采用双参数Weibull分布模拟风速条件概率密度为[13]

(22)

式中:v----风速;

k----形状系数;

c----尺度系数。

风力发电机组一般工作在停车、最大风能跟踪和恒功率输出三个阶段。为了简化计算,风力发电机在不同风速下的有功输出采用近似功率曲线直接转换风速值的方法进行计算,近似计算模型为[14]

(23)

式中:ν、νin、νout、νN、PN----分别为风力发电机的实时、切入、切出、额定风速以及额定功率。

综合式(1)和式(2)可得每台发电机的风电有功输出的抽样值。考虑同一风电场的风速基本相同,将每台发电机的有功输出值求和,可得该风电场的有功输出随机抽样值。

3.2 负荷变化随机抽样

实际系统中节点负荷是一个时刻波动的不确定变量,负荷的变化对系统潮流影响比较大,而电力系统小扰动稳定与网络潮流的初始解有关,因此在小干扰稳定评估中负荷随机性越大,系统的稳定性也就越差。

节点负荷变化的随机性也是影响电力系统小干扰稳定的主要因素之一,所以文中将负荷变化作为随机小扰动。负荷功率概率模型一般采用服从正态分布的概率密度函数进行模拟,

(24)

式中:u----负荷功率的期望值,取统计数据的均值;

σ2----方差,取均值的2%。

3.3 小扰动失稳判定计算流程

设定初始抽样的样本数目Nk,收敛精度γ,按照以收敛精度结束仿真的条件,得出基于交叉熵蒙特卡洛的含风电场电力系统小扰动概率稳定性判定的具体流程,如图1所示。

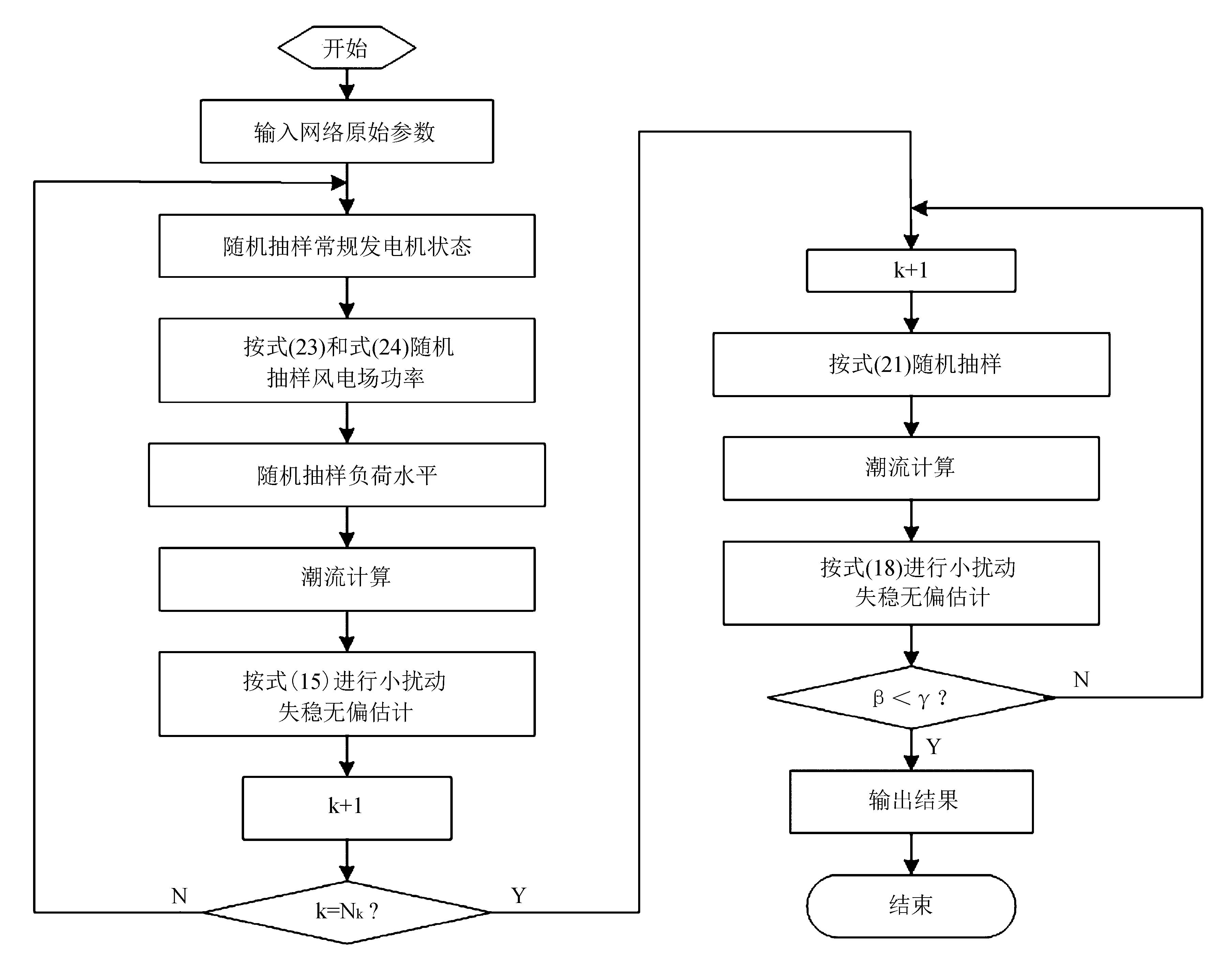
图1 小扰动失稳判定计算流程

4 算例仿真与分析

为了验证本算法风电功率随机波动对系统稳定性影响的有效性,在3机9节点系统的基础上并上一个风电场[15]作为稳定性测试系统,其总装容量为100 MW,其余为300 MW的常规发电机,采用标幺值计算且基准值均取100 MVA,如图2所示。

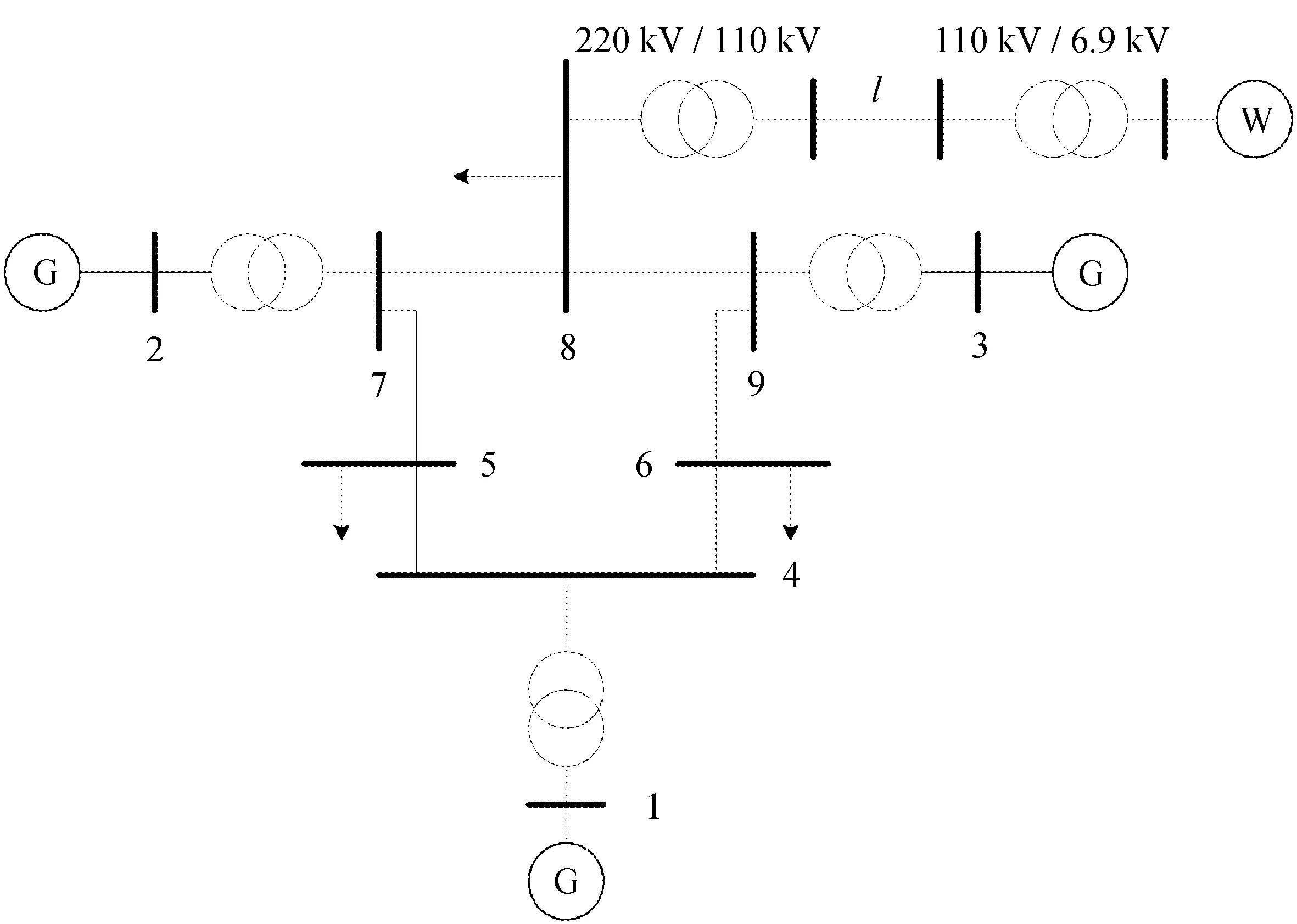
图2 含风电场的3机9节点电力系统

具体Matlab仿真结果与分析见表2。

表2 各常规发电机有功输出概率模型

两台常规发电机有功输出均采用表2中降额概率模型,输电线路采用两状态概率模型。设定切入风速、额定风速以及切除风速分别为3.5 m/s,13 m/s和30 m/s,按照式(22)和式(24)分别对风速和负荷波动进行随机抽样。特征值采用QR算法,潮流计算采用牛顿拉夫算法。

通过风速随机抽样概率密度函数计算得出风电功率抽样的直方图及核密度估计如图3所示。

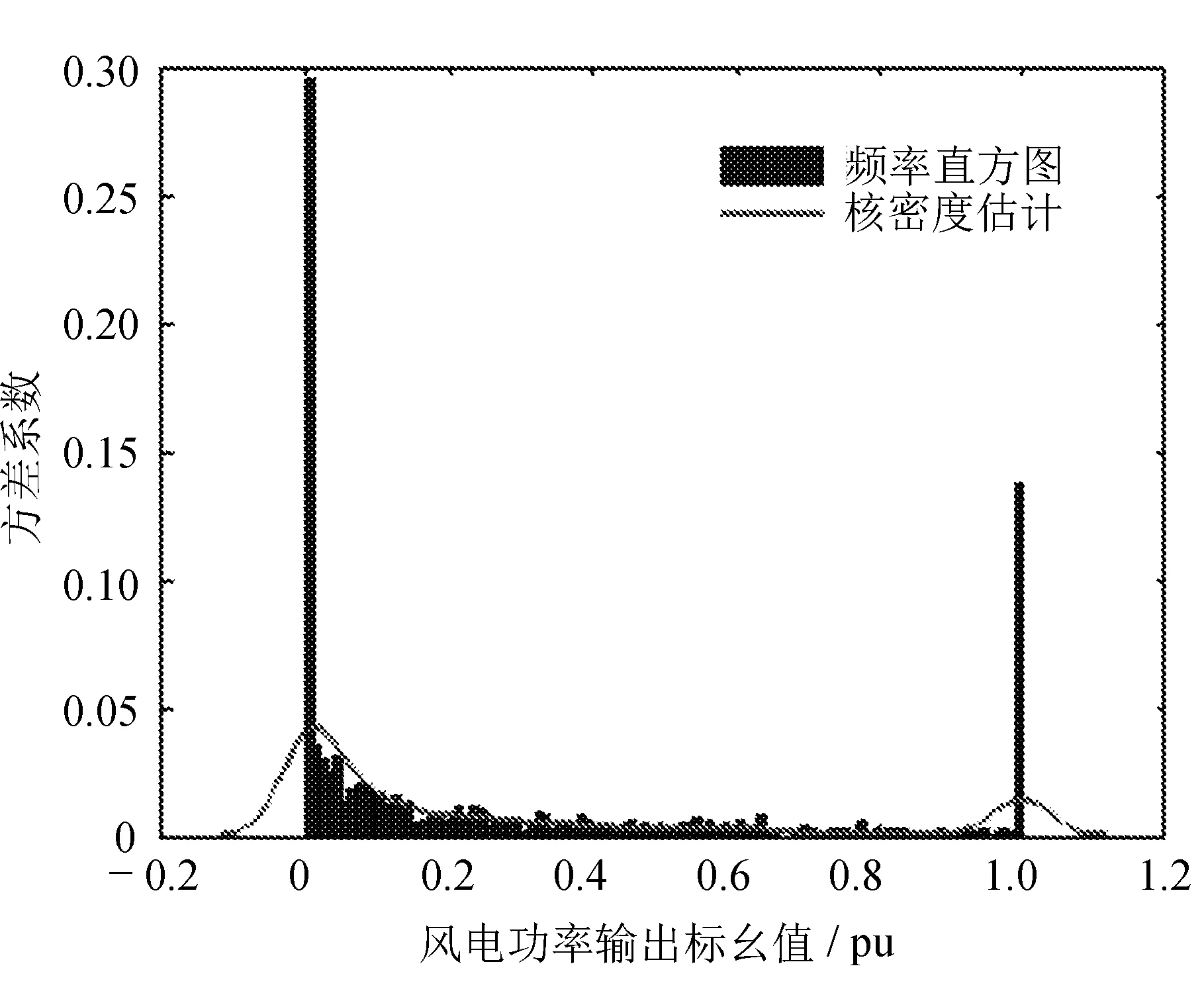
图3 风电输出功率概率直方图

从图3可以看出,风电场零功率输出和满额输出的概率最大,且风电场的功率输出多集中在0.2～0.4 pu之间,能起到随机小扰动的作用。

CEMCS与MCS在小扰动失稳指数(ISSI)和不同收敛精度下的结果见表3。

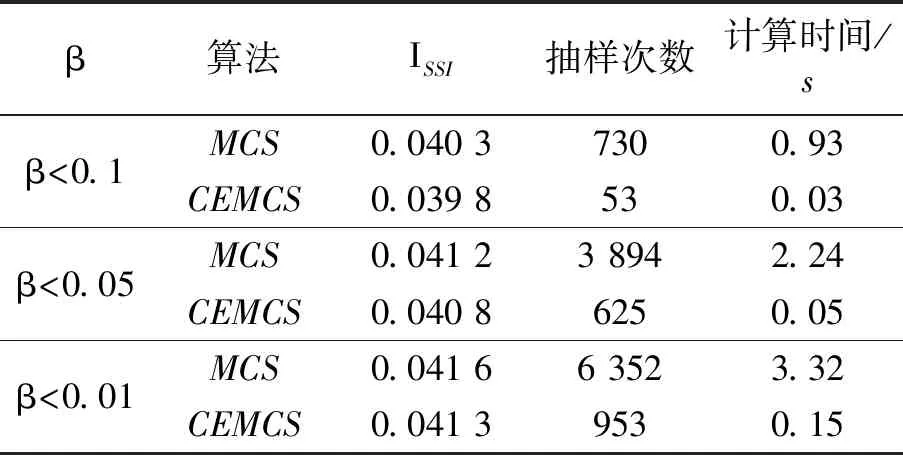
表3 小扰动失稳指数计算及仿真性能表

由表3可知,随着设定方差系数的减小,两个算法计算的小扰动失稳指数均在减小,说明ISSI的计算精度都有所提高,且CEMCS算法的计算精度略高于MCS算法。随着收敛方差系数的减小,传统MCS算法需要大量的抽样次数才可以获得相应的ISSI计算精度,而CEMCS算法的抽样次数和计算时间变化不大。横向比较可知,同一方差系数下,CEMCS算法的抽样次数和计算时间均优于MCS,达到减方差的效果。

设定抽样次数为1 000次,CEMCS和MCS在此抽样次数下的小扰动失稳指标及其方差系数收敛过程分别如图4和图5所示。

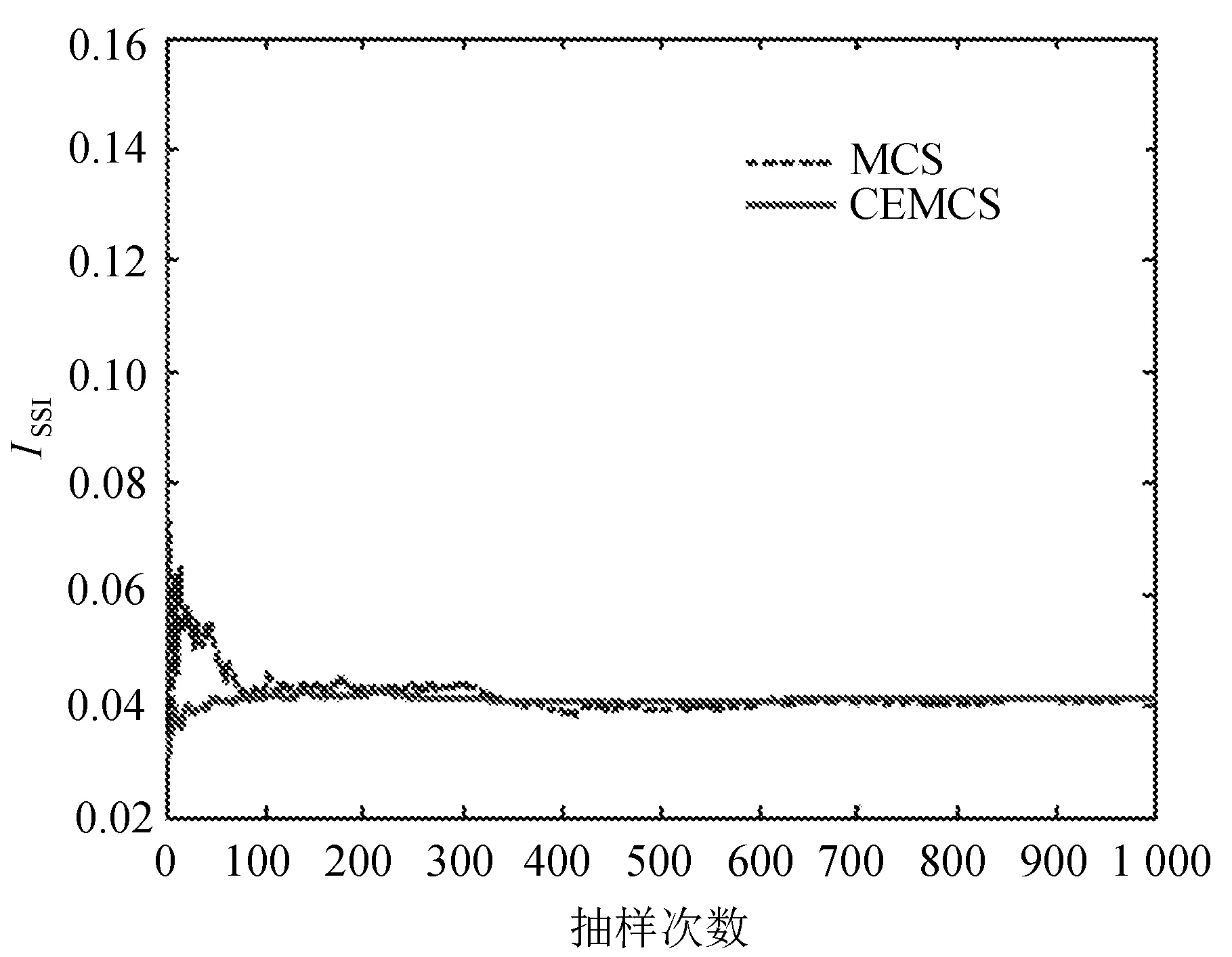
图4 小扰动失稳指标收敛过程

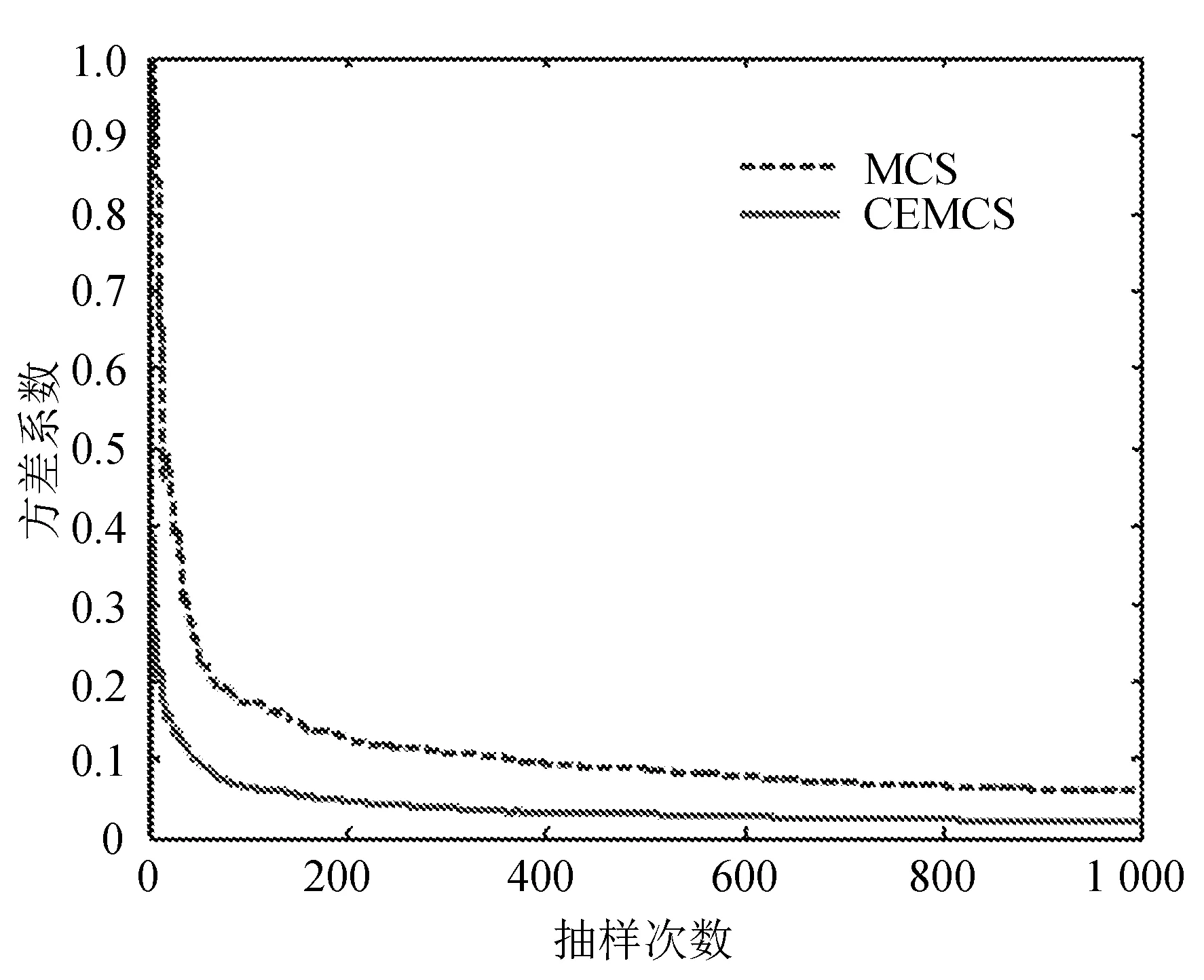
图5 小扰动失稳指标方差系数收敛过程

从图4可以看出,MCS得到的小扰动失稳指标在抽样400次以内的波动非常大,而CEMCS得到小扰动失稳指标快速趋于平稳。图5中CEMCS的方差系数最小值是0.017,而MCS的方差系数最小值为0.081。由此可知,在相同的抽样次数下,CEMCS的方差系数小于MCS的方差系数,即在收敛精度方面CEMCS较优。在收敛速度方面,CEMCS在抽样400次左右已趋于最优值,而传统算法近1 000次迭代才达到最优值。

5 结 语

将风速引起的风电功率波动和负荷波动作为随机扰动源,利用特征值时域分析法确定小扰动失稳指标,采用非序贯蒙特卡洛分析方法进行概率模拟评估。引入交叉熵降低失效事件的稀疏性,提高蒙特卡洛算法的收敛精度和计算效率。通过算例仿真结果显示,交叉熵非序贯蒙特卡洛算法在小扰动稳定性评估中具有一定的有效性和优越性。