基于多体动力学建模的激光雷达误差研究

苍 鹏, 于 深, 王 震,2*

(1.长春工业大学 机电工程学院, 吉林 长春 130012;2.长春工业大学 工程训练中心, 吉林 长春 130012)

1 多体动力学数学模型

对建筑物的扫描通常采用车载激光雷达进行扫描,该系统主要包含激光雷达和车载平台[1-3]。其中车载平台由基座、控制设备扫描方位的方位轴框系、维持设备横倾角度的横倾轴框系、即时调整设备工作俯仰角度的俯仰轴框系组成[4-7],如图1所示。

图1 车载扫描系统结构简图

将车载平台的基座、三个轴系及激光雷达视为一个多体结构,每个组成部分都视为刚体,并建立刚体坐标系。

在多体动力学理论中需要将系统中所有刚体的参数转换到同一个坐标系再进行测量。在多体动力学模型中,主要有刚体坐标系和整体坐标系[8-9]。整体坐标系不会随时间产生变化。而在刚体坐标系中,每个刚体的平动和转动都会随时间变化而变化。

1.1 约束方程

将车载激光雷达扫描系统简化为n个刚体,建立对应数量的广义坐标来描述此系统,用q表示为

q=[q1,q2,…,qn]T。

(1)

一个完整系统应当具有完整的约束条件,其约束方程的定义域是有界的,可以完整地表达位移、速度等参数。如果约束方程定义域是无界或包含速度参数,则称为不完整约束方程,对应的系统是不完整的。

假设在一个系统中有m1个独立的完整约束,定义一个具有广义坐标的非线性函数

φ(q,t)=0,

其中

φ=(φ1,φ2,…,φm1)T。

然后对式(1)两端求一阶导数,得到该系统速度的约束方程为

(2)

将式(2)两端继续求导,可得系统加速度方程为

(3)

(4)

式中:φq----非线性函数φ对广义坐标q的一阶偏导数,这是一个m1×n阶的矩阵,公式为

(5)

式中:φt----φi对时间t的导数;

φq----m1阶方阵;

φqt----对广义坐标q和时间t求二阶偏导得到的一个矩阵。

假设该系统具有m2个不完整约束为

(6)

不完整约束以及广义速度二者的线性关系为

(7)

(8)

将式(2)、式(6)～式(8)联立,得到车载激光雷达扫描系统总速度和加速度约束方程为

(9)

(10)

(11)

式(10)和式(11)是该系统约束的雅可比矩阵,是一个(m1+m2)×n阶的矩阵,公式为

(12)

(13)

1.2 独立刚体动力学方程

在OXYZ惯性坐标系中,oixiyizi是空间中一个刚体对应的局部坐标系,每个坐标系的圆心Oi与空间中各个刚体的质心Ci重合。用ri表示局部坐标系oixiyizi相对空间中惯性坐标系OXYZ的平动四元数矩阵,θi表示的转动四元数矩阵为

ri=[xiyizi]T,

(14)

θi=[θi0θi1θi2θi3]T,

(15)

则刚体的广义坐标为

(16)

根据柯尼希定理,推导出刚体动能公式为

(17)

式中:m----系统中运动的独立刚体的质量;

r----刚体在惯性坐标系OXYZ中的位置;

ω----刚体运动时的角速度;

I----刚体的惯性张量。

根据欧拉四元数的性质、角速度矢量与欧拉四元数及其导数的关系为

(18)

式中:L----右变换矩阵,公式为

(19)

将式(19)代入式(18),得

(20)

对式(20)进行求导,得

(21)

(22)

(23)

(24)

(25)

(26)

(27)

刚体约束方程为

(28)

系统约束方程对ri和θi两个参数的雅可比矩阵可以表示为

(29)

(30)

根据第一类拉格朗日方程可以推导出

(31)

(32)

式中:φr,φθ----分别代表约束方程对坐标r和坐标θ的雅可比矩阵;

Qr,Qθ----分别为对位置r和θ的刚体产生的广义作用力;

λ----拉格朗日乘子。

综上,可以推导出物体i在四元数空间的动力学方程为

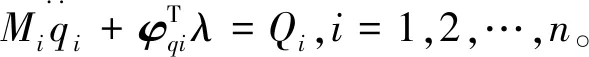
(33)

写成矩阵形式为

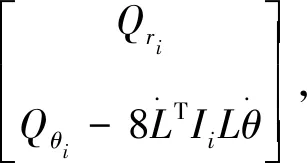
(34)

其中

式中:E3----对角矩阵,对角线上的元素均为常数;

mi----第i个刚体的质量;

1.3 建立多体系统动力学方程

由多个刚体组成的多体系统的通用公式为

(35)

其中

M=diag(M1,M2,…,MN),

(36)

q=[(r1T,θ1T),…,(rNT,θNT)]T,

(37)

φq=[φq1,φq2,…,φqn],

(38)

(39)

将式(33)与该系统约束方程联立,得到多体系统微分方程组为

(40)

在激光雷达扫描多体系统中,主要由车载平台中三个轴系产生回转运动,而各刚体之间没有平移运动。所以车载扫描系统的装配误差表现在车载雷达的安装位置误差、搭载雷达的平台各轴系运动产生的回转误差、不同轴间的垂直度误差和相交度误差。

根据多体运动学原理,建立扫描系统数学模型,其中,规定大地作为这个系统的0体,并设定其为一个低序体。在车载雷达扫描系统中,所有刚体运动都可以归结到0体上,得到系统中任意刚体在大地坐标系中的位置坐标和运动关系。以3和4两个刚体为例,二者的运动关系如图2所示。

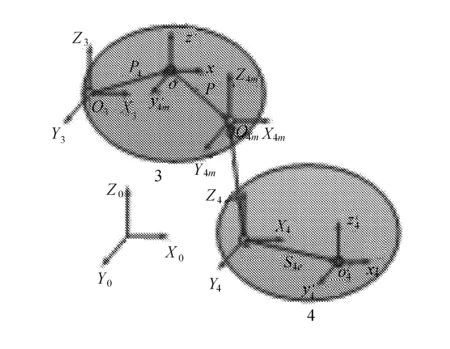
图2 刚体3和刚体4的运动关系示意图

图中符号:

O3----刚体3实际位置;

O4----刚体4实际位置;

O4 m----刚体4运动实际位置;

p4----刚体4理想位置矢量;

p4e----刚体4位置误差矢量;

s4----刚体4运动矢量;

s4e----刚体4运动误差矢量。

通常情况,实现两相邻刚体变换的矩阵为

T=[T]p[T]pe[T]s[T]se,

(41)

式中:[T]p----刚体运动理想位置矢量;

[T]pe----刚体运动位置误差矢量;

[T]s----刚体运动矢量;

[T]se----运动误差矢量。

车载扫描设备在大地坐标系内实际位置为

(42)

2 激光雷达扫描系统误差分析

2.1 车载激光雷达扫描系统几何误差分析

2.1.1 轴系回转误差

车载激光雷达扫描系统有三种回转轴线,即理想、实际、瞬时回转轴线。轴系的回转误差也是由三个方面构成,分别用Δs、Δc0以及Δγ来表示。回转误差还可以被继续分解成纯径向的误差Δx(t)与Δy(t)、轴向发生窜动的误差Δz(t)、倾角回转误差Δα(t)和Δβ(t)。由于工况各异,所以对误差的控制要求也存在差别。

2.1.2 垂直度误差

在空间中有两条相交轴线,它们之间夹角与直角的差异称为垂直度。垂直度主要包含瞬时垂直度和平均垂直度,而后者在工程中更为常用。经过试验可以得到结论,平均垂直度和两个轴的位置及晃动量都对两个轴的轴线之间的瞬时垂直度有较大影响。

2.1.3 相交度误差

两个相互垂直的轴系之间的相交度同样能够影响到扫描精度。用两个轴的轴线在空间中的公垂线的长度表示轴系之间的相交度。这一类误差常常在各个轴的平均回转轴线中间产生。而且运动中的轴的转角位置和一些轻微晃动不会对相交度误差产生影响。相交度误差应当保持小于0.5 mm才能达到建筑物重建工作所需精度。

2.1.4 设备安装误差

为保证激光雷达能够达到扫描精度,每个激光雷达的定位信息初始化标定通常在出厂时便已完成。安装设备时,对雷达的轴线与车载平台中的方位轴的同轴度通常会有一定要求。实际上,即使采用高精度的测量手段,也很难精确地将这种装配误差测量出来。

文中讨论车载扫描系统中的轴系回转误差是系统运动误差的一种,其余三种误差均属于系统几何误差。

2.2 车载激光雷达扫描系统装配误差分析

根据多体动力学原理,在车载扫描系统上建立相应的地面坐标系,将方位轴简化后建立方位轴坐标系,将俯仰轴简化后建立俯仰轴坐标系,横倾轴简化后得到横倾轴坐标系,把激光雷达自身视为一个刚体建立一个坐标系,如图3所示。

图3 各个刚体坐标系及其相互关系示意图

以大地坐标系原点O0为基点,三个方位轴的转角分别为α、β和γ。

2.2.1 大地坐标系

大地坐标系设为坐标系0,其原点是O0,该点在基座所在平面中心。将方位轴坐标系设定为坐标系1,俯仰轴坐标系设为坐标系2,横倾轴坐标系设为坐标系3,激光雷达设定为坐标系4。

2.2.2 方位轴坐标系

2.2.3 俯仰轴坐标系

2.2.4 横倾轴坐标系

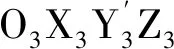
2.2.5 激光雷达自身坐标系

在安装雷达设备时会出现装配误差,这类误差存在于设备的各个自由度中,且各不相同,难以通过技术手段进行消除。

3 建立误差模型

通过建立各个坐标系之间相互转换的模型,可以导出扫描系统中雷达自身所处的坐标系与大地坐标系二者相互变换的转换矩阵为

(43)

(44)

其中

k=1,2,3;l=1,3;m=2;n=1,2,3,4。

如果只考虑设备自身,假设一个矢量r的齐次坐标qr,并将其代入下式,利用插值算法来求出空间中任意点的定位误差。

(45)

由式(45)可以获得系统所需精度,将其代入已经给定的齐次坐标系内计算,可得到激光雷达的整体误差数据。

当qr=[0,0,1,0]T时,如果不计误差角度对系统的影响,则可以不将各转轴产生的回转误差以及设备安装时产生的安装误差考虑在内,指向误差矢量为

(46)

当激光雷达中心点qr=[0,0,0]T时,如果不计算回转轴系的误差,则误差矢量为

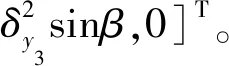
(47)

4 误差仿真分析

将激光雷达扫描系统中所有误差源利用多体动力学原理建立数学模型,评估各个误差源对点云数据精度的影响。将系统的各个刚体坐标统一转换到大地坐标系中,利用控制变量法对每个参数进行分析,使用Matlab软件进行仿真运算,从而获得各系统单方面误差影响。

4.1 垂直度误差的影响

不同垂直度误差对系统定位误差影响如图4所示。

系统指向误差系统指向误差

4.2 相交度误差的影响

相交度对定位误差影响如图5所示。

系统指向误差系统指向误差

4.3 回转误差的影响

系统中倾角误差对定位误差的影响如图6所示。

(a) Δβ2=10′系统指向误差

回转误差对系统的影响与垂直度误差相似,当Δβ2=10′时,定位误差影响见图6(a);图6(b)表示Δγ2=10′时,定位误差受到的影响。通过对比可知,其他倾角造成的误差对系统的影响与Δβ2相比较小。

通过仿真实验结果可以得出,横倾轴与俯仰轴共同决定系统的水平度,是该系统的主要误差来源。而方位轴决定该系统做旋转运动时的回转角度。

5 结 语

根据多体系统动力学原理,将车载扫描系统中基座、横倾轴系、俯仰轴系、方位轴系和激光雷达自身坐标系简化成5个刚体。通过寻找刚体间的关系,将扫描系统简化为一个多体结构,建立系统模型。综合分析多体系统中各种误差的来源,并使用Matlab软件进行仿真运算,得出垂直度、相交度和回转误差对车载扫描系统的误差影响。