右删失数据下OLLMON分布的估计研究

王淑影, 李 洋, 程云飞, 罗琳燕

(长春工业大学 数学与统计学院, 吉林 长春 130012)

0 引 言

随着社会的发展,删失数据逐渐出现在各个领域且成为研究热点,其中右删失数据的模型估计问题备受关注。OLLMON分布与传统的分布函数相比,具有适用范围更为广泛、灵活度更强等优点。

有关寿命数据的统计分析已经发展成为生物医学界的一个重要分支,寿命数据是指各种与时间有关的数据,譬如个体的存活时间、失效时间等。寿命数据一般包括两部分:一是完全数据,即实验个体的生存时间能全部准确观测到的数据;二是删失数据,由于经费和时间等客观条件的限制,获得的不完全数据。

在生存数据分析中,为寿命数据找到合适的生存分布,使得数据与分布函数较好拟合是十分重要的。由于基础理论的不断发展和实践的需求,出现了指数分布、威布尔分布、伽马分布等多种参数寿命模型,然而在用这些经典分布对真实生存数据进行建模时,其效果并不令人满意。为了使模型可以更好地拟合实际数据,学者们尝试在原有的模型中添加新的参数或加入拓展项得到新的模型。Marshall A W等[1]、颜荣芳等[2]、 Gui W H[3]、Braga A S等[4]、Cruz J N D等[5]、李群等[6]、Alizadeh M等[7]、Vasconcelos J C S等[8]将提出的新模型运用到一般数据下,并进行参数推断。随着这些新模型在完全数据下的研究逐渐成熟,Ghitany M E等[9]、Ghitany M E等[10]、Kumar S S等[11]、Calabrese R等[12]、Ke W等[13]开始考虑将这些模型引入到删失数据中。

根据国内外文献综述可以看出,近年来,有大量学者都投入到删失数据下扩展分布的研究中,所以文中探究右删失数据下OLLMON (Odd Log-logistic Marshall-Olkin Normal)分布的相关统计特性是有价值的。OLLMON分布是Vasconcelos J C S[14]在Marshall-Olkin分布与Odd Log-logistic分布基础上拓展出来的新模型,其具有双峰性和非对称性,相较于正态分布、Odd Log-logistic分布与 Marshall-Olkin Normal分布,OLLMON分布更为灵活。OLLMON分布在完整数据下的相关研究已较为成熟,但是删失数据下OLLMON分布的相关研究较少,故文中的探究具有一定的研究意义。

文中针对右删失数据构建了基于OLLMON分布的参数模型,使用极大似然方法给出感兴趣参数θ的估计。并进行了大量数值模拟研究,最后对NCCTG肺癌数据集进行了实例数据分析。

1 右删失数据下OLLMON分布的极大似然估计

对于某感兴趣事件,其生存时间记为Xi(i=1,2,…,n),删失时间为Ci,当Xi≤Ci时,得到精确观测值Xi,当Xi>Ci时,得不到精确观测,则认为变量在Ci处发生了右删失。故在右删失情况下得到实际的观测样本为(Ti,δi),其中

Ti=min(Xi,Ci),

δi=I,Xi≤Ci。

设总体Xi服从参数为μ,σ,ν,τ的OLLMON分布,则其概率密度函数为

{Φ(z)τ+ν[1-Φ(z)]τ}-2,

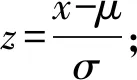
μ,σ----N(μ,σ2)分布参数;

ν,τ----形状参数,ν>0,τ>0;

Φ(·)----标准正态分布函数。

其分布函数与生存函数为:

当ν>0且τ=1时,即得Marshall-Olkin Normal分布;当τ>0且ν=1时,即得Odd Log-logistic Normal分布;当ν=τ=1时,得到N(μ,σ2)分布。

得到右删失数据下的似然函数为

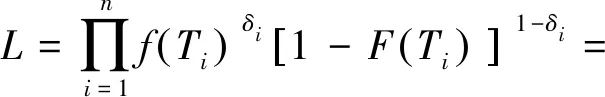
其对数似然函数为

(τ-1)lnΦ(zi)+(τ-1)ln[1-Φ(zi)]-

对上述对数似然函数关于参数μ,σ,ν,τ求一阶偏导数,并令其等于0,得到似然方程,似然方程的解可作为μ,σ,ν,τ的极大似然估计。文中借助R语言stats包中的optim函数得出参数的极大似然估计值。在进行理论标准差求解时,需求出协方差矩阵的估计,文中采用Bootstrap方法,令θ=(μ,σ,ν,τ),首先生成服从OLLMON分布的右删失数据集O,设B是提前设定好的正整数,对于每一个b=1,2,…,B,从删失数据中重复抽样得到B个独立的Bootstrap样本

记

2 数值模拟

为验证分布模型的参数估计效果,采用蒙特卡洛方法进行数值模拟。具体步骤为:

首先,生成n个服从于均匀分布U(0,1)的简单随机样本{Y1,Y2,…,Yn},那么Xi=F-1(Yi),i=1,2,…,n便是服从于OLLMON分布的独立同分布样本;对生存数据进行排序得到X(1),…,X(i),…,X(n),基于删失比Cr确定删失时间点X(m),继而生成n个服从于均匀分布U(X(m)+ε1,X(m)+ε2)的简单随机样本Ci,其中,ε1、ε2均表示任意大于零的极小数,且ε1>ε2,根据Ti=min(Xi,Ci)得到观测变量Ti;定义当Xi≤Ci时,δi=1,当Xi>Ci时,δi=0,这样就产生了n个服从OLLMON分布的右删失数据(Ti,δi)。

将上面步骤重复1 000次,可得到1 000个右删失机制下服从OLLMON分布的样本。将其代入极大似然估计的算法公式,可得到参数的估计值,继而得到偏差(Bias)、理论标准差(ESE)与均方根误差(RMSE)。基于样本量为200和400,μ,σ,ν,τ取不同真值组合所得,模拟结果分别见表1和表2。

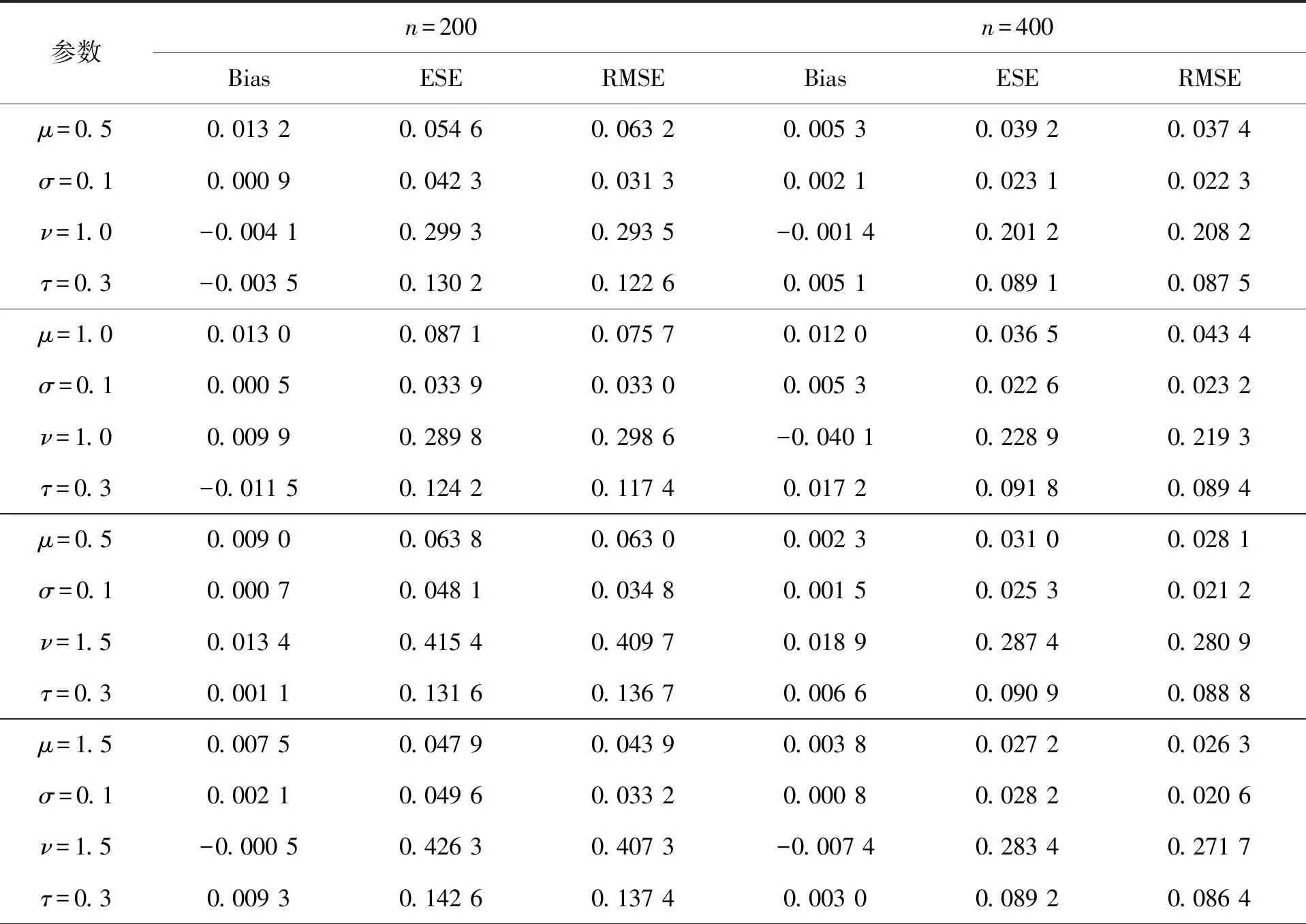
表1 参数估计的Bias、ESE及RMSE (Cr=30%)

表2 参数估计的Bias、ESE及RMSE (Cr=50%)

表1和表2分别给出删失比例Cr为30%和50%时,不同参数组合的模拟结果。从结果可以看出,模拟的参数估计值相较于真值偏差较小,参数的均方根误差趋近于理论标准差,且随着样本数量从200增加到400,估计的偏差和标准差等都一致地显著减小,在一定程度上表明了参数估计量具有相合性。

对比表1和表2可以看出,随着删失比的改变,表2所展示的估计结果相较于表1有些许的波动,出现这种情况的原因是删失数据包含的信息量发生了变化。

3 实例分析

文中将所提方法运用到R语言survival包中的NCCTG肺癌数据集中,此数据集是美国癌症治疗团队NCCTG发布的一则肺癌统计数据报告,其中记录了228例晚期肺癌患者的各项数据,其中包括性别、年龄和各项身体状况表现得分等。

基于OLLMON模型的极大似然估计拟合得到模型的参数估计,同时也展示了MON分布与OLLN分布两种特殊情况的参数估计值,具体见表3。

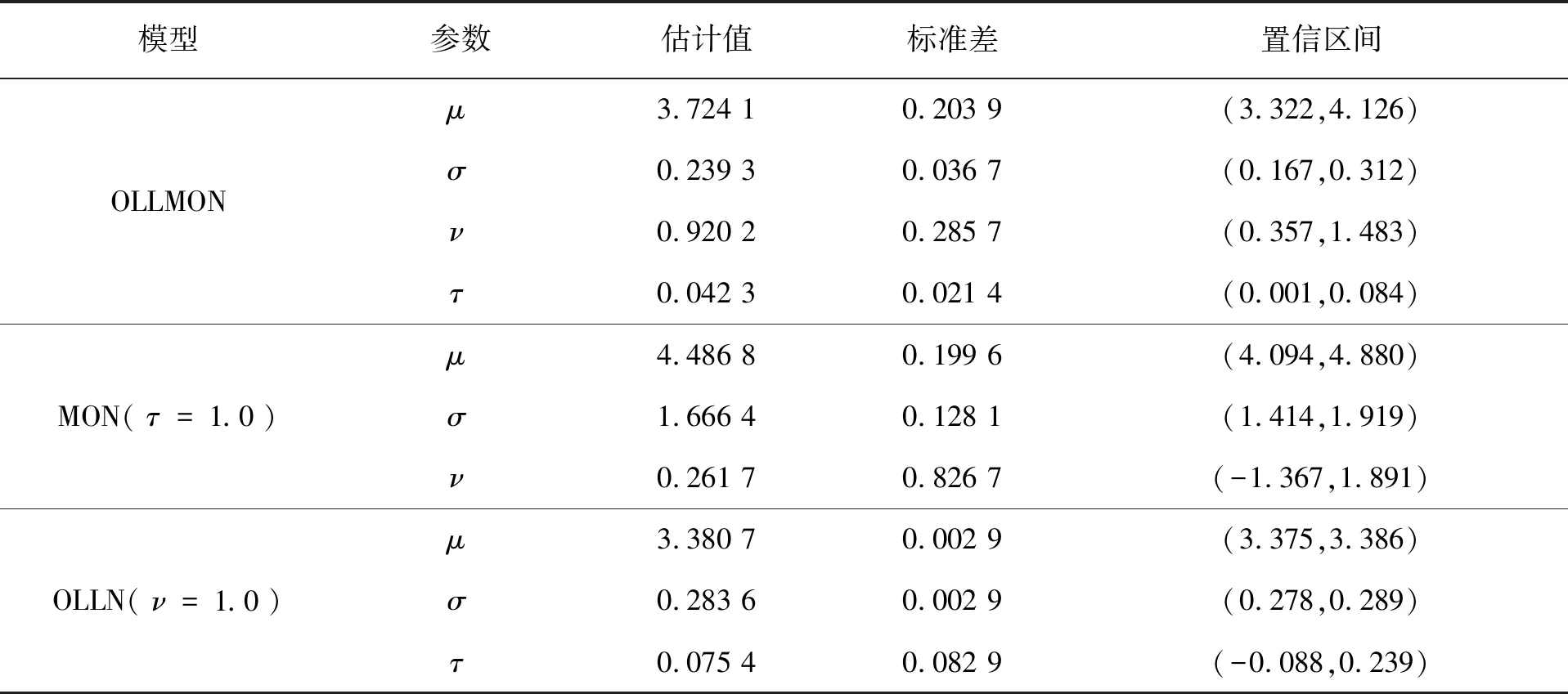
表3 OLLMON、MON与OLLN分布的参数估计结果和相应的标准差与95%置信区间

由上述结果可以看出,OLLMON分布的参数估计值分别为

对于MON分布,参数ν存在不显著现象,对于OLLN分布,参数τ存在不显著现象。而且相较于MON分布、OLLN分布与更加特殊的正态分布,OLLMON分布的适用范围更为广泛,灵活度更强,具有更好的建模能力。此外,表3还展示了估计值的标准差与95%置信区间,根据展示结果可以看出,参数估计结果较为理想。

基于估计结果得到的分布函数和生存函数图如图1所示。

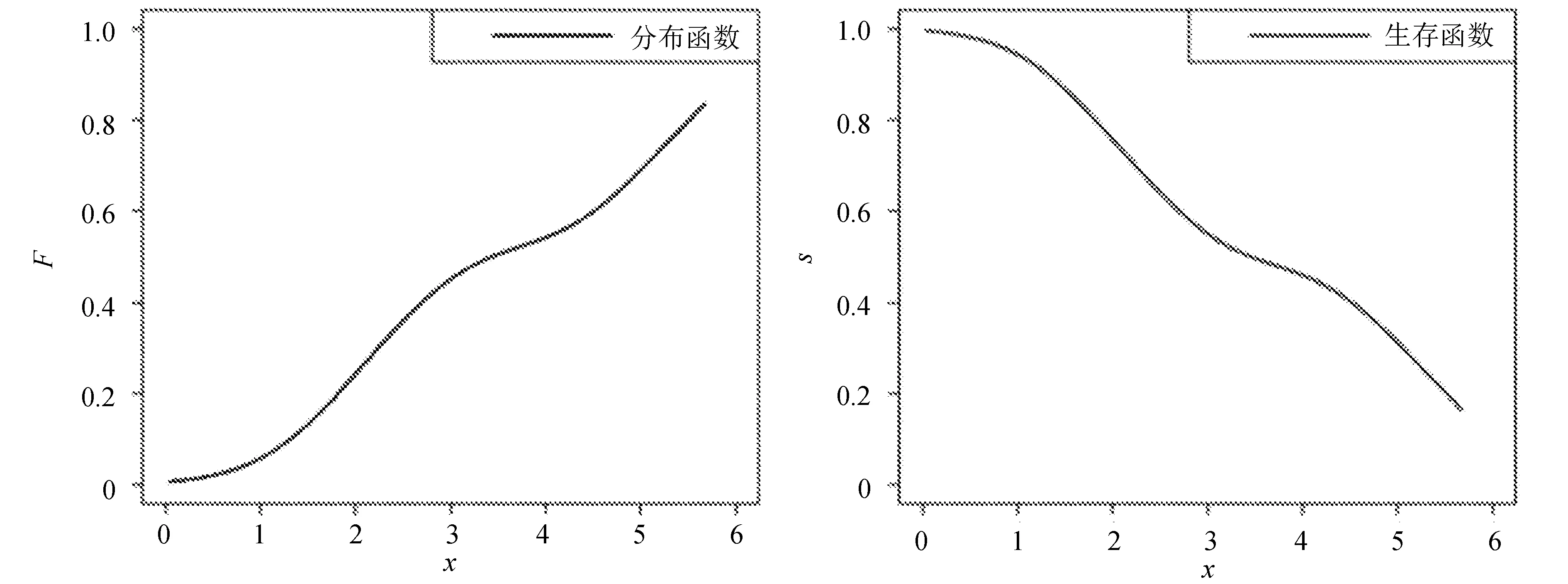
(a) OLLMON分布

图1分别展示了基于估计结果得到的OLLMON分布、MON分布与OLLN分布的分布函数与生存函数图,生存函数均呈单调递减趋势,与理论相符。对于OLLMON分布,当x=2.5左右时,风险变小,下降速度减慢,因此,临床试验中可以考虑在此处实施某些治疗方案,从而延长患者寿命,而对于MON分布和OLLN分布,可以分别在x=3.0和x=3.5左右时实施某些治疗方案。

4 结 语

OLLMON分布是一个新的扩展生存分布,与正态分布、OLLN分布、MON分布相比更为灵活。文中针对右删失数据,构建了基于OLLMON分布的参数模型,并使用极大似然方法给出感兴趣参数的估计。为验证所提模型及方法的有效性,进行了大量数值模拟研究,结果表明,参数估计效果较好。最后对NCCTG肺癌数据集进行实例数据分析,给出估计值及相应的标准差和95%置信区间,结果表明,OLLMON分布具有良好的应用性和有效性。

文中还存在很多方面的扩展研究,首先,仅讨论了右删失数据下OLLMON分布的参数估计,在之后的研究中,可将此分布拓展到其他删失机制下;其次,在文中分布的基础上,还可以进行更多拓展,如引入协变量或转化为半参数分布模型等;最后,对于参数估计方法的选择也可以进一步研究。