一种求解度约束最小生成树问题的混合整数线性规划方法∗

李中兴 卢 操 梁海镇

（华南理工大学电力学院 广州 510640）

1 引言

最小生成树问题在组合优化中是一个比较经典的问题，在拓扑设计和最短路连接等方面有广泛的应用。在工程实际应用中，生成树顶点的度往往需要满足某些约束条件。这种顶点带有度约束的最小生成树问题称为度约束最小生成树问题。

度约束最小生成树（Degree-constrained Minimum Spanning Tree，DCMST）问题的最早由Narula［1］提出，是组合优化中一个有比较重要意义和应用价值的问题［2］。目前已在通信网络、电力线网络、计算机网络以及大规模集成电路得到广泛应用［3］。

一直以来，不少学者对度约束问题进行研究。主要用贪婪启发式算法［4~5］和智能算法［6~7，12~13］求解。文献［4］在不违反度约束的前提下，提出一种由贪心算法思想而来的启发式近似算法，通过找距离当前生成树最近的顶点加入当前生成树，直到遍历所有节点。但近似算法并不能得到唯一解。文献［5］提出分支限界算法，通过求解最小生成树的方法得到初始生成树，再通过断开超过度约束的最大边，按照一定规则在某些节点连接边。该方法为一类精确的启发式算法，但复杂度高。

文献［6］通过蚁群算法求解度约束最小生成树问题，如果求解过程时没有充分考虑度约束的限制条件，经常会得不到可行解。日本学者ZHOU 和GEN 利用Prufer 编码方式对生成树进行编码［7］，并采用遗传算法求解度约束最小生成树，该研究是该问题下的一个重要突破，但编码方式容易导致不可行解产生，求解时间长，结果为局部最优解。

目前鲜有文献用线性化的思想去求解DCMST问题。文献［8］在已有的电力网络中，提出一种线性求解电力系统可靠性的方法，该思想对求解度约束最小生成树问题提供了很好的思路。

鉴于此，区别于传统DCMST 问题的求解方法，提出一种包含二进制变量与整型变量的混合整数线 性 规 划（Mixed-integer Linear Programming，MILP）模型，并对不同节点系统进行比较深入的研究。

2 度约束最小生成树问题描述

2.1 生成树描述

对于G=（V，E）的无向连通图，V=｛v1，v2，…vn｝是节点的集合，n 为节点总数。E=｛e1，e2，…，enp｝是网络G 的边集合，np 为边的总数。满足np=n-1，没有孤立节点时网络连通图为一棵生成树。如图1 所示，7节点系统有6条边，没有孤立节点。

对于含有n 个节点的生成树，生成树的总个数有T=nn-2种［11］，n=10 时已经有108种不同的连接方式，最小生成树问题（Minimum Spanning Tree，MST）求解就是在T 中寻找一棵树，使得对应边的权重wij之和有最小值，目前常用prim［2］算法和kruskal［14］算法求解。

2.2 度约束最小生成树的一般数学模型

度约束最小生成树为在生成树的基础上，对于指定的节点vi，令与vi节点所连接的边的数量为k，即d（vi）=k，则称此时的网络G 为关于节点vi的k 度生成树，含度约束最小生成树即在所有vi的k 度生成树中找到一颗使得边的权重wij之和为最小的生成树，那么，DCMST的数学模型可以用下式描述［3］：

式中，wij=wji，wii=+∞（i，j=1，2，3，…，n）。|S|为集合S中所含图G 的节点数。约束（2a）为节点度约束，约束（2b）和约束（2c）保证所得为一棵生成树。

3 求解度约束最小生成树问题的线性模型

3.1 相关知识

3.1.1 邻接矩阵

1）邻接矩阵A

邻接矩阵是表示顶点之间连接关系的矩阵。对于n 节点的无向连通图，其网络的邻接矩阵是一个对称的n 阶方阵An×n：记aij为邻接矩阵A 的元素（即节点i与节点j的连接关系），则aij=aji=1，aii=0，如式（3）所示。由于邻接矩阵为一个对称矩阵，一般而言，仅需要存储上三角元素或者下三角元素的数据即可。本文选取上三角矩阵作为数据分析，则上三角总元素个数为n（n-1）/2个，如式（4）所示。

2）上三角存储矩阵Z

对邻接矩阵A 的上三角矩阵按照从左到右，从上到下排列，得到一个上三角存储矩阵Z1×K。以5阶邻接矩阵为例，上三角元素如图2 所示，则产生的Z 矩阵为式（5）。同理对应的上三角权值存储矩阵W1×K，如式（6）所示。

图2 邻接矩阵上三角元素说明

3.1.2 关联矩阵B

生成树连通图G 有n个节点，K 条可选支路，当给每条支路规定了正方向后，则<节点—支路>的关联矩阵Bn×K的元素bik的元素定义为下式［9］，按照关联矩阵的定义，第k列元素总和为0。

由3.1.1 节可知，邻接矩阵中每一个元素aij都能生成一条边，每一条边都有对应的上三角存储矩阵Z1×K矩阵元素zk。则对于矩阵元素zk，k 与i，j的关系一一对应，如式（8）所示。

在本研究中，规定当i的发点为i，收点为j，与其一一对应的上三角存储矩阵元素为zk，对应编号k，则关联矩阵B 第k 列元素确定为下式。

3.2 度约束最小生成树问题线性化

3.2.1 度约束的线性化

节点度约束可以表示为某些节点出线度不超过某个最大值，或者不低于某个最小值。为了更好地描述这个约束，可以从邻接矩阵的上三角矩阵进行分析。还是以5阶方阵作为例子，如图3所示。

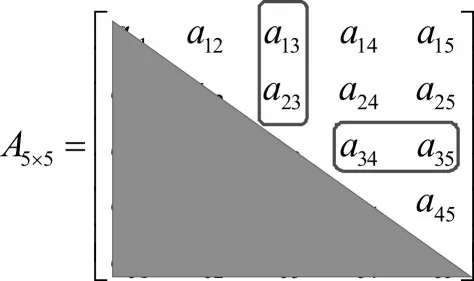
图3 节点3的待选边在邻接矩阵的位置

以节点3的出线度为例，对于节点3，其在邻接矩阵中的相关元素为｛a13，a23，a34，a35｝，由于上三角总元素数量为5*4/2=10 个。k 的计数方式从左往右，从上到下，则节点3 相关元素序号集为V3=｛2，5，8，9｝。

拓展到其他节点m，对于n 节点的无向连接图，当n 确定，Vm的序列也确定，Vm（m=1，2，3，4，5）序列下式所示：

Vm序列可以事先求出，故能快速求解度约束问题。度约束的约束方程如式（11）。

其中zk为上三角存储矩阵元素，Vm为节点m 的元素序号集。

为了方便后续的求解，本文将zk拆分为σk，σˉk，后两个变量为支路k 的正向潮流标志和反向潮流标志，为0-1变量，关系式满足：

由于zk为0-1 变量，则σk，不能同时为1，即支路k 只能允许出现正向潮流或者反向潮流。经过转换，度约束的方程可以替换为式（13）：

3.2.2 避免环产生的线性约束

传统方法中避免环路的约束，如式（2b）所示，一般避免环的产生约束条件为任意节点（2 个及以上）的连接线路满足一棵生成树。线性模型中采用直流潮流中功率平衡的方法去避免环路问题。基本思路如下。

随机挑选一个节点作为电源节点，设置其输出功率为n-1 个单位功率（p.u.），其他n-1 个节点的负荷都为1 个单位功率。则对于每个节点，都需要满足节点的功率平衡方程。

1）对于负荷节点的功率平衡约束方程

约束（14）为节点i 的功率平衡约束方程。其中，gk为支路k 的正向功率，为支路k 的反向功率，两者都大于0 的整数。Di为节点i 的功率值，本文假定都取1 个单位功率。Bik为关联矩阵元素，L为负荷节点。

约束（15）为支路k的流过的最大功率值。

约束（16），约束（17）为保证同一条线路只出现正向潮流或者反向潮流，M为一个很大的整数。

约束（18）为总出线度约束，保证生成的网络为一棵生成树。

2）电源节点功率平衡约束方程

式中，Gi为电源节点i的功率值，本文假定电源节点取n-1 个单位功率，T 为电源节点。其他相关约束参考负荷节点的约束。

3）线性约束图例

线性约束方法的思想为当有部分节点产生环路时，该部分节点的负荷得不到供应，即不满足约束条件。

如上图所示，当节点2 为电源节点时，图4（a）每一个节点的负荷都得到供应，而图4（b）因为出现了环，每个节点的功率平衡方程都不满足，这种网络满足不了约束（14）和约束（20），从而解决了避免出现环的问题。

图4 产生环路情况示意图

3.3 混合整数线性模型

1）最小生成树的线性模型

综上所述，不考虑度约束下的整数规划模型满足下式

式中，Wk为第k条支路的边长。

2）度约束最小生成树线性模型

增加约束（13），MST 线性模型变为DCMST 线性模型。

对比式（22）与式（24），DCMST 模型比MST 模型仅增加了约束式（13），说明该线性模型对求解生成树问题具有通用性。

3.4 模型求解

研究的线性模型基于CPLEX平台，调用yamilp求解器求解。CPLEX 是一个解决线性规划问题，二次规划问题以及混合整数规划问题的求解器平台，可以处理成千上万的变量及约束问题。对一定节点规模的DCMST问题有很好的求解效率。

4 算例分析

4.1 数值试验1［6］

连通图G 的节点个数n=8 个，度约束b=［1，3，3，1，1，3，1，3］，对应的权值矩阵如下：

求解结果如表1。

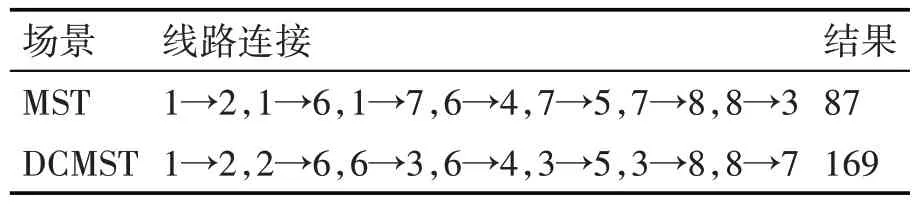
表1 数值试验1的求解结果

DCMST 问题的求解的最优值为169，与现在公布的最优解相同。此外，由于线性模型只有唯一解，可证明，该解为当前实例的最优解。

4.2 数值试验2［4］

连通图G 的节点个数n=9，度约束b=［2，2，2，2，2，2，2，1，1］，对应的权值矩阵如下。

求解结果如表2。

表2 数值试验2的求解结果

度约束的求解的最优值为40，与现在公布的最优解相同。同样可证明，该解为当前实例的最优解。

4.3 旅行商问题

旅行商问题，即TSP 问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n 个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

该问题的约束条件需要将式（13）和式（18）作一定修改得到，式（13）修改为每个节点的出线度都等于2，式（18）修改为系统总出线度等于n，如下所示。

采用旅行商问题eil51［10］中的数据进行实例仿真，仿真结果如表3。

表3 eil51系统仿真结果

目前公布的最优数值426，是基于对城市间距离四舍五入取整得到的，本文将从进行取整和不进行取整求解出最优的规划结果。如表3所示。

标粗黑体的部分为两者不同的部分，两者具体连接图5、6所示。

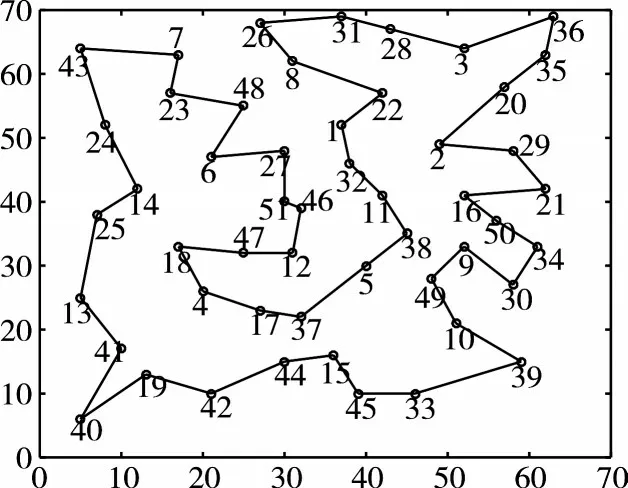
图5 进行取整后的最优连接图

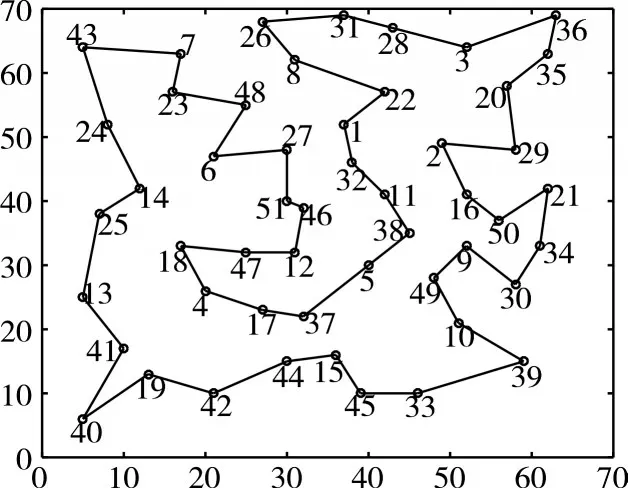
图6 不进行取整后的最优连接图

同样可以证明，对城市距离四舍五入取整后的最优解为426，不进行取整的最优解为428.87。

5 结语

本文提出了一种求解度约束最小生成树问题的混合整数线性规划模型，模型适合MST 问题、DCMST问题、TSP问题以及其他有约束的生成树距离问题，具有一定的通用性。